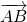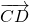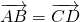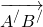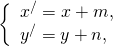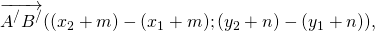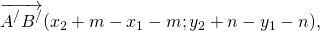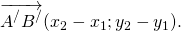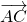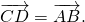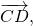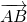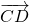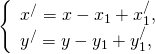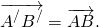Как узнать равны ли векторы по координатам (8 видео)

Равные вектора

То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:

a = b , если a ↑↑ b и | a | = | b |.

Как узнать равны ли векторы по координатам

рис. 1

Содержание

Примеры задач на равенство векторов
Примеры плоских задач на равенство векторов
Примеры пространственных задач на равенство векторов
Векторы на плоскости и в пространстве — основные определения
Определение вектора
Нулевой вектор
Длина вектора
Коллинеарность векторов
Направление векторов
Равные и противоположные векторы
Углы между векторами
Равные векторы
🔥 Видео

Видео:Координаты вектора. 9 класс.Скачать

Примеры задач на равенство векторов

Примеры плоских задач на равенство векторов

a = b — так как их координаты равны,
a ≠ c — так как их координаты не равны,
b ≠ c — так как их координаты не равны.

Проверим равенство компонентов векторов
a_x = b_x = 1
a_y = b_y => 8 = 2 n => n = 8/2 = 4

Ответ: при n = 4 вектора a и b равны.

Примеры пространственных задач на равенство векторов

a = c — так как их координаты равны,
a ≠ b — так как их координаты не равны,
b ≠ c — так как их координаты не равны.

Проверим равенство компонентов векторов
a_x = b_x = 1
a_y = b_y = 2
a_z = b_z => 4 = 2 n => n = 4/2 = 2

Ответ: при n = 2 вектора a и b равны.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Векторы на плоскости и в пространстве — основные определения

Видео:9 класс, 2 урок, Координаты вектораСкачать

Определение вектора

В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.

Для начала дадим определение:

Вектор – это направленный отрезок прямой.

Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.

В математике для обозначения вектора обычно используют строчные латинские буквы, однако над вектором всегда ставится небольшая стрелочка, например a → . Если известны граничные точки вектора – его начало и конец, к примеру A и B , то вектор обозначается так A B → .

Видео:Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Нулевой вектор

Под нулевым вектором 0 → будем понимать любую точку плоскости или пространства.

Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.

Видео:Длина вектора через координаты. 9 класс.Скачать

Длина вектора

Под длиной вектора A B → понимается число, большее либо равное 0, и равное длине отрезка АВ.

Длину вектора A B → принято обозначать так A B → .

Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин «длина вектора». Очевидно, что длина нулевого вектора принимает значение ноль.

Видео:Вектора с равными координатамиСкачать

Коллинеарность векторов

Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.

Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.

Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.

Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.

Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

Направление векторов

Сонаправленными векторами называют два коллинеарных вектора a → и b → , у которых направления совпадают, такие векторы обозначаются так a → ↑ ↑ b → .

Противоположно направленными векторами называются два коллинеарных вектора a → и b → , у которых направления не совпадают, т.е. являются противоположными, такие векторы обозначаются следующим образом a → ↑ ↓ b → .

Считается, что нулевой вектор является сонаправленым к любым другим векторам.

Видео:11 класс, 3 урок, Связь между координатами векторов и координатами точекСкачать

Равные и противоположные векторы

Равными называются сонаправленные вектора, у которых длины равны.

Противопожными называются противоположно направленные вектора, у которых их длины равны.

Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам. Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.

Пусть заданы два произвольных вектора на плоскости или в пространстве a → и b → . Отложим от некоторой точки O плоскости или пространства векторы O A → = a → и O B → = b → . Лучи OA и OB образуют угол ∠ A O B = φ .

Видео:Коллинеарность векторовСкачать

Углы между векторами

Угол φ = ∠ A O B называется углом между векторами a → = O A → и b → = O B → .

Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.

Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π 2 радиан).

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Равные векторы

В различных школьных учебниках определение равных векторов даётся по-разному.

В классическом учебнике Погорелова А. В. понятие равных векторов вводится с помощью параллельного переноса.

Два вектора называются равными, если они совмещаются параллельным переносом.

(то есть существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого).

Например, изображенные на рисунке

Равенство векторов обозначают так:

(Свойства равных векторов)

1) Равные векторы сонаправлены и имеют равные длины.

2) Равные векторы имеют равные координаты.

3) От любой точки можно отложить вектор, равный данному, и притом только один.

1) 1-е свойство вытекает непосредственно из определения равных векторов и свойств параллельного переноса.

2) Пусть дан вектор

с началом в точке A(x₁; y₁) и концом в точке B(x₂; y₂).

По определению равных векторов, вектор

равный данному, получен из

Если этот параллельный перенос задан формулами

Найдём координаты каждого из векторов:

То есть координаты равных векторов

Что и требовалось доказать.

Таким образом, координаты задают длину и направление вектора, но не фиксируют его.

3) Пусть даны вектор

и точка C.
Существует и притом единственный параллельный перенос, при котором точка A переходит в точку C — параллельный перенос на вектор

При таком параллельном переносе вектор

переходит в вектор

По определению равных векторов,

Что и требовалось доказать.

На практике, если требуется отложить от некоторой точки вектор, равный данному, удобно это делать с помощью параллелограмма (если точка, от которой откладывается вектор, не лежит на прямой, содержащей этот вектор).

Например,

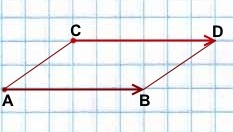
отложенный от точки C, равен вектору

(Признаки равенства векторов)

1) Если векторы сонаправлены и имеют одинаковые длины, то они равны.

2) Если у векторов соответствующие координаты равны, то векторы равны.

1) Пусть векторы

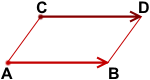
сонаправлены и имеют одинаковые длины.

Параллельный перенос, который переводит точку A в точку C, совмещает луч CD с лучом AB (поскольку векторы одинаково направлены). А так как длины отрезков CD и AB равны, то точка D при этом совместится с точкой B. Таким образом, этот параллельный перенос вектор