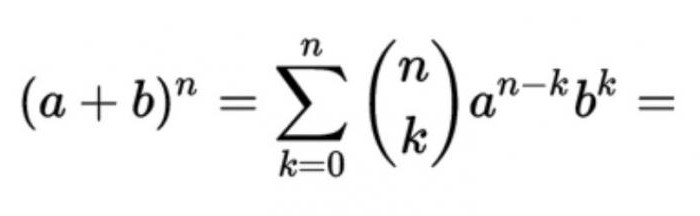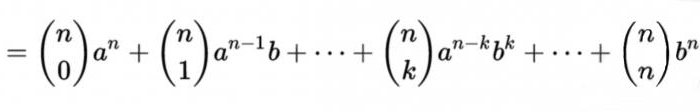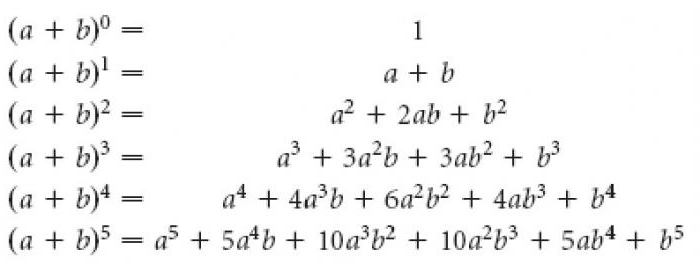- Основная формула
- История открытия
- Отличительные черты
- Общие свойства
- Секреты треугольника
- Полномочия двойки
- Силы одиннадцати
- Совершенные квадраты
- Комбинаторные варианты
- Действия с биномами
- Треугольник Паскаля. Свойства треугольника Паскаля
- Несколько слов о гении
- Арифметический треугольник Паскаля
- Немного истории
- Описание
- Основные свойства
- Связь с биномом Ньютона
- Математические чудеса
- Треугольник Серпинского
- Несколько интересных задач
- Треугольник Паскаля в комбинаторных задачах
- Скачать:
- Предварительный просмотр:
Видео:9.3 Комбинаторное доказательство - пример - треугольник паскаляСкачать

Основная формула
Строки треугольника обычно нумеруются, начиная со строки n = 0 в верхней части. Записи в каждой строке целочисленные и нумеруются слева, начиная с k = 0, обычно располагаются в шахматном порядке относительно чисел в соседних строчках. Построить фигуру можно следующим образом:
- В центре верхней части листа ставится цифра «1».
- В следующем ряду — две единицы слева и справа от центра (получается треугольная форма).
- В каждой последующей строке ряд будет начинаться и заканчиваться числом «1». Внутренние члены вычисляются путём суммирования двух цифр над ним.
Запись в n строке и k столбце паскалевской фигуры обозначается (n k). Например, уникальная ненулевая запись в самой верхней строке (0 0) = 1. С помощью этого конструкция предыдущего абзаца может быть записана следующим образом, образуя формулу треугольника Паскаля (n k) = (n — 1 k-1) + (n — 1 k), для любого неотрицательного целого числа n и любого целого числа k от 0 до n включительно. Трёхмерная версия называется пирамидой или тетраэдром, а общие — симплексами.
Видео:Треугольник ПаскаляСкачать

История открытия
Паскаль ввёл в действие многие ранее недостаточно проверенные способы использования чисел треугольника, и он подробно описал их в, пожалуй, самом раннем из известных математических трактатов, специально посвящённых этому вопросу, в труде об арифметике Traité du triangle (1665). За столетия до того обсуждение чисел возникло в контексте индийских исследований комбинаторики и биномиальных чисел, а у греков были работы по «фигурным числам».
Из более поздних источников видно, что биномиальные коэффициенты и аддитивная формула для их генерации были известны ещё до II века до нашей эры по работам Пингала. К сожалению, бо́льшая часть трудов была утеряна. Варахамихира около 505 года дал чёткое описание аддитивной формулы, а более подробное объяснение того же правила было дано Халаюдхой (около 975 года). Он также объяснил неясные ссылки на Меру-прастаара, лестницы у горы Меру, дав первое сохранившееся определение расположению этих чисел, представленных в виде треугольника.
Примерно в 850 году джайнский математик Махавира вывел другую формулу для биномиальных коэффициентов, используя умножение, эквивалентное современной формуле. В 1068 году Бхаттотпала во время своей исследовательской деятельности вычислил четыре столбца первых шестнадцати строк. Он был первым признанным математиком, который уравнял аддитивные и мультипликативные формулы для этих чисел.
Примерно в то же время персидский учёный Аль-Караджи (953–1029) написал книгу (на данный момент утраченную), в которой содержалось первое описание треугольника Паскаля. Позднее работа была переписана персидским поэтом, астрономом и математиком Омаром Хайямом (1048–1131). Таким образом, в Иране фигура упоминается как треугольник Хайяма.
Известно несколько теорем, связанных с этой темой, включая биномы. Хайям использовал метод нахождения n-x корней, основанный на биномиальном разложении и, следовательно, на одноимённых коэффициентах. Треугольник был известен в Китае в начале XI века благодаря работе китайского математика Цзя Сианя (1010–1070). В XIII веке Ян Хуэй (1238–1298) представил этот способ, и поэтому в Китае он до сих пор называется треугольником Ян Хуэя.
На западе биномиальные коэффициенты были рассчитаны Жерсонидом в начале XIV века, он использовал мультипликативную формулу. Петрус Апиан (1495–1552) опубликовал полный треугольник на обложке своей книги примерно в 1527 году. Это была первая печатная версия фигуры в Европе. Майкл Стифель представил эту тему как таблицу фигурных тел в 1544 году.
В Италии паскалевский треугольник зовут другим именем, в честь итальянского алгебраиста Никколо Фонтана Тарталья (1500–1577). Вообще, современное имя фигура приобрела благодаря Пьеру Раймонду до Монтрмору (1708), который назвал треугольник «Таблица Паскаля для сочетаний» (дословно: Таблица мистера Паскаля для комбинаций) и Абрахамом Муавром (1730).
Видео:Числа сочетаний. Треугольник Паскаля | Ботай со мной #059 | Борис Трушин |Скачать

Отличительные черты
Треугольник Паскаля и его свойства — тема довольно обширная. Главное, в нём содержится множество моделей чисел. Обзор следует начать с простого — ряды:
- Сумма элементов одной строки в два раза больше суммы строки, предшествующей ей. Например, строка 0 (самая верхняя) имеет значение 1, строчка 1–2, а 2 имеет значение 4 и т. д. Это потому что каждый элемент в строке производит два элемента в следующем ряду: один слева и один справа. Сумма элементов строки n равна 2 n .
- Принимая произведение элементов в каждой строке, последовательность продуктов можно связать с основанием натурального логарифма.
- В треугольнике Паскаля через бесконечный ряд Нилаканты можно найти число Пи.
- Значение строки, если каждая запись считается десятичным знаком (имеется в виду, что числа больше 9 переносятся соответственно), является степенью 11 (11 n для строки n). Таким образом, в строке 2 ⟨1, 2, 1⟩ становится 11 2 , равно как ⟨1, 5, 10, 10, 5, 1⟩ в строке пять становится (после переноса) 161, 051, что составляет 11 5 . Это свойство объясняется установкой x = 10 в биномиальном разложении (x + 1) n и корректировкой значений в десятичной системе.
- Некоторые числа в треугольнике Паскаля соотносятся с числами в треугольнике Лозанича.
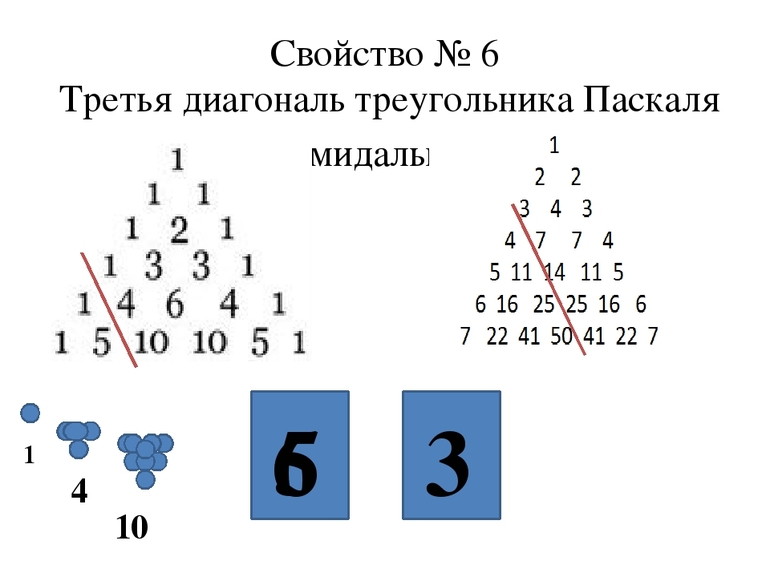
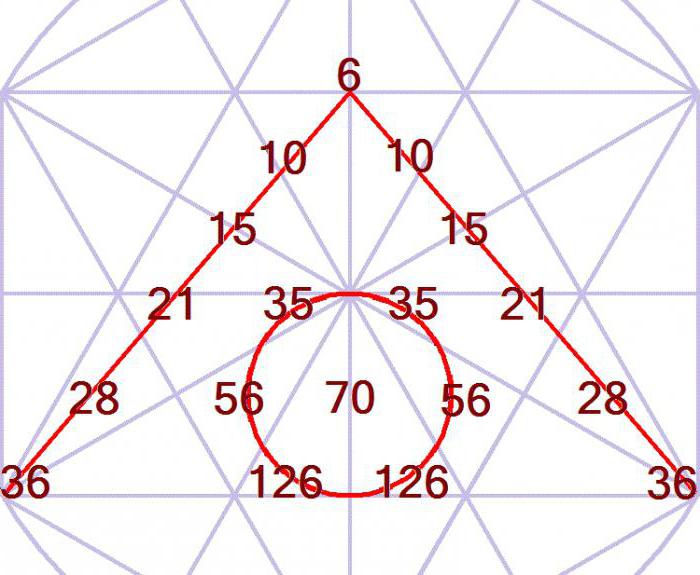
- Сумма квадратов элементов строки n равна среднему элементу строки 2 n. Например, 1 2 + 4 2 + 6 2 + 4 2 + 1 2 = 70.
- В любой строчке n, где n является чётным, средний член за вычетом члена в двух точках слева равен каталонскому числу (n / 2 + 1).
- В строчке р, где р представляет собой простое число, все члены в этой строке, за исключением 1s, являются кратными р.
- Чётность. Для измерения нечётных терминов в строке n необходимо преобразовать n в двоичную форму. Пусть x будет числом 1s в двоичном представлении. Тогда количество нечётных членов будет 2 х . Эти числа являются значениями в последовательности Гулда.
- Каждая запись в строке 2 n -1, n ≥ 0, является нечётной.
- Полярность. Когда элементы строки треугольника Паскаля складываются и вычитаются вместе последовательно, каждая строка со средним числом, означающим строки с нечётным числом целых чисел, даёт 0 в качестве результата.
Диагонали треугольника содержат фигурные числа симплексов. Например:
- Идущие вдоль левого и правого краёв диагонали содержат только 1.
- Рядом с рёбрами диагонали содержат натуральные числа по порядку.
- Двигаясь внутрь, следующая пара содержит треугольные числа по порядку.
- Следующая пара — тетраэдрические, а следующая пара — числа пятиугольника.
Существуют простые алгоритмы для вычисления всех элементов в строке или диагонали без вычисления других элементов или факториалов.
Видео:Зачем нужен треугольник Паскаля (спойлер: для формул сокращённого умножения)Скачать

Общие свойства
Образец, полученный путём раскраски только нечётных чисел, очень похож на фрактал, называемый треугольником Серпинского. Это сходство становится всё более точным, так как рассматривается больше строк в пределе, когда число рядов приближается к бесконечности, получающийся в результате шаблон представляет собой фигуру, предполагающую фиксированный периметр. В целом числа могут быть окрашены по-разному в зависимости от того, являются ли они кратными 3, 4 и т. д.
В треугольной части сетки количество кратчайших путей от заданного до верхнего угла треугольника является соответствующей записью в паскалевском треугольнике. На треугольной игровой доске Плинко это распределение должно давать вероятности выигрыша различных призов. Если строки треугольника выровнены по левому краю, диагональные полосы суммируются с числами Фибоначчи.
Благодаря простому построению факториалами можно дать очень простое представление фигуры Паскаля в терминах экспоненциальной матрицы: треугольник — это экспонента матрицы, которая имеет последовательность 1, 2, 3, 4… на её субдиагонали, а все другие точки — 0.
Количество элементов симплексов фигуры можно использовать в качестве справочной таблицы для количества элементов (рёбра и углы) в многогранниках (треугольник, тетраэдр, квадрат и куб).
Шаблон, созданный элементарным клеточным автоматом с использованием правила 60, является в точности паскалевским треугольником с биномиальными коэффициентами, приведёнными по модулю 2. Правило 102 также создаёт этот шаблон, когда завершающие нули опущены. Правило 90 создаёт тот же шаблон, но с пустой ячейкой, разделяющей каждую запись в строках. Фигура может быть расширена до отрицательных номеров строк.
Видео:Бином Ньютона: формула, доказательство и Треугольник ПаскаляСкачать

Секреты треугольника
Конечно, сейчас большинство расчётов для решения задач не в классе можно сделать с помощью онлайн-калькулятора. Как пользоваться треугольником Паскаля и для чего он нужен, обычно рассказывают в школьном курсе математики. Однако его применение может быть гораздо шире, чем принято думать.
Начать следует со скрытых последовательностей. Первые два столбца фигуры не слишком интересны — это только цифры и натуральные числа. Следующий столбец — треугольные числа. Можно думать о них, как о серии точек, необходимых для создания групп треугольников разных размеров.
Точно так же четвёртый столбец — это тетраэдрические числа или треугольные пирамидальные. Как следует из их названия, они представляют собой раскладку точек, необходимых для создания пирамид с треугольными основаниями.
Столбцы строят таким образом, чтобы описывать «симплексы», которые являются просто экстраполяциями идеи тетраэдра в произвольные измерения. Следующий столбец — это 5-симплексные числа, затем 6-симплексные числа и так далее.
Полномочия двойки
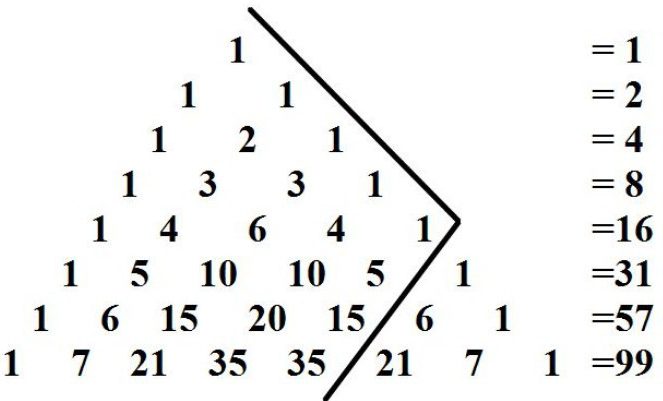
Если суммировать каждую строку, получатся степени основания 2 начиная с 2⁰ = 1. Если изобразить это в таблице, то получится следующее:
| 1 | ||||||||||||||
| 1 | + | 1 | = | 2 | ||||||||||
| 1 | + | 2 | + | 1 | = | 4 | ||||||||
| 1 | + | 3 | + | 3 | + | 1 | = | 8 | ||||||
| 1 | + | 4 | + | 6 | + | 4 | + | 1 | = | 16 | ||||
| 1 | + | 5 | + | 10 | + | 10 | + | 5 | + | 1 | = | 32 | ||
| 1 | + | 6 | + | 15 | + | 20 | + | 15 | + | 6 | + | 1 | = | 64 |
Суммирование строк показывает силы базы 2.
Силы одиннадцати
Треугольник также показывает силы основания 11. Всё, что нужно сделать, это сложить числа в каждом ряду вместе. Как показывает исследовательский опыт, этого достаточно только для первых пяти строк. Сложности начинаются, когда записи состоят из двузначных чисел. Например:
| 1 | = | 11° |
| 11 | = | 11¹ |
| 121 | = | 11² |
| 1331 | = | 11³ |
Оказывается, всё, что нужно сделать — перенести десятки на одно число слева.
Совершенные квадраты
Если утверждать, что 4² — это 6 + 10 = 16, то можно найти идеальные квадраты натуральных чисел в столбце 2, суммируя число справа с числом ниже. Например:
- 2² → 1 + 3 = 4
- 3² → 3 + 6
- 4² → 6 + 10 = 16 и так далее.
Комбинаторные варианты
Чтобы раскрыть скрытую последовательность Фибоначчи, которая на первый взгляд может отсутствовать, нужно суммировать диагонали лево-выровненного паскалевского треугольника. Первые 7 чисел в последовательности Фибоначчи: 1, 1, 2, 3, 5, 8, 13… найдены. Используя исходную ориентацию, следует заштриховать все нечётные числа, и получится изображение, похожее на знаменитый фрактальный треугольник Серпинского.
Возможно, самое интересное соотношение, найденное в треугольнике — это то, как можно использовать его для поиска комбинаторных чисел, поскольку его первые шесть строк написаны с помощью комбинаторной записи. Поэтому, если нужно рассчитать 4, стоит выбрать 2, затем максимально внимательно посмотреть на пятую строку, третью запись (поскольку счёт с нуля), и будет найден ответ.
Видео:Бином Ньютона и треугольник Паскаля | Учитель года Москвы — 2020Скачать

Действия с биномами
Например, есть бином (x + y), и стоит задача повысить его до степени, такой как 2 или 3. Обычно нужно пройти долгий процесс умножения (x + y)² = (x + y)(x + y) и т. д. Если воспользоваться треугольником, решение будет найдено гораздо быстрее. К примеру, нужно расширить (x + y)³. Поскольку следует повышать (x + y) до третьей степени, то необходимо использовать значения в четвёртом ряду фигуры Паскаля (в качестве коэффициентов расширения). Затем заполнить значения x и y. Получится следующее: 1 x³ + 3 x²y + 3 xy² + 1 y³. Степень каждого члена соответствует степени, до которой возводится (x + y).
В виде более удобной формулы этот процесс представлен в теореме бинома. Как известно, всё лучше разбирать на примерах. Итак — (2x – 3)³. Пусть x будет первым слагаемым, а y — вторым. Тогда x = 2x, y = –3, n = 3 и k — целые числа от 0 до n = 3, в этом случае k = . Следует внести эти значения в формулу. Затем заполнить значения для k, которое имеет 4 разные версии, их нужно сложить вместе. Лучше упростить условия с показателями от нуля до единицы.
Как известно, комбинаторные числа взяты из треугольника, поэтому можно просто найти четвёртую строку и подставить в значения 1, 3, 3, 1 соответственно, используя соответствующие цифры Паскаля 1, 3, 3, 1. Последнее — необходимо завершить умножение и упрощение, в итоге должно получиться: 8 x³ — 36 x² + 54x — 27. С помощью этой теоремы можно расширить любой бином до любой степени, не тратя время на умножение.
Биномиальное распределение описывает распределение вероятностей на основе экспериментов, которые можно разделить на группы с двумя возможными исходами. Самый классический пример этого — бросание монеты. Например, есть задача выбросить «решку» — успех с вероятностью p. Тогда выпадение «орла» является случаем «неудачи» и имеет вероятность дополнения 1 – p.
Если спроектировать этот эксперимент с тремя испытаниями, с условием, что нужно узнать вероятность выпадения «решки», можно использовать функцию вероятности массы (pmf) для биномиального распределения, где n — это количество испытаний, а k — это число успехов. Предполагаемая вероятность удачи — 0,5 (р = 0,5). Самое время обратиться к треугольнику, используя комбинаторные числа: 1, 3, 3, 1. Вероятность получить ноль или три «решки» составляет 12,5%, в то время как переворот монеты один или два раза на сторону «орла» — 37,5%. Вот так математика может применяться в жизни.
Видео:202 Комбинаторное доказательство малой теоремы Ферма, треугольник Паскаля и бином НьютонаСкачать

Треугольник Паскаля. Свойства треугольника Паскаля
Прогресс человечества во многом связан с открытиями, сделанными гениями. Одним из них является Блез Паскаль. Его творческая биография еще раз подтверждает истинность выражения Лиона Фейхтвангера «Талантливый человек, талантлив во всем». Все научные достижения этого великого ученого трудно перечесть. К их числу относится одно из самых элегантных изобретений в мире математики — треугольник Паскаля.
Видео:Числа Фибоначчи и треугольник ПаскаляСкачать

Несколько слов о гении
Блез Паскаль по современным меркам умер рано, в возрасте 39 лет. Однако за свою короткую жизнь он проявил себя как выдающийся физик, математик, философ и писатель. Благодарные потомки назвали в его честь единицу давления и популярный язык программирования Pascal. Он уже почти 60 лет используется для обучения написания различных кодов. Например, с его помощью каждый школьник может написать программу для вычисления площади треугольника на «Паскале», а также исследовать свойства схемы, о которой речь пойдет ниже.
Деятельность этого ученого с экстраординарным мышлением охватывает самые разные области науки. В частности, Блез Паскаль является одним из основателей гидростатики математического анализа, некоторых направлений геометрии и теории вероятностей. Кроме того, он:
- создал механический калькулятор, известный под названием Паскалева колеса;
- представил экспериментальное доказательство того, что воздух обладает упругостью и имеет вес;
- установил, что барометр можно использовать для предсказания погоды;
- изобрел тачку;
- придумал омнибус — конные экипажи с фиксированными маршрутами, ставшие впоследствии первым видом регулярного общественного транспорта и пр.
Видео:Треугольник ПаскаляСкачать

Арифметический треугольник Паскаля
Как уже было сказано, этот великий французский ученый внес огромный вклад в математическую науку. Одним из его безусловных научных шедевров является «Трактат об арифметическом треугольнике», который состоит из биномиальных коэффициентов, расставленных в определенном порядке. Свойства этой схемы поражают своим разнообразием, а сама она подтверждает пословицу «Все гениальное — просто!».
Видео:Несколько красивых свойств треугольника ПаскаляСкачать
Немного истории
Справедливости ради нужно сказать, что на самом деле треугольник Паскаля был известен в Европе еще в начале 16 века. В частности, его изображение можно увидеть на обложке учебника арифметики известного астронома Петра Апиана из Ингольтштадского университета. Похожий треугольник представлен и в качестве иллюстрации в книге китайского математика Ян Хуэй, изданной в 1303 году. О его свойствах было известно также и замечательному персидскому поэту и философу Омару Хайяму еще в начале 12 века. Причем считается, что он познакомился с ним из трактатов арабских и индийских ученых, написанных ранее.
Видео:Математические секреты треугольника ПаскаляСкачать

Описание
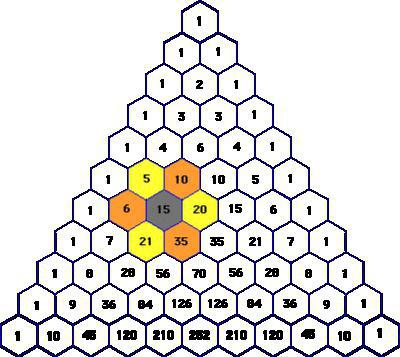
Прежде чем исследовать интереснейшие свойства треугольника Паскаля, прекрасного в своем совершенстве и простоте, стоит узнать, что он из себя представляет.
Говоря научным языком, эта числовая схема — бесконечная таблица треугольной формы, образованная из биномиальных коэффициентов, расположенных в определенном порядке. В его вершине и по бокам находятся цифры 1. Остальные позиции занимают числа, равные сумме двух чисел, расположенных над ними рядом выше. При этом все строки треугольника Паскаля симметричны относительно его вертикальной оси.
Видео:БИНОМ Ньютона | треугольник ПаскаляСкачать

Основные свойства
Треугольник Паскаля поражает своим совершенством. Для любой строки под номером n (n = 0, 1, 2…) верно:
- первое и последнее числа — 1;
- второе и предпоследнее — n;
- третье число равно треугольному числу (количеству кружков, которые можно расставить в виде равностороннего треугольника, т. е. 1, 3, 6, 10): Tn-1 = n (n — 1) / 2.
- четвертое число является тетраэдрическим, т. е. представляет собой пирамиду с треугольником в основании.
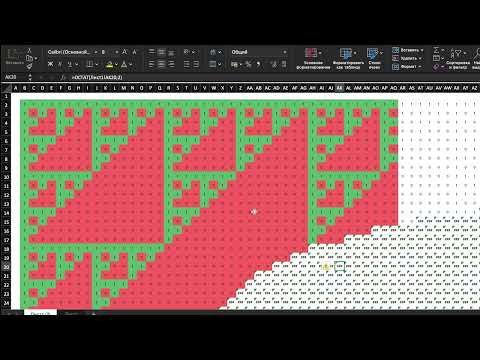
Кроме того, сравнительно недавно, в 1972 году, было установлено еще одно свойство треугольника Паскаля. Для того чтобы его обнаружить, нужно записать элементы этой схемы в виде таблицы со сдвигом строк на 2 позиции. Затем отмечают числа, делящиеся на номер строки. Оказывается, что номер столбца, в котором выделены все числа, является простым числом.
Тот же трюк можно осуществить и по-другому. Для этого в треугольнике Паскаля заменяют числа на остатки от их деления на номер строки в таблице. Затем располагают строки в полученном треугольнике так, чтобы следующая из них начиналась правее на 2 колонки от первого элемента предыдущей. Тогда столбцы, имеющие номера, являющиеся простыми числами, будут состоять только из нулей, а в тех, у которых они составные, будет присутствовать хотя бы один ноль.
Видео:ТРЕУГОЛЬНИК ПАСКАЛЯ 😊 ЧАСТЬ I #shorts #математика #егэ #задачи #задачаналогику #егэ2022 #огэ2022Скачать

Связь с биномом Ньютона
Как известно, так называется формула для разложения на слагаемые целой неотрицательной степени суммы двух переменных, которая имеет вид:
Присутствующие в них коэффициенты равны Cn m = n! / (m! (n — m)!), где m, представляет собой порядковый номер числа в строке n треугольника Паскаля. Иными словами, имея под рукой эту таблицу, можно легко возводить в степень любые числа, предварительно разложив их на два слагаемых.
Таким образом, треугольник Паскаля и бином Ньютона взаимосвязаны самым тесным образом.
Видео:Комбинаторика 05 Треугольник ПаскаляСкачать

Математические чудеса
При внимательном изучении треугольника Паскаля можно обнаружить, что:
- сумма всех чисел в строке с порядковым номером n (отсчет ведется с 0) равна 2 n ;
- если строки выровнять по левому краю, то суммы чисел, которые расположены вдоль диагоналей треугольника Паскаля, идущих снизу вверх и слева направо, равны числам Фибоначчи;
- первая «диагональ» состоит из натуральных чисел, идущих по порядку;
- любой элемент из треугольника Паскаля, уменьшенный на единицу, равен сумме всех чисел, расположенных внутри параллелограмма, который ограничен левыми и правыми диагоналями, пересекающимися на этом числе;
- в каждой строке схемы сумма чисел на четных местах равна сумме элементов на нечетных местах.
Видео:Основы комбинаторикиСкачать

Треугольник Серпинского
Такая интересная математическая схема, достаточно перспективная с точки зрения решения сложных задач, получается, если раскрасить четные числа Паскалевого изображения в один цвет, а нечетные — в другой.
Треугольник Серпинского можно выстроить и другим образом:
- в закрашенной схеме Паскаля перекрашивают в другой цвет серединный треугольник, который образован путем соединения середин сторон исходного;
- точно также поступают с тремя незакрашенными, расположеными в углах;
- если процедуру продолжать бесконечно, то в итоге должна получиться двухцветная фигура.
Самое интересное свойство треугольника Серпинского — его самоподобие, так как он состоит из 3-х своих копий, которые уменьшены в 2 раза. Оно позволяет отнести эту схему к фрактальным кривым, а они, как показывают новейшие исследования лучше всего подходят для математического моделирования облаков, растений, дельт рек, да и самой Вселенной.
Видео:Сочетания в комбинаторике. Применение треугольника Паскаля.Скачать

Несколько интересных задач
Где используется треугольник Паскаля? Примеры задач, которые можно решать с его помощью, достаточно разнообразны и относятся к различным областям науки. Рассмотрим некоторые, наиболее интересные из них.
Задача 1. У некоторого большого города, обнесенного крепостной стеной, только одни входные ворота. На первом перекрестке основная дорога расходится на две. То же происходит и на любом другом. В город заходят 210 человек. На каждом из встречающихся перекрестков они делятся пополам. Сколько человек будет находить на каждом перекрестке, когда делиться будет уже невозможно. Ее ответом является 10 строка треугольника Паскаля (формула коэффициентов представлена выше), где по обе стороны от вертикальной оси расположены числа 210.
Задача 2. Имеется 7 наименований цветов. Нужно составить букет из 3 цветков. Требуется выяснить, сколькими различными способами это можно сделать. Эта задача из области комбинаторики. Для ее решения опять же используем треугольник Паскаля и получаем на 7 строке на третьей позиции (нумерация в обоих случаях с 0) число 35.
Теперь вы знаете, что изобрел великий французский философ и ученый Блез Паскаль. Его знаменитый треугольник при правильном использовании может стать настоящей палочкой-выручалочкой для решения множества задач, особенно из области комбинаторики. Кроме того, его возможно использовать для разгадывания многочисленных загадок, связанных с фракталами.
Видео:Комбинаторика 6. Треугольник Паскаля. Формула включений исключений. Часть 1Скачать

Треугольник Паскаля в комбинаторных задачах
В данной работе рассмотрены примеры решения комбинаторных задач и задач по теории вероятностей с помощью треугольника Паскаля.
Видео:Комбинаторное доказательство ( доказательство без формул, невозможное возможно)Скачать

Скачать:
| Вложение | Размер |
|---|---|
| strokach_nikita_shkola_25._treugolnik_paskalya.rar | 801.08 КБ |
Видео:Комбинаторика 3: Бином Ньютона и треугольник Паскаля.Скачать

Предварительный просмотр:
Задача 1 .В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?
В треугольнике Паскаля число, показывающее, сколькими способами можно выбрать k элементов из множества, содержащего n различных элементов, стоит на пересечении k-ой диагонали и n-ой строки.
Найду диагональ восьмую сверху и отсчитываю три числа по горизонтали. Получу число 56.
Задача 2. Из шести врачей поликлиники двух необходимо отправить на курсы повышения квалификации. Сколькими способами это можно сделать?
Найду диагональ шестую сверху и отсчитываю два числа по горизонтали. Получу число 15.
Задача 3. Сколько различных двухзначных чисел можно составить, используя цифры 1, 2, 3, 4 при условии, что ни одна цифра не повторяется?
Найду диагональ четвёртую сверху и отсчитываю два числа по горизонтали. Получу число 6. Вычислю факториал числа 2, получу 2. Искомое произведение равно 12.
Задача 4 . У ювелира есть пять изумрудов, восемь алмазов, четыре топаза. Сколькими способами он может сделать браслет, включив в него два изумруда, три алмаза и два топаза?
Два изумруда из пяти имеющихся можно выбрать 10 способами, три алмаза из восьми 56 способами, два топаза из четырёх 6 способами. Браслет можно сделать 3360 способами, т.е.
Задача 5 . В пачке находятся одинаковые по размеру 7 тетрадей в линейку и 5 в клетку. Из пачки наугад берут 3 тетради. Какова вероятность того, что все три тетради окажутся в клетку?
Решение. Сначала найдём общее число возможных исходов, т.е. сколькими способами мы можем выбрать 3 тетради из 12 тетрадей
А сколькими способами мы можем выбрать 3 тетради в клетку из имеющихся 5 тетрадей?
Вероятностью Р наступления случайного события А называется отношение m/n, где n – число всех возможных исходов эксперимента, а m – число всех благоприятных исходов: Р(А)= m/n.
По формуле нахождения вероятности получим
Задача 6 .На плоскости даны 10 прямых, причём среди них нет параллельных и через каждую точку их пересечения проходят ровно две прямые. Сколько у них точек пересечения?
Решение: ответ находится на пересечении —
На плоскости даны 14 прямых, причём четыре из них параллельны и через каждую точку их пересечения проходят ровно две прямые. Сколько у них точек пересечения?
Решение: В предыдущей задаче было 10 непараллельных прямых и они имели 45 точек пересечения. Одна из 10 непараллельных пересекает четыре параллельные в 4 точках, т.е. добавим ещё 40 точек пересечения. В ответе получим 85 точек пересечения.
Сколько нечетных трехзначных чисел (без повторения цифр в числе) можно составить из цифр 1, 2, 3,4, 5?
Всего можно составить 60 чисел. Из них у 12 чисел запись заканчивается цифрой 1, у следующих 12 чисел на 2, ещё у 12 на 3, ещё у 12 на 4, у последних 12 на 5. Исключим 24 чётных числа, запись которых оканчивается на 2 и 4. Наш ответ 36 чисел.
В сумке 10 мячей, пронумерованных от 1 до 10. Наугад вынимают 2 мяча. Какова вероятность того, что это будут мячи с номерами 7 и 3?
Вынуть 2 мяча из 10 имеющихся можно 45 способами. Вероятность нашего события 2 из 45.
На плоскости даны 11 точек, из которых никакие три не лежат на одной прямой и никакие четыре не лежат на одной окружности. Сколько существует окружностей, каждая из которых проходит через три данные точки?
Сочетаний по три точки из одиннадцати будет 165. Три точки, не лежащие на одной прямой, составляют треугольник. Вокруг любого треугольника можно описать окружность только одну. Вокруг наших треугольников будет 165 окружностей.