Яхуб нарисовал множество из n точек на декартовой плоскости. Он назвал их «особыми точками». Четырехугольник — это многоугольник без самопересечений, имеющий четыре стороны (или ребра) и четыре вершины (или угла). Пожалуйста, обратите внимание, что четырехугольник может не быть выпуклым. Особый четырехугольник — это такой четырехугольник, в котором все четыре вершины принадлежат множеству особых точек. Вам дано множество особых точек. Пожалуйста, вычислите максимальную площадь особого четырехугольника.
В первой строке записано целое число n ( 4 ≤ n ≤ 300 ). В каждой из следующих n строк записано по два целых числа: x i, y i ( — 1000 ≤ x i, y i ≤ 1000) — декартовы координаты i -той особой точки. Гарантируется, что никакие три точки не лежат на одной прямой. Гарантируется, что никакие две точки не совпадают.
Выведите единственное вещественное число — максимальную площадь особого четырехугольника. Ответ будет считаться правильным, если его относительная или абсолютная погрешность не превышает 10 — 9 .
Видео:Геометрия 8. Урок 12 - Площадь четырехугольников. Формулы.Скачать

Максимальная площадь четырехугольника
Для четырех сторон четырехугольника a, b, c, d найдите максимально возможную площадь четырехугольника от заданных сторон.
Согласно формуле Бретшнейдера , площадь общего четырехугольника определяется как 
Здесь a, b, c, d — стороны четырехугольника, s — полупериметр четырехугольника, а углы — два противоположных угла.
Таким образом, эта формула максимизируется только тогда, когда противоположные углы суммируются с пи (180), тогда мы можем использовать упрощенную форму формулы Бретшнейдера, чтобы получить (максимальную) площадь K.
Эта формула называется формулой Брахмагупты .
Ниже приведена реализация данного подхода
// Программа CPP, чтобы найти максимум
// четырехугольник
#include
using namespace std;
double maxArea( double a, double b,
double c, double d)
double semiperimeter = (a + b + c + d) / 2;
// Применение формулы Брахмагупты к
// получаем максимальную площадь четырехугольника
return sqrt ((semiperimeter — a) *
double a = 1, b = 2, c= 1, d = 2;
printf ( «%.2fn» ,maxArea(a, b, c, d));
// Java-программа для поиска максимального значения
// четырехугольник
static double maxArea( double a, double b,
double c, double d)
double semiperimeter = (a + b + c + d) / 2 ;
// Применение формулы Брахмагупты к
// получаем максимальную площадь четырехугольника
return Math.sqrt((semiperimeter — a) *
public static void main (String[] args)
double a = 1 , b = 2 , c= 1 , d = 2 ;
System.out.println(maxArea(a, b, c, d));
// Этот код предоставлен sunnysingh
# Python3 программа для поиска максимума
# площадь четырехугольника
def maxArea (a , b , c , d ):
semiperimeter = (a + b + c + d) / 2
# Применение формулы Брахмагупты к
# получить максимальную площадь четырехугольника
return math.sqrt((semiperimeter — a) *
print ( «%.2f» % maxArea(a, b, c, d))
# Этот код предоставлен «Sharad_Bhardwaj».
// C # программа для поиска максимума
// четырехугольник
static double maxArea( double a, double b,
double c, double d)
double semiperimeter = (a + b + c + d) / 2;
// Применение формулы Брахмагупты к
// получаем максимальную площадь четырехугольника
return Math.Sqrt((semiperimeter — a) *
public static void Main ()
double a = 1, b = 2, c= 1, d = 2;
Console.WriteLine(maxArea(a, b, c, d));
// Этот код предоставлен vt_m.
// PHP-программа, чтобы найти максимум
// четырехугольник
function maxArea( $a , $b , $c , $d )
$semiperimeter = ( $a + $b + $c + $d ) / 2;
// Применение формулы Брахмагупты к
// получаем максимальную площадь четырехугольника
return sqrt(( $semiperimeter — $a ) *
$a = 1; $b = 2; $c = 1; $d = 2;
echo (maxArea( $a , $b , $c , $d ));
// Этот код предоставлен vt_m.
?>
Видео:ПЛОЩАДЬ ЧЕТЫРЕХУГОЛЬНИКА 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Формулы вычисления площади произвольного четырёхугольника
В школьных математических заданиях часто требуется определить площадь четырёхугольника. Все довольно просто, если задан частный случай фигуры — квадрат, ромб, прямоугольник, трапеция, параллелограмм, ромбоид. В случае же произвольного четырёхугольника все несколько сложнее, но также вполне доступно для среднего школьника. Ниже мы изучим различные методы расчётов площади произвольных четырёхугольников, запишем формулы и рассмотрим различные вспомогательные примеры.
Видео:Площадь четырехугольникаСкачать

Определения и соглашения
В приведённой ниже таблице будут указаны определения и договорённости, которые будут использоваться в дальнейшем во время наших рассуждений.
Четырёхугольник — это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
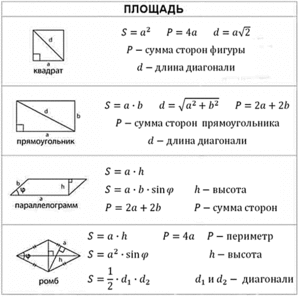
- Диагональ — отрезок, соединяющий вершины многоугольника не лежащие на одной стороне (её обозначение – латинская буква d).
- Площадь фигуры — это численное значение территории, заключённой внутри многоугольника (её обозначение – латинская буква S).
- Синус угла — это число равное отношению противоположного катета к гипотенузе в прямоугольном треугольнике. (её обозначение – запись sin).
- Косинус угла — это число равное отношению прилежащего катета к гипотенузе в прямоугольном треугольнике. В дальнейшем в статье для его обозначения будем использовать латинскую запись cos.
- Описанная окружность — это окружность, которой принадлежат все вершины многоугольника ( её радиуса обозается буквой R).
- Вписанная окружность — это окружность, которая касается всех сторон многоугольника. В дальнейшем в статье для обозначения её радиуса будем использовать латинскую букву r.
- Угол между сторонами a и b будем обозначать следующей записью (a,b).
Видео:Найдите площадь четырёхугольникаСкачать

Нахождение площади четырёхугольника различными способами и методами
Узнаем как найти площадь четырёхугольника когда даны его диагонали и образуемый при их пересечении острый угол. Тогда площадь четырёхугольника будет вычисляться по формуле: S = 1/2*d1*d2*sin(d1,d2).
Рассмотрим пример. Пусть d1 = 15 сантиметров, d2 = 12 сантиметров, и угол между ними 30 градусов. Определим S. S = 1/2*15*12*sin30 = 1/2*15*12*1/2 = 45 сантиметров квадратных.
Теперь пусть даны стороны и противолежащие углы четырёхугольника.
Пусть a, b, c, d известные стороны многоугольника; p — его полупериметр. Корень квадратный выражения условимся обозначать как rad (от латинского radical). Формула площади четырёхугольника будет находиться по формуле: S = rad(( p − a ) ( p − b ) ( p − c ) ( p − d ) − a b c d ⋅ c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d).
На первый взгляд, формула кажется очень сложной и вычурной. Однако ничего сложного здесь нет, что мы и докажем, рассмотрев пример. Пусть данные нашего условия следующие: a = 18 миллиметров, b = 23 миллиметра, c = 22 миллиметра, d = 17 миллиметров. Противолежащие углы будут равны (a,b) = 0,5 градуса и (c,d) = 1,5 градуса. Для начала находим полупериметр: p = 1/2*(18 + 23 + 22 + 17) = 1/2*80 = 40 миллиметров.
Теперь найдём квадрат косинуса полусуммы противолежащих углов: c o s^2( (a,b) + (c,d))/2) = c o s^2(0,5 + 1,5)/2 = c o s1*c o s1 = (1/2)*(1/2) = 0,9996.
Подставим полученные данные в нашу формулу, получим: S = rad((40 — 18)*(40 — 23)*(40 — 22)*(40 — 17) — 18*23*22*17*0,97) = rad(22*17*18*23 — 18*23*22*17*1/4) = rad((22*17*18*23*(1 — 0,9996)) = rad(154836*0,0004) = rad62 = 7,875 миллиметра квадратного.
Разберёмся как находить площадь с помощью вписанной и описанной окружностей. При решении задач данной темы имеет смысл сопровождать свои действия вспомогательным рисунком, хотя это требование и не является обязательным.
Если есть вписанная окружность и нужно найти площадь четырёхугольника формула имеет вид:
Снова возьмём на рассмотрение пример: a = 16 метров, b = 30 метров, c = 28 метров, d = 14 метров, r = 6 метров. Подставим аши значения в формулу, получим:
S = ((16 +30 + 28 + 14)/2)*6 = 44*6 = 264 метров квадратных.
Теперь займёмся вариантом когда окружность описана вокруг четырёхугольника. Здесь мы сможем воспользоваться следующей формулой:
S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине длины периметра. Пускай в нашем случае стороны имеют следующие значения a = 26 дециметров, b = 35 дециметров, c = 39 дециметров, d = 30 дециметров.
Первым делом определим полупериметр, p = (26 + 35 + 39 + 30)/2 = 65 дециметров. Подставим найденное значение в нашу формулу. Получим:
S = rad((65 — 26)*(65 — 35)*(65 — 39)*(65 — 30)) = rad(39*30*26*35) = 1032 (округлённо) дециметров квадратных.
Видео:КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

Заключение
Внимательно изучив все вышеизложенное, можно сделать вывод — определение площади произвольного четырёхугольника с разными сторонами сложнее, чем у них же специальных видов — квадрата, прямоугольника, ромба, трапеции, параллелограмма. Однако внимательно изучив все приведённые методы, можно с лёгкостью решать задачи необходимые для школьников. Сведём все наши формулы в одну таблицу:
- S = 1/2*d1*d2*sin(d1,d2);
- S = rad(( p − a )*( p − b )*( p − c )*( p − d ) − a*b*c*d*c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d);
- S = ((a + b+ c + d)/2)*r
S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине периметра.
Таким образом, реально сложной является только формула номер 2, но и она вполне доступна, при условии хорошего понимания данных в статье определений и соглашений.
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Видео
Разобраться в этой теме вам поможет видео.
🌟 Видео
Геометрия Как найти площадь четырехугольника, если нет формулыСкачать

Задача с канала PreMath — попробуй найти площадь четырехугольникаСкачать

Найти площадь четырехугольника!Скачать

Площадь одной клетки равна 1. Найдите площадь фигуры ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать
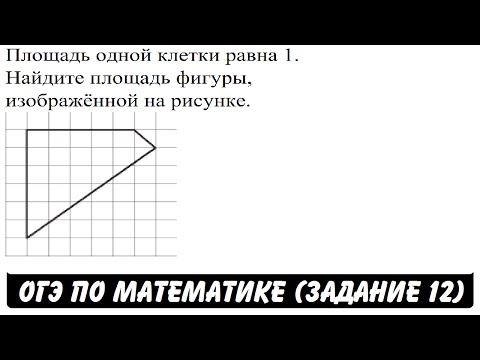
Площадь прямоугольника. Как найти площадь прямоугольника?Скачать

Площадь четырёхугольника через диагоналиСкачать

🤭3 ХИТРЫХ СПОСОБА ПОСТРОИТЬ СЕКРЕТНЫЙ ДОМ В МАЙНКРАФТ! ШЕДИ ЛЕСКА И НУБИК ТРОЛЛИНГ MINECRAFTСкачать

Вирусная задача. Найти площадь четырёхугольника.Скачать
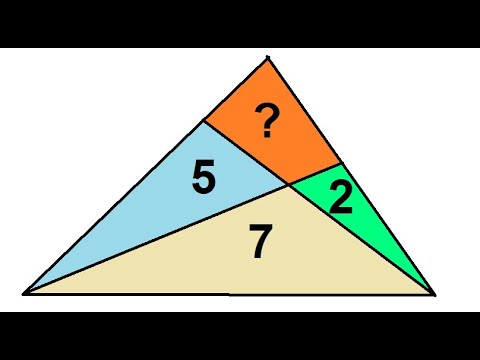
Геометрия 8. Урок 13 - Площадь четырехугольников. ЗадачиСкачать

Самый простой способ нахождения площадиСкачать

Площадь треугольника. Как найти площадь треугольника?Скачать

Геометрия: считаем ПЛОЩАДЬ ЧЕТЫРЕХУГОЛЬНИКА | Математика 8-11 классСкачать

Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Найдите площадь четырёхугольникаСкачать


 Четырёхугольник — это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
Четырёхугольник — это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.