Если Вы приняли решение заниматься рисованием профессионально, или академический рисунок необходим Вам для поступления в один из московских творческих вузов или на направление архитектура, то Вы не сможете обойтись без изучения рисунка врезок. Для того, чтобы говорить об особенностях рисунка, давайте рассмотрим само понятие и необходимость его изучения. Врезка — это композиция из простых геометрических фигур объединенных в единое тело.
Врезки изучаются на переходном этапе от гипсовых фигур к телам, которые относятся к живой природе или были созданы человеком. Мы знаем, что все сложные предметы состоят из простых фигур, поэтому понимание взаимодействия этих фигур между собой невероятно важно, для выполнения и построения качественной работы. Врезка как раз помогает усвоить то, как формы взаимодействуют друг с другом, как происходит процесс встраивания одной фигуры в другую. Результат освоения базового уровня академического рисунка — композиция из геометрических тел — врезка.
- Связка
- Какие навыки необходимы, чтобы приступить к изучению врезок?
- Рекомендации по созданию композиции из врезанных тел
- Как компоновать фигуры в листе
- Структура изобразительной плоскости
- Композиционное равновесие в рисовании
- Композиционный центр и второстепенные элементы
- Экзаменационные требования МАрхИ к композициям из врезанных тел
- Как научиться выполнять связки
- Сопряжения в инженерной графике на чертежах с примерами
- Сопряжение двух пересекающихся прямых линий
- Сопряжения прямой с окружностью
- Сопряжение двух окружностей
- Построение касательных
- Построение сопряжений
- Сопряжение (касание) прямой и окружности
- 🎦 Видео
Видео:ТЕМА 9. ОСНОВЫ КОМПОЗИЦИИ.Скачать

Связка
Кроме понятия врезки существует также понятие связки. Разберем, зачем необходимо изучение связок и врезок при обучении рисованию.
Связка — композиция,объемно-пространственная, которая состоит вписанных (или сочлененных) геометрических тел. Тела частично или полностью входят один в одно. Связка — это задание на развитие объемно-пространственного мышления, поэтому оно выполняется не с натуры, а по представлению. Это задание сложное и подразумевает, что у Вас есть необходимые базовые знание по академическому рисуyку. Приступать к нему можно после полного изучения простых фигур, а также отрисовке композиций их геометрических тел. Сложность задания состоит в том, что необходимо не только правильно построить предметы, но и сохранить все перспективные сокращения (в том числе при их сочленении), но и правильно передать все светотеневые отношения предметов. Для этого необходимо полностью и максимально четко представлять в воображении композицию тел, к работе следует приступать уже после того, как связка сформировалась у Вас в голове. В противном случае возможен ряд ошибок.
Каков полезный итог работы над врезками и связками? Вы сможете работать по воображению, формировать образ итогового предмета, работы без дополнительных подсказок. Понимать, как строятся конструкции сечений, как преломляются и видоизменяются грани в тех местах, где они преломляются. В процессе работы Вы будете использовать знания законов светотени, для того, чтобы правильно изобразить распределения света на предметах. Это способствуют закреплению знаний, которые были получены в процессе обучения академическому рисунку. Но самым главным позитивным результатом является развитое объемно-пространственное мышление столь необходимое для правильного изображения реальных предметов. Эти навыки Вы сможете применять уже в процессе рисунка композиции из бытовых предметов, а далее в изображении любых предметов. Зачастую требования к умению рисования врезок, связок и других композиций из геометрических тел выдвигают творческие и архитектурные вузы, но эти знания необходимы всем, кто работает в творческой сфере и занимается объемными телами.
Видео:Взаимное расположение окружности и прямой. 7 класс.Скачать

Какие навыки необходимы, чтобы приступить к изучению врезок?
Как мы уже обозначили ранее, к врезкам стоит переходить после того, как Вы усвоили базовый уровень академического рисунка, Вы должны четко понимать:
- как строятся основные геометрические тела, какие их свойства и особенности конструкции;
- как работает перспектива — воздушная и линейная, хорошо понимать перспективу и перспективные сокращения, а также знать законы светотени.
Вы должны иметь опыт рисунка не только с натуры, но и по воображению. Представлять, как взаимодействует предмет с пространством в разном положении.
Самое главное требование — уверенное владение простым карандашом. Без уверенного рисунка,умения проводить ровные, четкие линии, деления отрезков, Вы не сможете выполнить правильно врезку, так как при её рисунке запрещается использования любых вспомогательных инструментов, таких как циркуль, линейка.
Перед тем, как приступить к заданию, необходимо освоить работу над отдельными геометрическими телами и композициями из них. Также следует уверенно работать со светотенью и перспективными сокращениями. Если Вы освоили все эти базовые навыки, то можете смело приступать к рисунку связок.
Видео:1 2 4 сопряжение окружностейСкачать

Рекомендации по созданию композиции из врезанных тел
В качестве базового элемента следует выбирать кубы или четырехгранники, потому что в них проще врезать геометрические объекты большей сложности: цилиндры, шары и конусы. А чтобы не допустить ошибок при построении перспективы, используют специальную сетку, поскольку чем разнообразнее и многочисленнее геометрические тела, которые планируется включить в задуманную композицию, тем сложнее избежать недочетов, искажений и других ошибок, вне зависимости от качества основы. Однако построение сетки – весьма непростая задача, которая требует времени даже у продвинутого рисовальщика. Именно поэтому её построение следует изучать отдельно, но это того стоит – грамотное и верное построение сетки значительно уменьшит время в последующей работе над композицией.
Качество итогового изображения напрямую связано с точностью построений на этом этапе работы, ведь они – основа, и ошибаться здесь попросту нельзя. Поэтому, изучая врезанные тела, особенно важно обратить внимание на методы их сочленения. Эти связки (методы) классифицируются по уровням сложности, потому и знакомство с ними, конечно же, начинают с самых простых – с тел с плоскими гранями, а именно – кубами и четырёхгранными призмами.
Видимая часть врезанной геометрической фигуры служит для определения размеров, поэтому эти части должны занимать минимум половину от общего объёма. Например, при соединении с конусом, следует показать его основание, вершину и боковую поверхность.
Универсальный подход при выборе линии для врезки фигуры заключается в следующем: необходимо опираться на оси симметрии, высоты и другие линии и членения, предполагаемые в конструкции.
При этом границы врезания тел варьируются от одной трети до половины. Если они будут меньше или больше, тела получатся либо чересчур разреженными, будто практически не касаются друг друга, либо слишком плотными – настолько, что пропадёт понимание, из каких именно фигур они составлены. Оба случая не только провоцируют ощущение дисгармонии, но и являются ошибкой, нарушающей правила композиции.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Как компоновать фигуры в листе
Грамотная компоновка объектов в листе – важная составляющая успешной работы, поэтому если на первом этапе не уделить ей должного внимания или же допустить серьёзные ошибки, итоговое изображение получится как минимум неубедительным.
Даже опытным художникам допущенные ошибки не всегда заметны сразу – лишь к середине или ближе к завершению, когда исправить их не так просто. Для избежания этого нужно много практиковаться, быть особо аккуратными в создании сеток, уделять дополнительное внимание деталям, следовать логике на протяжении всей работы и регулярно проверять себя в процессе на наличие ошибок и недочётов, отдаляясь от изображения на некоторое расстояние. Иными словами, работа с врезанными объектами требует непрерывного анализа этих объектов, изучения их сечений, структуры и применения всех приобретённых знаний, позволяющих упростить работу с композицией.
То есть, выбор композиционного решения – достаточно сложный аналитический процесс по гармоничному размещению элементов в плоскости листа, включающий в себя и задачи художника, направленные на создание определённой эмоции в изображении.
Видео:7 класс, 21 урок, ОкружностьСкачать

Структура изобразительной плоскости
Оценка чистой плоскости даётся, исходя из особенностей восприятия человеком визуальной информации. Так, плоскость изначально подразумевает определённую структуру:
- горизонтальная ось;
- вертикальная ось;
- диагонали;
- центр.
От неё следует отталкиваться, представляя и продумывая ключевые элементы будущей композиции, поскольку в последующей работе над эскизами или составлением сетки именно эта структура ляжет в основу формирования реального изображения.
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Композиционное равновесие в рисовании
Гармония – одна из самых значимых композиционных задач, и достичь её можно различными способами. Уравновешенность изображения – один из основополагающих факторов её достижения. Это равновесие может быть динамичным или статичным – выбор обуславливается целями художника. Статичное равновесие опирается на вертикальные и горизонтальные оси, с использованием схожих по форме, массе или фактуре статичных объектов (кубов, призм). Динамичное же равновесие основывается на расположении основных элементов по диагональным осям и применении контрастов в фактуре, форме, и массе объектов, в их размерах, в тоновом и цветовом решениях всего изображения.
Если использованное равновесие – статичное, то внимание смотрящего рассредотачивается на всю плоскость изображения, если динамичное – зритель следует по условному маршруту, созданному художником, который начинается с ключевого объекта, и завершается попаданием в геометрический центр. А после зритель проходит этот путь ещё несколько раз.
Кроме того, чтобы достичь равновесия в композиции, следует помнить, что человек, в силу особенностей его анатомии и психологии, воспринимает объекты в пространстве с определёнными визуальными искажениями, что также необходимо учитывать в работе. Например, верхняя часть плоскости, условно разделённой посередине, кажется больше, нижняя – меньше, хотя по факту они одинаковы. Аналогично с этим, элемент, размещённый на пересечении диагональных осей (в самом центре), на итоговом изображении визуально будет смещаться вниз листа, и равновесие будет нарушено. Исходя из этого, композиционный центр следует располагать смещённым относительно геометрического. Но важно помнить, что направление этого смещения будет влиять непосредственно на характер работы и её эмоциональный посыл.
Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Композиционный центр и второстепенные элементы
Композиционный центр – доминанта работы. Ей служат все без исключения элементы изображения, они же её дополняют. Несмотря на различия второстепенных объектов, их значимости, каждый из них вносит одинаково незаменим в создании общей композиции. То есть, для гармоничного изображения все элементы равноценны, и каждый из них должен находиться на “своём” месте, решать конкретную задачу для создания общей целостности работы.
Композиционный центр, относительно других частей изображения, требует особо тщательной и кропотливой проработки. Самые популярные способы его создания: отличительный размер относительно других частей, форма, цвет, расположение и фактура.
Видео:Основы композиции. Урок 16. Составление формальной композиции из кругов. Статика и асимметрия.Скачать

Экзаменационные требования МАрхИ к композициям из врезанных тел
Ключевые критерии МАрхИ в оценке экзаменационных работ включают качество исполнения связок и всего изображения и выполнение определённых стандартов вуза:
- экзаменационный рисунок должен отвечать поставленной задаче;
- оценивается композиционная идея (её качество), гармоничность всей работы, её сложность;
- качество компоновки работы в листе;
- правильность построения и размещения отдельных тел с учётом перспективы, грамотность в работе с врезанными объектами;
- правильность выбора тонального решения;
- завершённость работы.
Понимание сути этих требований необходимо для успешной сдачи экзаменов, однако немаловажно и показать накопленные знания и умения, способность к аналитике, а ещё – способность к созданию небанальной работы в ограниченных условиях.
Видео:Сопряжение двух пересекающихся прямых. Урок 9. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Как научиться выполнять связки
Освоить создание композиций из врезанных геометрических объектов на уровне, позволяющем попасть в архитектурный вуз, практически невозможно самостоятельно и без большого объёма практики. Лишь поняв и отработав особенности базовых геометрических фигур и построения на их основе других тел, получится компоновать и реализовывать гармоничные, осознанные связки на высокого качества.
Видео:Приемы и правила композиции из кругов. Симметрия, асимметрия, статика и динамика. Основы дизайна.Скачать

Сопряжения в инженерной графике на чертежах с примерами
Содержание:
В очертаниях технических форм часто встречаются плавные переходы от од- ной линии к другой. Плавный переход одной линии в другую, выполненный при помощи промежуточной линии, называется сопряжением. Построение сопряжений основано на следующих положениях геометрии.
- Переход окружности в прямую будет плавным только тогда, когда заданная прямая является касательной к окружности (рис. 11а). Радиус окружности, проведенный в точку касания К, перпендикулярен к касательной прямой.
- Переход от одной окружности к другой в точке К только тогда будет плавным, когда окружности имеют в данной точке общую касательную (рис. 11б).
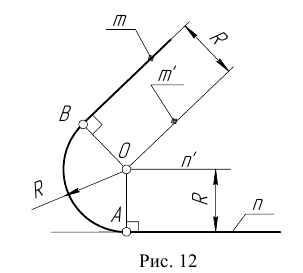
Точка касания К и центры окружностей
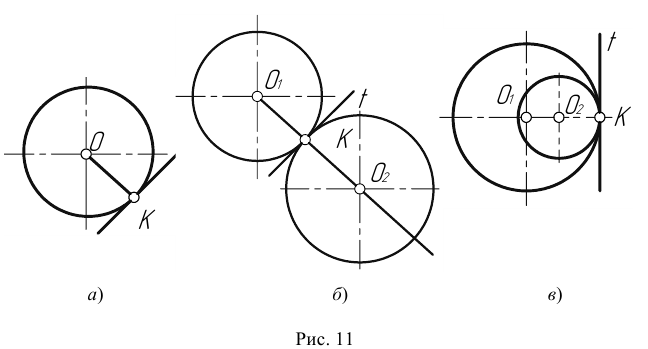
- Центром сопряжения О называется точка, равноудаленная от сопрягаемых линий (рис. 12).
- Точкой сопряжения А (В) называется точка касания двух сопрягаемых линий (рис. 12).
- Дуга сопряжения АВ – это дуга окружности, с помощью которой выполняется сопряжение (рис. 12).
- Радиус сопряжения R – это радиус дуги сопряжения (рис. 12).
Для выполнения сопряжений необходимо определить три элемента построения: 1) радиус сопряжения; 2) центр сопряжения; 3) точки сопряжения.
Видео:Окружность и круг, 6 классСкачать

Сопряжение двух пересекающихся прямых линий
Пусть даны две пересекающиеся прямые m, n и радиус сопряжения R (рис. 12). Необходимо построить сопряжение данных прямых дугой окружности радиусом R.
Выполним следующие построения:
- Построим множество точек центров сопряжения, удаленных от прямой n на расстояние радиуса R сопряжения. Таким множеством является прямая
параллельная данной прямой n и отстоящая от неё на расстояние R.
- Построим множество точек центров сопряжения, удаленных от прямой m на расстояние радиуса сопряжения. Таким множеством является прямая
параллельная m и отстоящая от последней на расстояние R.
- В пересечении построенных прямых
найдем центр сопряжения О.
- Определим точку А сопряжения на прямой n. Для этого опустим из центра О перпендикуляр на прямую n . Для определения точки сопряжения В на прямой m необходимо опустить соответственно перпендикуляр из центра О на прямую m.
Проведем дугу сопряжения AB. Теперь будут определены все элементы сопряжения: радиус, центр и точки сопряжения.
Видео:Касательные к окружностиСкачать

Сопряжения прямой с окружностью
Сопряжение прямой с окружностью может быть внешним или внутренним. Рассмотрим построение внешнего сопряжения прямой с окружностью.
Пример 1. Пусть задана окружность радиусом R с центром в точке 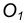
Для решения задачи выполним следующие построения:
- Построим множество точек центров сопряжения, удаленных от сопрягаемой прямой на расстояние R. Это множество задает прямая
параллельная m и отстоящая от неё на расстояние R.
- Множество точек центров сопряжения, удаленных от окружности n на рас- стояние R, есть окружность
проведенная радиусом
- Центр сопряжения О находим как точку пересечения линий
- Точку сопряжения А находим как основание перпендикуляра, проведенного из точки О на прямую m. Чтобы построить точку сопряжения В, необходимо про- вести линию центров
т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.
- Проведем дугу сопряжения АВ.
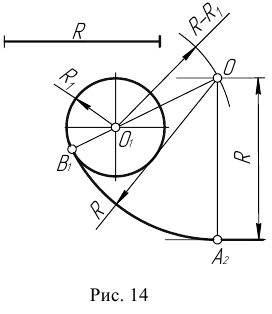
Пример 2. При построении внутреннего сопряжения (рис. 14) последовательность построений остается та же, что и в примере 1. Однако центр сопряжения определяется с помощью вспомогательной дуги окружности, проведенной из центра 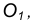
Видео:Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

Сопряжение двух окружностей
Сопряжение двух окружностей может быть внешним, внутренним и смешанным. Пусть задан радиус сопряжения R, а центры сопряжения и точки сопряжения следует найти.
Пример 1. Построим сопряжение с внешним касанием двух данных окружностей m и n с радиусами 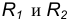
- Для нахождения центра сопряжения О проведем окружность
удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности
равен
- Радиусом
проведем окружность
, удаленную от данной окружности n на расстояние R.
- Найдем центр сопряжения О как точку пересечения окружностей
.
- Найдем точку сопряжения А как пересечение линии центров
с дугой m.
- Аналогично найдем точку В как пересечение линии центров
с дугой n .
- Проведем дугу сопряжения АВ.
Пример 2. Построим сопряжение с внутренним касанием двух данных окружностей m и n с радиусами 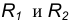
- Для нахождения центра сопряжения О проведем окружность
на расстоянии
от данной окружности m.
- Проведем окружность
на расстоянии
от данной окружности n.
- Центр сопряжения О найдем как точку пересечения окружностей
- Точку сопряжения А найдем как точку пересечения линии центров
с заданной окружностью m.
- Точку сопряжения В найдем как точку пересечения линии центров
c заданной окружностью n.
- Проведем дугу сопряжения AВ с центром в точке O.
Пример 3. На рис. 16 приведен пример построения сопряжения с внешне- внутренним касанием.
Видео:Расстояние между центрами вписанной и описанной окружностей треугольника и их радиусами #ShortsСкачать

Построение касательных
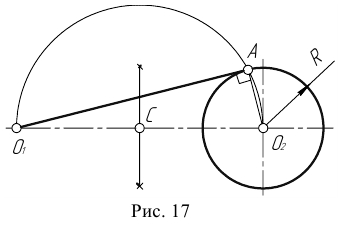
Пример 1. Дана окружность с центром в точке 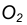
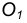
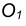
Для решения задачи выполним следующие построения.
- Соединим точку
с центром окружности
- Находим середину С отрезка
- Из точки С, как из центра, проведем вспомогательную окружность радиусом
- В точке пересечения вспомогательной окружности с заданной получим точку касания А. Соединим точку
с точкой А.
Пример 2. Построим общую касательную АВ к двум заданным окружностям радиусов 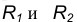
- Находим середину С отрезка
- Из точки С, как из центра, радиусом
проведем вспомогательную окружность.
- Из центра большей окружности
проведем вторую вспомогательную окружность радиусом
- Пересечение двух вспомогательных окружностей определяет точку К, через которую проходит радиус
идущий в точку касания В. 5. Для построения второй точки касания А проведем
- Соединим точки А и В отрезком прямой линии.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Нанесение размеров на чертежах
- Резьба на чертеже
- Соединения разъемные и неразъемные в инженерной графике
- Виды конструкторских документов
- Виды в инженерной графике
- Разрезы в инженерной графике
- Сечения в инженерной графике
- Выносные элементы в инженерной графике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Деление окружности на 3, 4, 5, 6 и 7 равных частейСкачать

Построение сопряжений
Часто при изображении на чертеже контура детали приходится выполнять плавный переход одной линии в другую (плавный переход между прямыми линиями или окружностями) для выполнения конструктивных и технологических требований. Плавный переход одной линии в другую называют сопряжением.
Для построения сопряжений необходимо определить:
- • центры сопряжений (центры, из которых проводят дуги);
- • точки касания/точки сопряжения (точки, в которых одна линия переходит в другую);
- • радиус сопряжения (если он нс задан).
Рассмотрим основные типы сопряжений.
Видео:Взаимное расположение окружностей. 7 класс.Скачать

Сопряжение (касание) прямой и окружности
Построение прямой, касательной к окружности. При построении сопряжения прямой и окружности используется известный признак касания этих линий: прямая, касательная к окружности, составляет прямой угол с радиусом, проведенным в точку касания (рис. 1.12).
Рис. 1.12. Касание прямой и окружности:
К — точка касания
Для проведения касательной к окружности через точку Л, лежащую вне окружности, необходимо:
- 1) соединить заданную точку А (рис. 1.13) с центром окружности О;
- 2) отрезок ОА разделить пополам (ОС = СА, см. рис. 1.7) и провести вспомогательную окружность радиусом СО (или СА);
Рис. 1.13. Построение касательной прямой к окружности
3) точку /С, (или К.» поскольку задача имеет два решения) соединить с точкой А.
Линия АК^ (или АК.,) является касательной к заданной окружности. Точки Ki и К2— точки касания.
Следует отметить, что рис. 1.13 иллюстрирует также один из способов точного графического построения двух перпендикулярных прямых (касательной и радиуса).
Построение прямой, касательной к двум окружностям. Обращаем внимание читателя на то, что задачу построения прямой, касательной к двум окружностям, можно рассматривать как обобщенный случай предыдущей задачи (построение касательной из точки к окружности). Сходство этих задач прослеживается из рис. 1.13 и 1.14.
Внешнее касание двух окружностей. При внешнем касании (см. рис. 1.14) обе окружности лежат но одну сторону от прямой.
На рис. 1.14 изображены малая окружность радиусом R с центром в точке А и большая окружность радиусом R< с центром в точ-
Рис. 1.14. Построение внешней касательной к двум окружностям ке О. Чтобы построить внешнюю касательную к этим окружностям, необходимо выполнить следующие действия:
- 1) через центр О большей окружности провести вспомогательную окружность радиусом (/?, — R);
- 2) построить касательные к вспомогательной окружности из точки А (центр малой окружности). Точки К< и К., — точки касания прямых и окружности (заметим, что задача имеет два решения);
- 3) точки К< и К2 соединить с центром О и продолжить эти линии до пересечения с окружностью радиусом Rv Точки пересечения Кли /С, являются точками касания (сопряжения);
- 4) через точку А провести радиусы, параллельные линиям ()КЛи ОКг Точки пересечения этих радиусов с малой окружностью — точки К-и Кл являются точками касания (сопряжения);
- 5) соединив точки Кл и /С(;, а также Кл и К5, получить искомые касательные.
Внутреннее касание двух окружностей (окружности лежат по разные стороны от прямой, рис. 1.15) выполняется по аналогии с внешнем касанием, с той лишь разницей, что через центр О большей окружности проводится вспомогательная окружность радиусом /?, + R. Па рис. 1.15 изображено два возможных решения задачи.
Рис. 1.1 5. Построение внутренней касательной к двум окружностям
Сопряжение пересекающихся прямых дугой окружности заданным радиусом. Построение (рис. 1.16) сводится к построению окружности радиусом R, касающейся одновременно обеих заданных линий.
Для нахождения центра этой окружности проводим две вспомогательные прямые, параллельные заданным, на расстоянии R от каждой из них. Точка пересечения этих прямых является центром О дуги сопряжения. Перпендикуляры, опущенные из центра О на заданные прямые, определяют точки сопряжения (касания) /С, и К2.
Рис. 1.16. Сопряжение пересекающихся прямых дугой окружности
Рис. 1.17. Построение сопряжения окружности и прямой дугой заданным радиусом R:
а — внутреннее касание; б — внешнее касание
Сопряжение окружности и прямой дугой заданным радиусом.
Примеры построения сопряжений окружности и прямой дугой заданным радиусом R приведены на рис. 1.17.
🎦 Видео
Построение касательной к окружностиСкачать

СОПРЯЖЕНИЕ ОКРУЖНОСТИ С ЛИНИЕЙ [pairing the circle with the line]Скачать
![СОПРЯЖЕНИЕ ОКРУЖНОСТИ С ЛИНИЕЙ [pairing the circle with the line]](https://i.ytimg.com/vi/oKj3m1n67wI/0.jpg)
Параллельные прямые | Математика | TutorOnlineСкачать

8 класс, 31 урок, Взаимное расположение прямой и окружностиСкачать










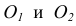
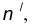 параллельная данной прямой n и отстоящая от неё на расстояние R.
параллельная данной прямой n и отстоящая от неё на расстояние R.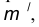 параллельная m и отстоящая от последней на расстояние R.
параллельная m и отстоящая от последней на расстояние R.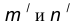 найдем центр сопряжения О.
найдем центр сопряжения О.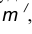 параллельная m и отстоящая от неё на расстояние R.
параллельная m и отстоящая от неё на расстояние R.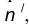 проведенная радиусом
проведенная радиусом 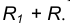
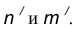
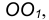 т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.
т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.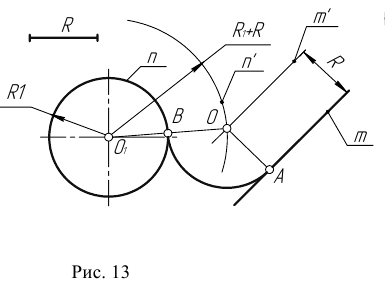
 удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности
удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности 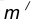 равен
равен 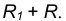
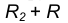 проведем окружность
проведем окружность 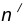 , удаленную от данной окружности n на расстояние R.
, удаленную от данной окружности n на расстояние R.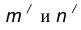 .
.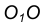 с дугой m.
с дугой m.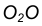 с дугой n .
с дугой n .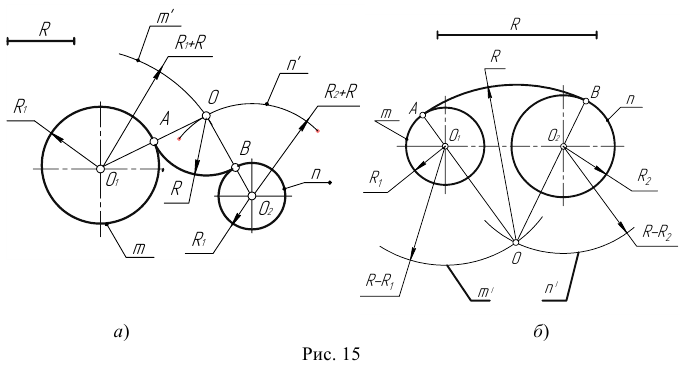
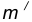 на расстоянии
на расстоянии 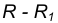 от данной окружности m.
от данной окружности m.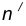 на расстоянии
на расстоянии 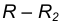 от данной окружности n.
от данной окружности n.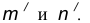
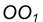 с заданной окружностью m.
с заданной окружностью m.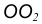 c заданной окружностью n.
c заданной окружностью n.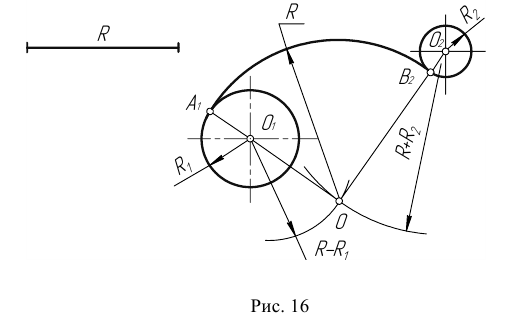
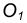 с центром окружности
с центром окружности 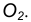
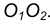
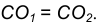
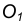 с точкой А.
с точкой А.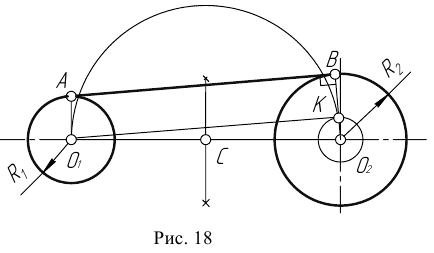
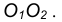
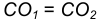 проведем вспомогательную окружность.
проведем вспомогательную окружность.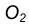 проведем вторую вспомогательную окружность радиусом
проведем вторую вспомогательную окружность радиусом 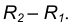
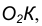 идущий в точку касания В. 5. Для построения второй точки касания А проведем
идущий в точку касания В. 5. Для построения второй точки касания А проведем