Знание — сила. Познавательная информация
- Касательная параллельна прямой
- Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной
- Определения и понятия
- Геометрический смысл производной функции в точке
- Уравнение касательной прямой
- Касательная к окружности, эллипсу, гиперболе, параболе
- Касательная к окружности
- Касательная к эллипсу
- Касательная к гиперболе
- Касательная к параболе
- Решение задач на геометрический смысл производной — справочник студента
- Обучающие карточки «Геометрический смысл производной»
- Геометрический смысл производной
- Геометрический смысл производной
- Как подготовиться к экзамену?
- Самая удобная и увлекательная подготовка к ЕГЭ
- Основные правила дифференцирования
- Физический смысл производной
- Геометрический смысл производной
- Геометрический смысл производной в заданиях КИМ ЕГЭ. — презентация
- 📸 Видео
Видео:№ 40130 РешуЕгэ найти абсциссу точки, в которой касательная к графику функции параллельна прямойСкачать

Касательная параллельна прямой
Задания из №7 ЕГЭ, в которых известно, что касательная к графику функции параллельна данной прямой, могут быть связаны как с графиком функции, так и с графиком производной. Поэтому очень важно внимательно читать условие.
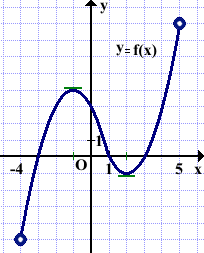
1) На рисунке изображен график функции y=f(x), определённой на интервале(-4;8). Найти количество точек, в которых касательная к графику функции параллельна прямой y=12 или совпадает с ней.
Касательная к графику функции параллельна оси абсцисс, а значит, и любой прямой вида y=b, где b — число, в точках экстремума, в которых производная существует, и в точках перегиба. То есть это задание аналогично заданию на определение точек графика функции, в которых производная равна нулю.
На графике данной функции y=f(x) таких точке две (с абсциссами x=-1 и x=2). Значит, касательная к графику функции параллельна прямой y=12 в двух точках.
Теперь рассмотрим аналогичное задание, в котором дан график производной функции.
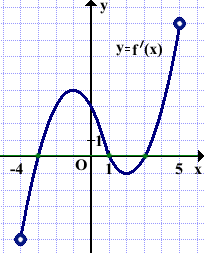
Угловой коэффициент касательной равен значению производной в точке касания: k2=f'(xo).
Значит, ищем точки, в которых значение производной равно нулю.
Таких точек три (с абсциссами x=-3, x=1 и x=3).
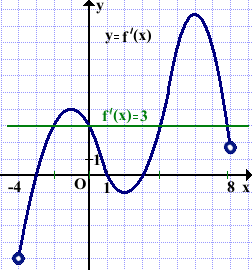
Поэтому ищем точки, в которых значение производной равно 3.
Таких точек в данном примере четыре.
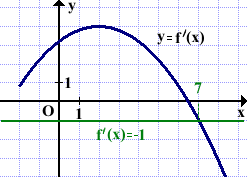
Ищем точку, в которой значение производной равно -1. Абсцисса этой точки xo=7.
Видео:Задание 7 ЕГЭ по математикеСкачать

Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной
Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.
Видео:Задача 7 ЕГЭ по математике #5Скачать

Определения и понятия
Угол наклона прямой y = k x + b называется угол α , который отсчитывается от положительного направления оси о х к прямой y = k x + b в положительном направлении.
На рисунке направление о х обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.
Угловой коэффициент прямой y = k x + b называют числовым коэффициентом k .
Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k = t g α .
- Угол наклона прямой равняется 0 только при параллельности о х и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0 . Значит, вид уравнения будет y = b .
- Если угол наклона прямой y = k x + b острый, тогда выполняются условия 0 α π 2 или 0 ° α 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α > 0 , причем имеется возрастание графика.
- Если α = π 2 , тогда расположение прямой перпендикулярно о х . Равенство задается при помощи равенства x = c со значением с , являющимся действительным числом.
- Если угол наклона прямой y = k x + b тупой, то соответствует условиям π 2 α π или 90 ° α 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.
Определение 3
Секущей называют прямую, которая проходит через 2 точки функции f ( x ) . Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.
По рисунку видно, что А В является секущей, а f ( x ) – черная кривая, α — красная дуга, означающая угол наклона секущей.
Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника А В С можно найти по отношению противолежащего катета к прилежащему.
Получаем формулу для нахождения секущей вида:
k = t g α = B C A C = f ( x B ) — f x A x B — x A , где абсциссами точек А и В являются значения x A , x B , а f ( x A ) , f ( x B ) — это значения функции в этих точках.
Очевидно, что угловой коэффициент секущей определен при помощи равенства k = f ( x B ) — f ( x A ) x B — x A или k = f ( x A ) — f ( x B ) x A — x B , причем уравнение необходимо записать как y = f ( x B ) — f ( x A ) x B — x A · x — x A + f ( x A ) или
y = f ( x A ) — f ( x B ) x A — x B · x — x B + f ( x B ) .
Секущая делит график визуально на 3 части: слева от точки А , от А до В , справа от В . На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.
По определению видно, что прямая и ее секущая в данном случае совпадают.
Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у = 0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.
Касательная к графику функции f ( x ) в точке x 0 ; f ( x 0 ) называется прямая, проходящая через заданную точку x 0 ; f ( x 0 ) , с наличием отрезка, который имеет множество значений х , близких к x 0 .
Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y = x + 1 , считается касательной к y = 2 x в точке с координатами ( 1 ; 2 ) . Для наглядности, необходимо рассмотреть графики с приближенными к ( 1 ; 2 ) значениями. Функция y = 2 x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.
Очевидно, что y = 2 x сливается с прямой у = х + 1 .
Для определения касательной следует рассмотреть поведение касательной А В при бесконечном приближении точки В к точке А . Для наглядности приведем рисунок.
Секущая А В , обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной α x .
Касательной к графику функции y = f ( x ) в точке А считается предельное положение секущей А В при В стремящейся к А , то есть B → A .
Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.
Видео:ЕГЭ 2017 Профильный №7 касательная к графику параллельна прямой #7Скачать

Геометрический смысл производной функции в точке
Перейдем к рассмотрению секущей А В для функции f ( x ) , где А и В с координатами x 0 , f ( x 0 ) и x 0 + ∆ x , f ( x 0 + ∆ x ) , а ∆ x обозначаем как приращение аргумента. Теперь функция примет вид ∆ y = ∆ f ( x ) = f ( x 0 + ∆ x ) — f ( ∆ x ) . Для наглядности приведем в пример рисунок.
Рассмотрим полученный прямоугольный треугольник А В С . Используем определение тангенса для решения, то есть получим отношение ∆ y ∆ x = t g α . Из определения касательной следует, что lim ∆ x → 0 ∆ y ∆ x = t g α x . По правилу производной в точке имеем, что производную f ( x ) в точке x 0 называют пределом отношений приращения функции к приращению аргумента, где ∆ x → 0 , тогда обозначим как f ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x .
Отсюда следует, что f ‘ ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x , где k x обозначают в качестве углового коэффициента касательной.
То есть получаем, что f ’ ( x ) может существовать в точке x 0 причем как и касательная к заданному графику функции в точке касания равной x 0 , f 0 ( x 0 ) , где значение углового коэффициента касательной в точке равняется производной в точке x 0 . Тогда получаем, что k x = f ‘ ( x 0 ) .
Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.
Видео:Задача 7 ЕГЭ по математикеСкачать

Уравнение касательной прямой
Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x 0 при пересечении.
Уравнение касательной к графику функции y = f ( x ) в точке x 0 , f 0 ( x 0 ) принимает вид y = f ‘ ( x 0 ) · x — x 0 + f ( x 0 ) .
Имеется в виду, что конечным значением производной f ‘ ( x 0 ) можно определить положение касательной, то есть вертикально при условии lim x → x 0 + 0 f ‘ ( x ) = ∞ и lim x → x 0 — 0 f ‘ ( x ) = ∞ или отсутствие вовсе при условии lim x → x 0 + 0 f ‘ ( x ) ≠ lim x → x 0 — 0 f ‘ ( x ) .
Расположение касательной зависит от значения ее углового коэффициента k x = f ‘ ( x 0 ) . При параллельности к оси о х получаем, что k k = 0 , при параллельности к о у — k x = ∞ , причем вид уравнения касательной x = x 0 возрастает при k x > 0 , убывает при k x 0 .
Произвести составление уравнения касательной к графику функции y = e x + 1 + x 3 3 — 6 — 3 3 x — 17 — 3 3 в точке с координатами ( 1 ; 3 ) с определением угла наклона.
Решение
По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, ( 1 ; 3 ) является точкой касания, тогда x 0 = — 1 , f ( x 0 ) = — 3 .
Необходимо найти производную в точке со значением — 1 . Получаем, что
y ‘ = e x + 1 + x 3 3 — 6 — 3 3 x — 17 — 3 3 ‘ = = e x + 1 ‘ + x 3 3 ‘ — 6 — 3 3 x ‘ — 17 — 3 3 ‘ = e x + 1 + x 2 — 6 — 3 3 y ‘ ( x 0 ) = y ‘ ( — 1 ) = e — 1 + 1 + — 1 2 — 6 — 3 3 = 3 3
Значение f ’ ( x ) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.
Тогда k x = t g α x = y ‘ ( x 0 ) = 3 3
Отсюда следует, что α x = a r c t g 3 3 = π 6
Ответ: уравнение касательной приобретает вид
y = f ‘ ( x 0 ) · x — x 0 + f ( x 0 ) y = 3 3 ( x + 1 ) — 3 y = 3 3 x — 9 — 3 3
Для наглядности приведем пример в графической иллюстрации.
Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.
Выяснить наличие существования касательной к графику заданной функции
y = 3 · x — 1 5 + 1 в точке с координатами ( 1 ; 1 ) . Составить уравнение и определить угол наклона.
Решение
По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.
Перейдем к нахождению производной
y ‘ = 3 · x — 1 5 + 1 ‘ = 3 · 1 5 · ( x — 1 ) 1 5 — 1 = 3 5 · 1 ( x — 1 ) 4 5
Если x 0 = 1 , тогда f ’ ( x ) не определена, но пределы записываются как lim x → 1 + 0 3 5 · 1 ( x — 1 ) 4 5 = 3 5 · 1 ( + 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ и lim x → 1 — 0 3 5 · 1 ( x — 1 ) 4 5 = 3 5 · 1 ( — 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ , что означает существование вертикальной касательной в точке ( 1 ; 1 ) .
Ответ: уравнение примет вид х = 1 , где угол наклона будет равен π 2 .
Для наглядности изобразим графически.
Найти точки графика функции y = 1 15 x + 2 3 — 4 5 x 2 — 16 5 x — 26 5 + 3 x + 2 , где
- Касательная не существует;
- Касательная располагается параллельно о х ;
- Касательная параллельна прямой y = 8 5 x + 4 .
Решение
Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x ∈ — ∞ ; 2 и [ — 2 ; + ∞ ) . Получаем, что
y = — 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ — ∞ ; — 2 1 15 x 3 — 6 x 2 + 9 x + 12 , x ∈ [ — 2 ; + ∞ )
Необходимо продифференцировать функцию. Имеем, что
y ‘ = — 1 15 x 3 + 18 x 2 + 105 x + 176 ‘ , x ∈ — ∞ ; — 2 1 15 x 3 — 6 x 2 + 9 x + 12 ‘ , x ∈ [ — 2 ; + ∞ ) ⇔ y ‘ = — 1 5 ( x 2 + 12 x + 35 ) , x ∈ — ∞ ; — 2 1 5 x 2 — 4 x + 3 , x ∈ [ — 2 ; + ∞ )
Когда х = — 2 , тогда производная не существует, потому что односторонние пределы не равны в этой точке:
lim x → — 2 — 0 y ‘ ( x ) = lim x → — 2 — 0 — 1 5 ( x 2 + 12 x + 35 = — 1 5 ( — 2 ) 2 + 12 ( — 2 ) + 35 = — 3 lim x → — 2 + 0 y ‘ ( x ) = lim x → — 2 + 0 1 5 ( x 2 — 4 x + 3 ) = 1 5 — 2 2 — 4 — 2 + 3 = 3
Вычисляем значение функции в точке х = — 2 , где получаем, что
- y ( — 2 ) = 1 15 — 2 + 2 3 — 4 5 ( — 2 ) 2 — 16 5 ( — 2 ) — 26 5 + 3 — 2 + 2 = — 2 , то есть касательная в точке ( — 2 ; — 2 ) не будет существовать.
- Касательная параллельна о х , когда угловой коэффициент равняется нулю. Тогда k x = t g α x = f ‘ ( x 0 ) . То есть необходимо найти значения таких х , когда производная функции обращает ее в ноль. То есть значения f ’ ( x ) и будут являться точками касания, где касательная является параллельной о х .
Когда x ∈ — ∞ ; — 2 , тогда — 1 5 ( x 2 + 12 x + 35 ) = 0 , а при x ∈ ( — 2 ; + ∞ ) получаем 1 5 ( x 2 — 4 x + 3 ) = 0 .
— 1 5 ( x 2 + 12 x + 35 ) = 0 D = 12 2 — 4 · 35 = 144 — 140 = 4 x 1 = — 12 + 4 2 = — 5 ∈ — ∞ ; — 2 x 2 = — 12 — 4 2 = — 7 ∈ — ∞ ; — 2 1 5 ( x 2 — 4 x + 3 ) = 0 D = 4 2 — 4 · 3 = 4 x 3 = 4 — 4 2 = 1 ∈ — 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ — 2 ; + ∞
Вычисляем соответствующие значения функции
y 1 = y — 5 = 1 15 — 5 + 2 3 — 4 5 — 5 2 — 16 5 — 5 — 26 5 + 3 — 5 + 2 = 8 5 y 2 = y ( — 7 ) = 1 15 — 7 + 2 3 — 4 5 ( — 7 ) 2 — 16 5 — 7 — 26 5 + 3 — 7 + 2 = 4 3 y 3 = y ( 1 ) = 1 15 1 + 2 3 — 4 5 · 1 2 — 16 5 · 1 — 26 5 + 3 1 + 2 = 8 5 y 4 = y ( 3 ) = 1 15 3 + 2 3 — 4 5 · 3 2 — 16 5 · 3 — 26 5 + 3 3 + 2 = 4 3
Отсюда — 5 ; 8 5 , — 4 ; 4 3 , 1 ; 8 5 , 3 ; 4 3 считаются искомыми точками графика функции.
Рассмотрим графическое изображение решения.
Черная линия – график функции, красные точки – точки касания.
- Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 8 5 . Для этого нужно решить уравнение вида y ‘ ( x ) = 8 5 . Тогда, если x ∈ — ∞ ; — 2 , получаем, что — 1 5 ( x 2 + 12 x + 35 ) = 8 5 , а если x ∈ ( — 2 ; + ∞ ) , тогда 1 5 ( x 2 — 4 x + 3 ) = 8 5 .
Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что
— 1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 — 4 · 43 = — 28 0
Другое уравнение имеет два действительных корня, тогда
1 5 ( x 2 — 4 x + 3 ) = 8 5 x 2 — 4 x — 5 = 0 D = 4 2 — 4 · ( — 5 ) = 36 x 1 = 4 — 36 2 = — 1 ∈ — 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ — 2 ; + ∞
Перейдем к нахождению значений функции. Получаем, что
y 1 = y ( — 1 ) = 1 15 — 1 + 2 3 — 4 5 ( — 1 ) 2 — 16 5 ( — 1 ) — 26 5 + 3 — 1 + 2 = 4 15 y 2 = y ( 5 ) = 1 15 5 + 2 3 — 4 5 · 5 2 — 16 5 · 5 — 26 5 + 3 5 + 2 = 8 3
Точки со значениями — 1 ; 4 15 , 5 ; 8 3 являются точками, в которых касательные параллельны прямой y = 8 5 x + 4 .
Ответ: черная линия – график функции, красная линия – график y = 8 5 x + 4 , синяя линия – касательные в точках — 1 ; 4 15 , 5 ; 8 3 .
Возможно существование бесконечного количества касательных для заданных функций.
Написать уравнения всех имеющихся касательных функции y = 3 cos 3 2 x — π 4 — 1 3 , которые располагаются перпендикулярно прямой y = — 2 x + 1 2 .
Решение
Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется — 1 , то есть записывается как k x · k ⊥ = — 1 . Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k ⊥ = — 2 , тогда k x = — 1 k ⊥ = — 1 — 2 = 1 2 .
Теперь необходимо найти координаты точек касания. Нужно найти х , после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x 0 получаем, что k x = y ‘ ( x 0 ) . Из данного равенства найдем значения х для точек касания.
y ‘ ( x 0 ) = 3 cos 3 2 x 0 — π 4 — 1 3 ‘ = 3 · — sin 3 2 x 0 — π 4 · 3 2 x 0 — π 4 ‘ = = — 3 · sin 3 2 x 0 — π 4 · 3 2 = — 9 2 · sin 3 2 x 0 — π 4 ⇒ k x = y ‘ ( x 0 ) ⇔ — 9 2 · sin 3 2 x 0 — π 4 = 1 2 ⇒ sin 3 2 x 0 — π 4 = — 1 9
Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.
3 2 x 0 — π 4 = a r c sin — 1 9 + 2 πk или 3 2 x 0 — π 4 = π — a r c sin — 1 9 + 2 πk
3 2 x 0 — π 4 = — a r c sin 1 9 + 2 πk или 3 2 x 0 — π 4 = π + a r c sin 1 9 + 2 πk
x 0 = 2 3 π 4 — a r c sin 1 9 + 2 πk или x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z
Z — множество целых чисел.
Найдены х точек касания. Теперь необходимо перейти к поиску значений у :
y 0 = 3 cos 3 2 x 0 — π 4 — 1 3
y 0 = 3 · 1 — sin 2 3 2 x 0 — π 4 — 1 3 или y 0 = 3 · — 1 — sin 2 3 2 x 0 — π 4 — 1 3
y 0 = 3 · 1 — — 1 9 2 — 1 3 или y 0 = 3 · — 1 — — 1 9 2 — 1 3
y 0 = 4 5 — 1 3 или y 0 = — 4 5 + 1 3
Отсюда получаем, что 2 3 π 4 — a r c sin 1 9 + 2 πk ; 4 5 — 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; — 4 5 + 1 3 являются точками касания.
Ответ: необходимы уравнения запишутся как
y = 1 2 x — 2 3 π 4 — a r c sin 1 9 + 2 πk + 4 5 — 1 3 , y = 1 2 x — 2 3 5 π 4 + a r c sin 1 9 + 2 πk — 4 5 + 1 3 , k ∈ Z
Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.
Рисунок показывает, что расположение функции идет на промежутке [ — 10 ; 10 ] , где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y = — 2 x + 1 2 . Красные точки – это точки касания.
Видео:Касательная параллельна прямой 7 задание проф. ЕГЭ по математикеСкачать

Касательная к окружности, эллипсу, гиперболе, параболе
Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.
Касательная к окружности
Для задания окружности с центром в точке x c e n t e r ; y c e n t e r и радиусом R применяется формула x — x c e n t e r 2 + y — y c e n t e r 2 = R 2 .
Данное равенство может быть записано как объединение двух функций:
y = R 2 — x — x c e n t e r 2 + y c e n t e r y = — R 2 — x — x c e n t e r 2 + y c e n t e r
Первая функция располагается вверху, а вторая внизу, как показано на рисунке.
Для составления уравнения окружности в точке x 0 ; y 0 , которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y = R 2 — x — x c e n t e r 2 + y c e n t e r или y = — R 2 — x — x c e n t e r 2 + y c e n t e r в указанной точке.
Когда в точках x c e n t e r ; y c e n t e r + R и x c e n t e r ; y c e n t e r — R касательные могут быть заданы уравнениями y = y c e n t e r + R и y = y c e n t e r — R , а в точках x c e n t e r + R ; y c e n t e r и
x c e n t e r — R ; y c e n t e r будут являться параллельными о у , тогда получим уравнения вида x = x c e n t e r + R и x = x c e n t e r — R .
Касательная к эллипсу
Когда эллипс имеет центр в точке x c e n t e r ; y c e n t e r с полуосями a и b , тогда он может быть задан при помощи уравнения x — x c e n t e r 2 a 2 + y — y c e n t e r 2 b 2 = 1 .
Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что
y = b a · a 2 — ( x — x c e n t e r ) 2 + y c e n t e r y = — b a · a 2 — ( x — x c e n t e r ) 2 + y c e n t e r
Если касательные располагаются на вершинах эллипса, тогда они параллельны о х или о у . Ниже для наглядности рассмотрим рисунок.
Написать уравнение касательной к эллипсу x — 3 2 4 + y — 5 2 25 = 1 в точках со значениями x равного х = 2 .
Решение
Необходимо найти точки касания, которые соответствуют значению х = 2 . Производим подстановку в имеющееся уравнение эллипса и получаем, что
x — 3 2 4 x = 2 + y — 5 2 25 = 1 1 4 + y — 5 2 25 = 1 ⇒ y — 5 2 = 3 4 · 25 ⇒ y = ± 5 3 2 + 5
Тогда 2 ; 5 3 2 + 5 и 2 ; — 5 3 2 + 5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.
Перейдем к нахождению и разрешению уравнения эллипса относительно y . Получим, что
x — 3 2 4 + y — 5 2 25 = 1 y — 5 2 25 = 1 — x — 3 2 4 ( y — 5 ) 2 = 25 · 1 — x — 3 2 4 y — 5 = ± 5 · 1 — x — 3 2 4 y = 5 ± 5 2 4 — x — 3 2
Очевидно, что верхний полуэллипс задается с помощью функции вида y = 5 + 5 2 4 — x — 3 2 , а нижний y = 5 — 5 2 4 — x — 3 2 .
Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2 ; 5 3 2 + 5 будет иметь вид
y ‘ = 5 + 5 2 4 — x — 3 2 ‘ = 5 2 · 1 2 4 — ( x — 3 ) 2 · 4 — ( x — 3 ) 2 ‘ = = — 5 2 · x — 3 4 — ( x — 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = — 5 2 · 2 — 3 4 — ( 2 — 3 ) 2 = 5 2 3 ⇒ y = y ‘ ( x 0 ) · x — x 0 + y 0 ⇔ y = 5 2 3 ( x — 2 ) + 5 3 2 + 5
Получаем, что уравнение второй касательной со значением в точке
2 ; — 5 3 2 + 5 принимает вид
y ‘ = 5 — 5 2 4 — ( x — 3 ) 2 ‘ = — 5 2 · 1 2 4 — ( x — 3 ) 2 · 4 — ( x — 3 ) 2 ‘ = = 5 2 · x — 3 4 — ( x — 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = 5 2 · 2 — 3 4 — ( 2 — 3 ) 2 = — 5 2 3 ⇒ y = y ‘ ( x 0 ) · x — x 0 + y 0 ⇔ y = — 5 2 3 ( x — 2 ) — 5 3 2 + 5
Графически касательные обозначаются так:
Касательная к гиперболе
Когда гипербола имеет центр в точке x c e n t e r ; y c e n t e r и вершины x c e n t e r + α ; y c e n t e r и x c e n t e r — α ; y c e n t e r , имеет место задание неравенства x — x c e n t e r 2 α 2 — y — y c e n t e r 2 b 2 = 1 , если с вершинами x c e n t e r ; y c e n t e r + b и x c e n t e r ; y c e n t e r — b , тогда задается при помощи неравенства x — x c e n t e r 2 α 2 — y — y c e n t e r 2 b 2 = — 1 .
Гипербола может быть представлена в виде двух объединенных функций вида
y = b a · ( x — x c e n t e r ) 2 — a 2 + y c e n t e r y = — b a · ( x — x c e n t e r ) 2 — a 2 + y c e n t e r или y = b a · ( x — x c e n t e r ) 2 + a 2 + y c e n t e r y = — b a · ( x — x c e n t e r ) 2 + a 2 + y c e n t e r
В первом случае имеем, что касательные параллельны о у , а во втором параллельны о х .
Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.
Составить уравнение касательной к гиперболе x — 3 2 4 — y + 3 2 9 = 1 в точке 7 ; — 3 3 — 3 .
Решение
Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что
x — 3 2 4 — y + 3 2 9 = 1 ⇒ y + 3 2 9 = x — 3 2 4 — 1 ⇒ y + 3 2 = 9 · x — 3 2 4 — 1 ⇒ y + 3 = 3 2 · x — 3 2 — 4 и л и y + 3 = — 3 2 · x — 3 2 — 4 ⇒ y = 3 2 · x — 3 2 — 4 — 3 y = — 3 2 · x — 3 2 — 4 — 3
Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7 ; — 3 3 — 3 .
Очевидно, что для проверки первой функции необходимо y ( 7 ) = 3 2 · ( 7 — 3 ) 2 — 4 — 3 = 3 3 — 3 ≠ — 3 3 — 3 , тогда точка графику не принадлежит, так как равенство не выполняется.
Для второй функции имеем, что y ( 7 ) = — 3 2 · ( 7 — 3 ) 2 — 4 — 3 = — 3 3 — 3 ≠ — 3 3 — 3 , значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.
y ‘ = — 3 2 · ( x — 3 ) 2 — 4 — 3 ‘ = — 3 2 · x — 3 ( x — 3 ) 2 — 4 ⇒ k x = y ‘ ( x 0 ) = — 3 2 · x 0 — 3 x 0 — 3 2 — 4 x 0 = 7 = — 3 2 · 7 — 3 7 — 3 2 — 4 = — 3
Ответ: уравнение касательной можно представить как
y = — 3 · x — 7 — 3 3 — 3 = — 3 · x + 4 3 — 3
Наглядно изображается так:
Касательная к параболе
Чтобы составить уравнение касательной к параболе y = a x 2 + b x + c в точке x 0 , y ( x 0 ) , необходимо использовать стандартный алгоритм, тогда уравнение примет вид y = y ‘ ( x 0 ) · x — x 0 + y ( x 0 ) . Такая касательная в вершине параллельна о х .
Следует задать параболу x = a y 2 + b y + c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у . Получаем, что
x = a y 2 + b y + c ⇔ a y 2 + b y + c — x = 0 D = b 2 — 4 a ( c — x ) y = — b + b 2 — 4 a ( c — x ) 2 a y = — b — b 2 — 4 a ( c — x ) 2 a
Графически изобразим как:
Для выяснения принадлежности точки x 0 , y ( x 0 ) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна о у относительно параболы.
Написать уравнение касательной к графику x — 2 y 2 — 5 y + 3 , когда имеем угол наклона касательной 150 ° .
Решение
Начинаем решение с представления параболы в качестве двух функций. Получим, что
— 2 y 2 — 5 y + 3 — x = 0 D = ( — 5 ) 2 — 4 · ( — 2 ) · ( 3 — x ) = 49 — 8 x y = 5 + 49 — 8 x — 4 y = 5 — 49 — 8 x — 4
Значение углового коэффициента равняется значению производной в точке x 0 этой функции и равняется тангенсу угла наклона.
k x = y ‘ ( x 0 ) = t g α x = t g 150 ° = — 1 3
Отсюда определим значение х для точек касания.
Первая функция запишется как
y ‘ = 5 + 49 — 8 x — 4 ‘ = 1 49 — 8 x ⇒ y ‘ ( x 0 ) = 1 49 — 8 x 0 = — 1 3 ⇔ 49 — 8 x 0 = — 3
Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150 ° для такой функции не существует.
Вторая функция запишется как
y ‘ = 5 — 49 — 8 x — 4 ‘ = — 1 49 — 8 x ⇒ y ‘ ( x 0 ) = — 1 49 — 8 x 0 = — 1 3 ⇔ 49 — 8 x 0 = — 3 x 0 = 23 4 ⇒ y ( x 0 ) = 5 — 49 — 8 · 23 4 — 4 = — 5 + 3 4
Имеем, что точки касания — 23 4 ; — 5 + 3 4 .
Ответ: уравнение касательной принимает вид
Видео:Дан график производной Найти абсциссу точки в которой касательная к графику функции парал-на оси ХСкачать

Решение задач на геометрический смысл производной — справочник студента
Геометрический смысл производной. Решение задач из ЕГЭ.
- Автор презентации: Белякова Ольга Владимировна,
- учитель математики МОУ «ЛСОШ №2»
- г. Лихославль Тверской области
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой х 0 . Найдите значение производной функции f(x) в точке х 0 .
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой х 0 . Найдите значение производной функции f(x) в точке х 0 .
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой х 0 . Найдите значение производной функции f(x) в точке х 0 .
На рисунке изображен график функции y=f `(x) – производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y=f(x) параллельна оси абсцисс или совпадает с ней.
Касательная к графику y=f(x) параллельна оси абсцисс или совпадает с ней в точке с абсциссой, которая удовлетворяет условию f `(x 0 )=0. Значит следует искать точку пересечения данного графика производной с осью абсцисс. По рисунку х 0 =4.
На рисунке изображен график функции y=f (x), определенной на интервале (-6;5). Найдите количество точек, в которых касательная к графику функции параллельна прямой у=-8.
Прямая у=-8 параллельна оси абсцисс. Касательная к графику функции y=f (x) будет параллельна оси абсцисс в точках минимума и максимума функции. Таких точек на рисунке – 6.
На рисунке изображен график y=f `(x) – производной функции f(x), определенной на интервале (-1;12). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой у=2х-15 или совпадает с ней.
Касательная к графику функции f(x) должна быть параллельна прямой у=2х-15, то есть угловой коэффициент касательной должен быть равен 2. (k=2) k=f `(x 0 ). Следовательно, f `(x 0 )=2. Находим на графике производной точки, в которых значение функции (производной) равно 2. Таких точек на рисунке 3.
На рисунке изображен график y=f `(x) – производной функции f(x), определенной на интервале (-9;8). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой у=2х+5 или совпадает с ней.
Касательная к графику функции f(x) должна быть параллельна прямой у=2х+5, то есть угловой коэффициент касательной должен быть равен 2. (k=2) k=f `(x 0 ). Следовательно, f `(x 0 )=2. Находим на графике производной точки, в которых значение функции (производной) равно 2. Таких точек на рисунке 4.
На рисунке изображен график y=f `(x) – производной функции f(x), определенной на интервале (-8;5). В какой точке отрезка [-3;2] f(x) принимает наибольшее значение?
На отрезке [-3;2] производная принимает только отрицательные значения. Значит, на этом отрезке функция f(x) – убывает. Следовательно, на левом конце отрезка (в точке -3) значение функции – наибольшее, а на правом конце отрезка (в точке 2) значение функции – наименьшее.
На рисунке изображен график y=f `(x) – производной функции f(x), определенной на интервале (-2;9). В какой точке отрезка [1;5] f(x) принимает наименьшее значение?
На отрезке [1;5] производная принимает только положительные значения. Значит, на этом отрезке функция f(x) – возрастает. Следовательно, на левом конце отрезка (в точке 1) значение функции – наименьшее, а на правом конце отрезка (в точке 5) значение функции – наибольшее.
- №10
- На рисунке изображен график
- y=f `(x) – производной функции f(x), определенной на интервале
(-2;18). Найдите количество точек минимума функции f(x) на отрезке [0;15].
В точках экстремума функции (минимума и максимума) производная равна нулю. Следовательно, нужно найти точки пересечения графика производной с осью абсцисс. Таких точек (попадающих на отрезок [0;15]) на рисунке – 3. В точке минимума производная меняет знак с «-» на «+». На рисунке это выполняется для двух точек.
- №11
- На рисунке изображен график
- y=f `(x) – производной функции f(x), определенной на интервале
(-3;11). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
На промежутке убывания функции f(x), ее производная отрицательна. На рисунке есть два промежутка, на которых производная функции принимает отрицательные значения. Это отрезки [-2;2] и [6;10] . Длина первого отрезка=2-(-2)=4. Длина второго отрезка=10-6=4. Длины обоих отрезков одинаковы.
- №12
- На рисунке изображен график
- y=f `(x) – производной функции f(x), определенной на интервале
(-2;11). Найдите точку экстремума функции f(x) на отрезке [0;5].
В точках экстремума функции (минимума и максимума) производная равна нулю. Следовательно, нужно найти точки пересечения графика производной с осью абсцисс. Такая точка (при этом принадлежащая отрезку [0;5]) на рисунке только одна. Это точка х= 3.
Видео:ЕГЭ 2017 Профильный №7 найти точки, в которых касательная параллельна прямой #7Скачать

Обучающие карточки «Геометрический смысл производной»
Обучающие карточки по алгебре.
Геометрический смысл производной.



| На рисунке изображён график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке . | |
| 1 | 4 |
| 2 | 5 |
| 3 | 6 |
| На рисунке изображён график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке . | |
| 7 | 10 |
| 8 | 11 |
| 9 | 12 |
| На рисунке изображён график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке . | |
| 13 | 17 |
| 14 | 18 |
| 15 | 19 |
| 16 | 20 |
| На рисунке изображён график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке . | |
| 21 | 25 |
| 22 | 26 |
| 23 | 27 |
| 24 | 28 |
| 1 | На рисунке изображен график функции, определенной на интервале Найдите количество точек, в которых касательная к графику функции параллельна прямой |
| 2 | На рисунке изображен график функции ,определенной на интервале Найдите количество точек, в которых касательная к графику функции параллельна прямой |
| 3 | На рисунке изображен график функции , определенной на интервале Найдите количество точек, в которых касательная к графику функции параллельна прямой |
| 4 | На рисунке изображен график функции, определенной на интервале Найдите количество точек, в которых касательная к графику функции параллельна прямой |
| 5 | На рисунке изображен график функции , определенной на интервале Найдите количество точек, в которых касательная к графику функции параллельна прямой |
| 6 | На рисунке изображен график функции , определенной на интервале Найдите количество точек, в которых касательная к графику функции параллельна прямой |
| 7 | На рисунке изображен график функции , определенной на интервале Найдите количество точек, в которых касательная к графику функции параллельна прямой |
| 8 | На рисунке изображен график функции , определенной на интервале Найдите количество точек, в которых касательная к графику функции параллельна прямой |
| 1 | На рисунке изображен график производной функции , определенной на интервале Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней. |
| 2 | На рисунке изображен график производной функции , определенной на интервале Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней. |
| 3 | На рисунке изображен график производной функции , определенной на интервале Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней. |
| 4 | На рисунке изображен график производной функции , определенной на интервале Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней. |
| 5 | На рисунке изображен график производной функции , определенной на интервале Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней. |
| 6 | На рисунке изображен график производной функции , определенной на интервале Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней. |
| 7 | На рисунке изображен график производной функции , определенной на интервале Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней. |
| 8 | На рисунке изображен график производной функции , определенной на интервале Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней. |
| На рисунке изображён график функции, к которому проведены касательные в четырёх точках. Пользуясь графиком, поставьте в соответствие каждой точке значение производной в ней. | |||||
| 1 |
| ||||
| 2 |
| ||||
| 3 |
| ||||
| 4 |
|
| Каждому из четырёх графиков функций в первом перечне соответствует одно из значений производной функции в точке во втором перечне. Установите соответствие между графиками и значениями производной. | ||
| 1 | ГРАФИКИ |
|
| 2 | ГРАФИКИ |
|
| 3 | ГРАФИКИ |
|
Самостоятельная работа. Геометрический смысл производной
| На рисунке изображён график функции, к которому проведены касательные в четырёх точках. Пользуясь графиком, поставьте в соответствие каждой точке значение производной в ней. | |||||
| 1 |
| ||||
| На рисунке изображён график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке . | |||||
| 2 | А) | Б) | |||
| 3 | На рисунке изображен график функции , определенной на интервале Найдите количество точек, в которых касательная к графику функции параллельна прямой | ||||
| 4 | На рисунке изображен график производной функции , определенной на интервале Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней. |
Самостоятельная работа. Геометрический смысл производной
| На рисунке изображён график функции, к которому проведены касательные в четырёх точках. Пользуясь графиком, поставьте в соответствие каждой точке значение производной в ней. | ||||||
| 1 |
| |||||
| На рисунке изображён график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке . | ||||||
| 2 | А) | Б) | ||||
| 3 | На рисунке изображен график функции , определенной на интервале Найдите количество точек, в которых касательная к графику функции параллельна прямой | |||||
| 4 | На рисунке изображен график производной функции , определенной на интервале Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней. |
| 5 | На рисунке изображен график функции y=f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 10. Найдите f ‘(10). | |
| Каждому из четырёх графиков функций в первом перечне соответствует одно из значений производной функции в точке во втором перечне. Установите соответствие между графиками и значениями производной. | ||
| 6 | ГРАФИКИ |
|
| 5 | На рисунке изображен график функции y=f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 8. Найдите f ‘(8). | |
| Каждому из четырёх графиков функций в первом перечне соответствует одно из значений производной функции в точке во втором перечне. Установите соответствие между графиками и значениями производной. | ||
| 6 | ГРАФИКИ |
|
Видео:Математика без Ху!ни. Уравнение касательной.Скачать

Геометрический смысл производной
Параллельно с Ньютоном, который исследовал физические процессы и пришёл к пониманию о производной своим путём, Лейбниц ввёл определение производной через геометрию.
Для того чтобы разобраться в чём заключается геометрический смысл производной, обратимся к вышеприведённому схематическому рисунку. На нём изображён график функции y=f(x).
Обозначим через P точку, которой соответствует значение функции в точке x0.
Проведём некоторую секущую через точки P и P1. Угол наклона между положительным направлением оси X и этой секущей обозначим через β.
В результате получился прямоугольный треугольник с катетами Δx и Δy. Здесь Δx — это приращение аргумента функции, а Δy — приращение самой функции.
Отношение приращения функции к приращению аргумента есть тангенс угла между секущей и положительным направлением оси абсцисс.
Если устремить Δx→0, то точка P1 на графике будет приближаться к точке P, а секущая — менять своё положение относительно графика.
Предельным положением секущей при стремящемся к нулю приращению будет прямая, в которой точки P и P1 совпадут друг с другом. Такая прямая называется касательной к графику в точке P.
● Геометрический смысл производной заключается в том, что значение производной функции в точке численно равно тангенсу угла наклона касательной к функции в этой точке.
Известно, что уравнение любой прямой имеет такой общий вид: y=k*x+b. Так вот в уравнении касательной к функции в точке P коэффициент k как раз равен значению производной в точке x0
На практике часто встречаются задачи на применение геометрического смысла производной. Например, одна из таких задач — это исследование графика функции по заданному графику производной от этой функции.
Прикладные задачи на производную зачастую связаны с физическим понятием производной
Видео:Касательная к графику функции в точке. 10 класс.Скачать

Геометрический смысл производной
Прямая (y = kx + b) касается графика функции (y = f(x)) в точке ((x_0; f(x_0))), если она проходит через эту точку и (f'(x_0) = k).
Угловой коэффициент прямой (y = kx + b) – это число (k).
Угол наклона прямой (y = kx + b) – это угол между этой прямой и положительным направлением оси (Ox), отсчитываемый в направлении против часовой стрелки. Таким образом, угол наклона прямой лежит в полуинтервале ([0^circ; 180^circ)).
Пример
- Утверждение
- Угловой коэффициент прямой (y=kx+b) равен тангенсу угла её наклона: [k=mathrm,alpha]
- Таким образом, угловой коэффициент касательной (y_k) к графику функции (y = f(x)) в точке ((x_0; f(x_0))) равен тангенсу угла наклона этой касательной.
- Утверждение
- Угловой коэффициент касательной (y_k=kx+b) к графику функции (y = f(x)) в точке ((x_0; f(x_0))) равен значению производной этой функции (f'(x)), взятому в точке (x_0): [k=f'(x_0)]
Если вы планируете сдавать профильную математику и рассчитываете на конкурентные баллы, вам обязательно нужно уметь находить геометрический смысл производной в ЕГЭ.
Подобные задания включены в аттестационное испытание, поскольку позволяют оценить, насколько будущий выпускник умеет работать с научным текстом, анализировать и систематизировать информацию.
Задачи на нахождение геометрического смысла производной в ЕГЭ также выявляют уровень развития логического мышления учащегося.
Как подготовиться к экзамену?
Для того чтобы задания в ЕГЭ на тему «Геометрический смысл производной» не доставляли вам неудобств, воспользуйтесь при подготовке к выпускному испытанию образовательным ресурсом «Школково». С нами вы сможете повторить теоретический материал по темам, которые вызывают у вас трудности. Теоремы и формулы, которые раньше казались вам сложными, изложены доступно и понятно.
Каждое упражнение содержит правильный ответ и подробный ход решения. Вы можете выполнять задания различного уровня сложности. Школьник, проживающий в Москве и любом другом населенном пункте, который готовится к сдаче ЕГЭ, сможет решить задачи на нахождение геометрического смысла производной, сохранить их в «Избранном», а потом обсудить со своим учителем или репетитором.
Видео:ЕГЭ по математике. Профильный уровень. Задание 7. Производная функции. КасательнаяСкачать

Самая удобная и увлекательная подготовка к ЕГЭ
- Производной функции $y = f(x)$ в данной точке $х_0$ называют предел отношения приращения функции к соответствующему приращению его аргумента при условии, что последнее стремится к нулю:
- $f'(x_0)=↙/$
- Дифференцированием называют операцию нахождения производной.
Таблица производных некоторых элементарных функций
| Функция | Производная |
| $c$ | $0$ |
| $x$ | $1$ |
| $x^n$ | $nx^$ |
| $/$ | $-/$ |
| $√x$ | $/$ |
| $e^x$ | $e^x$ |
| $lnx$ | $/$ |
| $sinx$ | $cosx$ |
| $cosx$ | $-sinx$ |
| $tgx$ | $/$ |
| $ctgx$ | $-/$ |
Основные правила дифференцирования
1. Производная суммы (разности) равна сумме (разности) производных
- Найти производную функции $f(x)=3x^5-cosx+/$
- Производная суммы (разности) равна сумме (разности) производных.
- $f'(x) = (3x^5 )’-(cos x)’ + (/)’ = 15x^4 + sinx — /$
2. Производная произведения
Найти производную $f(x)=4x·cosx$
3. Производная частного
4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции
Физический смысл производной
Если материальная точка движется прямолинейно и ее координата изменяется в зависимости от времени по закону $x(t)$, то мгновенная скорость данной точки равна производной функции.
Точка движется по координатной прямой согласно закону $x(t)= 1,5t^2-3t + 7$, где $x(t)$ — координата в момент времени $t$. В какой момент времени скорость точки будет равна $12$?
- Решение:
- 1. Скорость – это производная от $x(t)$, поэтому найдем производную заданной функции
- $v(t) = x'(t) = 1,5·2t -3 = 3t -3$
- 2. Чтобы найти, в какой момент времени $t$ скорость была равна $12$, составим и решим уравнение:
- $3t-3 = 12$
- $3t = 15$
- $t = 5$
- Ответ: $5$
Геометрический смысл производной
Напомним, что уравнение прямой, не параллельной осям координат, можно записать в виде $y = kx + b$, где $k$ – угловой коэффициент прямой. Коэффициент $k$ равен тангенсу угла наклона между прямой и положительным направлением оси $Ох$.
- $k = tgα$
- Производная функции $f(x)$ в точке $х_0$ равна угловому коэффициенту $k$ касательной к графику в данной точке:
- $f'(x_0) = k$
- Следовательно, можем составить общее равенство:
- $f'(x_0) = k = tgα$
На рисунке касательная к функции $f(x)$ возрастает, следовательно, коэффициент $k > 0$. Так как $k > 0$, то $f'(x_0) = tgα > 0$. Угол $α$ между касательной и положительным направлением $Ох$ острый.
На рисунке касательная к функции $f(x)$ убывает, следовательно, коэффициент $k 0$
Для того, чтобы найти $f'(x_0)$, найдем тангенс угла наклона между касательной и положительным направлением оси $Ох$. Для этого достроим касательную до треугольника $АВС$.
Найдем тангенс угла $ВАС$. (Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему катету.)
- $tg BAC = / = /= /=0,25$
- $f'(x_0) = tg ВАС = 0,25$
- Ответ: $0,25$
- Производная так же применяется для нахождения промежутков возрастания и убывания функции:
- Если $f'(x) > 0$ на промежутке, то функция $f(x)$ возрастает на этом промежутке.
- Если $f'(x) https://examer.ru/ege_po_matematike/teoriya/issledovanie_funkcii
Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать
Геометрический смысл производной в заданиях КИМ ЕГЭ. — презентация
- 1 Геометрический смысл производной в заданиях КИМ ЕГЭ
- 2 х y 0 k – угловой коэффициент прямой (касательной) Касательная Геометрический смысл производной Производная от функции в данной точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.
- 3 х 2 х 3 х 4 х у В точке х 2 угол наклона касательной – острый, значит, В точке х 4 угол наклона касательной – тупой, значит, В точке х 3 угол наклона касательной – равен 0°, значит,
- 4 0 у х 1 1 Показать (2) — 3 х 1 0 х В Укажите абсциссу точки, в которой касательная к графику функции y = f (x) имеет наименьший угловой коэффициент
- 5 Ищу наименьше значение производной Показать (2) 3 х 1 0 х В 5 —
6 0 У Х 1 1 Показать (2) Так как k = f ´(x o ) = 2, то считаю точки, в которых производная принимает значения 2 Ответ: 2 К графику функции y = f (x) провели все касательные, параллельные прямой у = 2 х + 5 (или совпадающие с ней). Укажите количество точек касания.
7 — 3 х 1 0 х В У Х 1 1
8 0 у х Прямая, проходящая через начало координат, касается графика функции y = f (x). Найдите производную функции в точке х = 5. y = f (x)
9 Производная функции в точке х = 5 – это производная в точке касания х о, а она равна угловому коэффициенту касательной. Рассуждение (3) — 3 х 1 0 х В 5 0, 6 3 Прямая, проходящая через начало координат, касается графика функции y = f (x). Найдите производную функции в точке х = 5. х у y = f (x)
10 0 У Х 1 1 Рассуждение (2) Ответ (2) — 3 х 1 0 х В К графику функции y = f (x) (на рисунке его нет) провели касательные под углом 135° к положительному направлению оси Ох. На рисунке изображён график производной функции. Укажите количество точек касания
📸 Видео
Производные, номер 23.1, ЕГЭ по профильной математикеСкачать
Задача 7 ЕГЭ по математике #2Скачать
Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать
Касательная к графику функции параллельна прямой y = 6Скачать
Все Задания 8 ЕГЭ 2024 ПРОФИЛЬ из Банка ФИПИ (Математика Школа Пифагора)Скачать
ЕГЭ производная |На рисунке изображен график производной функции f(x), определенной на интервале...Скачать
Прямая y=8x+11 параллельна касательной к графику функции y=x^2+7x-7. Найдите абсциссу точки касания.Скачать
Геометрический смысл производной | КасательнаяСкачать