Дано abcd пространственный четырехугольник l середина ab k середина bc n середина dc bd 70

Дано: АВСD-пространственный четырехугольник.

Рассмотрим треугольник АВС:

М-середина АВ, N-середина ВС

Значит, MN-средняя линия треугольника АВС.

Рассмотрим треугольник АDC:

Треугольники ADC и DEK- подобные (по второму признаку подобия треугольников), т.к угол D-общий, а его стороны пропорциональны:

Если угол одного треугольника равен углу другого, а стороны, образующие тот угол в одном треугольнике, пропорциональны соответствующим сторонам другого, то такие треугольники подобны.

А так как два эти треугольника подобны, то КЕ||AC

Так как KE||AC, MN||AC => KE||MN.

По определению трапеции, четырехугольник называется трапецией, если две его стороны параллельны, а две другие стороны не параллельны.

Докажем, что стороны КМ, EN не параллельны друг другу.

Значит, стороны KM, EN не могут быть параллельными в связи с разным отношением сторон.

Видео:№47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать

Презентация по математике на тему «Решение задач. Пространственный четырехугольник»

Видео:№131. В тетраэдре ABCD точка М — середина ребра ВС, АВ = AC, DB = DC. Докажите, что плоскостьСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Видео:№785. Точки М и N — середины диагоналей АС и BD четырехугольника ABCD.Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Пространственый четырехугольник. Решение задач. гимназия 64 учитель математики Котельникова Н. В.

Доказательство Пусть нам дан пространственный четырехугольник ABCD. M, N, K, L – середины ребер BD, AD, AC, BC соответственно. Нужно доказать, что MNKL – параллелограмм. Рассмотрим треугольник АВD. МN – средняя линия. По свойству средней линии, МN параллельна АВ и равняется ее половине. Рассмотрим треугольник АВС. LК – средняя линия. По свойству средней линии, LК параллельна АВ и равняется ее половине. И МN, и LК параллельны АВ. Значит, МN параллельна LК по теореме о трех параллельных прямых. Получаем, что в четырехугольнике MNKL – стороны МN и LК параллельны и равны, так как МN и LК равны половине АВ. Значит, по признаку параллелограмма, четырехугольник MNKL – параллелограмм, что и требовалось доказать.

Четырехугольник называется пространственным, если его вершины не лежат в одной плоскости. № 1.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 938 человек из 79 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 697 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 334 человека из 73 регионов

Ищем педагогов в команду «Инфоурок»

• Котельникова Наталья ВячеславовнаНаписать 4706 07.01.2019

Номер материала: ДБ-345782

07.01.2019 235

07.01.2019 135

07.01.2019 169

07.01.2019 216

07.01.2019 245

05.01.2019 83

30.12.2018 404

29.12.2018 174

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Детский омбудсмен предложила ужесточить наказание за преступления против детей

Время чтения: 1 минута

Минпросвещения готовит рекомендации по построению «идеальной школы»

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:№73. В тетраэдре ABCD точки М, N и Р являются серединами ребер АВ, ВС и CD, АС=10 см, BD= 12 смСкачать

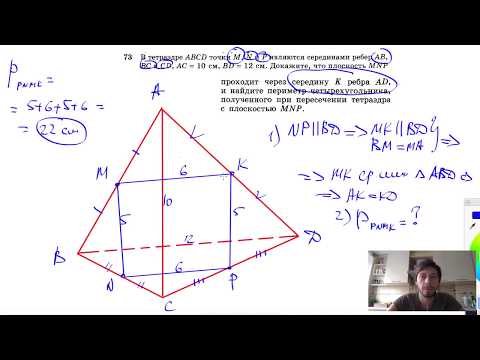
. Дан пространственный четырехугольникАВСD, М и N середины сторон АВи

. Дан пространственный четырехугольникАВСD, М и N середины сторон АВи ВСсоответственно; Е CD, K DA, DE : EC = 1 : 2, DK : KA = 1 : 2.

а) Сделайте рисунок к задачке.

б) Обоснуйте, что четырехугольникMNEK есть трапеция.

• Васька Журули
• Геометрия 2019-08-08 13:45:46 7 1

Дано: АВСD-пространственный четырехугольник.

Рассмотрим треугольник АВС:

М-середина АВ, N-середина ВС

Означает, MN-средняя линия треугольника АВС.

Рассмотрим треугольник АDC:

Треугольники ADC и DEK- сходственные (по второму признаку подобия треугольников), т.к угол D-общий, а его стороны пропорциональны:

Если угол 1-го треугольника равен углу иного, а стороны, образующие тот угол в одном треугольнике, пропорциональны подходящим сторонам иного, то такие треугольники сходственны.

А так как два эти треугольника подобны, то КЕAC

Так как KEAC, MNAC =gt; KEMN.

По определению трапеции, четырехугольник именуется трапецией, если две его стороны параллельны, а две иные стороны не параллельны.

Докажем, что стороны КМ, EN не параллельны друг другу.

Означает, стороны KM, EN не могут быть параллельными в связи с различным отношением сторон.

📹 Видео

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Как строить сечения параллелепипедаСкачать

№17. На рисунке 17 точки М, N, Q и Р — середины отрезков DB, DC, АС и АВ.Скачать

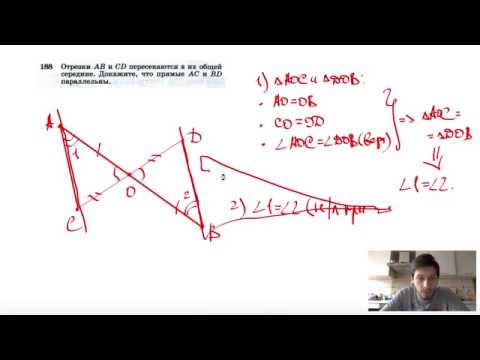
№188. Отрезки АВ и CD пересекаются в их общей середине. Докажите, что прямые АССкачать

№158. Через вершину В ромба ABCD проведена прямая ВМ, перпендикулярная к его плоскости. НайдитеСкачать

Профильный ЕГЭ 2023. Задача 13. Построение сечений. Стереометрия. 10 классСкачать

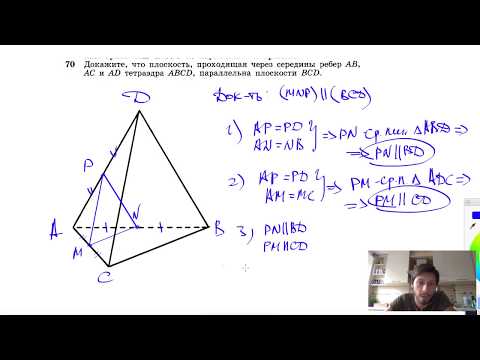
№70. Докажите, что плоскость, проходящая через середины ребер АВ, АС и AD тетраэдра ABCD,Скачать

№320. В тетраэдре ABCD точки М, N и К— середины ребер АС. ВС и CD соответственноСкачать

10 класс, 12 урок, ТетраэдрСкачать

3 правила для вписанного четырехугольника #shortsСкачать

Как строить сечения тетраэдра и пирамидыСкачать

2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать

№384. Через середину М стороны АВ треугольника ABC проведена прямая,Скачать

Задача 16. (Планиметрия) Математика профильСкачать