Сумма векторов ab ac

Теорема 1 От любой точки ( K ) можно отложить вектор единственный ( overrightarrow ) .

Существование: Имеем два следующих случая:

Здесь получаем, что искомый нами вектор совпадает с вектором ( overrightarrow ) .

Из данного выше построения сразу же будет следовать единственность данного вектора.

Сумма векторов. Сложение векторов. Правило треугольника

Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.

Суммой нескольких векторов ( vec ) , ( vec ) , ( vec,;ldots ) называется вектор ( vec ) , получающийся в результате последовательного сложения данных векторов.

Такая операция выполняется по правилу многоугольника.

Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
( vec + vec = left( <+ , + , + > right) )

Отметим несколько свойств сложения двух векторов:

Для произвольного вектора ( overrightarrow ) выполняется равенство

Для произвольных точек ( A, B и C ) справедливо следующее равенство

Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.

Разность векторов. Вычитание векторов

Разность двух одинаковых векторов равна нулевому вектору :
( vec — vec = vec )

Длина нулевого вектора равна нулю:
( left| vec right| = 0 )

Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
( vec — vec = left( <- , — , — > right) )

Умножение вектора на число

Пусть нам дан вектор ( overrightarrow ) и действительное число ( k ) .

Определение Произведением вектора ( overrightarrow ) на действительное число ( k ) называется вектор ( overrightarrow ) удовлетворяющий следующим условиям:

Длина вектора ( overrightarrow ) равна ( left|overrightarrowright|=left|kright||overrightarrow| ) ;

Векторы ( overrightarrow ) и ( overrightarrow ) сонаправлены, при ( kge 0 ) и противоположно направлены, если ( kle 0 )

Обозначение: ( overrightarrow=koverrightarrow ) .

Сложение и вычитание векторов

Формулы сложения и вычитания векторов

Формулы сложения и вычитания векторов для плоских задач

В случае плоской задачи сумму и разность векторов a = < a_x ; a_y > и b = < b_x ; b_y > можно найти, воспользовавшись следующими формулами:

Формулы сложения и вычитания векторов для пространчтвенных задач

В случае пространственной задачи сумму и разность векторов a = < a_x ; a_y ; a_z > и b = < b_x ; b_y ; b_z > можно найти, воспользовавшись следующими формулами:

Формулы сложения и вычитания n -мерных векторов

В случае n -мерного пространства сумму и разность векторов a = < a ₁ ; a ₂ ; . ; a_n > и b = < b ₁ ; b ₂ ; . ; b_n > можно найти, воспользовавшись следующими формулами:

Примеры задач на сложение и вычитание векторов

Примеры плоских задач на сложение и вычитание векторов

Примеры пространственных задач на сложение и вычитание векторов

Примеры задач на сложение и вычитание векторов с размерностью большей 3

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Сложение векторов. Как найти сумму векторов

Вы будете перенаправлены на Автор24

Откладывание вектора от данной точки

Для того, чтобы ввести сумму векторов, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.

Введем следующую теорему:

От любой точки $K$ можно отложить вектор $overrightarrow$ и притом только один.

Доказательство.

Существование: Здесь нужно рассмотреть два случая:

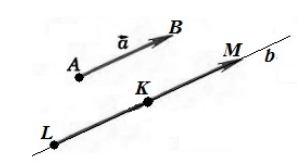
В этом случае, очевидно, что искомый вектор — вектор $overrightarrow$.

Рисунок 2. Иллюстрация теоремы 1

Единственность: единственность сразу следует из построения, проведенного в пункте «существование».

Теорема доказана.

Сложение векторов. Правило треугольника

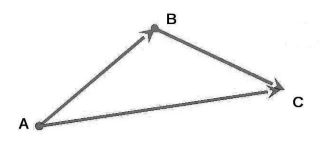
Пусть нам даны векторы $overrightarrow$ и $overrightarrow$.

Рисунок 3. Сумма векторов

Готовые работы на аналогичную тему

Иначе, определение 2, еще называют правилом треугольника для сложения двух векторов.

Из этого правила следует несколько свойств сложения двух векторов:

Для любого вектора $overrightarrow$ выполняется равенство

Для любых произвольных точек $A, B и C$ выполняется равенство

Аналогично правилу треугольника можно строить сумму любого количества векторов. Такое правило сложения называется правилом многоугольника.

Правило параллелограмма

Помимо правила треугольника для сложения двух векторов, есть еще правило параллелограмма для сложения двух векторов. Сформулируем и докажем для начала следующую теорему.

Доказательство.

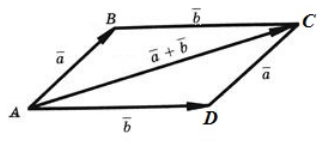
Переместительный закон:

Рисунок 4. Иллюстрация переместительного закона

Тогда выполнение переместительно закона будет очевидно вытекать из равенства длин $left|overrightarrow+overrightarrowright|и |overrightarrow+overrightarrow|$.

Сочетательный закон:

Рисунок 5. Иллюстрация сочетательного закона

Из свойства правила треугольника $overrightarrow+overrightarrow=overrightarrow$, получим:

Теорема доказана.

Пример задачи на сложение векторов

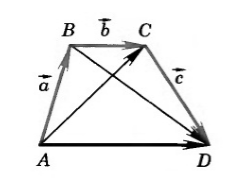
Дан четырехугольник $ABCD$. Доказать, что $overrightarrow+overrightarrow+overrightarrow=overrightarrow$

Доказательство.

Воспользуемся свойством правила треугольника $overrightarrow+overrightarrow=overrightarrow$, получим:

ч. т. д.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 01 04 2022