Дан куб abcda1b1c1d1 найти угол между векторами ad1 и bm где

Геометрия | 10 — 11 классы

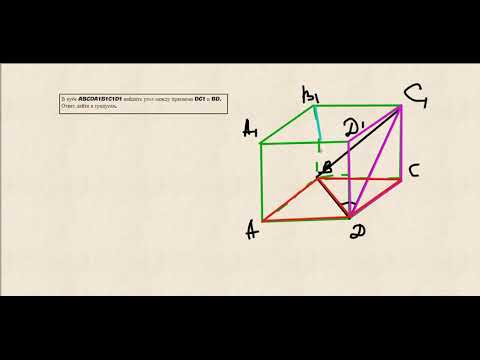
Дан куб ABCDA1B1C1D1 найдите угол между прямыми AD1 и BM, где M — середина ребра DD1 ПОЖАЛУЙСТА ОЧЕНЬ ПРОШУ.

Рассмотрим систему координат А₁В — ось ОХ, А₁Д — ось ОУ и А₁А — ось ОZ

пусть ребро куба равно «а» тогда

А₁(0, 0, 0), А ( 0, 0, а), В( а, 0, а), М ( 0, а, 0, 5а) Д₁ (0, а, 0)

1) Найдём координаты векторов АД₁( 0, а, — а) и ВМ( — а, а, — 0, 5а)

2) Найдём их длины | АД₁|² = 0² + а² + а² = 2а² тогда | АД₁| = а√2 | ВМ|² = а² + а² + 0, 25а² = 2, 25а² тогда | АД₁| = 1, 5а

3) cosα = ( 0 + а² + 0, 5а² ) / а√2 * 1, 5а = 1 / √2

тогда α = 45 градусов ( это угол между векторами).

Видео:Задание №441 — ГДЗ по геометрии 11 класс (Атанасян Л.С.)Скачать

Дан куб АВСDA1B1C1D1 с ребром а = 4 см?

Дан куб АВСDA1B1C1D1 с ребром а = 4 см.

Точки М и К – середины ребер АВ и СС1 соответственно.

Найдите : а) длину МК ; б) угол между прямыми AD1 и А1К.

Видео:№190. Дан куб ABCDA1B1C1D1. Найдите следующие двугранные углы: а) АВВ1ССкачать

ПРОВЕДИТЕ сечение куба АВСDА1В1С1D1 ПЛОСКОСТЬЮ, СОДЕРЖАЩЕГО прямую А1С1 и точку К — середину ребра ВС найдите периметр этого сечения если ребро куба ровна альфа?

ПРОВЕДИТЕ сечение куба АВСDА1В1С1D1 ПЛОСКОСТЬЮ, СОДЕРЖАЩЕГО прямую А1С1 и точку К — середину ребра ВС найдите периметр этого сечения если ребро куба ровна альфа.

Видео:В кубе ABCDA1B1C1D1 найдите угол между прямыми AD1 и В1D1. Ответ дайте в градусах.Скачать

Дана правильная четырехугольная пирамида MABCD, все ребра основания которой равны 6?

Дана правильная четырехугольная пирамида MABCD, все ребра основания которой равны 6.

Угол между прямыми DM и AL, L — середина ребра BM, равен 60.

Найти высоту пирамиды.

Видео:Как находить угол между векторамиСкачать

Дан куб ABCDA1B1C1D1?

Дан куб ABCDA1B1C1D1.

Найдите угол между прямыми AD1 и BM, где M — середина ребра DD1.

Видео:Найти в кубе угол между двумя прямымиСкачать

Дан куб abcda1b1c1d1?

Дан куб abcda1b1c1d1.

Найдите угол между прямыми Ad1 и BM, где M середина ребра DD1.

Видео:Угол между прямыми в пространстве. Практическая часть. 10 класс.Скачать

1. даны векторы а = 2i — 3j + k и b = 4i — 2k вычислите а * b2?

1. даны векторы а = 2i — 3j + k и b = 4i — 2k вычислите а * b

Дан куб ABCDA1B1D1C1 найдите угол между прямыми AD1 и BM , где М — середина ребра DD1.

Видео:Угол между векторами. 9 класс.Скачать

Дан куб ABCDA1B1C1D1?

Дан куб ABCDA1B1C1D1.

Найдите угол между прямыми AD1 и BM, где — M середина ребра DD1.

Видео:Нахождение угла между векторами через координаты. 9 класс.Скачать

В единичном кубе ABCDA1B1C1D1 найти угол между прямыми A1D и D1E, где E — середина ребра CC1?

В единичном кубе ABCDA1B1C1D1 найти угол между прямыми A1D и D1E, где E — середина ребра CC1.

Видео:100 тренировочных задач #135 Угол между векторамиСкачать

Ребро куба ABCDA1B1C1D1 равно а?

Ребро куба ABCDA1B1C1D1 равно а.

Постройте сечение куба, проходящее через прямую B1C и середину рёбра AD, и найдите площадь этого сечения.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

С рисунком, пожалуйста, натолкните на верное решение?

С рисунком, пожалуйста, натолкните на верное решение.

Ребро куба ABCDA1B1C1D1 равно a.

Постройте сечение куба , проходящее через прямую B1C и середину ребра AD, и найдите площадь этого сечения.

На этой странице находится ответ на вопрос Дан куб ABCDA1B1C1D1 найдите угол между прямыми AD1 и BM, где M — середина ребра DD1 ПОЖАЛУЙСТА ОЧЕНЬ ПРОШУ?, из категории Геометрия, соответствующий программе для 10 — 11 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Геометрия. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.

Найдём длину гипотенузы L = √(6² + 8²) = 10 см Найдём площадь прямоугольного треугольника S = ab / 2 S = 6 * 8 / 2 = 24 см² Найдём радиус описанной окружности R = abc / 4S R = 6 * 8 * 10 / 4 * 24 R = 5 см Ответ 5 см.

Т. к эти углы смежные, то в сумме они равны 180° пусть угол ABC = x, угол CBD = y. Составляем систему : x — y = 20 x + y = 180 складываем : x — y + x + y = 20 + 180 2x = 200 x = 100° y = 180 — x = 180 — 100 = 80° Ответ : угол ABC = 100°, угол CBD = ..

Все 3 медианы треугольника пересекаются в одной точке N, причем площадь каждого из шести треугольников созданного при проведении медиана равна 1 / 6 площади треугольника, соответственно Sanb = 2 * Sabc1 / 6 = 87 / 3 = 29дм².

Рассмотрим треугольники АВМ и ДСN. Т. к. АВСД — прямоугольник, то АВ = СД. Т. к. ВМ и СN — биссектрисы равных углов, то угол АВМ = ДСN. И угол А = Д по условию. Отсюда следует, что треугольник АВМ = ДСN по стороне и двум прилежащим углам. Из э..

По теореме Пифагора сумма квадратов катетов равна квадрату гипотенузы пусть один катет равен х, тогда второй равен х + 7 x ^ 2 + (x + 7) ^ 2 = 13 ^ 2 x ^ 2 + x ^ 2 + 49 + 14x = 169 2x ^ 2 + 14x — 120 = 0 x ^ 2 + 7x — 60 = 0 D = 49 + 240 = 289 x = ( -..

Сумма смежных углов — 180º (углы 1, 2 и 3, 4 — смежные). Значит, угол1 + угол 2 = 180. Но угол 1 = углу 4 поэтому можно заменить : угол4 + угол 2 = 180º. Значит, углы равны (аналогично можно проделать с углами 2 и 3).

Обозначив углы между стороной и диагоналями х и х + 30 , учитывая , что диагонали перпендикулярны , получим х + х + 30 = 90, откуда х = 30. Диагонали ромба — биссектрисы углов. Углы ромба 60 и 120.

P. S. Отметь мой ответ как лучший , спасибо : — ).

3х — (5х — (3х — 1)) = 3х — (5х — 3х — 1) = 3х — 2х — 1 = х — 1.

28 — 12 равно 16 и 16 делим на 2 равно восемь — боковая сторона.

Видео:Готовимся к ЕГЭ. Стереометрия. Базовые задачи. Угол между прямыми. КубСкачать

Дан куб abcda1b1c1d1 найти угол между векторами ad1 и bm где

Вопрос по геометрии:

дан куб ABCDA1B1C1D1 найдите угол между прямыми AD1 и BM, где M-середина ребра DD1 ПОЖАЛУЙСТА ОЧЕНЬ ПРОШУ

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Рассмотрим систему координат А₁В -ось ОХ, А₁Д -ось ОУ и А₁А- ось ОZ
пусть ребро куба равно «а» тогда
А₁(0,0,0), А ( 0,0,а), В( а,0,а), М ( 0,а, 0,5а) Д₁ (0,а,0)
1) Найдём координаты векторов
АД₁( 0,а,-а) и ВМ( -а,а, -0,5а)
2) Найдём их длины
| АД₁|² = 0²+а² +а² = 2а² тогда | АД₁| =а√2
| ВМ|² = а²+а² +0,25а² = 2,25а² тогда | АД₁| =1,5а
3) cosα = ( 0+а² +0,5а² ) / а√2*1,5а = 1/√2
тогда α =45 градусов ( это угол между векторами)

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:Задание 3 ЕГЭ профиль #121Скачать

441. Дан куб ABCDA1B1C1D1. Найдите угол между векторами: а) В1В и В1С; б) DA и B1D1; в) А1С1 и А1В; г) ВС и АС; д) ВВ1 и АС; е) В1С и AD1; ж) A1D1 и ВС; з) АА1 и С1С.

Видео:найти угол между единичными векторамиСкачать

441. Дан куб ABCDA₁B₁C₁D₁. Найдите угол между векторами: а) В₁В и В₁С; б) DA и B₁D₁; в) А₁С₁ и А₁В; г) ВС и АС; д) ВВ₁ и АС; е) В₁С и AD₁; ж) A₁D₁ и ВС; з) АА₁ и С₁С.

а) Векторы ВВ₁ и В₁С совпадают с катетом и гипотенузой прямоугольного треугольника BВ₁С, следовательно, ВВ₁С=45°.

б) BD = B₁D₁ , т.к. они сонаправлены и имеют одинаковую длину. BD = B₁D₁ =- DB .

Угол между DB и DA — угол между стороной и диагональю квадрата, т.е. α=45°. Тогда угол между

в) A₁C₁ и A₁B совпадают со сторонами равностороннего треугольника АВС и отложены из одной точки. Следовательно, угол 60°.

(угол между стороной и диагональю

Пусть О — точка пересечения диагоналей В₁С и ВС₁,

следовательно, угол между ними равен 180°

Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №441
к главе «Глава V. Метод координат в пространстве. § 2. Скалярное произведение векторов».

🌟 Видео

Решение задач (находим угол в кубе)Скачать

Урок 2. Как найти угол между прямыми || Задание №13. Стереометрия на ЕГЭСкачать

11 класс, 5 урок, Угол между векторамиСкачать

105. Угол между векторамиСкачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Угол между прямыми в пространстве. 11 класс.Скачать

№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать