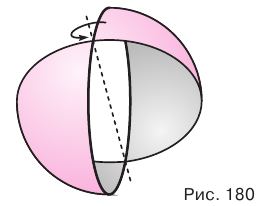
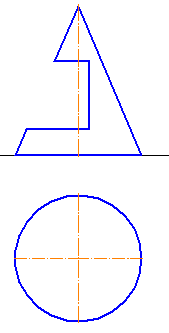
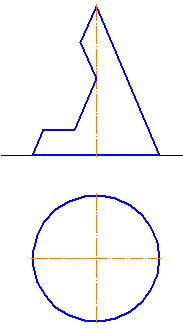
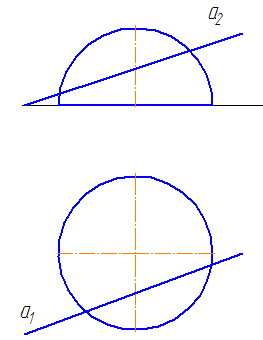
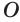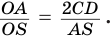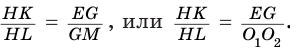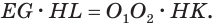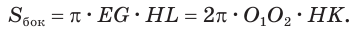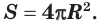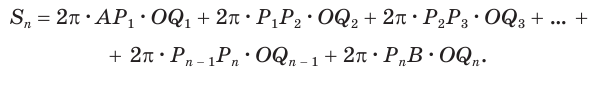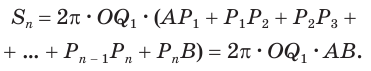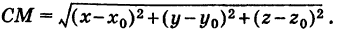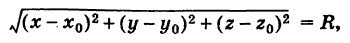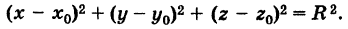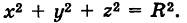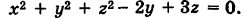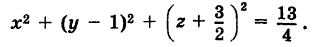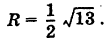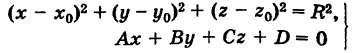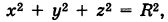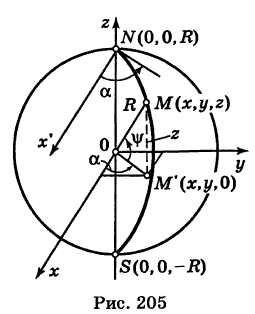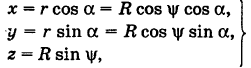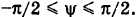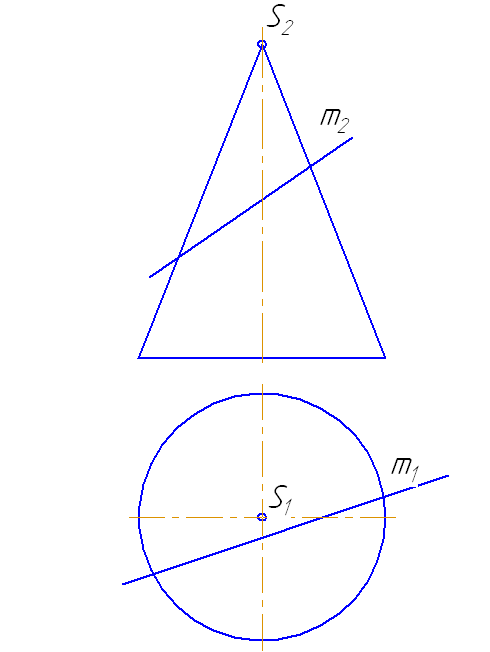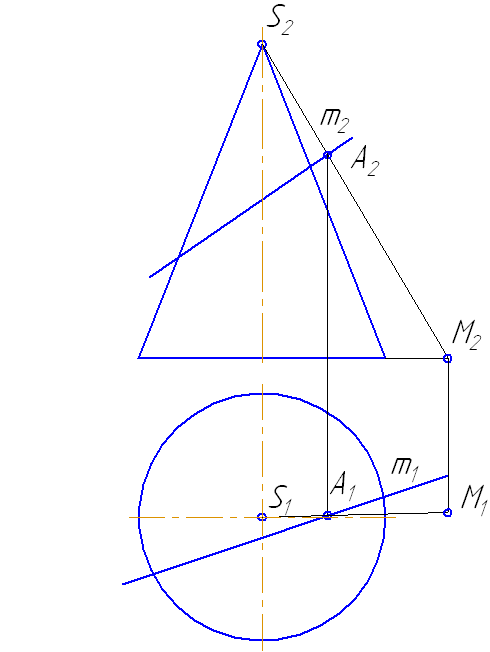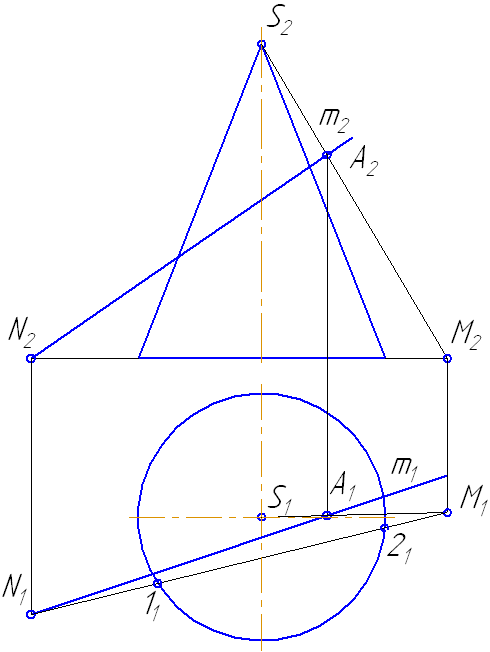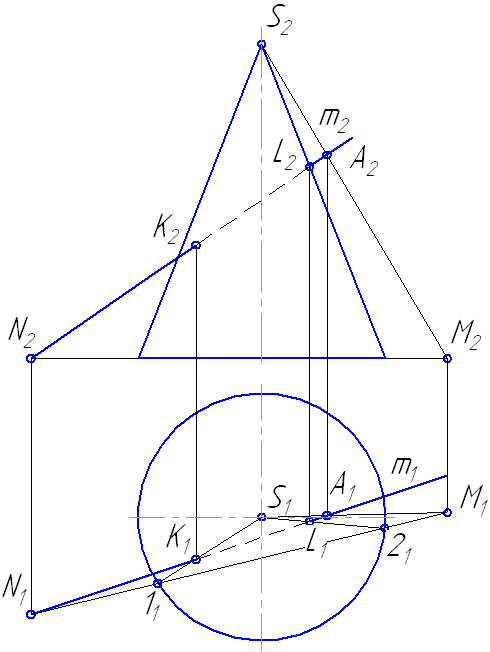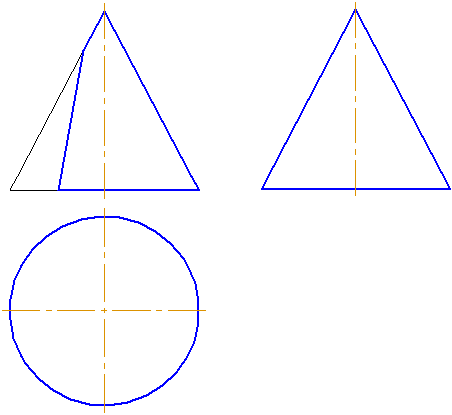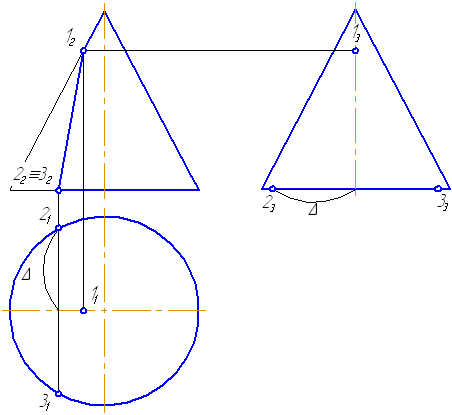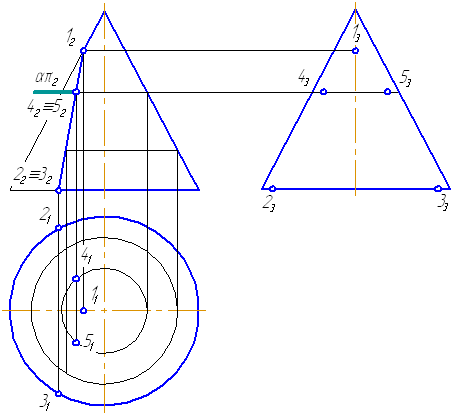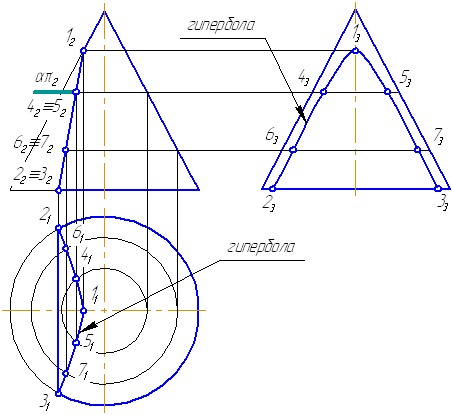Сферой называется поверхность, полученная вращением окружности вокруг какого-либо ее диаметра (рис. 180). Центр этой окружности называется центром сферы.
Отрезок, соединяющий центр сферы с любой ее точкой, называется радиусом сферы, отрезок, соединяющий две точки сферы, — хордой сферы, а хорда, которой принадлежит центр сферы, — диаметром сферы (рис. 181).
Из определения сферы следует, что все ее точки равноудалены от центра сферы. Поэтому все радиусы сферы равны друг другу.
- Теоремы
- Уравнение сферы
- Лекция 7. Поверхности
- 7.1. Поверхности. Образование и задание поверхности на чертеже
- 7.2. Поверхности вращения
- 7.3. Цилиндрическая поверхность
- 7.4. Пересечение прямой с поверхностью прямого кругового цилиндра
- Упражнение
- 7.5. Пересечение прямой с поверхностью наклонного цилиндра
- Упражнение
- 7.6. Сферическая поверхность
- Упражнение
- 7.7. Пересечение прямой с поверхностью сферы
- Упражнение
- 7.8. Коническая поверхность
- 7.9. Пересечение прямой с поверхностью конуса
- 7.10. Пересечение цилиндра плоскостью
- 7.11. Пересечение сферы плоскостью
- 7.12. Пересечение конуса плоскостью
- 7.13. Задачи для самостоятельной работы
- Урок геометрии на тему «Сфера и шар. Уравнение сферы». 11-й класс
Видео:Окружность — сфера — шарСкачать

Теоремы
Теорема 1.
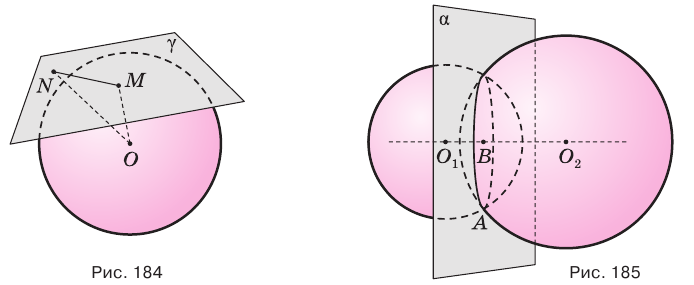
Сечение сферы плоскостью есть окружность, центр которой совпадает с основанием перпендикуляра, опущенного из центра сферы на секущую плоскость.
Доказательство:
Пусть сфера с центром
Пусть 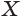
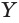
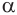
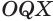
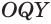
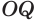
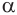
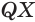
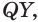
Отрезок 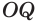
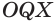
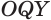
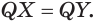
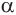


Следствие. Радиус 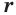
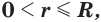
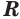
Сечение имеет наибольший радиус 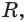
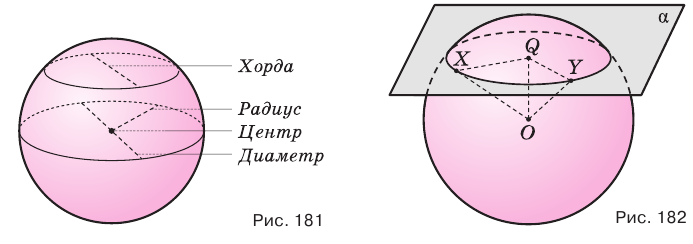
Плоскость, имеющая со сферой единственную общую точку, называется касательной плоскостью сферы. Общая точка сферы и касательной плоскости называется точкой касания.
Прямая касательной плоскости сферы, проходящая через точку касания, имеет со сферой единственную общую точку. Такая прямая называется касательной прямой сферы.
Теорема 2.
Касательная плоскость сферы перпендикулярна радиусу, проведенному в точку касания.
Доказательство:
Пусть плоскость 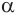
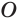

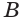
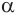

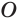

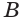
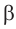
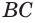

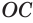
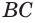
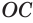
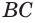

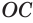
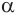
Теорема 3.
Если плоскость проходит через точку сферы и перпендикулярна радиусу, проведенному в эту точку, то она является касательной плоскостью сферы.
Доказательство:
Пусть плоскость 

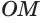
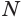


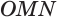
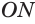
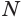





Теоремы 2 и 3 выражают соответственно свойство и признак касательной плоскости сферы.
Теорема 4.
Две сферы пересекаются по окружности, плоскость которой перпендикулярна прямой, проходящей через центры сфер.
Доказательство:
Пусть имеются две пересекающиеся сферы с центрами 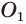
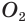
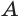
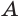
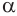
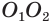
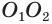

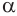


Других общих точек данные окружности не имеют. Допустим, что это не так. Пусть 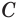

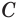
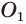
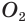
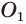
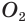

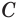
Но это противоречит утверждению о том, что две окружности имеют не более двух общих точек.
Прежде чем доказывать утверждение о поверхности сферы, обобщим утверждения о боковых поверхностях конуса, усеченного конуса и цилиндра.
Теорема 5.
Боковая поверхность конуса, усеченного конуса, цилиндра равна боковой поверхности цилиндра с той же высотой и радиусом основания, равным длине перпендикуляра, соединяющего середину образующей с точкой на оси этого тела.
Доказательство:
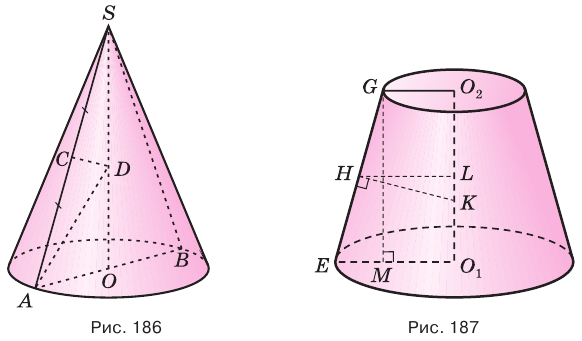
Пусть есть конус с вершиной 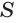
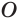
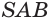
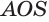
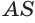
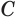
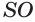
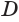
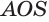
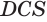
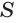
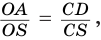
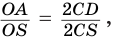
Отсюда
С учетом этого для боковой поверхности 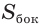
Пусть есть усеченный конус, полученный вращением прямоугольной трапеции 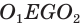
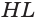
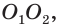
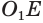
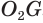
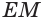
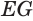
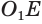
В плоскости 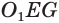
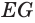
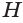
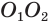
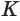
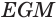
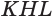
Отсюда
С учетом этого для боковой поверхности 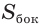
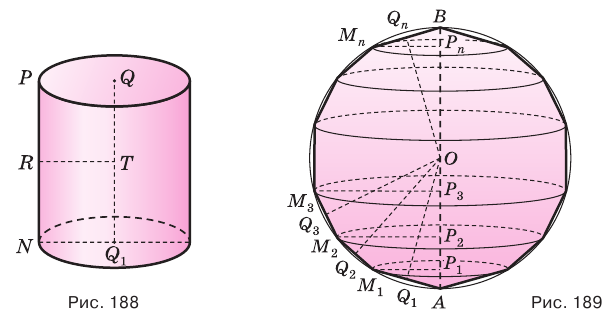
Для цилиндра утверждение очевидно (рис. 188).
Теорема 6.
Поверхность сферы равна учетверенной площади большого круга:
Доказательство:
Пусть есть сфера, образованная вращением полуокружности 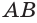
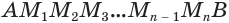
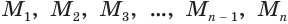
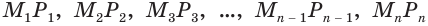
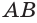


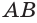
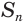
Учтем, что отрезки 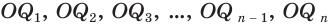
Пусть радиус сферы равен 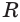
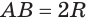
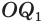
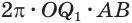
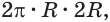
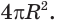
Учитывая, что 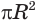
Видео:Сфера вращением окружностиСкачать

Уравнение сферы
Определение: Сферой радиуса R называется множество всех точек пространства, расстояние от каждой из которых до данной точки (центра) равно R.
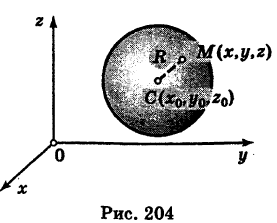
Выведем уравнение сферы. Пусть 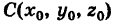
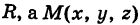
Приравнивая это выражение R, получим уравнение сферы
Если центр сферы совпадает с началом координат, то х0 = 0, у0 = 0, 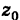
Пример:
Определить координаты центра и радиус сферы
Решение:
Объединяя члены, содержащие одноименные текущие координаты, и дополняя их до полных квадратов, будем иметь
Следовательно, центр сферы находится в точке 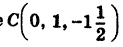
Заметим, что совокупность
уравнений сферы и плоскости определяет окружность, по которой пересекаются плоскость и сфера (если это множество не пусто). В частности, если 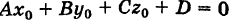
Уравнение окружности можно также писать в параметрическом виде.
Пример:
Написать параметрические уравнения меридиана сферы
проходящего через полюсы 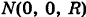
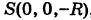
Решение:
За параметр текущей точки 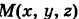
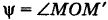
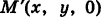
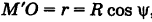
где
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
- Призма в геометрии
- Цилиндр в геометрии
- Пирамида в геометрии
- Конус в геометрии
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:11 класс, 19 урок, Сфера и шарСкачать

Лекция 7. Поверхности
Видео:Геометрия 11 класс: Сфера и шар. Уравнение сферы. Площадь сферыСкачать

7.1. Поверхности. Образование и задание поверхности на чертеже
Поверхности составляют широкое многообразие объектов трехмерного пространства. Инженерная деятельность человека связана непосредственно с проектированием, конструированием и изготовлением различных поверхностей. Большинство задач прикладной геометрии сводится к автоматизации проектно-конструкторского процесса и воспроизведения сложных поверхностей. Способы формообразования и отображения поверхностей составляют основу инструментальной базы трехмерного моделирования современных систем автоматизированного проектирования.
Рассматривая поверхности как непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением вида F(x,y,z)=0, можно выделить алгебраические поверхности (F(x,y,z)— многочлен n-ой степени и трансцендентные (F(x,y,z)— трансцендентная функция.
Если алгебраическая поверхность описывается уравнением n-й степени, то поверхность считается поверхностью n-го порядка. Произвольно расположенная секущая плоскость пересекает поверхность по кривой того же порядка (иногда распадающейся или мнимой), какой имеет исследуемая поверхность. Порядок поверхности может быть определен также числом точек её пересечения с произвольной прямой, не принадлежащей целиком поверхности, считая все точки (действительные и мнимые).
Поверхность можно рассматривать, как совокупность последовательных положений l1,l2… линии l перемещающейся в пространстве по определенному закону (Рисунок 7.1). В процессе образования поверхности линия l может оставаться неизменной или менять свою форму — изгибаться или деформироваться. Для наглядности изображения поверхности на эпюре Монжа закон перемещения линии l целесообразно задавать графически в виде одной линии или целого семейства линий (m, n, p…).
Подвижную линию принято называть образующей (li), неподвижные – направляющими (m). Такой способ образования поверхности принято называть кинематическим .
Примером такого способа могут служить все технологические процессы обработки металлов режущей кромкой, когда поверхность изделия несёт на себе «отпечаток» режущей кромки резца, т.е. её поверхность можно рассматривать как множество линий конгруэнтных профилю резца.
Рисунок 7.1 — Кинематическая поверхность
По виду образующей различают поверхности линейчатые и нелинейчатые , образующая первых – прямая линия, вторых – кривая.
Линейчатые поверхности в свою очередь разделяют на развертывающиеся , которые можно без складок и разрывов развернуть на плоскость и неразвертывающиеся .
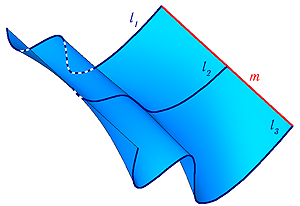
Значительный класс поверхностей формируется движением окружности постоянного или переменного радиуса. Такие поверхности носят название циклические (Рисунок 7.2).
Рисунок 7.2 — Циклическая поверхность
Если группировать поверхности по закону движения образующей линии, то большинство встречающихся в технике поверхностей можно разделить на:
- поверхности вращения;
- винтовые поверхности;
- поверхности с плоскостью параллелизма;
- поверхности параллельного переноса.
Особое место занимают такие нелинейные поверхности, образование которых, не подчинено ни какому закону. Оптимальную форму таких поверхностей определяют теми физическими условиями, в которых они работают и устанавливают форму экспериментально (поверхности лопастей турбин, обшивка каркасов морских судов и самолетов).
Для графического изображения поверхности на чертеже используется её каркас.
Множество линий, заполняющих поверхность так, что через каждую точку поверхности проходит в общем случае одна линия этого множества, называется каркасом поверхности .
Поверхность может быть задана и конечным множеством точек, которое принято называть точечным каркасом .
Проекции каркаса могут быть построены, если задан определитель поверхности – совокупность условий, задающих поверхность в пространстве и на чертеже.
Различают две части определителя: геометрическую и алгоритмическую.
Геометрическая часть определителя представляет собой набор постоянных геометрических элементов (точек, прямых, плоскостей и т.п.), которые могут и не входить в состав поверхности.
Вторая часть – алгоритмическая (описательная) – содержит перечень операций, позволяющий реализовать переход от фигуры постоянных элементов к непрерывному каркасу.
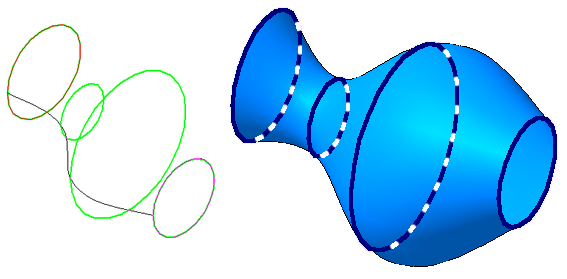
Например, циклическая поверхность, каркас которой состоит из восьмиугольников (Рисунок 7.3), может быть задан следующим образом:
- Геометрическая часть определителя: три направляющих l, m, n.
- Алгоритмическая часть: выбираем плоскость α; находим точки А, В, С, в которых α пересекает соответственно направляющие l, m, n. Строим восьмиугольник, определяемый тремя найденными точками. Переходим к следующей плоскости и повторяем построение
Рисунок 7.3 –Образование циклической поверхности
Видео:Сфера вращением двух окружностейСкачать

7.2. Поверхности вращения
Поверхностями вращения называются поверхности, полученные вращением образующей вокруг неподвижной оси (Рисунок 7.5).
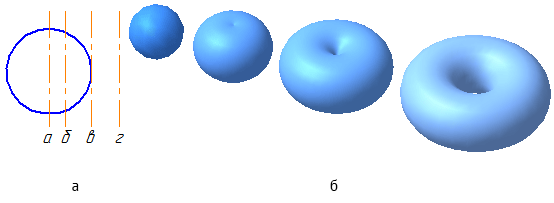
Цилиндрическая и коническая поверхности бесконечны (т.к. бесконечны образующие); сферическая, торовая поверхности — конечны.
Сферическая поверхность – частный случай торовой поверхности. При вращении окружности вокруг осей б, в, г (Рисунок 7.4, а) получим торовую поверхность (Рисунок 7.4, б), а вокруг оси а – сферическую.
Рисунок 7.4 – Образование поверхностей вращения
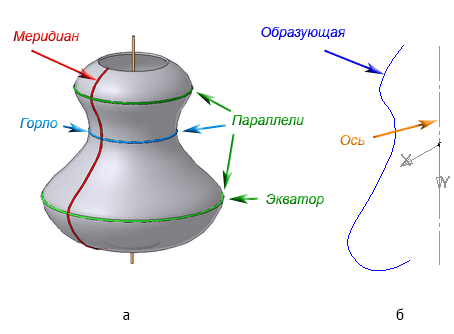
Рисунок 7.5 – Элементы поверхности вращения
Каждая точка образующей линии при вращении вокруг оси описывает окружность, которая располагается в плоскости, перпендикулярной оси вращения. Эти окружности называются параллелями (Рисунок 7.5).
Наименьшая параллель называется горлом , наибольшая – экватором .
Линия пересечения поверхности вращения плоскостью, проходящей через ось, называется меридианом .
Линия пересечения поверхности вращения плоскостью, проходящая через ось, параллельно фронтальной плоскости проекций, называется главным меридианом .
Видео:Метод эксцентрических сферСкачать

7.3. Цилиндрическая поверхность
Цилиндрическая поверхность образуется движением прямой линии, которая в любом своём положении параллельна данному направлению и пересекает криволинейную направляющую (Рисунок 7.6).
Цилиндр – геометрическое тело, ограниченное замкнутой цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими все образующие данной поверхности.
Взаимно параллельные плоские фигуры, ограниченные цилиндрической поверхностью, называются основаниями цилиндра .
Если нормальное сечение (плоскость сечения перпендикулярна образующим) имеет форму окружности, то цилиндрическая поверхность называется круговой .
Если образующие цилиндрической поверхности перпендикулярны к основаниям, то цилиндр называется прямым, в противном случае – наклонным .
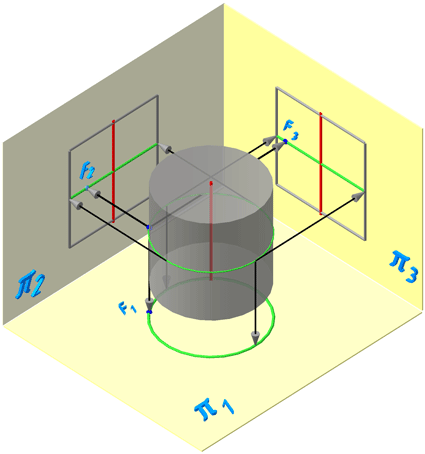
Рассмотрим проецирование прямого кругового цилиндра и принадлежащей ему точки F.
Условимся, что фронтальная проекция точки F – невидима (Рисунок 7.6).
Рисунок 7.6 – Проецирование цилиндра на плоскости проекций
Горизонтальная и профильная проекции точки F будут видимы.
При определении видимости, образующие, которые находятся на части, обращённой к наблюдателю и обозначенной на π1 сплошной зелёной линией – на плоскости проекции π2 видны, а которые находятся на части, обозначенной толстой штриховой линией – видны на π3.
Пусть точка А на π2 видима (Рисунок 7.7). Тогда на π1 она будет видима, а на π3 невидима.
Рисунок 7.7 – Эпюр прямого кругового цилиндра и принадлежащих ему точек
Видео:Геометрия 11 класс (Урок№8 - Сфера и шар.)Скачать

7.4. Пересечение прямой с поверхностью прямого кругового цилиндра
Для построения точек пересечения прямой линии с поверхностью прямого кругового цилиндра не требуется дополнительных построений. На горизонтальной плоскости проекций точки пересечения (1 и 2) находятся сразу. Фронтальные проекции строим по линиям связи.
Но в общем случае, алгоритм решения рассмотрим на следующем упражнении.
Рисунок 7.8 – Пересечение прямой с поверхностью прямого кругового цилиндра
Видео:Математика 5 класс (Урок№26 - Окружность и круг. Сфера и шар.)Скачать

Упражнение
Заданы: прямой круговой цилиндр с осью вращения, перпендикулярной плоскости проекций π1 и прямая а общего положения (Рисунок 7.8).
Построить точки пересечения прямой а с поверхностью цилиндра.
Для построения точек пересечения прямой с поверхностью цилиндра необходимо:
- Заключить прямую во вспомогательную секущую плоскость частного положения σ (горизонтально-проецирующую).
- Построить фигуру пересечения поверхности цилиндра горизонтально-проецирующей плоскостью: результат пересечения — четырехугольник (на π2 условно заштрихован).
- Найти точки «входа» и «выхода» прямой: на пересечении её фронтальной проекции с фронтальными проекциями сторон четырёхугольника (они же — проекции образующей цилиндра);
Прямая а пересекается со сторонами сечения в двух точках – 1 и 2.
Определим видимость участков прямой: очевидно, что между точками 1-2 прямая невидима, а на плоскости проекций π2 будет ещё невидим участок прямой от точки 1 до левой крайней образующей.
Видео:Поверхности вращенияСкачать

7.5. Пересечение прямой с поверхностью наклонного цилиндра
Видео:Лекция 5. Поверхности вращения. часть 1.Скачать

Упражнение
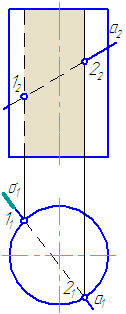
Заданы : наклонный круговой цилиндр с осью вращения, наклонной к плоскости проекций π1 и прямая mобщего положения (Рисунок 7.9).
Построить точки пересечения прямой mс поверхностью цилиндра.
Решение :
Для построения точек пересечения прямой с поверхностью цилиндра необходимо:
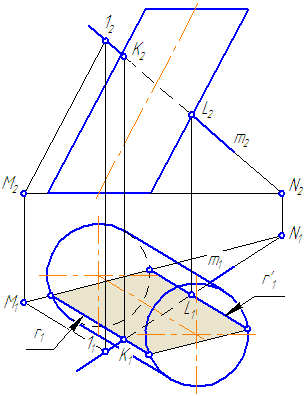
Рисунок 7.9 – Пересечение прямой с наклонным цилиндром
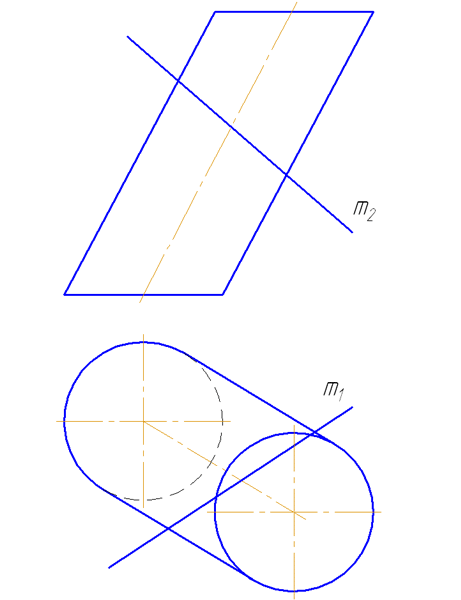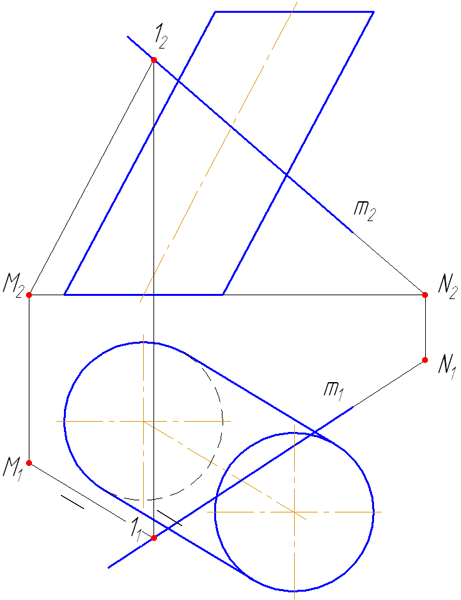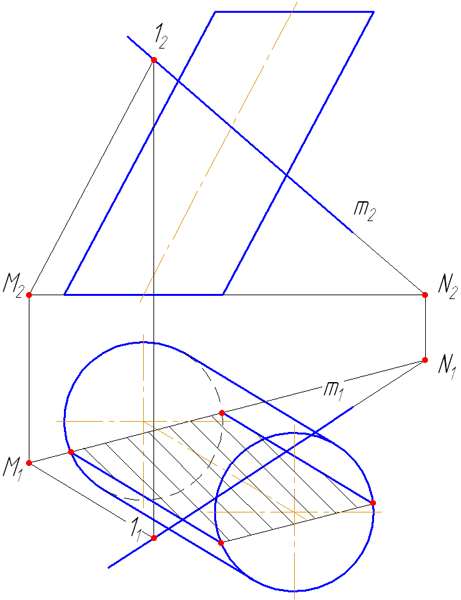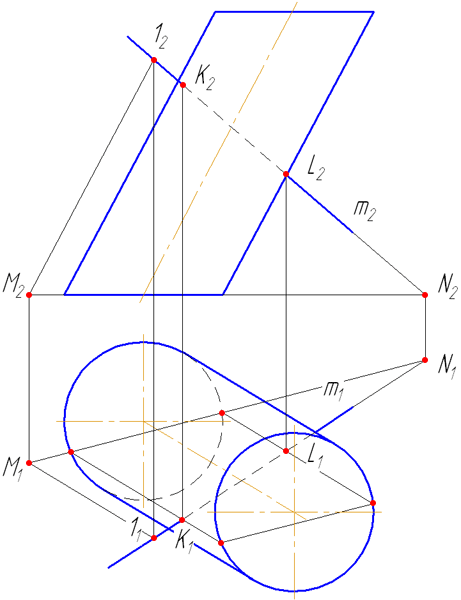
- Заключить прямую m во вспомогательную плоскость σ, дающую в сечении наиболее простую фигуру – четырехугольник (σ параллельна оси цилиндра или образующим). Эту плоскость зададим двумя пересекающимися прямыми m∩(1M);
- Построить горизонтальный след плоскости σ (прямую пересечения σ с плоскостью проекций π1) как проходящую через горизонтальные следы прямых m и (1M) (точки пересечения прямых с плоскостью проекций π1 (основания)) – (MN);
- Найти точки пересечения MN с окружностью основания цилиндра. Через эти точки провести образующие r, по которым плоскость σ пересекает боковую поверхность цилиндра:
На анимации ниже представлена последовательность построения точек пересечения прямой с наклонным цилиндром.
Видео:Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать

7.6. Сферическая поверхность
Сферическая поверхность – поверхность, образованная вращением окружности вокруг отрезка, являющегося её диаметром.
Шаром называется тело, ограниченное сферической поверхностью.
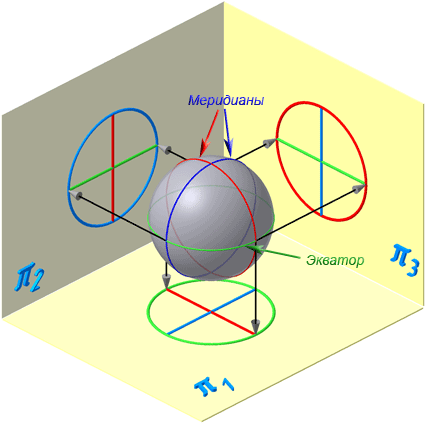
Экватор – это окружность, которая получается пересечением сферы горизонтальной плоскостью, проходящей через ее центр (Рисунок 7.10).
Меридиан – это окружность, которая получается пересечением сферы плоскостью, перпендикулярной плоскости экватора и проходящей через центр сферы.
Параллелями называются окружности, которые получаются пересечением сферы плоскостями, параллельными плоскости экватора.
Рисунок 7.10 – Проецирование сферической поверхности
Прямоугольная проекция шара (сферы) на любую плоскость – есть окружность, которую часто называют очерковой .
Рисунок 7.11 – Эпюр сферы и принадлежащих ей точек
Видео:Сфера и шарСкачать

Упражнение
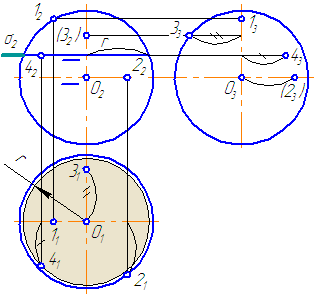
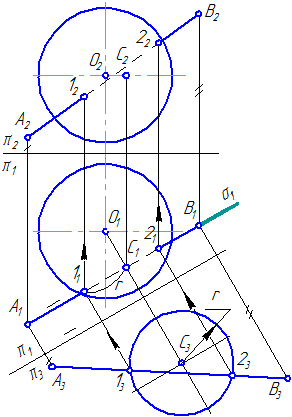
Заданы: сферическая поверхность тремя проекциями (Рисунок 7.11) и фронтальные проекции точек 1, 2, 3, 4.
Необходимо построить горизонтальные и профильные проекции заданных точек.
- Проанализируем их расположение на поверхности сферы. Точки 1, 2, 3 лежат на очерковых образующих сферы.
- Точка 1 принадлежит главному меридиану (очерковой окружности на π2), проекция которого на π1 совпадает с проекцией горизонтальной оси, на π3 – с проекцией вертикальной оси.
- Недостающие проекции точки 1 находим посредством линий проекционной связи. Все проекции точки 1 видимы.
- Рассмотрим положение точки 2. Точка 2 принадлежит экватору (очерковой окружности на π1), проекции которого на π2 и π3 совпадают с проекцией горизонтальной оси. Горизонтальная проекция точки 2 строится посредством линии проекционной связи, для построения профильной проекции необходимо измерить расстояние, отмеченное дугой, и отложить его по линии связи от точки О3 вправо. Профильная проекция точки 2 невидима.
- Точка 3 принадлежит очерковой окружности на π3, которая также является меридианом, проекции которого на π2 и π1 совпадают с проекцией вертикальной оси. Профильная проекция точки строится посредством линии проекционной связи. Для построения горизонтальной проекции точки 3 необходимо расстояние, отмеченное на π3 двумя засечками, отложить на π1 вверх от точки О1. Горизонтальная и профильная проекции точки 3 видимы.
- Для построения проекций точки 4 необходимо ввести вспомогательную секущую плоскость (зададим плоскость σ//π1 и σ⊥π2). Плоскость σ пересекает поверхность сферы по окружности радиусом r. На π1 строим данное сечение и по линии проекционной связи находим 41. Для построения профильной проекции необходимо расстояние, отмеченное засечкой, отложить по линии проекционной связи на π3 вправо от оси. Все проекции точки 4 видимы.
Видео:11 класс. Геометрия. Сфера и шар. Объем шара и площадь поверхности. 05.05.2020.Скачать

7.7. Пересечение прямой с поверхностью сферы
Видео:Лекция № 9 Поверхности. Классификация. Нелинейчатые поверхности вращения. Сфера.Скачать

Упражнение
Заданы: сфера и прямая общего положения АВ.
Найти: точки пересечения прямой с поверхностью сферы (точки «входа» и «выхода»).
Чтобы найти точки пересечения прямой с поверхностью сферы необходимо:
- Заключить прямую во вспомогательную плоскость, пересекающую поверхность сферы так, чтобы получались простые фигуры (например, круг, ограниченный окружностью);
- Построить фигуру пересечения сферы вспомогательной плоскостью;
- Найти общие точки прямой и контура фигуры (окружность): так как прямая и окружность лежат в одной плоскости, то они, пересекаясь, образуют точки, общие для прямой и сферы, которые и будут являться искомыми точками (Рисунок 7.12).
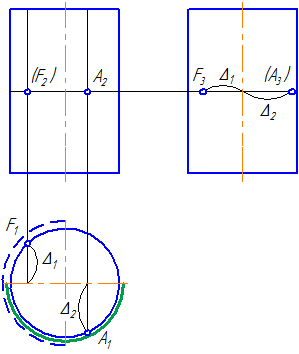
- Через прямую проводим плоскость σ. Пусть σ⊥π1 и пересекает сферу по окружности радиусом r. С – центр окружности сечения ОС⊥σ:
Рисунок 7.12 – Пересечение прямой с поверхностью сферы
- Введём π3⊥π1 и π3//σ1. Построим проекцию окружности сечения на π3 и проекцию А3В3.
- Находим точки их пересечения 12 и 23.
- Определим видимость участков прямой.
- На π1 точки 1 и 2 находятся на переднем полушарии, следовательно, на π2 они видимы.
Видео:Геометрия 11 класс (Урок№9 - Взаимное расположение сферы и тел вращения.)Скачать

7.8. Коническая поверхность
Коническая поверхность образуется движением прямой линии (образующей), которая в любом своем положении проходит через неподвижную точку и пересекает криволинейную направляющую (имеет две полости).
Тело, ограниченное замкнутой конической поверхностью вершиной и плоскостью, называется конусом .
Плоская фигура, ограниченная конической поверхностью, называется основанием конуса .
Часть конической поверхности, ограниченная вершиной и основанием, называется боковой поверхностью конуса .
Если основание конуса является кругом, то конус называется круговым .
Если вершина конуса расположена на перпендикуляре к основанию, восстановленному из его центра, то конус называется прямым круговым .
Рисунок 7.13 – Принадлежность точки конической поверхности
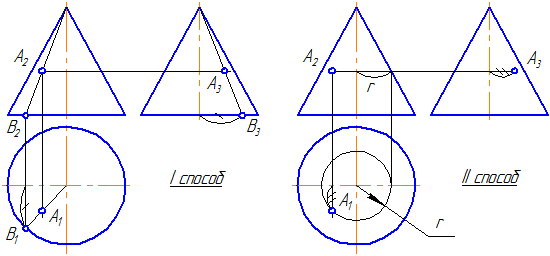
Рассмотрим вопрос принадлежности точки А поверхности конуса.
Дана фронтальная проекция точки А и она видима (Рисунок 7.13).
1 способ . Для построения ортогональных проекций точки, расположенной на поверхности конуса, построим проекции образующей, проходящей через данную точку. При таком положении точки А все её проекции – видимы.
2 способ . Точка А лежит на параллели конуса радиусом r. На π1 строим проекцию окружности (параллели) и по линии проекционной связи находим А1. По двум проекциям точки строим третью.
Видео:Геометрия 9 класс (Урок№34 - Тела и поверхности вращения.)Скачать

7.9. Пересечение прямой с поверхностью конуса
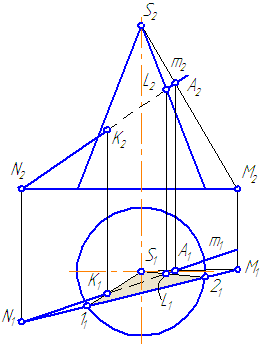
Пусть задан прямой круговой конус и прямая общего положения m (Рисунок 7.14). Найти точки «входа» и «выхода» прямой с поверхностью конуса.
- Через прямую m проводим вспомогательную секущую плоскость σ, дающую в сечении наиболее простую фигуру.
- Применение в качестве вспомогательной секущей плоскости проецирующей плоскости в данном случае нецелесообразно, так как в сечении получится кривая второго порядка, которую нужно строить по точкам.
Наиболее простая фигура – треугольник. Для этого секущая плоскость σ должна пройти через вершину S. Плоскость зададим с помощью двух пересекающихся прямых σ=SM∩MN или, что, то же самое, (σ=SM∩m).
- Возьмем на прямой m точку А и соединим её с вершиной. Прямая SA пересечёт плоскость основания в точке М.
- Построим горизонтальные проекции этих объектов.
- Продлим фронтальную проекцию прямой m до пересечения с плоскостью основания в точке N.
Рисунок 7.14 – Построение точек пересечения прямой с поверхностью конуса
- Построим её горизонтальную проекцию.
- Соединим точки M1N1, на пересечении с окружностью основания получим точки 1 и 2.
- Строим треугольник сечения конуса плоскостью σ, соединив точки 1 и 2 с вершиной S.
- На пересечении образующих 1-S и 2-S с прямой m получим искомые точки K и L.
- Определим видимость прямой относительно поверхности конуса.
На анимации ниже представлена последовательность построения точек пересечения прямой с поверхностью конуса.
Видео:Сфера и шар. Сечение сферы. Вписанная и описанная сфераСкачать

7.10. Пересечение цилиндра плоскостью
Пусть плоскость сечения γ – фронтально-проецирующая (Рисунок 7.15).
- Если плоскость сечения γ параллельна оси цилиндра, то она пересекает цилиндр по четырехугольнику.
- Если плоскость сечения γ перпендикулярна оси цилиндра, то она пересекает цилиндр по окружности.
- Если плоскость сечения γ не параллельна и не перпендикулярна оси цилиндра в сечении эллипс.
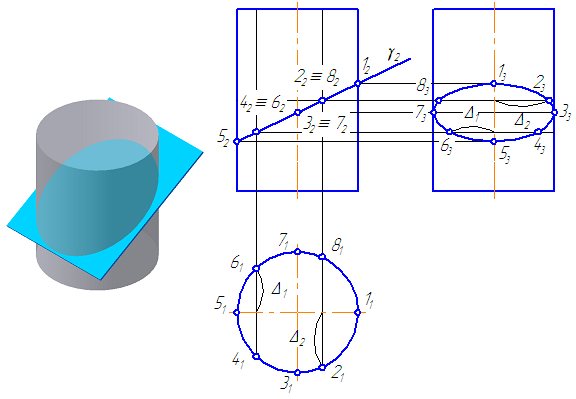
Рассмотрим алгоритм построения сечения – эллипс (Рисунок 7.15):
Рисунок 7.15 – пересечение цилиндра плоскостью
- Находим и строим характерные точки (точки, не требующие дополнительных построений) – в нашем случае, точки принадлежащие крайним образующим – 1, 3, 5, 7. Одновременно с этим, данные точки определяют величину большой и малой оси эллипса.
- Для построения участка эллипса необходимо построить не менее 5-ти точек (так как лекальная кривая второго порядка определяется как минимум пятью точками). Для построения точек 2, 4, 6, 8 возьмем на π1 произвольно расположенные образующие цилиндра, которые проецируются на данную плоскость проекции в точки.
- Построим вторые проекции данных образующих. Из точек пересечения вторых проекций образующих с проекцией плоскости сечения γ проводим линии связи к π3. Для построения третьей проекции, например, точки 6 измеряем расстояние Δ1 и откладываем его по соответствующей линии связи на π3. Симметрично ей, относительно оси вращения, строим точку 4. Аналогично строятся другие точки.
Видео:Построение недостающих проекции сквозного отверстия в сфереСкачать

7.11. Пересечение сферы плоскостью
Плоскость пересекает поверхность сферы всегда по окружности. Задачу пересечения плоскости со сферой мы рассматривали при решении задачи построения точек пересечения прямой с поверхностью сферы (см. выше).
Видео:Урок 19. Задачи на тела вращения из ЕГЭ. Цилиндр, конус, сфера. Стереометрия с нуля.Скачать

7.12. Пересечение конуса плоскостью
Рассмотрим пять возможных вариантов расположения плоскости относительно поверхности прямого кругового конуса. Пусть плоскость сечения перпендикулярна плоскости проекций π2 (Рисунок 7.16).
- Если плоскость проходит через вершину (1) – в сечении две образующие и прямая пересечения с плоскостью основания.
- Если плоскость перпендикулярна оси вращения конуса (2) – в сечении окружность.
- Если плоскость не параллельна ни одной образующей (пересекает все образующие (3)) – в сечении эллипс.
- Если плоскость параллельна одной образующей конуса – в сечении парабола (на примере – плоскость сечения (4) параллельна крайней образующей конуса).
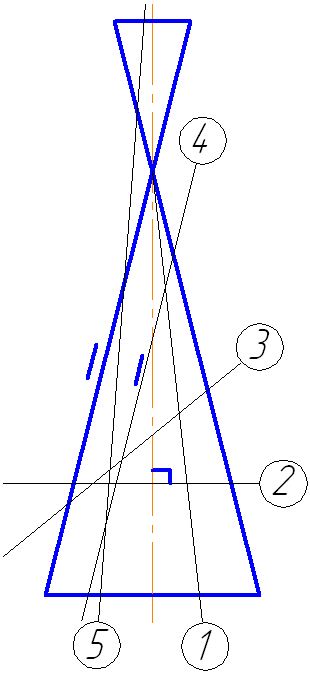
- Если плоскость параллельна двум образующим (пересекает обе полости конической поверхности (5)) – в сечении гипербола (рисунок 7.17).
Рисунок 7.17. Плоскость сечения параллельна двум образующим конуса
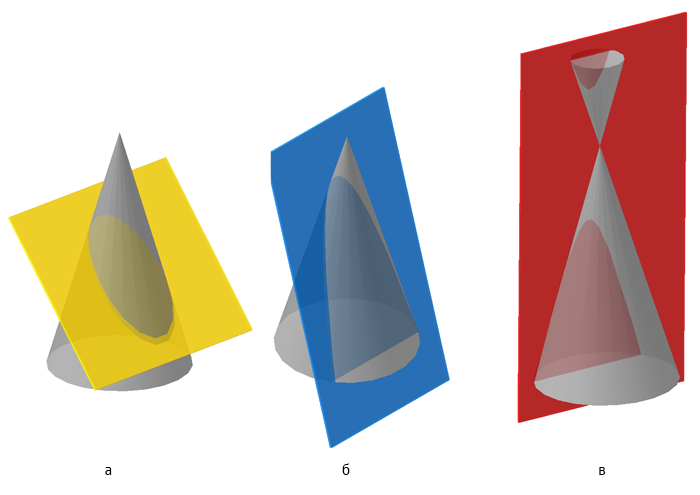
Ниже, на моделях, представлены варианты положения секущей плоскости относительно поверхности конуса, при которых получаются сечения в виде эллипса, параболы и гиперболы.
Рисунок 7.18 – Сечение конической поверхности плоскостью (а — эллипс, б — парабола, в — гипербола)
Рассмотрим пример построения сечения конической поверхности плоскостью.
Рисунок 7.19 – Построение пересечения конической поверхности плоскостью
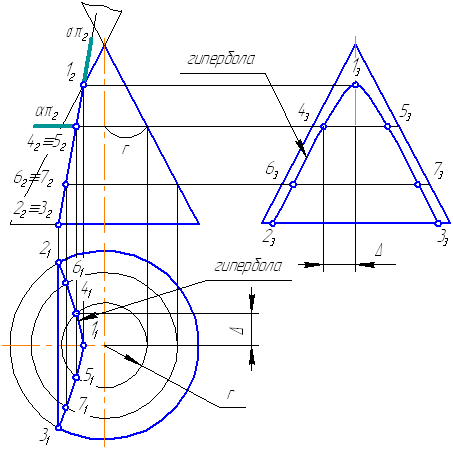
Пусть задана секущая проецирующая плоскость σ⊥π2 (Рисунок 7.19). Если продлить коническую поверхность и проекцию плоскости, то видно, что плоскость пересекает вторую ветвь конической поверхности, следовательно, в сечении получится гипербола.
- Построим характерные точки. Это точки, лежащие на крайних образующих и на окружности основания конуса (1, 2, 3). Их проекции строятся по линиям проекционной связи.
- Для построения промежуточных точек, воспользуемся методом вспомогательных секущих плоскостей. Введём плоскость α⊥π2 и перпендикулярно оси вращения, что даст в сечении окружность радиусом r. Строим эту окружность на π1. Плоскость α пересекает и заданную плоскость сечения по прямой, проекции которой на π1 и π3 совпадают с линиями проекционной связи.
- На пересечении этих двух сечений на плоскости проекций π1 строим точки 4, 5. Профильные проекции этих точек строим по линии проекционной связи, откладывая расстояние от оси вращения конуса, равное Δ.
- Аналогично строим точки 6, 7. Плавно соединим построенные точки, образуя гиперболу.
- Обведём то, что осталось от конуса после такого среза с определением видимости. В нашем примере все проекции построенной кривой будут видимы.
На анимации ниже представлена последовательность построения пересечения конической поверхности плоскостью.
Видео:13. Вращение сферыСкачать

7.13. Задачи для самостоятельной работы
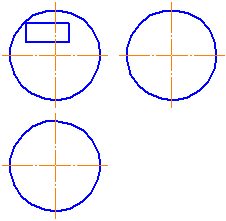
1. Достроить проекции сферы с заданным вырезом (Рисунок 7.20).
Рисунок 7.20
2-3. Построить три проекции конуса с призматическим отверстием (Рисунки 7.21, 7.22).
Рисунок 7.21
Рисунок 7.22
4. Построить точки «входа» и «выхода» прямой при пересечении её с поверхностью полусферы (Рисунок 7.23).
Рисунок 7.23
Урок геометрии на тему «Сфера и шар. Уравнение сферы». 11-й класс
Разделы: Математика
Класс: 11
Цель: Определение шара и сферы (шаровой поверхности) и связанных с ним понятий (центр, радиусы, диаметры, диаметрально противоположные точки). Рассмотреть уравнение сферы.
Оборудование: плакаты, модели шара, сферы.
2) Проверка домашнего задания.
3) Повторить определение окружности, уравнение окружности. Решить устно две задачи.
2. Изучение нового материала.
1) Определение сферы и шара (на моделях и рисунках) №574 (а).
2) Уравнение сферы.
3) Решение устных примеров.
3. Закрепление материала. № 576 (а), 576 (б)-С, 578 (г), 577 (а), 579 (а, б)
4. Домашнее задание: параграф 3. П 58,59. №576 (б), 577 (б), 579(в, г), 574(б).
6. Решение задач повышенной сложности.
1) Организационный момент
2) Проверка домашнего задания.
3) Учитель: Ребята, вам на дом было повторить определение окружности, круга, расстояние между двумя точками в пространстве. Уравнение окружности.
Показываю плакат окружности, круга и повторяем определение.
Ученики:
Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки.
Круг – часть плоскости, ограниченная окружностью.
Учитель: Напишите, пожалуйста, на доске уравнение окружности (x-x0) 2 + (y-y0) 2 = R 2 , где (x0; y0)- центр окружности, R- радиус, (x; y)- координата центра окружности.
Устно. Найти уравнение окружности?
1) (x-4) 2 +(y-3) 2 =9. 2) x 2 + y 2 =4. 3) (0-4) 2 +(0-3) 2 =R 2 . 4) 16+9=R 2 .
5)25=R 2 . 6) R=5. 7)(x+4) 2 +(y-3) 2 =25.
Учитель: Найдите расстояние М1 М2, если М1 (-3; 0; 4), М2 (0; 6; 5). М1 М2 = (0-3) 2 + (6-0) 2 +(5-4) 2 = 46.
Следовательно, d= (x-x) 2 +(y-y) 2 + (z-z) 2 .
2. Объяснение нового материала. Сфера.
1) Учитель: Геометрия изучает форму и взаимное расположение фигур в пространстве. Мы живем в мире трех измерений.
Окружность и круг это пространственные тела или плоские?
В какое геометрическое тело превратится окружность (круг), если попадет в пространство?
Ученики: В сферу и шар.
Учитель: (показывает плакаты) Остановимся на сфере.
1). Сферу можно получить вращением полуокружности вокруг ее диаметра как оси.
2). Границы шара называется шаровой поверхностью или сферой.
3). Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.
Обозначение. (Рассказываю с помощью плаката) : Радиус, диаметр, центр сферы D=2R, обозначение сферы 
1. Шар — может быть получен вращением полукруга вокруг диаметра как оси.
2. Шаром называется тело, ограниченное сферой.
3. Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки.
Эта точка называется Центром шара. А данное расстояние – радиусом шара. Отрезок соединяющий две точки шаровой поверхности проходящей через ее центр – называется диаметром.
А теперь запишем число, тему: п. 48. Шар. Сфера.
В тетрадях рисуем один чертеж, пишем определения и обозначения. Пишем три определения шара и сферы. (под диктовку)
3. Закрепление. №574 (а, б)
Дано: сфера, т О — центр, R — радиус т.А и В € 
Найти: ОМ.
Решение. а) ОА=ОВ= R=50 см. Следовательно треугольник АОВ — равнобедренный —> ОМ — высота (по свойству медианы в равнобедренном треугольнике). Рассмотрим треугольник АОМ (LО=90 0 ). По теореме Пифагора
ОМ= v АО 2 – АМ 2 = v 2500-400 = v 2100 =10 v21 (см).
Самостоятельно б) ОМ= v 225-81 = v 144= 12 (мм) Ответ: 10 v21 см; 12 мм.
Уравнение сферы. П 59.
Пусть задана прямоугольная система координат Охуz и дана некоторая поверхность. Уравнение с тремя переменными х, у, z, называется уравнением поверхности, если этому уравнению удовлетворяют координаты любой точки F и не удовлетворяют координаты никакой точки не лежащей на этой поверхности.
Дано: прямоугольная система координат Охуz сфера 
Написать уравнение сферы.
Решение: Возьмем произвольную т М (x;y;z). Расстояние от М до С, МС= v (x-x0) 2 +(y-y0) 2 + (z-z0) 2 если точка М € 
Если М € 
5. Закрепление по теме: уравнение сферы №576(а, б), 578, 577 (а).
№576. Напишите уравнение сферы радиуса R с центром в центре А, если а) А(2;-4; 7), R=3.
Ответ (x-2) 2 +(y+4) 2 + (z-7) 2 =9 2 .
Б) А(0;0;0) R= v 2. Ответ: x 2 +y 2 + z 2 =2.
№578 а) А(0;0;0) , R=7. Б) А(3; -2; 0), R= v 2.
№577 а) Дано: сфера 
Найти: уравнение сферы.
(5-2) 2 +(0-2) 2 + (-1-0) 2 = R 2 .
(x+2) 2 +(y-2) 2 + z 2 =54.
Учитель: Ребята, как записывается уравнение сферы, если ее центр лежит в т (х0, 0, 0), а радиус равен R.
(x-x0) 2 +y 2 + z 2 =R 2 .
x 2 — 2xx0+x0 2 +y 2 +z 2 = R 2 .
x 2 — 2xx0 +y 2 +z 2 = R 2 -x0 2 — уравнение сферы.