Как построить правильный четырехугольник в окружности

С помощью циркуля и линейки опишите около окружности правильный четырёхугольник.

То есть у нас есть окружность, а вокруг неё надо описать квадрат. Но как? с помощью циркуля и линейки

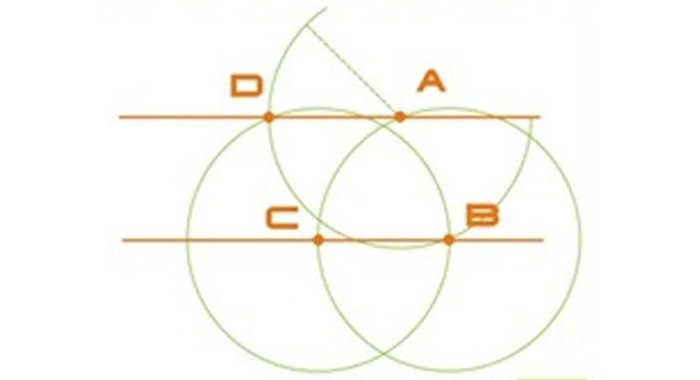
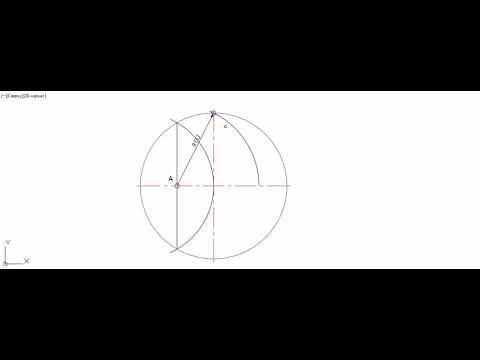
Через центро окружности проводим прямую. На точках пересечения этой прямой и окружности отмечаем точки (назову их А и В) . Проводим 2 окружности, радиусы которых равны и (чуть) больше радиуса этой окружности. Через точки пересечения радиусов проводим прямую (построили перпендикуляр через центр точно) . Там, где этот перпендикуляр пересекает окружность, данную изначально, отмечаем точки (назову их С и D). Соединяем точки (А, С, В, D) и получится четырехугольник (ACBD или ADBC, как точки поставите. ) .
.

Радиус окружности будет равен половине стороны квадрата. Центр — это точка пересечения диагоналей квадрата

Чтобы стороны четырехугольника соприкасались с окружностью. С помощью циркуля рисуешь окружность, а с помощью линейки квадрат. Вроде всё понятно написано.

Я бы так сделала.
Проводим диаметр. Наша задача построить перпендикуляры к диаметру из его крайних точек. Делаем это при помощи циркуля ( сначала насечки справа-слева) , потом из насечек еще по- бол диаметром насечки, соединяем . Длина =R Всего D

Видео:Построение пятиугольника циркулемСкачать

Постройте: а) правильный четырехугольник, вписанный в окружность; б) правильный треугольник, описанный около окружности; в) правильный четырехугольник,

Видео:ПОСТРОИТЬ ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК [construction a regular pentagon]Скачать

Ваш ответ

Видео:Построение пятиугольника циркулем и линейкойСкачать

решение вопроса

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,658
• разное 16,822

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Построение пятиугольникаСкачать

Построение с помощью циркуля и линейки — описание, алгоритмы и задачи

Построение с помощью циркуля и линейки – древнейший способ расчета в евклидовой геометрии. Известен со времен Древней Греции. Данная тема изучается в средних и старших классах на уроках геометрии.

Рассмотрим все случаи построения на конкретных примерах.

Видео:Как построить квадрат, два способаСкачать

Построение отрезка, равного данному

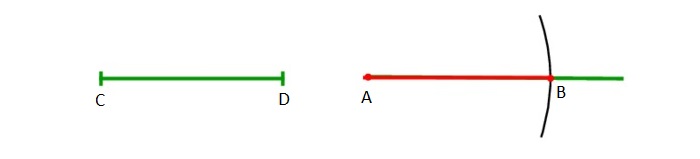
Есть отрезок СD. Задача — начертить равнозначный данному отрезок той же величины.

Строится луч, имеющий начало в т. A. Циркуль отмеряет существующий отрезок CD. Циркулем откладывается отрезок, равнозначный первому отрезку, на том же начерченном луче от его начала (A).

Для подобного чертежа ножку с иглой закрепляют в начале луча A, а с помощью части с грифелем проводится дуга до места соприкосновения с лучом. Данную точку можно обозначить т. B.

Отрезок AB будет равнозначен отрезку СD. Задача решена.

Видео:Как построить правильный шестиугольник.Скачать

Деление отрезка пополам

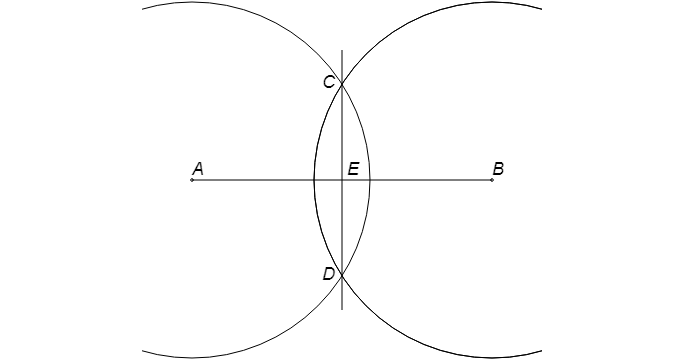
Имеется отрезок AB.

Сначала следует нарисовать окружность с радиусом больше половины отрезка AB с центром в т. A.

Далее чертится круг с тем же радиусом с серединой в т. B. В местах пересечения окружностей имеем т. C и т. D.

Сквозь эти точки требуется провести прямую линию. Получаем т. E, которая будет серединой отрезка AB.

Видео:Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Построение угла, равного данному

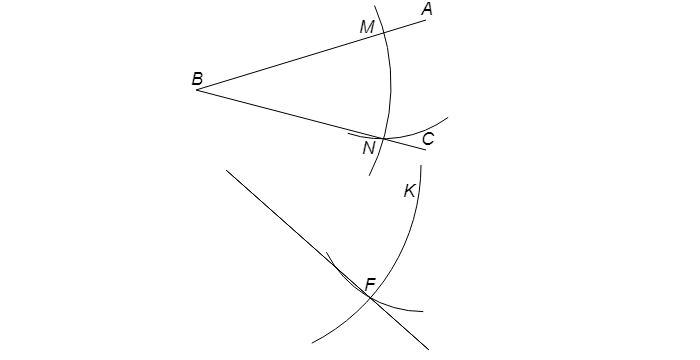
Имеется угол ABC.

Вблизи угла проводится луч ED. Далее чертится окружность с серединой в т. B. В итоге имеем точки M и N.

Оставив раствор циркуля прежним, рисуют круг с серединой в т. E. В точке соприкосновения имеем т. K.

Поменяв раствор циркуля на длину расстояния между т. M и т. N, нужно провести окружность с серединой в т. K. В итоге получается т. F. После чертится прямая из т. E через т. F. Образуется угол DEF, который будет равнозначен углу ABC. Задача решена.

Видео:Геометрия - Построение шестиугольникаСкачать

Построение перпендикулярных прямых

Пример 1

Точка O находится на прямой a.

Есть прямая и точка, находящаяся на ней. Нанести линию, идущую через существующую точку и находящуюся под прямым углом к имеющейся прямой.

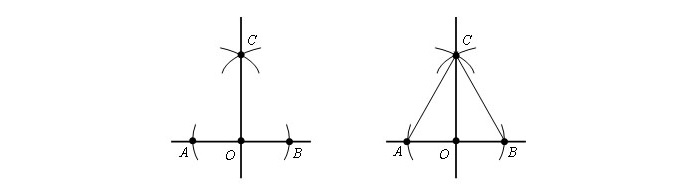
Шаг 1. Чертим круг с рандомным радиусом r с серединой в т. O. Окружность соприкасается с прямой в т. A и т. B.

Шаг 2. Из имеющихся точек строится круг с радиусом AB. Точки С и D являются точками соприкосновения окружностей.

Приложив линейку, чертят прямую, сквозь т. O и одну из т. C или т. D, к примеру отрезок OC.

Доказательство, что прямая OC лежит перпендикулярно a.

Намечаются два отрезка — AC и CB. Получившиеся треугольники будут равны, согласно третьему признаку равенства треугольников. Значит, прямая CO перпендикулярна AB.

Пример 2

Точка O находится вне прямой а.

Нарисовать окружность с радиусом r из т. O. Она должна проходить сквозь прямую a. A и B — точки её соприкосновения с прямой.

Оставив прежний радиус, рисуем окружности с серединой в т. A и т. B. Точка O₁ — место их соприкосновения.

Рисуем линию, соединяющая т. O и т. O1.

Доказательство выглядит следующим образом.

Две прямые ОО₁ и AB пересекаются в т. C. Согласно третьему признаку равенства всех треугольников AOB = BO₁A. Из данного вывода следует, что угол OAC = O₁AC. Одноименные треугольники также будут равны (согласно первому признаку равенства всех треугольников).

Исходя из этого, выводим, что угол OCA = O₁CA, а, учитывая смежность углов, приходим к пониманию, что они прямые. А это означает, что OC – перпендикулярный отрезок, опущенный из т. O на прямую a. Задача решена.

Видео:Как нарисовать правильный пятиугольник | Видеоурок MATHANIMATIONСкачать

Построение параллельных (непересекающихся) прямых

Имеется прямая и т. А, не лежащая на этой прямой.

Нужно отметить прямую, проходящую через т. A, и параллельную имеющейся прямой.

Берется рандомная точка на имеющейся прямой и именуется B. С помощью циркуля строится окружность радиуса AB с серединой в т. B. В месте пересечения окружности и данной прямой отмечается т. C.

Оставив прежний радиус, рисуется еще одна окружность, теперь уже с центром в т. C. При правильных расчетах дуга должна пройти через т. B.

C тем же радиусом AB строится окружность с серединой в т. A. Точку соприкосновения второй и третьей окружностей назовем D. Третья окружность, учитывая верность расчетов, также пройдет через т. B.

Проводится прямая через т. A и т. D, которая станет параллельной первой. В итоге, получились две параллельные прямые, BC и AD.

Видео:Построение 8 угольника циркулемСкачать

Построение правильного треугольника, вписанного в окружность

Правила построения правильного треугольника, вписанного в окружность:

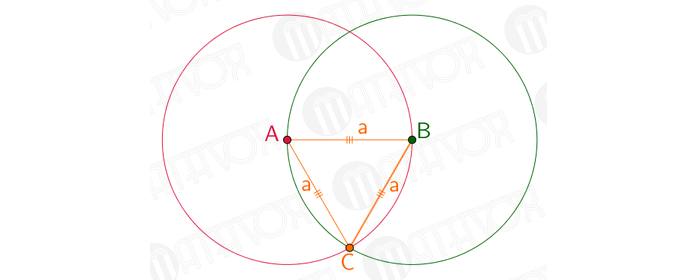
Отметить отрезок AB, чья длина будет равняться а.

Взять циркуль. Часть с иголкой расположить на т. А, а часть с карандашом на т. B. Прочертить окружность. В итоге, радиус круга будет равнозначен длине отрезка AB.

Далее иглу размещают на т. B, а часть с грифелем на т. A. Чертится круг. В итоге, его радиус будет равнозначен длине отрезка AB.

На чертеже окружности пересеклись в двух точках. Далее нужно соединить т. A и т. B и одну из вышеупомянутых точек. В результате получится равносторонний треугольник.

Стороны такого треугольника равнозначны радиусам двух окружностей, которые равны длине а. Задача решена.

Видео:4K Как построить правильный пятиугольник, how to draw a regular pentagonСкачать

Построение правильного четырехугольника вписанного в окружность

Вариант 1

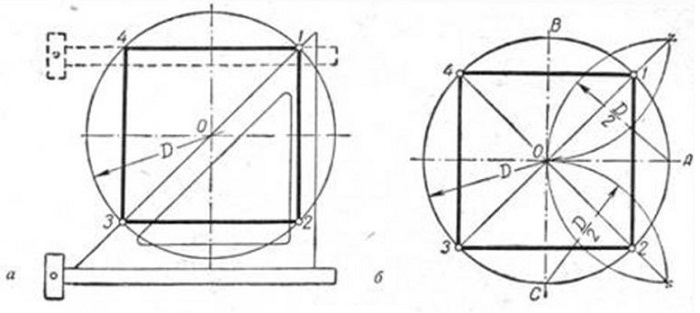
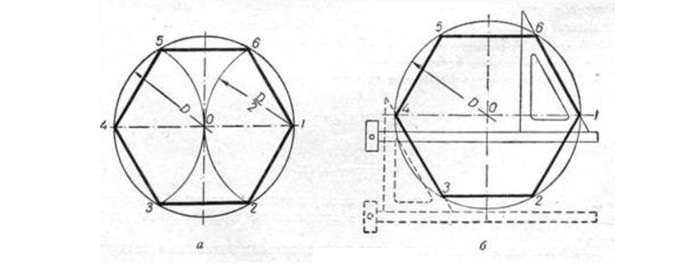
Исходя из данности, что диагонали любого квадрата пересекаются в середине окружности и находятся по отношению к его осям под углом 45 градусов, производят следующие действия. Пользуясь линейкой и уголком с углами 45 градусов (см. рисунок), размечают вершины т. 1 и т. 3.

Сквозь данные точки чертят отрезки, стороны четырехугольника, расположенные по горизонтали. Это т. 4 и т. 1, т. 3 и т. 2. В конце линейкой и уголком по его катету проводятся линии, расположенные по вертикали (высоты), отрезок т.1 — т. 2 и отрезок т. 4 — т. 3.

Вариант 2

Так как вершины правильного четырехугольника разделяют наполовину дуги окружностей, между точками диаметра (см. рисунок), то для достижения результата делают следующее: отмечают на точках перпендикулярных диаметров т. A, т. B и т. C и рисуют дуги до их соприкосновения.

После чертят прямые через места соприкосновения дуг, которые выделены на фигуре линиями. Точки соприкосновения с окружностью будут являться вершинами — это т. 1 и т. 3, т. 4 и т. 2. Данные вершины полученного квадрата соединяют друг с другом.

Задача выполнена двумя способами.

Видео:Как построить шестиугольник вписанный в окружностьСкачать

Построение вписанного в окружность правильного пятиугольника

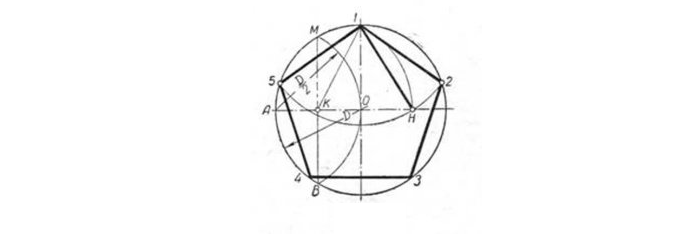
Поместить на окружность т. 1, считая ее за вершину пятиугольника. Разделить отрезок AO пополам. Чтобы произвести подобную операцию, из т. A чертят дугу до места соприкосновения с окружностью в т. M и т. B.

Расположив конкретные точки на прямой, получаем т. K, и после совмещаем с т. 1. Радиусом, длина которого – отрезок А1, сделать изгиб из т. K до места соприкосновения с линией АО в т. H. После совместить т. 1 и т. H, образуя одну из пяти сторон пятиугольника.

Взять циркуль, величина раствора которого будет равна отрезку т.1 — т. H, нарисовать изгиб из т. 1 до соприкосновения с кругом. Так находят вершины 2 и 5. Отметив точки на вершинах 2 и 5, получают вершины 3 и 4. В конце все точки совмещают друг с другом.

Видео:Как вписать квадрат в окружностьСкачать

Построение правильного шестиугольника, вписанного в окружность

Решение подобной задачи строится на свойствах, где сторона шестиугольника равнозначна радиусу круга.

Для расчета разделяют круг на шесть ровных частей и последовательно совмещают все полученные точки (см. рисунок). Задача решена.

💡 Видео

Как начертить пятиугольник вписанный в круг или звездаСкачать

Деление окружности на 5 частей с помощью циркуляСкачать

Построение правильного восьмиугольника.Скачать

Построение шестнадцатиугольника циркулемСкачать

Построение правильного квадрата.Скачать

Построение 12 угольника циркулемСкачать