Геометрия | 5 — 9 классы
Диагональ АС невыпуклого четырехугольника ABCD разделяет этот четырехугольник на два треугольника, причем АС> ; ВС, АВ = AD, DC = CD, а прямые, содержащие диагонали четырехугольника, пересекаются в точке О Сравните периметры пятиугольников BCODA и DCOBA.
В условии задачи опечатка.
Диагональ АС невыпуклого четырехугольника ABCD разделяет этот
четырехугольник на два треугольника, причем АС> ; ВС,
АВ = AD, ВС = CD, а
прямые, содержащие диагонали
четырехугольника, пересекаются в точке О Сравните периметры пятиугольников BCODA и DCOBA
Условие АС> ; ВС нужно только для того, что бы правильно построить четырехугольник.
- Диагонали четырехугольника ABCD пересекаются в точке M, причем AM = MC = BM = MD?
- Диагонали четырехугольника ABCD пересекаются в точке о известно что треугольники AOB = COD?
- В четырехугольнике ABCD BC || AD и BC = AD, AC = 30 см,BD = 12 см, AB = 10 см?
- В четырехугольнике АВСD диагональ АС делит ∠А пополам?
- Диагонали четырехугольника ABCD пересекаются в точке О и точкой О делятся пополам ?
- Пусть прямая, параллельная диагонали AC выпуклого четырехугольника ABCD и проходящая через середину его диагонали BD, пересекает сторону AD в точке E?
- В четырехугольнике ABCD , BC||AD и AB||CD?
- Диагональ АС невыпуклого четырехугольника АВСD, в котором АВ = АD> ; ВС = СD, разделяет его на 2 треугольника?
- Найдите сторону AD четырехугольника ABCD , если АВ = 3 ; ВС = 4 ; CD = 5 и известно , что в четырехугольник ABCD можно вписать окружность?
- В четырехугольнике abcd ab = bc = cd и ac = bd = ad?
- § 2. Параллелограмм и трапеция
- Параллелограмм
- Признаки параллелограмма
- Трапеция
- Задачи
- Ответы к задачам
- Урок «Четырёхугольники. Решение задач»
- «Календарь счастливой жизни: инструменты и механизм работы для достижения своих целей»
- «Управление общеобразовательной организацией: новые тенденции и современные технологии»
- Описание презентации по отдельным слайдам:
- 📺 Видео
Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Диагонали четырехугольника ABCD пересекаются в точке M, причем AM = MC = BM = MD?
Диагонали четырехугольника ABCD пересекаются в точке M, причем AM = MC = BM = MD.
Определите тип четырехугольника.
Видео:№479. Точки D и Е лежат на сторонах АВ и АС треугольника ABC. Найдите:Скачать

Диагонали четырехугольника ABCD пересекаются в точке о известно что треугольники AOB = COD?
Диагонали четырехугольника ABCD пересекаются в точке о известно что треугольники AOB = COD.
Докажите что данный четырехугольник параллелограмм.
Видео:№369. Найдите углы A, B и C выпуклого четырехугольника ABCD, еслиСкачать

В четырехугольнике ABCD BC || AD и BC = AD, AC = 30 см,BD = 12 см, AB = 10 см?
В четырехугольнике ABCD BC || AD и BC = AD, AC = 30 см,
BD = 12 см, AB = 10 см.
Диагонали четырехугольника пересекаются в
Найдите периметр треугольника COD.
Видео:В параллелограмме ABCD диагональ AC в 2 раза ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать

В четырехугольнике АВСD диагональ АС делит ∠А пополам?
В четырехугольнике АВСD диагональ АС делит ∠А пополам.
Известно, что АВ = 3, ВС = √3, CD = 2, AD = 4.
Найдите диагонали и углы четырехугольника АВСD /.
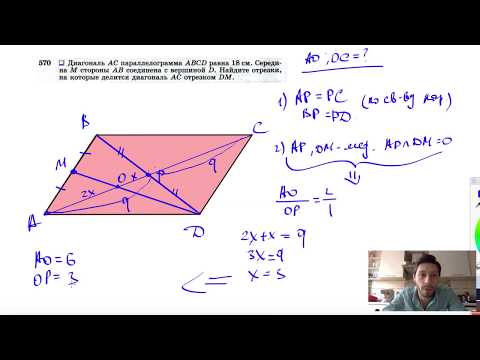
Видео:№570. Диагональ АС параллелограмма ABCD равна 18 см. Середина М стороны АВ соединенаСкачать
Диагонали четырехугольника ABCD пересекаются в точке О и точкой О делятся пополам ?
Диагонали четырехугольника ABCD пересекаются в точке О и точкой О делятся пополам .
Равны ли векторы :
AO и CO, AB и CD, BO и OD, BC и AD?
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Пусть прямая, параллельная диагонали AC выпуклого четырехугольника ABCD и проходящая через середину его диагонали BD, пересекает сторону AD в точке E?
Пусть прямая, параллельная диагонали AC выпуклого четырехугольника ABCD и проходящая через середину его диагонали BD, пересекает сторону AD в точке E.
Докажите, что прямая EC делит площадь четырехугольника ABCD пополам.
Видео:8 класс, 2 урок, Выпуклый многоугольникСкачать

В четырехугольнике ABCD , BC||AD и AB||CD?
В четырехугольнике ABCD , BC||AD и AB||CD.
Диагонали четырехугольника пересекаются в точке O .
Пириметер треугольника AOB равен 47 см, AC = 40 см, BD = 24 см.
Видео:№382. Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырехугольникСкачать

Диагональ АС невыпуклого четырехугольника АВСD, в котором АВ = АD> ; ВС = СD, разделяет его на 2 треугольника?
Диагональ АС невыпуклого четырехугольника АВСD, в котором АВ = АD> ; ВС = СD, разделяет его на 2 треугольника.
Прямые АС и ВD пересекаются в точке О.
Сравните периметры пятиугольников ВСОDА и DСОВА.
Если можно с чертежем.
Видео:2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать

Найдите сторону AD четырехугольника ABCD , если АВ = 3 ; ВС = 4 ; CD = 5 и известно , что в четырехугольник ABCD можно вписать окружность?
Найдите сторону AD четырехугольника ABCD , если АВ = 3 ; ВС = 4 ; CD = 5 и известно , что в четырехугольник ABCD можно вписать окружность.
Видео:3 правила для вписанного четырехугольника #shortsСкачать

В четырехугольнике abcd ab = bc = cd и ac = bd = ad?
В четырехугольнике abcd ab = bc = cd и ac = bd = ad.
Найдите все углы четырехугольника abcd.
Вы находитесь на странице вопроса Диагональ АС невыпуклого четырехугольника ABCD разделяет этот четырехугольник на два треугольника, причем АС> ; ВС, АВ = AD, DC = CD, а прямые, содержащие диагонали четырехугольника, пересекаются в ? из категории Геометрия. Уровень сложности вопроса рассчитан на учащихся 5 — 9 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.
Периметр исходного треугольника равен сумме периметров треугольников образованных медианой за вычетом удвоенной длины этой медианы. (13 + 16) — 6 * 2 = 29 — 12 = 17 см.
Решение задачи во вложенном файле.
A) Точка K  (начальная / точка луча KV. B) Начальная точка луча VK точка ( / v / c) прямые KV и VK  / совпадают) d) лучи KV и VK  / отличаеются) e) отрезки KV иVK (совпадают).
Իսծֆկ են ևէ`ձ 359 նշ լաց ել զի լսի no coment.
Что? у тебя нету ничего.
Ну так — с. 1) Центр вписанной окружности – точка пересечения биссектрис треугольника, то есть АО и ОС – это биссектрисы 2) Блин, я в тупике, прости Надеюсь, первый пункт тебе поможет❤️((((.
A(1 ; 1 ; 5) ; b(2 ; — 4 ; 6) ; c( — 5 ; 3 ; 1) 1) Скалярное произведение векторов. 2a — 2c = (2 ; 2 ; 10) — ( — 10 ; 6 ; 2) = (2 + 10 ; 2 — 6 ; 10 — 2) = (12 ; — 4 ; 8) b + 3a = (2 ; — 4 ; 6) + (3 ; 3 ; 15) = (2 + 3 ; — 4 + 3 ; 6 + 15) = (5 ; — 1 ;..
Сумма всех углов треугольника 180, значит один внешний будет 260 — 180 = 80. Тогда смежный с ним внутренний угол равен 180 — 80 = 100 Значит, что этот внутренний угол — это угол вершины равнобедренного треугольника, так как он не может быть углом пр..
Дано : NB — биссектриса∠MBC ; ∠ABC = 180° ; ∠NBC > ∠ABM на 15°. Найти : ∠NBC. Решение : пусть ∠NBC = x, значит и ∠МВN = x, т. К. NB является биссектрисой∠MBC. Выходит уравнение : 2x + х + 15° = 180°. 3x = 180° — 15°. Х = 165°÷3. Х = 55° — ∠NBC..
Видео:№552. Диагонали трапеции ABCD с основаниями АВ и CD пересекаются в точке О. Найдите:Скачать

§ 2. Параллелограмм и трапеция
Параллелограмм
| Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны. |
На рисунке 157 изображён параллелограмм ABCD: АВ || CD, AD || ВС. Параллелограмм является выпуклым четырёхугольником (см. задачу 378).
Рассмотрим некоторые свойства параллелограмма.
| 1 0 . В параллелограмме противоположные стороны равны и противоположные углы равны. |
Рассмотрим параллелограмм ABCD (рис. 158). Диагональ АС разделяет его на два треугольника: АВС и ADC. Эти треугольники равны по стороне и двум прилежащим углам (АС — общая сторона, ∠1 = ∠2 и ∠3 = ∠4 как накрест лежащие углы при пересечении секущей АС параллельных прямых АВ и CD, AD и ВС соответственно). Поэтому
AB = CD, AD = ВС и ∠B = ∠D.
Далее, пользуясь равенствами углов 1 и 2, 3 и 4, получаем
∠A = ∠1 + ∠3 = ∠2 + ∠4 = ∠C.
| 2 0 . Диагонали параллелограмма точкой пересечения делятся пополам. |
Пусть О — точка пересечения диагоналей АС и BD параллелограмма ABCD (рис. 159). Треугольники АОВ и COD равны по стороне и двум прилежащим углам (АВ = CD как противоположные стороны параллелограмма, ∠1 = ∠2 и ∠3 = ∠4 как накрест лежащие углы при пересечении параллельных прямых АВ и CD секущими АС и BD соответственно). Поэтому АО = ОС и OB = OD, что и требовалось доказать.
Рисунок 160 иллюстрирует все рассмотренные свойства.
Признаки параллелограмма
| 1 0 . Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник — параллелограмм.. |
Пусть в четырёхугольнике ABCD стороны АВ и CD параллельны и AB = CD (см. рис. 158).
Проведём диагональ АС, разделяющую данный четырёхугольник на два треугольника: АВС и CD А. Эти треугольники равны по двум сторонам и углу между ними (АС — общая сторона, АВ = CD по условию, ∠1 = ∠2 как накрест лежащие углы при пересечении параллельных прямых АВ и CD секущей АС), поэтому ∠3 = ∠4. Но углы 3 и 4 накрест лежащие при пересечении прямых AD и ВС секущей АС, следовательно, AD || ВС.
Таким образом, в четырёхугольнике ABCD противоположные стороны попарно параллельны, а значит, четырёхугольник ABCD — параллелограмм.
| 2 0 . Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник — параллелограмм. |
Проведём диагональ АС данного четырёхугольника ABCD, разделяющую его на треугольники АВС и CD А (см. рис. 158). Эти треугольники равны по трём сторонам (АС — общая сторона, AB = CD и BC = DA по условию), поэтому ∠1 = ∠2. Отсюда следует, что АВ || CD. Так как AB = CD и АВ || CD, то по признаку 1 0 четырёхугольник ABCD — параллелограмм.
| 3 0 . Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник — параллелограмм. |
Рассмотрим четырёхугольник ABCD, в котором диагонали АС и BD пересекаются в точке О и делятся этой точкой пополам (см. рис. 159). Треугольники АОВ и COD равны по первому признаку равенства треугольников (АО = ОС, BO = OD по условию, ∠AOB = ∠COD как вертикальные углы), поэтому AB = CD и ∠1 = ∠2. Из равенства углов 1 и 2 следует1, что АВ || CD.
Итак, в четырёхугольнике ABCD стороны АВ и CD равны и параллельны, значит, по признаку 1 0 четырёхугольник ABCD — параллелограмм.
Трапеция
Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны трапеции называются её основаниями, а две другие стороны — боковыми сторонами (рис. 161).
Трапеция называется равнобедренной, если её боковые стороны равны (рис. 162, а).
Трапеция, один из углов которой прямой, называется прямоугольной (рис. 162, б).
Задачи
371. Докажите, что выпуклый четырёхугольник ABCD является параллелограммом, если:
a) ∠BAC = ∠ACD и ∠BCA = ∠D АС;
б) АВ || CD, ∠A = ∠C.
372. Периметр параллелограмма равен 48 см.
Найдите стороны параллелограмма, если:
а) одна сторона на 3 см больше другой;
б) разность двух сторон равна 7 см;
в) одна из сторон в два раза больше другой.
373. Периметр параллелограмма ABCD равен 50 см, ∠C = 30°, а перпендикуляр ВН к прямой CD равен 6,5 см. Найдите стороны параллелограмма.
374. Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке К. Найдите периметр этого параллелограмма, если ВК = 15 см, КС = 9 см.
375. Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см.
376. Найдите углы параллелограмм: ABCD, если:
a) ∠A = 84°;
б) ∠A — ∠B = 55°;
в) ∠A+∠C = 142°б
д) ∠CAD = 16°, ∠ACD = 37°.
377. В параллелограмме MNPQ проведён перпендикуляр NH к прямой MQ, причём точка Н лежит на стороне MQ. Найдите стороны и углы параллелограмма, если известно, что МН = 3 см, HQ = 5 см, ∠MNH = 30°.
378. Докажите, что параллелограмм является выпуклым четырёхугольником.
Рассмотрим параллелограмм ABCD (см. рис. 157) и докажем, что он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины. Возьмём, например, прямую АВ. Отрезок CD не имеет общих точек с прямой АВ, так как АВ || CD. Значит, этот отрезок лежит по одну сторону от прямой АВ. Но тогда и отрезки ВС и AD лежат по ту же сторону от прямой АВ. Таким образом, параллелограмм ABCD лежит по одну сторону от прямой АВ.
379. Из вершин В и D параллелограмма ABCD, у которого АВ ≠ ВС и угол А острый, проведены перпендикуляры ВК и DM к прямой АС. Докажите, что четырёхугольник BMDK — параллелограмм.
380. На сторонах АВ, ВС, CD и DA четырёхугольника ABCD отмечены соответственно точки М, N, Р и Q так, что АМ = СР, BN = DQ, BM = DP, NC = QA. Докажите, что ABCD и MNPQ — параллелограммы.
381. На рисунке 163 изображены два одинаковых колеса тепловоза. Радиусы О1А и О2В равны. Стержень АВ, длина которого равна расстоянию О1О2 между центрами колёс, передаёт движение от одного колеса к другому. Докажите, что отрезки АВ и О1О2 либо параллельны, либо лежат на одной прямой.
382. Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырёхугольник A1B1C1D1, вершинами которого являются середины отрезков ОА, ОВ, ОС и OD, — параллелограмм.
383. На диагонали BD параллелограмма ABCD отмечены две точки Р и Q так, что РВ = QD. Докажите, что четырёхугольник APCQ — параллелограмм.
384. Через середину М стороны АВ треугольника АВС проведена прямая, параллельная стороне ВС. Эта прямая пересекает сторону АС в точке N. Докажите, что AN = NC.
Через точку С проведём прямую, параллельную прямой АВ, и обозначим буквой D точку пересечения этой прямой с прямой MN (рис. 164). Так как AM = МВ по условию, а МВ = CD как противоположные стороны параллелограмма BCDM, то AM = DC. Треугольники AMN и CDN равны по второму признаку равенства треугольников (AM = CD, ∠1=∠2 и ∠3 = ∠4 как накрест лежащие углы при пересечении параллельных прямых АВ и CD секущими АС и MD), поэтому AN = NC.
385. Докажите теорему Фалеса 1 : если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Пусть на прямой l1 отложены равные отрезки А1А2, А2А3, А3А4, . и через их концы проведены параллельные прямые, которые пересекают прямую l2 в точках В1, В2, В3, В4, . (рис. 165). Требуется доказать, что отрезки В1В2, В2В3, В3В4, . равны друг другу. Докажем, например, что В1В2 = В2В3.
Рассмотрим сначала случай, когда прямые l1, и l2 параллельны (рис. 165, а). Тогда A1А2 = В1В2 и А2А3 = В2В3 как противоположные стороны параллелограммов А1В1В2А2 и А2В2В3А3. Так как А1А2 = А2А3, то и В1В2 = В2В3. Если прямые l1 и l2 не параллельны, то через точку В1 проведём прямую l, параллельную прямой l1 (рис. 165, б). Она пересечёт прямые А2В2 и А3В3 в некоторых точках С и D. Так как А1А2 = А2А3, то по доказанному B1C = CB. Отсюда получаем: B1B2 = B1B3 (задача 384). Аналогично можно доказать, что В2В3 = В3В4 и т. д.
386. Докажите, что отрезок, соединяющий середины боковых сторон трапеции, параллелен основаниям трапеции.
387. Найдите углы В и В трапеции ABCD с основаниями AD и ВС, если ∠A = 36°, ∠C =117°.
388. Докажите, что в равнобедренной трапеции: а) углы при каждом основании равны; б) диагонали равны.
389. Докажите, что трапеция равнобедренная, если: а) углы при основании равны; б) диагонали трапеции равны.
390. Один из углов равнобедренной трапеции равен 68°. Найдите остальные углы трапеции.
391. Докажите, что из одинаковых плиток, имеющих форму равнобедренной трапеции, можно сделать паркет, полностью покрывающий любую часть плоскости.
392. Основания прямоугольной трапеции равны а и b, один из углов равен α. Найдите: а) большую боковую сторону трапеции, если а = 4см, b = 7см, α = 60°; б) меньшую боковую сторону трапеции, если а = 10 см, b = 15 см, α = 45°.
393. Постройте параллелограмм: а) по двум смежным сторонам и углу между ними; б) по двум диагоналям и углу между ними; в) по двум смежным сторонам и соединяющей их концы диагонали.
в) Даны три отрезка M1N1, M2N2, M3N3 (рис. 166, а). Требуется построить параллелограмм ABCD, у которого смежные стороны, скажем АВ и AD, равны соответственно отрезкам M1N1 и M2N2, а диагональ BD равна отрезку M3N3. Проведём решение задачи по схеме, описанной на с. 94.
Допустим, что искомый параллелограмм ABCD построен (рис. 166, б). Мы видим, что стороны треугольника ABD равны данным отрезкам M1N1, M2N2 и M3N3. Это обстоятельство подсказывает следующий путь решения задачи: сначала нужно построить по трём сторонам треугольник ABD, а затем достроить его до параллелограмма ABCD.
Строим треугольник ABD так, чтобы его стороны АВ, AD и BD равнялись соответственно отрезкам M2N2 и M3N3 (как это сделать, мы знаем из курса 7 класса). Затем построим прямую, проходящую через точку В параллельно AD, и вторую прямую, проходящую через точку D параллельно АВ (как это сделать, мы также знаем из курса 7 класса). Точку пересечения этих прямых обозначим буквой С (рис. 166, в). Четырёхугольник ABCD и есть искомый параллелограмм.
По построению АВ || CD и ВС || AD, поэтому ABCD — параллелограмм. Смежные стороны параллелограмма ABCD по построению равны отрезкам и M2N2, а диагональ BD равна отрезку M3N3, т. е. параллелограмм ABCD — искомый.
Ясно, что если по трём данным отрезкам M1N1, M2N2 и M3N3 можно построить треугольник ABD, стороны которого равны этим отрезкам, то можно построить и параллелограмм ABCD. Но треугольник ABD можно построить не всегда. Если какой-то из трёх данных отрезков больше или равен сумме двух других, то треугольник ABD, а значит, и параллелограмм ABCD построить нельзя. Попробуйте самостоятельно доказать, что если задача имеет решение, то это решение единственно (см. п. 39).
394. Даны три точки А, B и С, не лежащие на одной прямой. Постройте параллелограмм так, чтобы три его вершины совпадали с данными точками. Сколько таких параллелограммов можно построить?
395. Даны острый угол hk и два отрезка P1Q1 и P2Q2. Постройте параллелограмм ABCD так, чтобы расстояние между параллельными прямыми АВ и DC равнялось P1Q1, AB = P2Q2 и ∠A = ∠ hk.
396. Разделите данный отрезок АВ на n равных частей.
Проведём луч АХ, не лежащий на прямой АВ, и на нём от точки А отложим последовательно n равных отрезков АА1, А1А2, . Аn-1Аn (рис. 167), т. е. столько равных отрезков, на сколько равных частей нужно разделить данный отрезок АВ (на рисунке 167 п = 5). Проведём прямую АnB (точка Аn — конец последнего отрезка) и построим прямые, проходящие через точки А1, А2, . Аn-1 и параллельные прямой АпВ. Эти прямые пересекают отрезок АВ в точках В1 В2, . Bn-1 которые по теореме Фалеса (задача 385) делят отрезок АВ на n равных частей.
397. Постройте равнобедренную трапецию ABCD:
а) по основанию AD, углу А и боковой стороне АВ;
б) по основанию ВС, боковой стороне АВ и диагонали BD.
398. Постройте прямоугольную трапецию ABCD по основаниям и боковой стороне AD, перпендикулярной к основаниям.
Ответы к задачам
372. а) 10,5 см, 13,5 см; б) 8,5 см, 15,5 см; в) 8 см, 16 см.
373. 13 см, 12 см, 13 см, 12 см.
375. 56 см или 70 см.
376. a) ∠B = ∠B = 96°, ∠C = 84°; б) ∠А = ∠C = 117°30′; ∠B = ∠D= 62°30′; в) ∠A = ∠C = 71°, ∠B = ∠D =109°; г) ∠A = ∠C = 120°, ∠B = ∠D = 60°; д) ∠A = ∠C= 53°, ∠B = ∠D = 127°.
377. MN = PQ = 6 cm, NP = QM = 8cm, ∠M = ∠P = 60°, ∠N = ∠Q = 120°.
379. Указание. Сначала доказать, что BK = DM.
380. Указание. Воспользоваться признаком 2 0 , п. 44.
382. Указание. Воспользоваться признаком 3 0 , п. 44.
383. Указание. Воспользоваться признаком 2 0 , п. 44.
386. Указание. Через середину боковой стороны провести прямую, параллельную основаниям, и воспользоваться задачей 385.
387. ∠B= 144°, ∠D = 63°. 388. Указание. а) Через один из концов меньшего основания провести прямую, параллельную боковой стороне.
389. Указание, а) Воспользоваться указанием к задаче 388, а; б) через один из концов меньшего основания провести прямую, параллельную диагонали.
390. 68°, 112°, 112°. Указание. Воспользоваться задачей 388, а.
391. Указание. Приложить плитки друг к другу так, чтобы боковые стороны совпали, меньшее основание одной плитки лежало на одной прямой с большим основанием другой плитки.
392. а) 6 см; б) 5см.
395. Указание. Воспользоваться задачей 284.
1 Фалес Милетский — древнегреческий учёный (ок. 625—547 гг. до н. э.).
Видео:№383 На диагонали BD параллелограмма ABCD отмечены две точки Р и Q так, что PB=QD. ДокажитеСкачать

Урок «Четырёхугольники. Решение задач»
Видео:№1039. Диагонали квадрата ABCD пересекаются в точке О. Найдите угол между векторами: а) АВ и АССкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»
Сертификат и скидка на обучение каждому участнику
Видео:Четырехугольники. Вебинар | МатематикаСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Описание слайда:
Описание слайда:
МНОГОУГОЛЬНИК
Рассмотрим фигуру, составленную из отрезков АВ, ВС, CD, . EF, FA так, что смежные отрезки (т. е. отрезки АВ и ВС, ВС и CD, . FA и АВ) не лежат на одной прямой, а несмежные отрезки не имеют общих точек. Такая фигура называется многоугольником (рис. 1). Точки А, В, С, . Е, F называются вершинами, а отрезки АВ, ВС, CD, . EF, FA — сторонами многоугольника. Сумма длин всех сторон называется периметром многоугольника.
Многоугольник с п вершинами называется n-угольником; он имеет n сторон. Примером многоугольника является треугольник. На рисунке 2 изображены четырехугольник ABCD и шестиугольник A1A2A3A4A5A6.
МНОГОУГОЛЬНИКИ
А
В
С
D
E
F
Рис. 1
А
А6
А1
А2
А3
А4
А5
В
С
D
Рис. 2
Описание слайда:
Фигура, изображенная на рисунке 3, не является многоугольником, так как несмежные отрезки С1С5 и С2С3 (а также С3С4 и С1С5) имеют общую точку.
С1
С5
С4
С3
С2
Рис. 3
Описание слайда:
Две вершины многоугольника, принадлежащие одной стороне, называются соседними. Отрезок, соединяющий любые две несоседние вершины, называется диагональю многоугольника.
Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней, а другая — внешней областью многоугольника.
На рисунке 4 внутренние области многоугольников закрашены. Фигуру, состоящую из сторон многоугольника и его внутренней области, также называют многоугольником.
Рис. 4
Описание слайда:
Выпуклый многоугольник
Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
На рисунке 5 многоугольник F1 является выпуклым, а многоугольник F2 — невыпуклым. Рассмотрим выпуклый n-угольник, изображенный на рисунке 6, а. Углы АпА1А2, A1A2A3, …, An-1AnA1 называются углами этого многоугольника. Найдем их сумму.
F1
F2
Рис. 5
A1
An
An-1
A3
A2
Рис. 6 (a)
Описание слайда:
Выпуклый многоугольник
Для этого соединим диагоналями вершину А1 с другими вершинами. В результате получим п—2 треугольника (рис. 6, б), сумма углов которых равна сумме углов n-угольника. Сумма углов каждого треугольника равна 180°, поэтому сумма углов многоугольника А1А2 …Ап равна (п -2) • 180°.
Итак, сумма углов выпуклого n-угольника равна (n—2) • 180°.
Описание слайда:
Четырёхугольник
Каждый четырехугольник имеет четыре вершины, четыре стороны и две диагонали (рис. 7). Две несмежные стороны четырехугольника называются противоположными. Две вершины, не являющиеся соседними, также называются противоположными.
Четырехугольники бывают выпуклые и невыпуклые. На рисунке 156, а изображен выпуклый четырехугольник, а на рисунке 7, б — невыпуклый.
Каждая диагональ выпуклого четырехугольника разделяет его на два треугольника. Одна из диагоналей невыпуклого четырехугольника также разделяет его на два треугольника (см. рис. 7, б).
Так как сумма углов выпуклого n-угольника равна (n—2) • 180°, то сумма углов выпуклого четырехугольника равна 360°.
Рис. 7
а)
б)
A1
A2
A3
A4
A1
A2
A3
A4
Описание слайда:
Параллелограмм
Определение
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
На рис. 8 изображен параллелограмм ABCD: AB||CD, AD||ВС. Параллелограмм является выпуклым четырехугольником.
Рассмотрим некоторые свойства параллелограмма.
1°. В параллелограмме противоположные стороны равны и противоположные углы равны.
Рассмотрим параллелограмм ABCD (рис. 9). Диагональ АС разделяет его на два треугольника: ABC и ADC. Эти треугольники равны по стороне и двум прилежащим углам (АС — общая сторона, ے1=ے2 и ے3=ے4 как накрест лежащие углы при пересечении секущей АС параллельных прямых АВ и CD, AD и ВС соответственно). Поэтому AB = CD, AD = BC и ےB=ےD. Далее, пользуясь равенствами углов 1 и 2, 3 и 4, получаем ےA= ے1 + ے3 = ے2 + ے4= ےC.
A
B
C
D
A
B
C
D
Рис. 8
Рис. 9
1
3
2
4
Описание слайда:
2°. Диагонали параллелограмма точкой пересечения делятся пополам.
Пусть О — точка пересечения диагоналей АС и BD параллелограмма ABCD (рис. 10). Треугольники АОВ и COD равны по стороне и двум прилежащим углам (AB = CD как противоположные стороны параллелограмма, L1=L2 и L3=L4 как накрест лежащие углы при пересечении параллельных прямых АВ и CD секущими АС и BD соответственно). Поэтому АО=ОС и OB = OD, что и требовалось доказать.
Рисунок 11 иллюстрирует все рассмотренные свойства.
A
B
C
D
O
1
2
4
3
Рис. 10
Рис. 11
Описание слайда:
Признаки параллелограмма
Рассмотрим три признака параллелограмма.
1°. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник—параллелограмм.
Пусть в четырехугольнике ABCD стороны АВ и CD параллельны и AB = CD (см. рис. 12).
Проведем диагональ АС, разделяющую данный четырехугольник на два треугольника: ABC и CDA. Эти треугольники равны по двум сторонам и углу между ними (АО — общая сторона, AB=CD по условию, ے1=ے2 как накрест лежащие углы при пересечении параллельных прямых АВ и CD секущей АС), поэтому ے3=ے4. Но углы 3 и 4 накрест лежащие при пересечении прямых AD и ВС секущей АС, следовательно, AD||ВС.
Таким образом, в четырехугольнике ABCD противоположные стороны попарно параллельны, и, значит, четырехугольник ABCD — параллелограмм.
A
B
C
D
Рис. 12
1
3
4
2
Описание слайда:
2°. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Проведем диагональ АС данного четырехугольника ABCD, разделяющую его на треугольники ABC и CDA (см. рис. 13). Эти треугольники равны по трем сторонам (АС — общая сторона, AB = CD и BC=DA по условию), поэтому L1 =L2. Отсюда следует, что АВ||CD. Так как AB = CD и AB||CD, то по признаку 1° четырехугольник ABCD — параллелограмм.
3°. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся
пополам, то этот четырехугольник — параллелограмм.
Рассмотрим четырехугольник ABCD, в котором диагонали АС и BD пересекаются в точке О и делятся этой точкой пополам (см. рис. 14). Треугольники АОВ и COD равны по первому признаку равенства треугольников (АО = ОС, BO = OD по условию, ےAOB = ےCOD как вертикальные углы, поэтому АВ = CD и ےl = ے2. Из равенства углов 1 и 2 следует, что АВ || CD.
Итак, в четырехугольнике ABCD стороны АВ и CD равны и параллельны, значит, по признаку 1° четырехугольник ABCD — параллелограмм.
A
B
C
D
Рис. 13
A
B
C
D
O
1
2
4
3
Рис. 14
1
3
2
4
Описание слайда:
Трапеция
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны трапеции называются ее основаниями, а две другие стороны — боковыми сторонами (рис. 15).
Трапеция называется равнобедренной, если ее боковые стороны равны (рис. 16, а). Трапеция, один из углов которой прямой, называется прямоугольной (рис. 16, б).
Равнобедренная трапеция
а)
Прямоугольная трапеция
б)
Рис. 16
Основание
Боковая сторона
Основание
Боковая сторона
Рис. 16
Описание слайда:
Теорема ФАЛЕСА
Докажем теорему Фалеса: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Решение.
Пусть на прямой L1 отложены равные отрезки A1A2, A2A3, A3A4 и через их концы проведены параллельные прямые, которые пересекают прямую L2 в точках B1, B3, B4, . (рис. 17). Требуется доказать, что отрезки B1B2, B2B3, B3B4, … равны друг другу. Докажем, например, что B1B2=B3B4. Рассмотрим сначала случай, когда прямые L1 и L2 параллельны (рис. 17, а). Тогда А1А2=В1В2 и А2A3=B2B3 как противоположные стороны параллелограммов A1B1B2A2 и A2B2B3A3. Так как A1A2=A2A3, то и B1B2=B2B3. Если прямые L1 и L2 не параллельны, то через точку B1 проведем прямую L, параллельную прямой L1 (рис. 17, б). Она пересечет прямые А2В2 и A3B3 в некоторых точках С и D. Так как А1А2=А2А3, то по доказанному B1C=CD. Отсюда получаем В1В2=В2В3 (задача 1). Аналогично можно доказать, что B2B3=B3B4 и т. д.
Рис. 17
Описание слайда:
Прямоугольник
Прямоугольником называется параллелограмм, у которого все углы прямые.
Так как прямоугольник является параллелограммом, то он обладает всеми свойствами параллелограмма: в прямоугольнике противоположные стороны равны, а диагонали точкой пересечения делятся пополам.
Рассмотрим особое свойство прямоугольника.
Диагонали прямоугольника равны.
Действительно, обратимся к рисунку 18, на котором изображен прямоугольник ABCD с диагоналями АС и BD. Прямоугольные треугольники ACD и DBA равны по двум катетам (CD=BA, AD — общий катет). Отсюда следует, что гипотенузы этих треугольников равны, т.е. AC = BD, что и требовалось доказать.
A
B
C
D
Рис. 18
Описание слайда:
обратное утверждение (признак прямоугольника).
Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
A
B
C
D
Рис. 19
Описание слайда:
Ромб и квадрат
Ромбом называется параллелограмм, у которого все стороны равны. Так как ромб является параллелограммом, то он обладает всеми свойствами параллелограмма. Рассмотрим особое свойство ромба.
Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Рассмотрим ромб ABCD (рис. 20). Требуется доказать, что AC┴BD и каждая диагональ делит соответствующие углы ромба пополам. Докажем, например, что ےBAC=ےDAC.
По определению ромба AB=AD, поэтому треугольник BAD равнобедренный. Так как ромб — параллелограмм, то его диагонали точкой О пересечения делятся пополам. Следовательно, АО — медиана равнобедренного треугольника BAD, а значит, высота и биссектриса этого треугольника. Поэтому AC┴BD и ےBAC=ےDAC, что и требовалось доказать.
A
B
C
D
O
Рис. 20
Описание слайда:
Квадратом называется прямоугольник, у которого все стороны равны.
Прямоугольник является параллелограммом, поэтому и квадрат является параллелограммом, у которого все стороны равны, т. е. ромбом. Отсюда следует, что квадрат обладает всеми свойствами прямоугольника и ромба. Сформулируем основные свойства квадрата.
Все углы квадрата прямые (рис. 21, а).
Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам (рис. 21, б).
а)
б)
Свойства квадрата. Рис. 21
📺 Видео
№174. Найдите двугранный угол ABCD тетраэдра ABCD, если углы DAB, DAC и ACB прямые, ACСкачать

№339381 В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB Найдите меньший угол междуСкачать

№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать

Диагонали четырехугольника равны 4 и 5.Скачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

ЧЕТЫРЕХУГОЛЬНИК 8 класс РЕШЕНИЕ ЗАДАЧ АтанасянСкачать
























