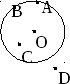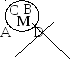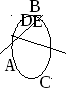Данный урок является уроком обобщения и систематизации знаний по изученной теме.В ходе урока учащиеся имеют возможность проверить свои знания по темам «Вписанный угол» и «Пропорциональность отрезков хорд и секущих окружности», решить задачи открытого банка ОГЭ.
- Просмотр содержимого документа «Тема урока «Пропорциональность отрезков хорд и секущих окружности» 9 класс»
- Окружность. Свойства отрезков пересекающихся хорд, секущих и касательных
- Презентация к уроку
- Конспект урока по геометрии на тему «Хорда»
- Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
- 🎦 Видео
Просмотр содержимого документа
«Тема урока «Пропорциональность отрезков хорд и секущих окружности» 9 класс»
Урок № ____ (геометрия 9 класс)
Пропорциональность отрезков, хорд и секущих
Цель урока: закрепить свойства отрезков пересекающихся хорд и свойства секущих отрезков и показать, как они используются при решении задач.
образовательная: проверить знания теоретического материала по темам «Углы, вписанные в окружность. Пропорциональность отрезков, хорд и секущих»
развивающая: развитие познавательного интереса, любознательности, умение анализировать, наблюдать и делать выводы;
воспитательная: повышать заинтересованность в изучении предмета математики; воспитание самостоятельности, активности.
Орг.момент (1 мин)
Проверка домашнего задания (фронтально) (3 мин.)
Актуализация опорных знаний учащихся. Фронтальная работа с классом. (7 мин.)
— Что такое окружность, центр окружности, радиус?
— Является ли радиусом этой окружности
-Что такое хорда окружности? Какая хорда называется диаметром?
— Постройте полупрямую DС. Как называется такая полупрямая?
— С какими углами, связанными с окружностью, вы уже знакомы?
— Дайте определение и назовите их на чертеже.
— Как связаны градусные меры этих углов?
— Как связаны их градусные меры с дугой, на которую они опираются?
— Какие следствия из теоремы о вписанном в окружность угле нами изучены?
-Сформулируйте свойство отрезков пересекающихся хорд окружности.
-Сформулируйте свойство отрезков секущих окружности.
Тренировочные упражнения. Решение задач (14 мин.)
Хорды МК и РТ пересекаются в точке А. Найдите длину АМ, если АР = 2 дм, АТ = 24 дм, АМ : КА = 3 : 4.
Из одной точки проведены к окружности две секущие, внутренние отрезки которых соответственно равны 8 и 16. Внешний отрезок второй секущей на 1 меньше внешнего отрезка первой. Найти длину каждой секущей.
Самостоятельная работа с взаимопроверкой (12 мин).
Центральный угол на 59 0 больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.
Центральный угол на 52 0 больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.
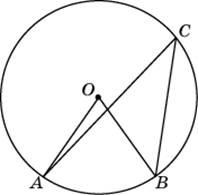
В окружности с центром O AC и BD — диаметры. Центральный угол AOD равен 138 0 . Найдите вписанный угол ACB. Ответ дайте в градусах.
2)
В окружности с центром O AC и BD — диаметры. Центральный угол AOD равен 146 0 . Найдите вписанный угол ACB. Ответ дайте в градусах.
3)
Хорды АВ и СD пересекаются в точке М. СМ=2 см, МD=6 см, ВМ=3 см. Найдите длину отрезка АМ.
3)
Хорды АВ и СD пересекаются в точке М. СМ=2 см, МD=12 см, ВМ=3 см. Найдите длину отрезка АМ.
4)
Дано: ВС=12 см. ВЕ=4 см. ВА=16 см.
4)
Видео:9 класс. Геометрия. Теорема о пропорциональности отрезков хорд и в секущих окружности. 22.05.2020.Скачать

Окружность. Свойства отрезков пересекающихся хорд, секущих и касательных
Презентация к уроку
Цель: повысить мотивацию к обучению; развивать вычислительные навыки, сообразительность, умение работать в команде.
Окружность — это линия, состоящая из всех точек плоскости, которые находятся на заданном расстоянии от одной точки плоскости, называемой центром окружности.
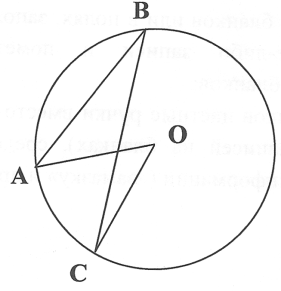
На слайде изображена окружность, отмечен ее центр — точка О, проведены два отрезка: ОА и СВ. Отрезок ОА соединяет центр окружности с точкой на окружности. Он называется РАДИУСОМ (по-латыни radius — “спица в колесе”). Отрезок СВ соединяет две точки окружности и проходит через ее центр. Это диаметр окружности (в переводе с греческого – “поперечник”).
Также нам понадобится определение хорды окружности — это отрезок, соединяющий две точки окружности (на рисунке – хорда DE).
Давайте выясним вопрос о взаимном расположении прямой и окружности.
Следующий вопрос и он будет основным: выяснить свойства, которыми обладают пересекающиеся хорды, секущие и касательные.
Доказывать эти свойства вы будете на уроках математики, а наша задача научиться применять эти свойства при решении задач, так как они находят широкое применение на экзаменах и в форме ЕГЭ, и в форме ГИА.
Задание для команд.
Далее продолжим работать в парах над решением простейших задач по применению этих свойств:
Используя данные на рисунке, найдите х. Слайд 5–6
Кто быстрее, правильней. С последующим обсуждением и проверкой решения всех задач. Отвечающие зарабатывают для своей команды поощрительные баллы.
Ну, а теперь приступим к решению более серьезных задач. Вашему вниманию предлагается три блока: пересекающиеся хорды, касательная и секущая, две секущие. Подробным образом разберем решение по одной задачи из каждого блока.
(Разбирается решение с подробной записью №4, №7, №12)
2. Практикум по решению задач
а) Пересекающиеся хорды
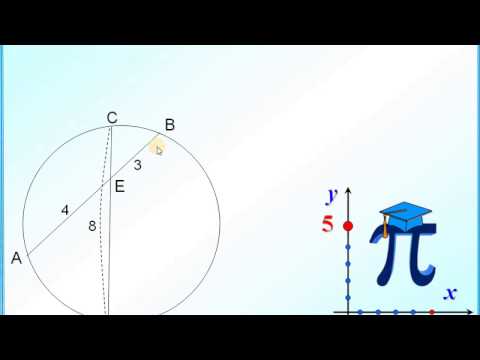
1. E – точка пересечения хорд AB и CD. AE=4, AB=10, СE:ED=1:6. Найти CD.
Решение:
2. E – точка пересечения хорд AB и CD. AB=17, CD=18, ED=2CE. Найти AE и BE.
Решение:
3. E – точка пересечения хорд AB и CD. AB=10, CD=11, BE=CE+1. Найти CE.
Решение:
4. E – точка пересечения хорд AB и CD. ED=2AE, CE=DE-1, BE=10. Найти CD.
Решение:
б) Касательная и секущая
5. Из одной точки проведены к окружности касательная и секущая. Касательная равна 6, секущая – 18. Определить внутренний отрезок секущей.
Решение:
6. Из одной точки проведены к окружности касательная и секущая. Найти касательную, если известно, что она меньше внутреннего отрезка секущей на 4 и больше внешнего отрезка на 4.
Решение:
7. Из одной точки проведены к окружности касательная и секущая. Найти секущую, если известно, что внутренний её отрезок относится к внешнему, как 3:1, а длина касательной равна 12.
Решение:
8. Из одной точки проведены к окружности касательная и секущая. Найти внешний отрезок, секущей, если известно, что внутренний её отрезок 12, а длина касательной 8.
Решение:
9. Касательная и секущая, исходящие из одной точки, соответственно равны 12 и 24. Определить радиус окружности, если секущая удалена от центра на 12.
Решение:
10. Из одной точки проведены к окружности две секущие, внутренние отрезки которых соответственно равны 8 и 16. Внешний отрезок второй секущей на 1 меньше внешнего отрезка первой. Найти длину каждой секущей.
Решение:
11. Из одной точки проведены к окружности две секущие. Внешний отрезок первой секущей относится к своему внутреннему, как 1:3. Внешний отрезок второй секущей на 1 меньше внешнего отрезка первой и относится к своему внутреннему отрезку, как 1:8. Найти длину каждой секущей.
Решение:
12. Через точку А, которая находится вне окружности на расстоянии 7 от её центра, проведен прямая, пересекающая окружность в точках В и С. Найдите длину радиуса окружности, если АВ=3, ВС=5.
Решение:
13. Из точки А проведены к окружности секущая длиной 12 см и касательная, составляющая 
Решение:
3. Закрепление знаний
Считаю, что вы обладаете достаточным запасом знаний, чтобы отправится в небольшое путешествие по лабиринтам вашего интеллекта, посетив следующие станции:
- Соображай-ка!
- Решай-ка!
- Отвечай-ка!
На станции можно находиться не более 6 минут. За каждое верное решение задачи команда получает поощрительные баллы.
Командам вручаются маршрутные листы:
| Станция | Номера задач | Отметка о решении |
| Решай-ка! | №1, №3 | |
| Соображай-ка! | №5, №8 | |
| Отвечай-ка! | №10, №11 |
| Станция | Номера задач | Отметка о решении |
| Соображай-ка! | №5, №8 | |
| Отвечай-ка! | №10, №11 | |
| Решай-ка! | №1, №3 |
| Станция | Номера задач | Отметка о решении |
| Соображай-ка! | №5, №8 | |
| Отвечай-ка! | №10, №11 | |
| Решай-ка! | №1, №3 |
4. Подведение итогов
Хотелось бы подвести итоги нашего занятия:
Помимо новых знаний надеюсь, вы лучше познакомились друг с другом, приобрели опыт работы в команде. А как вы думаете, полученные знания находят где-то применение в жизни?
Поэт Г. Лонгфелло был еще и математиком. Наверное, поэтому яркие образы, украшающие математические понятия, которые он использовал в своем романе “Каванг”, позволяют запечатлеть на всю жизнь некоторые теоремы и их применение. Читаем в романе следующую задачу:
“Лилия, на одну пядь поднимавшаяся над поверхностью воды, под порывом свежего ветра коснулась поверхности озера в двух локтях от прежнего места; исходя из этого требовалось определить глубину озера” (1 пядь равна 10 дюймам, 2 локтя – 21 дюйму).
А решается эта задача на основе свойства пересекающихся хорд. Посмотрите на рисунок, и станет ясно, как находится глубина озера.
Видео:Пропорциональность отрезков хорд, касательных и секущих. Геометрия 9 классСкачать

Конспект урока по геометрии на тему «Хорда»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:Теорема об отрезках хорд и секущихСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Сертификат и скидка на обучение каждому участнику
Поурочный план по геометрии
Тема: Пропорциональность отрезков хорд и секущих окружности
Цель урока: закрепить свойства отрезков пересекающихся хорд и свойства секущих отрезков и показать, как они используются при решении задач.
Актуализация знаний. Сегодня мы продолжим говорить об окружности. Позвольте напомнить определение окружности: что называется окружностью?
Окружность — это линия, состоящая из всех точек плоскости, которые находятся на заданном расстоянии от одной точки плоскости, называемой центром окружности.
На слайде изображена окружность, отмечен ее центр — точка О, проведены два отрезка: ОА и СВ. Отрезок ОА соединяет центр окружности с точкой на окружности. Он называется РАДИУСОМ (по-латыни radius — “спица в колесе”). Отрезок СВ соединяет две точки окружности и проходит через ее центр. Это диаметр окружности (в переводе с греческого – “поперечник”).
Также нам понадобится определение хорды окружности — это отрезок, соединяющий две точки окружности (на рисунке – хорда DE).
Давайте выясним вопрос о взаимном расположении прямой и окружности.
Следующий вопрос и он будет основным: выяснить свойства, которыми обладают пересекающиеся хорды, секущие
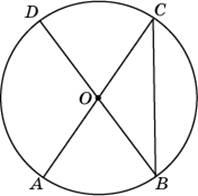
Если хорды АВ и CD окружности пересекаются в точке S, то AS . BS=CS . DS.
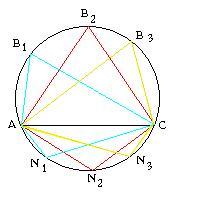
Докажем сначала, что треугольники ASD и CSB подобны (рис. 2,29). Вписанные углы DCB и DAB равны по следствию из теоремы 17. Углы ASD и BSC равны как вертикальные. Из равенства указанных углов следует, что треугольники ASD и CSB подобны.
Из подобия треугольников следует пропорция
Отсюда AS . BS=CS . DS что и требовалось доказать.

Если из точки Р к окружности проведены две секущие, пересекающие окружность в точках А, В и С, D соответственно, то AP . BP=CP . DP.
Пусть точки А и C — ближайшие к точке Р точки пересечения секущих с окружностью (рис. 252). Треугольники PAD и РСВ подобны. У них угол при вершине Р обпщй, а углы при вершинах Ви D равны по свойству углов, вписанных в окружность. Из подобия треугольников следует пропорция
Отсюда PA . PB=PC . PD, что и требовалось доказать.
Доказать, что если хорды АВ и CD окружности пересекаются в точке S, то AS*BS = CS*DS.
Доказательство. Докажем сначала, что треугольники ASD и CSB подобны (рис.1).
Вписанные углы DCB и DAB равны по следствию 1. Углы ASD и BSC равны как вертикальные. Из равенства указанных углов следует, что треугольники ASD и С SB подобны.
Из подобия треугольников следует пропорция
Отсюда AS•BS = CS•DS ,что и требовалось доказать.
1) если из точки Р (рис.2), лежащей вне окружности, проведены к ней две секущие, пересекающие окружность в точках А, В и С, D соответственно, то AP•BP = CP•DP
2) если из точки Р (рис.3), лежащей вне окружности, проведены к ней секущая, пересекающая окружность в точках А и Б, и касательная PC, то РА•РВ = РС 2 .
Пример 1. Хорды АВ и CD пересекаются в точке Е. Найти ED, если АЕ = 5 см, BE = 2 см, СЕ = 2,5 см.
Решение. Имеем: АЕ • BE = ED • СЕ (задача), или откуда5•2=2,5•ED , откуда ED=102,5=10025=4 (см).
Пример 2 . Из точки А, лежащей вне окружности, проведены две секущие. Внутренний отрезок первой равен 47 м, а внешний 9 м; внутренний отрезок второй секущей на 72 м больше внешнего ее отрезка. Найти внешний отрезок второй секущей.
Решение. Обозначим через х длину внешнего отрезка второй секущей. Тогда согласно условию задачи длина внутреннего отрезка второй секущей будет х + 72. Теперь согласно утверждению 1) имеем:
Решая это уравнение, находим х = 6.
Пример 3. Из точки Р проведены к окружности касательная PC = 12 м и секущая РВ = 16 м. Найти внешнюю часть секущей АР.
Решение. Обозначим через х длину внешнего отрезка секущей. Тогда согласно утверждению 2) имеем:
Пропорциональность отрезков хорд и секущих окружности
Задача 1. Доказать, что если хорды АВ и CD окружности пересекаются в точке S, то AS*BS = CS*DS.
Доказательство. Докажем сначала, что треугольники ASD и CSB подобны (рис.1).
Вписанные углы DCB и DAB равны по следствию 1. Углы ASD и BSC равны как вертикальные. Из равенства указанных углов следует, что треугольники ASD и С SB подобны.
Из подобия треугольников следует пропорция
Отсюда AS•BS = CS•DS ,что и требовалось доказать.
1) если из точки Р (рис.2), лежащей вне окружности, проведены к ней две секущие, пересекающие окружность в точках А, В и С, D соответственно, то AP•BP = CP•DP
2) если из точки Р (рис.3), лежащей вне окружности, проведены к ней секущая, пересекающая окружность в точках А и Б, и касательная PC, то РА•РВ = РС 2 .
Пример 1 . Хорды АВ и CD пересекаются в точке Е. Найти ED, если АЕ = 5 см, BE = 2 см, СЕ = 2,5 см.
Решение. Имеем: АЕ • BE = ED • СЕ (задача), или откуда5•2=2,5•ED , откуда ED=102,5=10025=4 (см).
Стр.76-77 выучитьтеорему17, задача№200-203 стр.77
🎦 Видео
Пропорциональные отрезки круга. 9 класс.Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Пропорциональные отрезки в окружности. Практическая часть. 9 класс.Скачать
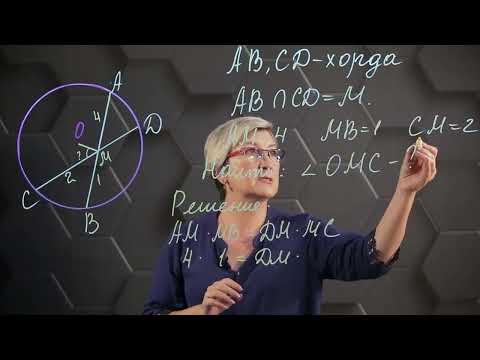
Свойства отрезков хорд, касательных и секущих. Решение задач.Скачать

Теорема о произведении отрезков пересекающихся хорд.Скачать

Свойства хорд, касательных, секущих окружности I Для решения задач из ОГЭ И ЕГЭ I Часть 1Скачать

#234. Формула Эйлера | Свойства отрезков хорд и секущихСкачать

Окружность №16 из ОГЭ. Свойства хорд, касательных, секущих.Скачать

теорема о произведении отрезков секущихСкачать

Секущая и касательная. 9 класс.Скачать

Секретная теорема из учебника геометрииСкачать

Математика ОГЭ Задание 24 Отрезки пересекающихся хордСкачать
Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

Геометрия. 9 класс. Теоремы о пропорциональности отрезков в окружности /15.04.2021/Скачать

ЕГЭ математика 2021: Все задачи на Секущие, хорды и касательные (6 задание)Скачать

Свойства отрезков, хорд, секущих и касательных.Скачать