В окружности радиуса 6 см проведена хорда ав

Видео:№1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать

Ваш ответ

Видео:Геометрия В окружность, радиус которой равен 8 см, проведена хорда AB. На прямой AB вне отрезка ABСкачать

решение вопроса

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,022
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Радиус Хорда ДиаметрСкачать

. В окружности радиуса 6 см проведена хорда АВ?

Геометрия | 10 — 11 классы

. В окружности радиуса 6 см проведена хорда АВ.

Через середину М этой хорды проходит прямая, пересекающая окружность в точках С и Е.

Известно, что СМ = 9 см, &lt ; АСВ = 30°.

Найдите длину отрезка СЕ.

Пусть точка О — центр окружности.

Угол АСВ — вписанный угол опирающийся на дугу АВ, значит он равен 1 / 2 дуги ВС, следовательно градусная мера дуги ВС = 2 * АСВ = 2 * 30 = 60 * .

Угол АОВ — центральный опирающийся на дугу АВ, значит он равен градусной мере дуги АВ, т.

Треугольник АОВ — равнобедренный (АО = ОВ — как радиусы), значит угол ОАВ = углу ОВА = (180 — 60) : 2 = 60 * , следовательно треугольник АОВ и равносторонний, значит АВ = ОВ = 6см.

Тогда АМ = МВ = 6 : 2 = 3см.

По теореме об отрезках пересекающихся хорд имеем : МЕ = (АМ * МВ) : МС = 3 * 3 : 9 = 1см.

Значит СЕ = 9 + 1 = 10см.

ОТВЕТ : СЕ = 10см.

Видео:Радиус и диаметрСкачать

Из точки на окружности проведены две хорды 5 см?

Из точки на окружности проведены две хорды 5 см.

Длина отрезка соединяющего их середины равна 6 см.

Найти радиус окружности.

Видео:Геометрия В окружности проведены диаметр AC и хорда AB равная радиусу окружности Найдите углыСкачать

В окружности радиуса 6 см проведена хорда АВ?

В окружности радиуса 6 см проведена хорда АВ.

Через середину М этой хорды проходит прямая, пересекающая окружность в точках С и Е.

Известно, что СМ = 9 см, &lt ; АСВ = 30°.

Найдите длину отрезка СЕ.

Видео:Геометрия В окружности, радиус которой равен 10 см, проведена хорда длиной 16 см. Найдите расстояниеСкачать

Радиус ОВ окружности с центром О пересекает хорду MN в ее середине, точке K?

Радиус ОВ окружности с центром О пересекает хорду MN в ее середине, точке K.

Найдите длину хорды MN, если КВ = 1 см, а радиус равен 13.

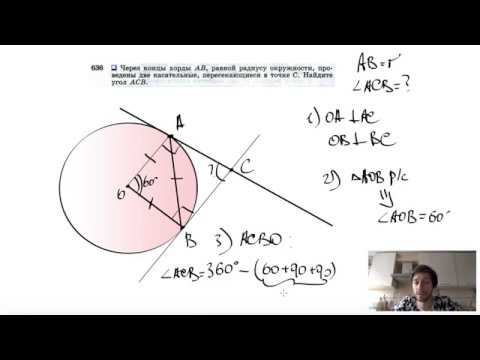
Видео:№636. Через концы хорды АВ, равной радиусу окружности, проведены две касательные, пересекающиесяСкачать

Радиус OB окружности с центром в точке O пересекает хорду MN в её середине – точке K?

Радиус OB окружности с центром в точке O пересекает хорду MN в её середине – точке K.

Найдите длину хорды MN, если KB = 1 см, а радиус окружности равен 13 см.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Радиус OB окружности с центром в точке O пересекает хорду MN в ее середине — точке K?

Радиус OB окружности с центром в точке O пересекает хорду MN в ее середине — точке K.

Найдите длину хорды MN если KB = 1 см, а радиус окружности равен 13 см.

Видео:№635. Через точку А окружности проведены касательная и хорда, равная радиусу окружности.Скачать

В окружности с радиусом 10 см проведена хорда AB длиной 16 см?

В окружности с радиусом 10 см проведена хорда AB длиной 16 см.

Касательные к окружности проведенные через точки A и B, пересекаются в точке C.

Найдите длинну отрезка AC.

Видео:№666. Хорды АВ и CD пересекаются в точке Е. Найдите ED, если: а) АЕ = 5, ВЕСкачать

Через концы хорды АВ, равной радиусу окружности, проведены две касательные, пересекающиеся в точке С?

Через концы хорды АВ, равной радиусу окружности, проведены две касательные, пересекающиеся в точке С.

Найдите угол АСВ.

Видео:ЕГЭ-2022 ||Задание №6 || Найти длину хордыСкачать

ПОМОГИТЕ ПЛИЗ?

Из точки на окружность проведены две хорды длиной 10 и 12см.

Известно что от середины меньшей хорды до большой хорды равно 4см.

Найти радиус окружности.

Видео:Геометрия В окружности проведены хорды AB и CD, пересекающиеся в точке M. Дано: AM/МВ =5/7Скачать

Окружности радиус 15 см проведена хорда длиной 18 см найдите расстояние от центра окружности к даной хорде?

Окружности радиус 15 см проведена хорда длиной 18 см найдите расстояние от центра окружности к даной хорде.

Видео:Задача 6 №27859 ЕГЭ по математике. Урок 104Скачать

В окружности радиусом 3 с центром в точке О из точ­ки А окружности проведены две хорды, пересекающие окружность в точках В и С (см?

В окружности радиусом 3 с центром в точке О из точ­ки А окружности проведены две хорды, пересекающие окружность в точках В и С (см.

Найдите длину хорды СВ, если угол CAB = 30°.

На этой странице находится вопрос . В окружности радиуса 6 см проведена хорда АВ?, относящийся к категории Геометрия. По уровню сложности данный вопрос соответствует знаниям учащихся 10 — 11 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Геометрия. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.

Видео:№638. Прямая АВ касается окружности с центром О радиуса r в точке В. Найдите АВСкачать

Касательная к окружности

О чем эта статья:

Видео:Задача 6 №27877 ЕГЭ по математике. Урок 118Скачать

Касательная к окружности, секущая и хорда — в чем разница

В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).

Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.

Видео:Геометрия В окружности радиуса r проведена хорда, равная 0,5r. Через один конец хорды проведенаСкачать

Свойства касательной к окружности

Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.

Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

• окружность с центральной точкой А;
• прямая а — касательная к ней;
• радиус АВ, проведенный к касательной.

Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.

Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.

В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Задача

У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.

∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°

Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.

Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.

Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.

Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.

Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.

Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.

Задача 1

У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.

Решение

Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.

∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).

Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Задача 2

К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.

Решение

Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°

Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.

Задача 1

Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.

Решение

Исходя из соотношения касательной и секущей МА 2 = МВ × МС.

Найдем длину внешней части секущей:

МС = МВ — ВС = 16 — 12 = 4 (см)

МА 2 = МВ × МС = 16 х 4 = 64

Задача 2

Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА 2 = МВ × МС.

(у + R) 2 : 4 = (у + R) × (у — R)

Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Ответ: MO = 10 см.

Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.

Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.

Задача 1

Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.

АВ = ∠АВС × 2 = 32° × 2 = 64°

Задача 2

У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

КМ = 2 ∠МКВ = 2 х 84° = 168°

Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.

∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°

🌟 Видео

Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

Как Найти Радиус Сегмента на Потолке. Радиус Окружности По Хорде И Высоте СегментаСкачать

Геометрия Хорды AB и CD окружности пересекаются в точке M, AM = 6 см, BM = 14 см, CM = 12 смСкачать