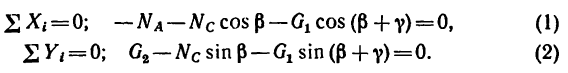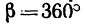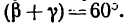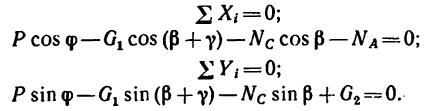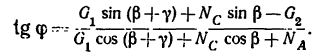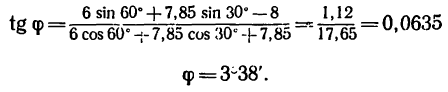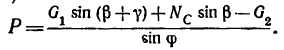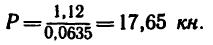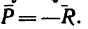Общие положения
Одним из основных, безусловно, необходимых свойств сварных металлических конструкций, как несущих сооружений, является геометрическая неизменяемость. Это означает, что в конструкции под действием внешней нагрузки не может быть взаимных перемещений элементов и частей. Иначе говоря, каждый элемент конструкции имеет степень свободы, равную нулю.
В то же время следует отметить, что под действием внешней нагрузки элементы конструкции упруго изменяют свои форму и размеры. Так, например, в ферме растянутые элементы удлиняются, а сжатые укорачиваются, а ферма в целом получает прогиб. Эти изменения представляют собой нормальное явление, происходящее со всеми твердыми телами под нагрузкой и обусловленное упругой деформацией материала. После снятия нагрузки элементы и ферма принимают исходные форму и размеры. Упругие деформации элементов реальных металлических конструкций обычно не превышают 0,1%.
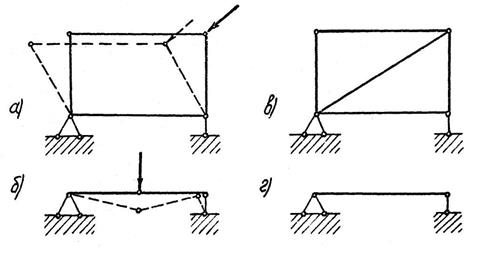
Изменяемые системы могут изменить свою форму под действием бесконечно малых нагрузок без изменения размеров элементов только за счет их взаимного перемещения. В качестве примера можно привести шарнирный четырехугольник и однопролетную балку, имеющую в пролете шарнир, (рис.3.1 а,б). Если четырехугольник раскрепить диагональным стержнем, (рис. 3.1 в), а из балки убрать шарнир (рис.3.1 г), то эти системы превратятся в геометрически неизменяемые.
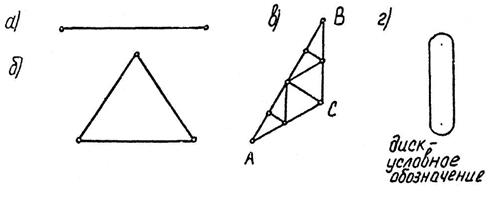
Понятие «диск». В статике сооружений диском называют такую часть системы, в геометрической неизменяемости которой нет сомнений. Простейшими дисками являются стержень и шарнирный стержневой треугольник (рис. 3.2 а, б). Ферма АВС, приведенная на рис. 3.2 б, может также рассматриваться как диск. Обобщенное изображение диска, независимо от внутренней структуры, показано на рис. 3.2 г. «Земля», как неизменяемое основание сооружения, также считается диском.
Рис. 3.1. Примеры геометрически изменяемых (а, б)
и неизменяемых (в, г) стержневых систем
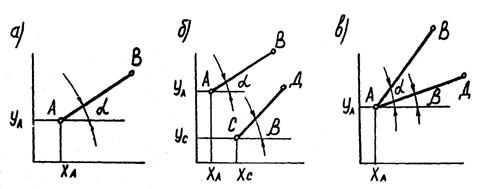
Понятие «степень свободы». В статике сооружений под степенью свободы диска понимают число геометрических параметров, которые могут изменяться независимо друг от друга при перемещении этого диска. В плоской системе координат точка имеет степень свободы, равную двум, так как ее положение определяется двумя координатами. Стержень (диск) в плоскости имеет степень свободы, равную трем, так как положение стержня определяется тремя геометрическими параметрами (ХА,УА, угол α) которые при перемещении стержня могут изменяться независимо друг от друга (рис. 3.3 а). Отсюда, следует, что число степеней свободы стержней, не связанных между собой, в плоскости равно утроенному количеству стержней. Шарнир, связывающий два стержня, снижает степень свободы системы на два (рис.3.3 в).
Рис. 3.2. Примеры дисков
Рис. 3.3. Степень свободы стержней: а — стержень в плоскости имеет 3 степени свободы; б — два отдельных стержня имеют 6 степеней свободы; в — два стержня соединенные общим шарниром имеют 4 степени свободы
Действительно, суммарное число степеней свободы двух стержней, не связанных между собой, равно шести. Если мы соединим их общим шарниром А, стержни могут перемещаться только совместно. Положение шарнира А определяется двумя координатами, которые могут изменяться независимо друг от друга. Кроме того, каждый стержень независимо один от другого может поворачиваться около шарнира А. Следовательно, степень свободы системы, приведенной на рис.3.3 в, равна четырем.
Таким образом, шарнир, соединяющий два диска, (простой шарнир) уменьшает степень свободы системы на две единицы. Если шарнир соединяет три и более дисков, его называют сложным. Если сложный шарнир соединяет N дисков, то по числу налагаемых связей он эквивалентен (N-1) простому шарниру. Каждый опорный стержень уменьшает степень свободы системы на единицу.
На основании вышеизложенного можно записать
где W — степень свободы системы; D — количество дисков; Ш— количество простых шарниров (шарниры, присоединяющие к диску только опорные стержни, в счет не входят); СОП —количество опорных стержней.
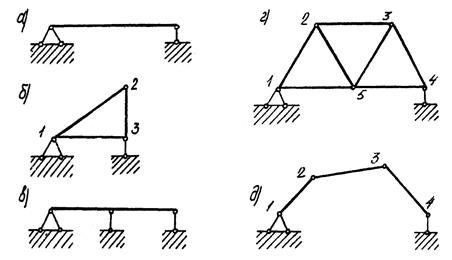
На рис. 3.4 приведены примеры стержневых систем для анализа степени свободы W.
Рис. 3.4. Примеры стержневых систем для анализа степени свободы W
Если W = 0 — система неизменяема и статически определима;
если W> 0 — система изменяема; если W = 3 ·1 — 2 · 0 -3 = 0 ; система неизменяема и статически определима.
Для системы, приведенной на рис. 4 б, D = 3; Ш = 3 (шарниры I и 3 учитываем, так как они не только присоединяют опорные стержни, но и соединяют между собой диски); СОП = 3, отсюда получаем W = 3 · 3 — 2 · 3 — 3 = 0; система неизменяема и статически определима. В данной системе шарнирный треугольник в целом также является диском, поэтому можно записать D = 1; Ш = 0; СОП = 3, получаем также W = 0.
Анализ, как мы видим, приводит к тому же результату.
Для системы, приведенной на рис. 3.4 в, D = 1; Ш = 0; СОП = 4, получаем
W = 3 ·1 — 2 · 0 — 4 = -1; система неизменяема и один раз статически неопределима.
Для системы, приведенной на рис. 3.4 г, D = 7; Ш = 9 (шарниры I и 4, соединяющие по два диска, являются простыми; шарниры 2 и 3, соединяющие по три диска, являются сложными и каждый эквивалентен 3-1 = 2 простым шарнирам; шарнир 5 эквивалентен 4 — 1= 3 простым шарнирам;
Ш = 1 + 1 + 1 + 2 + 2 + 3 = 9; СОП = 3, получаем
W = 3 · 7- 2 · 9 — 3 = 0; система неизменяема и статически определима.
Для системы, приведенной на рис. 3.4 д, D = 3; Ш = 2 (шарниры 1 и 4 служат для присоединения только опорных стержней и в счет не входят); СОП = 3, получаем W = 3 · 3- 2 · 2 — 3 = 2; система изменяема и имеет степень свободы, равную двум. Анализ изменяемости системы, не связанной опорными стержнями с землей, проводится при помощи формулы
где V — степень изменяемости системы, характеризующая взаимные перемещения элементов системы.
Если V = 0, то в системе взаимные перемещения составляющих ее элементов отсутствуют, т.е. система внутренне геометрически неизменяема.
При этом нужно иметь в виду, что система в целом может перемещаться в плоскости со степенью свободы, равной трем. Анализ на внутреннюю геометрическую неизменяемость систем, присоединенных опорными стержнями к земле, можно провести, предварительно отбросив опорные стержни. Это можно делать, если число опорных стержней СОП = 3. Если число опорных стержней СОП ≥ 4, анализ систем на геометрическую неизменяемость можно проводить только в связи с землей.
Видео:Кинематический анализ 1Скачать

Равновесие сходящихся сил в теоретической механике
Равновесие сходящихся сил:
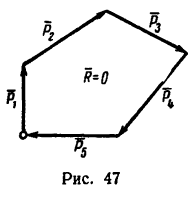
При определении равнодействующей системы пяти сил в задаче установлено, что
Из геометрического условия следует аналитическое условие равновесия, выражающееся двумя уравнениями:
Следует заметить, что все задачи, приведенные в § 6-2, можно решить с применением условия равновесия системы сходящихся сил. Причем при решении задач на равновесие системы сходящихся сил можно использовать те же три метода: графический, графо-аналитический и аналитический (метод проекций).
Необходимо учитывать, что если рассматривается равновесие плоской системы сходящихся сил, приложенных к одному телу, число неизвестных величин не должно превышать двух (условие статической определимости задачи с плоской системой сходящихся
сил):
- а) неизвестна одна сила, т. е. ее модуль и направление;
- б) неизвестны направления двух сил данной системы;
- в) неизвестны модуль одной из сил и направление второй;
- г) неизвестны модули двух сил.
При графическом методе решения во всех четырех случаях можно построить замкнутый силовой многоугольник и найти в нем неизвестные величины.
Графо-аналитический метод целесообразно применять в тех случаях, когда рассматривается равновесие трех сил. При этом по условию задачи в произвольном масштабе строится замкнутый треугольник, который затем решается на основе геометрических либо тригонометрических соотношений.
Метод проекций целесообразно применять для решения задач с числом сил больше трех.
При решении задач на равновесие плоской системы сходящихся сил рекомендуется придерживаться такой общей для всех систем схемы:
- а) выделить тело или точку, равновесие которых рассматривается в данной задаче, и изобразить их на рисунке;
- б) выяснить, какие нагрузки действуют на тело (точку) и также изобразить их на рисунке;
- в) освободить выделенное тело (точку) от связей и заменить их действие реакциями, которые надо изобразить на том же рисунке;
- г) на основе полученной схемы сил построить замкнутый силовой треугольник (если рассматривается равновесие трех сил) или составить уравнения равновесия; причем при составлении уравнений проекций оси целесообразно расположить так, чтобы их направления были параллельны или перпендикулярны к искомым силам (оси проекций также показываются на рисунке);
- д) после решения уравнений равновесия полученные результаты необходимо проверить либо при помощи неиспользованных уравнений или соотношений, либо путем решения задачи другим способом.
Задача №1
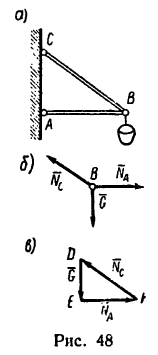
Фонарь весом 9 кГ подвешен на кронштейне АВС (рис. 48, а). Определить реакции горизонтального стержня АВ и наклонной тяги ВС, если АВ 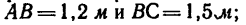
Решение —графо-аналитическим методом с применением геометрических соотношений.
1. В данном случае на шарнир В действуют три силы; вес фонаря G (рис. 48, 6) и реакции стержней 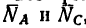
Заметим, что стержень АВ сжат, значит реакция 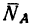
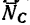
2. Так как шарнир В под действием этих трех сил находится в равновесии, силовой треугольник, составленный из них, должен быть замкнутым.
Выберем произвольную точку D (рис. 48, в) и отложим от нее отрезок DE, изображающий силу G. Из точек Е и D проведем прямые EF и DF, параллельные соответственно АВ и СВ. В полученном треугольнике DEF сторона EF изображает реакцию 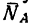
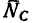
3. Так как в условии задачи даны линейные размеры кронштейна, величины сил 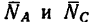
4. Неизвестную в задаче длину АС определяем по теореме Пифагора:
* Если все указанные в п. 2 построения выполнить в определенном масштабе, а затем измеренные длины FF и FD умножить на масштаб построения, то получим решение задачи графическим методом.
5. Окончательно
Задача №2
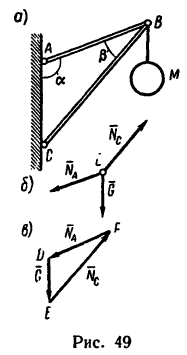
В точке В кронштейна АВС (рис. 49, а) подвешен груз М массой 816 кг. Определить реакции стержней кронштейна, если углы кронштейна 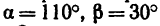
Решение 1— графоаналитическим методом с применением тригонометрических соотношений.
1. На точку В кронштейна действуют три силы: вес груза 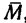
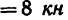
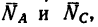
2. Так как эти три силы образуют уравновешенную систему, то составленный из них треугольник должен быть замкнутым (рис. 49, в — построение 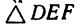
3. 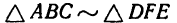
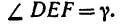
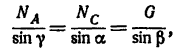
откуда
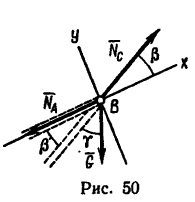
Решение 2—методом проекций при помощи уравнений равновесия.
1. Так как три силы 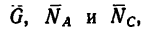
2. Выберем оси координат так, чтобы одна из осей совпадала с линией действия одной из неизвестных сил (см. рис. 50), и составим два уравнения проекций:
Как видно, ответ получается тот же.
После решения задач, аналогичных 39-8 и 40-8, можно сделать ошибочный вывод, что силовой треугольник и треугольник, образованный стержнями кронштейна, должны быть подобными. Но это совсем не обязательно. В этом легко убедиться, рассмотрев следующую задачу.
Задача №3
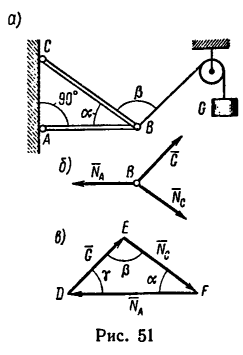
К шарниру В кронштейна АВС прикреплена веревка, перекинутая через блок, к другому концу которой прикреплен груз весом G= 1,5 кн (рис. 51. а).
Определить усилия в стержнях АВ и СВ кронштейна, если крепления в точках А и С шарнирные, а = 35° и 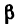
Решение 1-графо-аналитическим методом с применением тригонометрических соотношений.
1. На шарнир В в направлении к блоку действует натяжение веревки, равное весу груза G, и вызывает появление двух усилий, направленных вдоль стержней.
При этом стержень АВ растягивается, а стержень СВ сжимается.
Так как рассматривается равновесие шарнира В, то отбросим стержни, заменив их реакциями 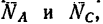
2. Силы G, 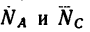
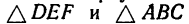
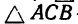
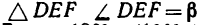
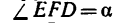
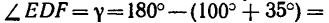
3. Применив к 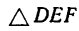
Решение 2—методом проекций.
1. Изобразив шарнир В вместе с действующими на него силами 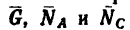
2. Из уравнения (2)
а из уравнения (1)
Как и следовало ожидать, оба решения дают одинаковый результат. Реакции стержней (их действия на шарнирный болт В) равны 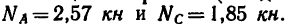
В связи с решением подобных задач методом проекций необходимо отметить следующее. Применяя метод проекций к определению равнодействующей любого числа сходящихся сил, наиболее удобно использовать обычную прямоугольную систему координатных осей. При этом найденные проекции равнодействующей и искомая равнодействующая образуют прямоугольный треугольник, решая который легко определить модуль и направление равнодействующей.
Применяя метод проекций к решению задач на равновесие сил, совсем не обязательно использовать взаимно перпендикулярные оси.
В тех случаях, когда определяются модули сил, направления которых заданы (как в задачах, каждую из осей целесообразно расположить перпендикулярно к направлению искомых сил. Тогда в каждое уравнение равновесия войдет только одно неизвестное.
Решим таким образом ту же задачу 41-8.
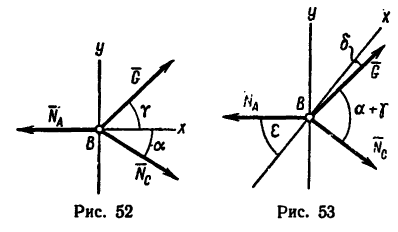
1. Изобразим шарнирный болт В с действующими на него силами (рис. 53).
Расположим ось х перпендикулярно 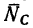
2. Замечая, что 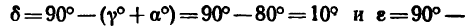
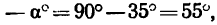
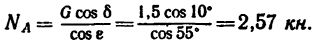
3. Расположим вторую ось (ось у) перпендикулярно к направлению силы 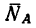
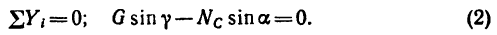
4. Из уравнения (2) 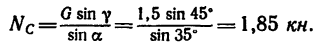
Возможность произвольного расположения осей проекций позволяет производить проверку решения задачи. Чтобы проверить правильность решения задачи, проведенного любым способом, следует выбрать расположение оси таким образом, чтобы на нее спроектировались обе найденные силы. При правильном решении сумма проекций на вновь выбранную ось получится равной нулю. Если же сумма не равна нулю, нужно искать допущенную в решении ошибку.
Задача №4
При помощи стержневого устройства АВС (в точках А, В и С соединения шарнирные) удерживаются в равновесии
два груза — первый весом 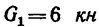
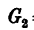
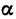
В этой задаче на шарнир В действуют уже не три, а четыре силы, поэтому решать задачу графо-аналитическим методом не имеет смысла — решение получится слишком длинным.
Когда на устройство, состоящее из двух стержней, действует одна нагрузка (как в задачах 38-8, 40-8 и 41-8), то можно легко определить, какой из стержней растянут и какой сжат.
В данной задаче это сразу определить нельзя, так как груз 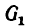
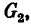
При решении задачи графическим методом направления усилий в стержнях определяют следующим образом.
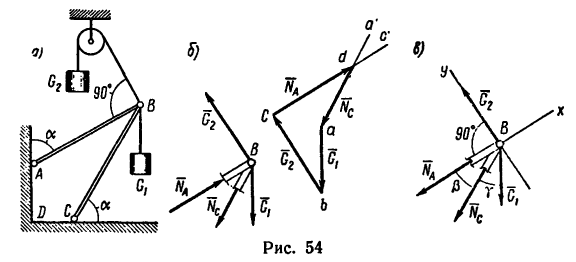
Выбрав масштаб сил, из произвольной точки а построим отрезок ab, изображающий вектор 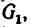
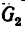
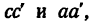
Получается замкнутый силовой четырехугольник abcd (рис. 54, б), в котором стороны cd и da изображают соответственно реакции 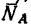
- 1) реакция
действует на шарнир в направлении от стержня к шарниру — значит стержень АВ сжат;
- 2) реакция
действует на шарнир в направлении от шарнира к стержню —значит стержень СВ растянут.
При решении методом проекций нет необходимости заранее определять, в какую сторону направлены реакции вдоль стержней. Целесообразнее предположить, что под действием нагрузки все стержни растянуты (т. е. их реакции направлены от шарнира, равновесие которого рассматриваем, к стержням). Затем выбрать оси проекций, составить уравнения равновесия и решить их. У действительно растянутых стержней модули их реакций получатся положительными (предположительное направление реакций совпадает с действительным), а у сжатых стержней модули их реакций получатся отрицательными (предположительное направление реакций противоположно действительному).
Учитывая изложенное выше, приступим к решению задачи.
1. Изобразим шарнир В с действующими на него нагрузками 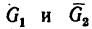
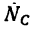
2. Совместим оси проекций с силами 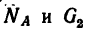
3. Прежде чем приступить к решению уравнений, нужно найти углы
Угол 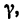
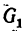
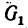
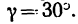
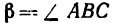
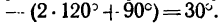
4. Из уравнения (2) 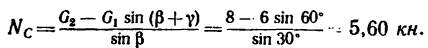
Таким образом, стержень ВС растянут силой 5,60 кн. Из уравнения (1)
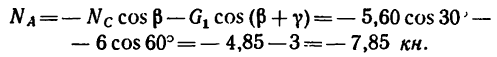
Следовательно, стержень АВ сжат силой 7,85 кн.
Задача №5
Каждую силу Р нужно дополнительно приложить к шарниру В стержневого устройства, описанного в задаче 42-8, чтобы оба стержня АВ и СВ были растянуты усилиями 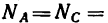
1. Используя рис. 54, айв, изобразим шарнир В с действующими на нем силами 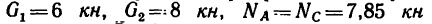
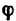
2. Составим уравнения равновесия:
3. В каждое из уравнений входят обе неизвестные величины — модуль силы 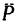
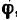
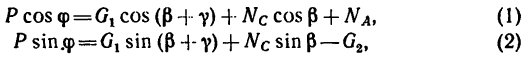
а потом уравнение (2) разделить на уравнение (1):
Отсюда
4. Подставив найденное значение угла 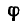
Из уравнения (2)
Так как числитель этого выражения определен в п. 3 и равен 1,12, а знаменатель 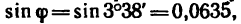
Таким образом, для того чтобы оба стержня были растянуты с одинаковыми усилиями по 7,85 кн, к шарниру В необходимо добавить силу 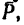
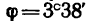
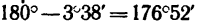
Задачу 43-8 можно было решить по примеру задач, приведенных в § 7-2. Для четырех заданных сил 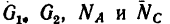
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Равновесие трех непараллельных сил
- Сочлененные системы
- Равновесие пространственной системы сходящихся сил
- Определение положения центра тяжести тела
- Обобщенные координаты системы
- Сложение двух сил
- Разложение силы на две составляющие
- Определение равнодействующей сходящихся сил
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Кинематический анализ и структурный анализ конструкций. Опоры. Связи. Мгновенная изменяемость.Скачать

К шарниру а стержневого шарнирного четырехугольника
Глава 18. Принцип возможных перемещений.
18.3. Принцип возможных перемещений.
18.3.1. Зубчатая передача состоит из двух колес с числом зубьев z2 = 2z1. На колесо 1 действует пара сил с моментом М1 = 10 Н • м. Определить в случае равновесия передачи модуль момента пары сил, действующей на колесо 2. (Ответ 20)
18.3.2. Определить момент М пары сил, который необходимо приложить к барабану 2 радиуса r = 20 см для равномерного подъема груза 1 весом 200Н. (Ответ 20)
18.3.3. Определить усилие в стержне АС плоской фермы, если к узлу В приложена горизонтальная сила F = 6 • 10 3 Н. (Ответ 3 • 10 3 )
18.3.4. Механизм, состоящий из зубчатых колес 1, 2 с числом зубьев z2 = 2z1 и барабана 3, жестко скрепленного с колесом 2, равномерно перемещает груз 4 весом 4 • 10 3 Н. Определить момент М пары сил, если коэффициент трения скольжения груза f = 0,2 и радиус барабана r = 10 см. (Ответ 40)
18.3.5. К зубчатому колесу 1 приложена пара сил с моментом M1 = 40 Н • м. Определить момент М пары сил, который необходимо приложить к кривошипу ОА, для того чтобы механизм находился в равновесии, если радиусы r1 = r2. (Ответ 80)
18.3.6. На тело 3 действует сила F = 460Н параллельно его плоскости опоры. Определить модуль силы давления тела 2 на сжимаемое тело 1 при равновесии системы. (Ответ 920)
18.3.7. На клин 3 действует сила F = 100Н. Определить с какой силой толкатель 2 прижимает деталь 1 к опорной плоскости в положении равновесия, если угол α = 11°. (Ответ 514)
18.3.8. Передаточное отношение червячной передачи лебедки равно 50. Определить модуль силы F, которую необходимо приложить к рукоятке длиной l = 0,2 м для равномерного подъема груза 1 весом 4 • 10 3 Н. Радиус барабана r = 0,12 м. (Ответ 48)
18.3.9. К шатуну АВ шарнирного параллелограмма ОАВС приложена горизонтальная сила F = 50Н. Определить модуль момента М пары сил, которую необходимо приложить к кривошипу ОА длиной 10 см, для того чтобы уравновесить механизм. (Ответ 4,33)
18.3.10. На первую часть трехшарнирной арки действует вертикальная сила F = 8 • 10Н Определить модуль вертикальной составляющей реакции шарнира А. (Ответ 2 • 10 3 )
18.3.11. Определить модуль уравновешивающей силы F, приложенной к кривошипу ОА в точке А шарнирного четырехзвенника ОABC, если на шатун АВ = 0,4 м действует пара сил с моментом М = 40 Н • м. (Ответ 100)
18.3.12. Определить модуль силы F2, которую необходимо приложить к ползуну, для того чтобы механизм находился в равновесии, если сила F1 = 100Н и длина ОА = АВ. (Ответ 200)
18.3.13. Определить модуль силы F1, которую необходимо приложить к кривошипу AB, для того чтобы механизм находился в равновесии, если сила F2 = 100Н и расстояние ОА = 2 ОВ.
(Ответ 100)
18.3.14. Горизонтальная балка АС заделана концом С в вертикальную стену и нагружена парой сил с моментом М2 = 600 Н • м. Балка АВ, опирающаяся на подвижную опору своим концом В, нагружена парой сил с моментом М1 = 400 Н • м. Определить модуль момента заделки.
(Ответ 400)
18.3.15. Балки АС и CD соединены между собой шарниром С. Горизонтальная балка АС опирающаяся на ребро В призмы, нагружена парой сил с моментом М = 2 • 10 3 Н • м. Балка CD нагружена посередине силой F = 4 • 10 3 Н. Определить модуль реакции опоры В.
(Ответ 8,93 • 10 3 )
18.3.16. Найти модуль уравновешивающей силы F, если к стержню 1 стержневого механизма приложена сила F1 = 400Н. (Ответ 346)
18.3.17. Стержни АВ и CD, соединенные между собой и с неподвижным основанием шарнирами, нагружены силами F1 = 200Н и F2 = 600Н. Определить модуль горизонтальной составляющей реакции шарнира А, если длины AE = BE = BC= BD = 1м. (Ответ 500)
18.3.18. С помощью гидроцилиндра 1 удерживается в равновесии стрела 2, на конце которой приложена вертикальная сила F = 400Н. Определить в кН силу давления масла на поршень гидроцилиндра, если длина АВ = ВС. (Ответ 0,924)
18.3.19. На стержень 2 механизма действует горизонтальная сила F = 3 кН. Определить в кН силу давления масла на поршень гидроцилиндра 1 в положении равновесия системы. (Ответ 6)
18.3.20. На поршень 1 действует сила F = 250Н. Определить, с какой силой рычаг ABC прижимает деталь 2 к основанию 3 в положении равновесия системы, если угол α = 30° и расстояния АВ = 0,8 м, ВС = 0,4 м. (Ответ 866)
18.3.21. На шатун АВ шарнирного параллелограмма ОАВС надета втулка 2, к которой с помощью шарнира D прикреплен вертикальный стержень 3. Определить в случае равновесия механизма момент М пары сил, если сила F = 400Н и длина кривошипа ОА = 0,2 м. (Ответ 40)
18.3.22. Определить момент М пары сил, который необходимо приложить к валу зубчатого колеса 3 для равномерного подъема груза 1 весом 900Н. Радиус барабана r = 0,2 м, числа зубьев колес z2 = 2z3. (Ответ 90)
18.3.23. Определить модуль момента М нары сил, который необходимо приложить к шкиву 3 для равномерного подъема груза 1 весом 900Н. Радиусы шкивов R = 2r = 40 см. (Ответ 90)
18.3.24. Стержень АВ нагружен силой F1 = 800Н и парой сил с моментом М = 70 Н • м. На точку С стержня BCD действует сила F2 = 280Н. Определить модуль горизонтальной составляющей реакции опоры D. (Ответ 202)
18.3.25. На винт 2 с шагом h = 1 см действует пара сил с моментом М = 1 Н • м. Определить силу давления на сжимаемый предмет 1 в положении равновесия механизма пресса, при котором угол α = 45°. (Ответ 628)
🎥 Видео
Кинематический анализ и структурный анализ плоских и пространственных систем. Практика.Скачать

Расчет статически неопределимой стержневой системы. Уравнение совместимости деформацийСкачать

Основы Сопромата. Задача 2. Перемещение шарнирно-стержневой системыСкачать

Фильм № 4. Расчет шарнирно-стержневой системыСкачать
определение реакций в стержнях от действия грузовСкачать

Шарнирные механизмы | Лекции по математике – математик Николай Андреев | НаучпопСкачать

Определение реакций опор простой рамыСкачать

LIRA Sapr Урок №5 Связи и шарнирыСкачать

Задача о составной конструкцииСкачать

Термех. Статика. Расчётно-графическая работа по статике №2. Задание 1 и решениеСкачать

Кинематический анализ 2Скачать
Определение реакций опор составной конструкцииСкачать

Object Creator от Академии Инженерного Искусства. Плагины SCAD++. Соединения. ШарнирыСкачать

Основная система метода перемещенийСкачать

Статически определимые шарнирно-стержневые системы. Построение схем деформаций.Скачать

Основы Сопромата. Виды опор. Определение реакций опорСкачать

План скоростей шарнирного трехзвенного механизмаСкачать

Шарнир: Как работать с шарнирно неподвижной опорой в ЕГЭ по физике 2023.Скачать

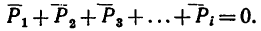
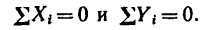
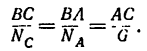
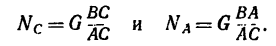
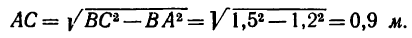
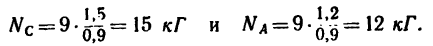

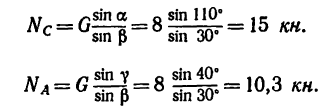
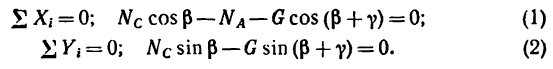
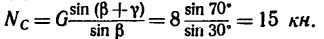
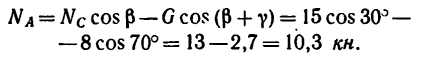
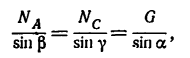
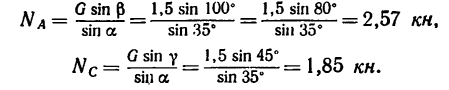
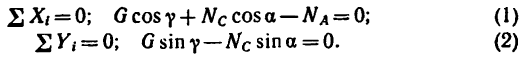
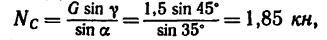
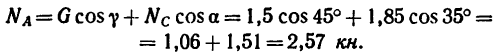
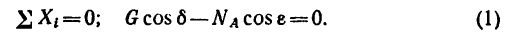
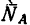 действует на шарнир в направлении от стержня к шарниру — значит стержень АВ сжат;
действует на шарнир в направлении от стержня к шарниру — значит стержень АВ сжат; действует на шарнир в направлении от шарнира к стержню —значит стержень СВ растянут.
действует на шарнир в направлении от шарнира к стержню —значит стержень СВ растянут.