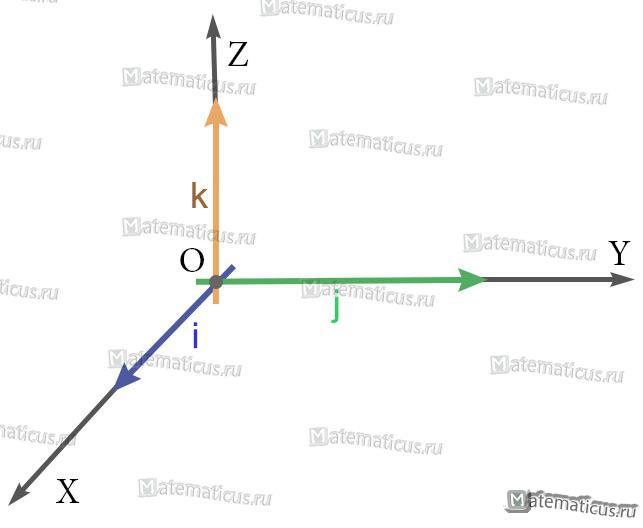
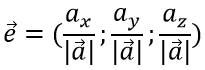Единичный вектор как его найти

Единичный вектор (орты координатных осей) — это вектор, длина которого равна единице.

i — единичный вектор оси абсцисс;

j — единичный вектор оси ординат;

k — единичный вектор оси аппликат.

i⊥j⊥k, i=j=k=1

В прямоугольной системе координат в пространстве координаты векторов равны:

i(1;0;0), j(0;1;0), k(0;0;1)

Единичные векторы являются некомпланарными.

Любой вектор можно разложить в виде вектора по ортам координатных осей, формула ниже.

a=xi+уj+zk

где x, y, z — координаты вектора проекции на соответствующие координатные оси.

Эта формула называется разложением вектора по ортам координатных осей.

Единичный вектор определяется по формуле:

Дан вектор а = (1; 2; -2)

Требуется найти длину (модуль) и единичный вектор e направления вектора а

Находим длину вектора a

затем вычисляем единичный вектор e

Видео:Координаты вектора. 9 класс.Скачать

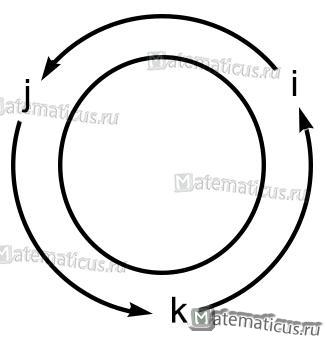
Векторное произведения единичных векторов

Если направление кратчайшего пути от первого вектора ко второму вектору совпадает с направлением стрелки, то произведение равно третьему вектору, а если не совпадает, то третий вектор берется со знаком «минус» . Смотрите схему 1.

На основании схемы получаем таблицу векторного произведения единичных векторов

Пример 1
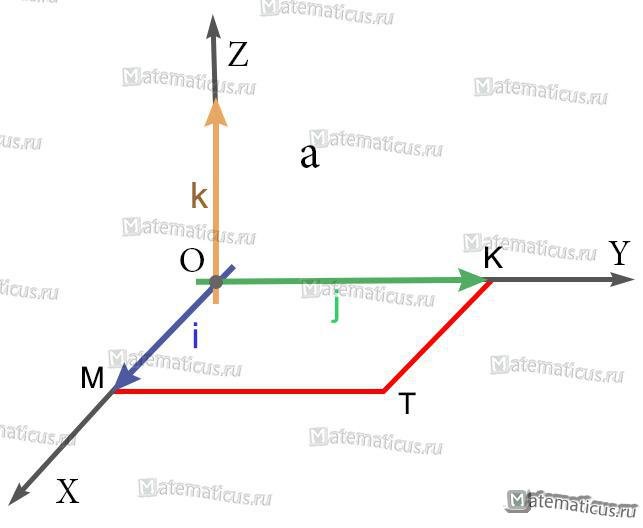
Найти векторное произведение iхj, где i, j — единичные векторы (орты) правой системы координат.

Решение
1) Так как длины основных векторов равны единице масштаба, то площадь параллелограмма MOKT численно равна единице. Значит, модуль векторного произведения равен единице.
2) Так как перпендикуляр к плоскости MOKT есть ось OZ, то искомое векторное произведение есть вектор, коллинеарный с вектором k; а так как оба они имеют модуль 1, то искомое векторное произведение равно либо k, либо -k.
3) Из этих двух возможных векторов надо выбрать первый, так как векторы i, j, k образуют правую систему (а векторы i, j, -k — левую).

iхj=k

Пример 2
Найти векторное произведение jхi.

Решение
Как в примере 1, заключаем, что вектор jхi равен либо k, либо —k. Но теперь надо выбрать -k, ибо векторы j, i, —k образуют правую систему (а векторы i, j, —k -левую).
jхi = −k

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 3.5 / 5. Количество оценок: 4

Видео:Орт вектора. Нормировать вектор. Найти единичный векторСкачать

Вектор: определение и основные понятия

Видео:Единичный векторСкачать

Определение вектора

рис. 1

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Обозначение вектора

Вектор началом которого есть точка А, а концом — точка В, обозначается AB (рис.1). Также вектора обозначают одной маленькой буквой, например a .

Видео:Разложение вектора по базису. 9 класс.Скачать

Длина вектора

Для обозначения длины вектора используются две вертикальные линии слева и справа | AB |.

Видео:Как выражать вектор? Как решать задачу с вектором? | TutorOnlineСкачать

Нулевой вектор

Нулевой вектор обычно обозначается как 0 .

Длина нулевого вектора равна нулю.

Видео:Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Коллинеарные вектора

рис. 2

Видео:найти угол между единичными векторамиСкачать

Сонаправленные вектора

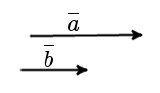рис. 3

Видео:Единичные векторы и инженерная запись (видео 34) | Криволинейное движение | ФизикаСкачать

Противоположно направленные вектора

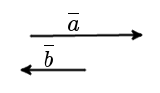рис. 4

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Компланарные вектора

рис. 5

Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.

Видео:Найдите разложение вектора по векторам (базису)Скачать

Равные вектора

рис. 6

То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:

a = b , если a ↑↑ b и | a | = | b |.

Видео:Единичные векторы Декартовой системы координатСкачать

Единичный вектор

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:1. Векторы и параллелограмм задачи №1Скачать

Единичные векторы: характеристики, как получить, примеры

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Содержание:

В единичные векторы — это те, модуль, величина или размер которых равны числовому значению. Единичные векторы полезны для указания направления других неединичных векторов.

Помните, что векторы — это математические объекты, которые математически представляют физические величины, зависящие от направления, такие как сила, скорость, ускорение и другие.

Независимо от физической величины, с которой они связаны, единичные векторы лишены единиц измерения, и их размер всегда равен 1, чистому числу.

Например, скорость частицы, движущейся со скоростью 3 м / с в положительном направлении декартовой оси X, обозначается: v = (3 м / с) я, где жирным шрифтом обозначены векторные величины. В этом примере модуль v составляет 3 м / с, а модуль единичного вектора я равно 1 (без единиц).

Видео:#вектор Разложение вектора по ортам. Направляющие косинусыСкачать

Модуль, направление и смысл

Учитывая, насколько важно установить ориентацию этих величин для того, чтобы узнать их влияние, векторы имеют три важные характеристики: величину или модуль, связанный с размером вектора, направление и смысл. При представлении векторной величины необходимо четко указать эти аспекты.

Теперь единичный вектор может иметь любое направление и любое значение, но величина всегда должна быть равна 1.

Единичные векторы используются для обозначения конкретного направления в пространстве или на плоскости. Если, например, нам нужно работать со всеми силами, которые действуют вдоль горизонтальной оси, то единичный вектор в этом направлении помогает нам отличать эти силы от других, направленных в другом направлении.

А чтобы отличить их от неединичных векторов, в печатных буквах обычно используется жирный шрифт, а сверху ставится каретка, например:

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Характеристики единичного вектора

Математически единичный вектор:

Итак, мы можем установить, что:

-Модуль единичного вектора всегда равен 1, не имеет значения, является ли это силой, скоростью или другим вектором.

-Унитарные векторы имеют определенное направление, а также смысл, например единичный вектор в вертикальном направлении, который может иметь смысл вверх или вниз.

-Единичные векторы имеют точку происхождения. Когда она представлена ​​декартовой системой координат, эта точка совпадает с началом системы: (0,0), если это плоскость, или (0,0,0), если вектор находится в трехмерном пространстве.

-Также с единичными векторами вы можете выполнять все операции сложения, вычитания и умножения векторов, которые выполняются с использованием обычных векторов. Следовательно, можно умножать единичный вектор на скаляр, а также выполнять точечное произведение и кросс-произведение.

-С помощью единичного вектора в определенном направлении могут быть выражены другие векторы, которые также ориентированы в этом направлении.

Видео:СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Единичные векторы в пространстве

Чтобы выразить любой вектор в пространстве или на плоскости, можно использовать набор единичных векторов, перпендикулярных друг другу, которые образуют ортонормированный базис. Каждое из трех предпочтительных направлений пространства имеет собственный единичный вектор.

Вернемся к примеру сил, направленных по горизонтальной оси. Это ось абсцисс, которая имеет две возможности: вправо и влево. Предположим, у нас есть единичный вектор на оси x, направленный вправо, который мы можем обозначить любым из следующих способов:

Любой из них действителен. Теперь предположим, что сила F₁ величиной 5 Н вдоль этой оси и направленной вправо такую ​​силу можно выразить как:

Если бы сила была направлена ​​вдоль оси x, но в противоположном направлении, то есть влево, то для установления этой разницы можно было бы использовать отрицательный знак.

Например, сила величиной 8 Н, расположенная по оси x и направленная влево, будет выглядеть так:

А для векторов, которые не направлены вдоль декартовых осей, также есть способ представить их в терминах ортогональных единичных векторов, используя их декартовы компоненты.

Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

Как получить / рассчитать единичный вектор?

Чтобы вычислить единичный вектор в направлении любого произвольного вектора v, применяется следующая формула:

Это модуль или величина вектора v, квадрат которого рассчитывается так:

Видео:2 37 Нахождение орта вектораСкачать

Произвольный вектор через единичный вектор

В качестве альтернативы вектор v можно выразить так:

То есть произведение его модуля и соответствующего единичного вектора. Именно это и было сделано ранее, когда говорилось о силе величиной 5 Н, направленной вдоль положительной оси x.

Видео:9 класс, 2 урок, Координаты вектораСкачать

Графическое представление

Графически это видно на этом изображении, где вектор v он синего цвета, а соответствующий единичный вектор в его направлении — красным.

В этом примере вектор v его величина больше, чем у единичного вектора, но объяснение справедливо, даже если это не так. Другими словами, у нас могут быть векторы, которые, например, в 0,25 раза больше единичного вектора.

Примеры единичных векторов

Перпендикулярные единичные векторы i, j и k

Как мы видели ранее, перпендикулярные единичные векторы я, j Y k они очень полезны для представления любого другого вектора на плоскости или в пространстве, а также для выполнения векторных операций. В терминах этих векторов произвольный вектор v представлен как:

v = v_Икся + v_Yj + v_zk

Где V_Икс, v_Y и V_z — прямоугольные компоненты вектора v, которые являются скалярами — жирным шрифтом они не выделяются в печатном тексте.

Закон Кулона

Единичные векторы часто появляются в физике. Вот, например, закон Кулона, который количественно описывает взаимодействие двух точечных электрических зарядов.

В нем говорится, что сила F Притяжение или отталкивание между указанными зарядами пропорционально их произведению, обратно пропорционально квадрату расстояния, которое их разделяет, и направлено в направлении единичного вектора, соединяющего заряды.

Этот вектор обычно представлен:

А закон Кулона в векторной форме выглядит так:

Упражнение решено

Найдите единичный вектор в направлении вектора v = 5я + 4j -8kв условных единицах.

Решение

Применяется определение единичного вектора, данное выше:

Но сначала мы должны вычислить модуль вектора, который, поскольку он состоит из трех компонентов, определяется:

|v| 2 = (5) 2 + (4) 2 + (-8) 2 = 25 + 16 + 64 = 105

Поэтому модуль v это:

Искать единичный вектор просто:

Что в конечном итоге приводит нас к следующему:

v = 0.488 я + 0.390 j – 0.781 k

Ссылки

1. Бауэр, В. 2011. Физика для инженерии и науки. Том 1. Мак Гроу Хилл.
2. Бедфорд, 2000. А. Инженерная механика: Статика. Эддисон Уэсли.
3. Фигероа, Д. (2005). Серия: Физика для науки и техники. Том 1. Кинематика. Отредактировал Дуглас Фигероа (USB).
4. Джамбаттиста, А. 2010. Физика. 2-й. Эд. Макгроу Хилл.
5. Резник, Р. (1999). Физический. Том 1. 3-е изд. На испанском языке. Compañía Editor Continental S.A. de C.V.

Кинезический язык: понятие, характеристики, типы, примеры