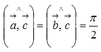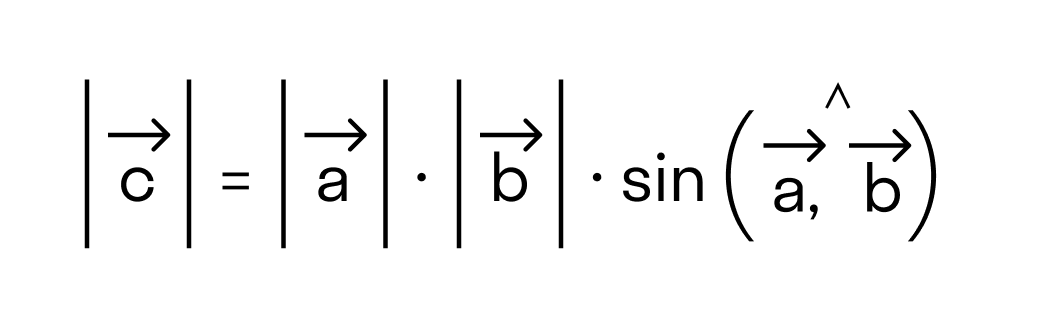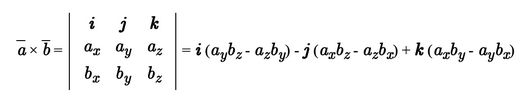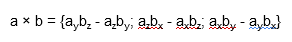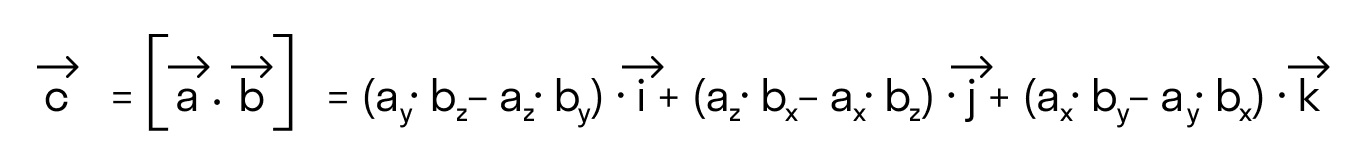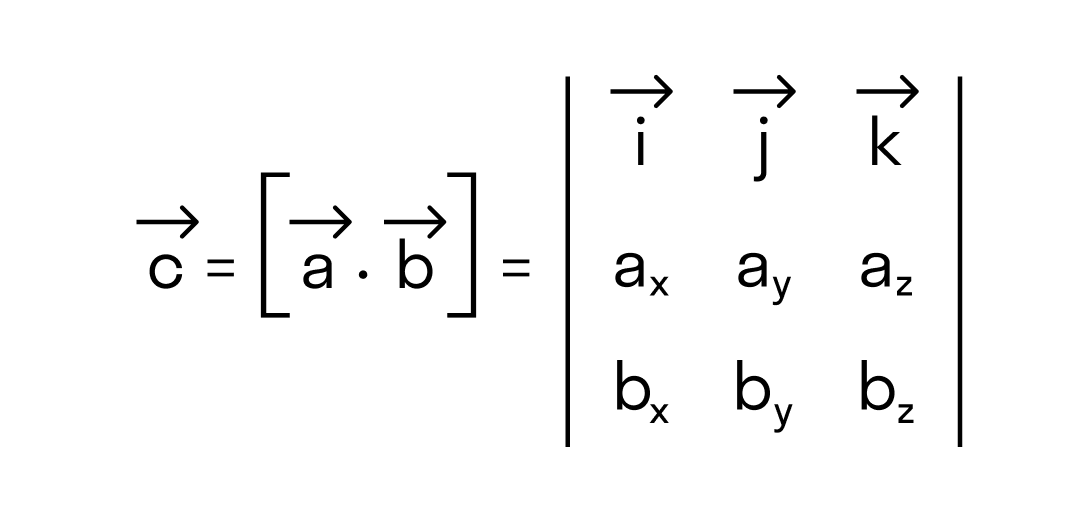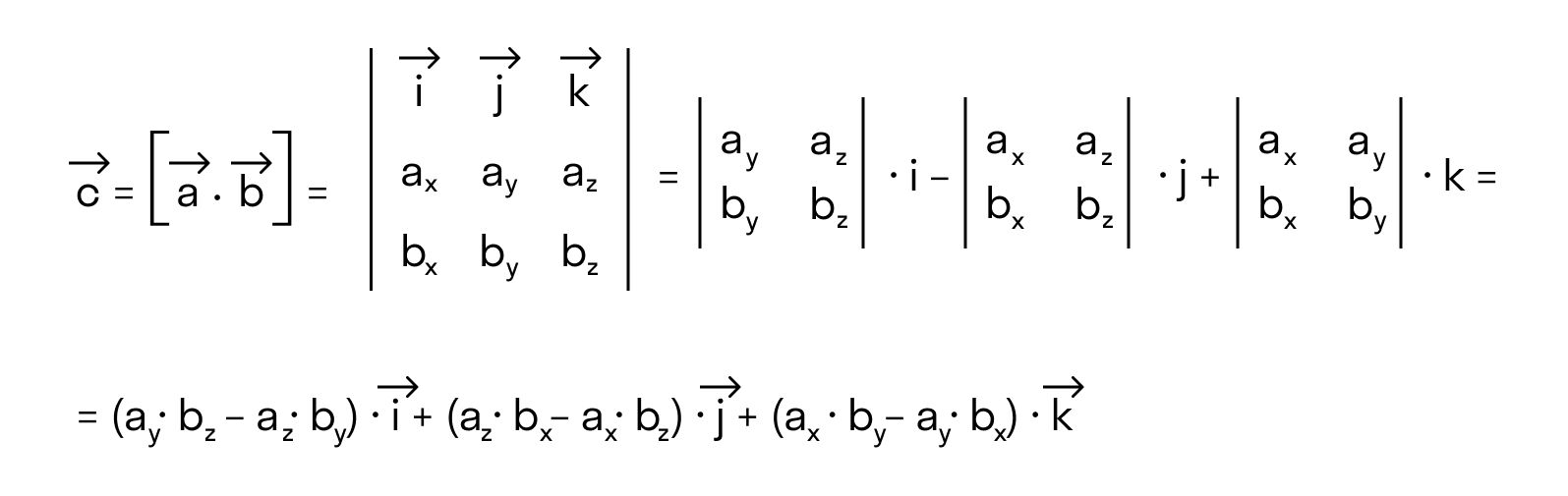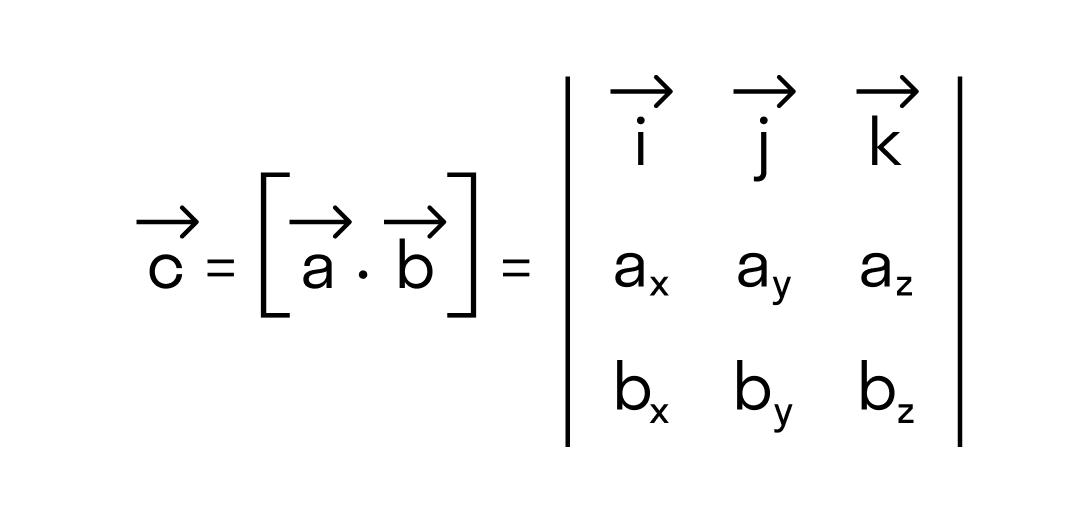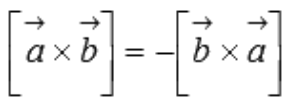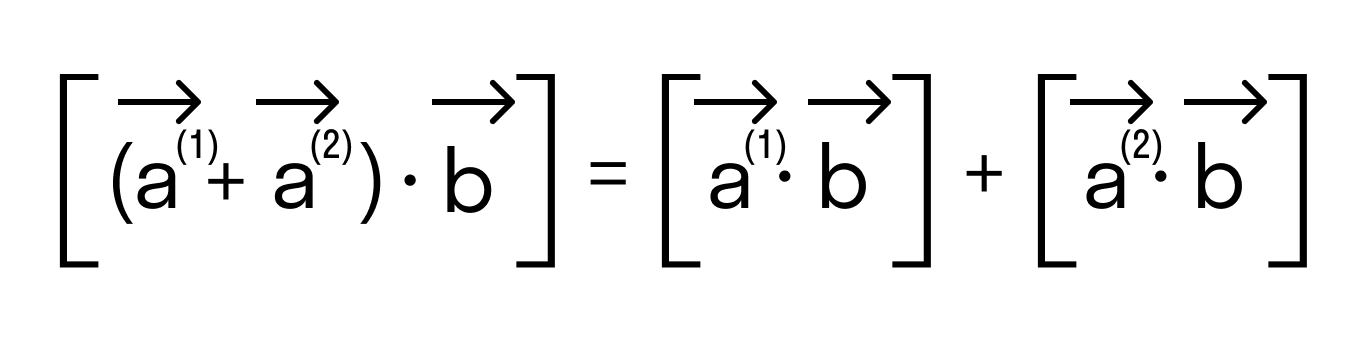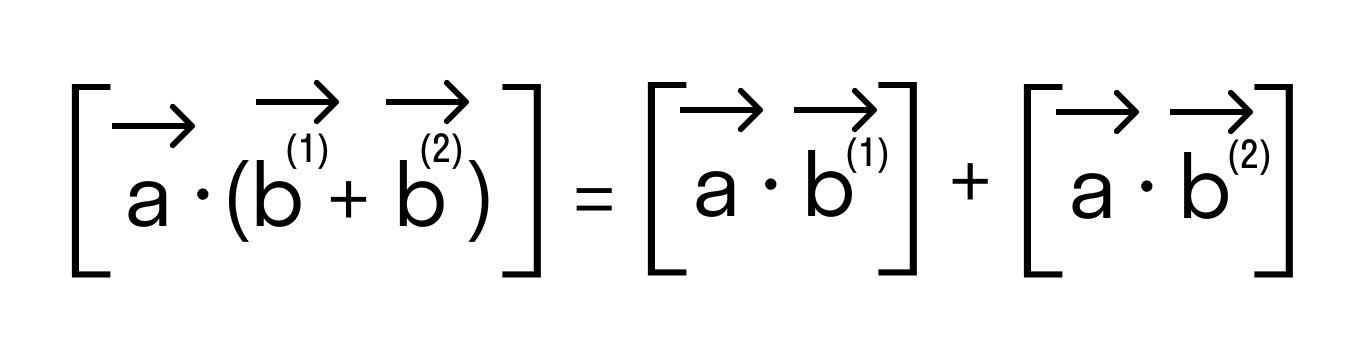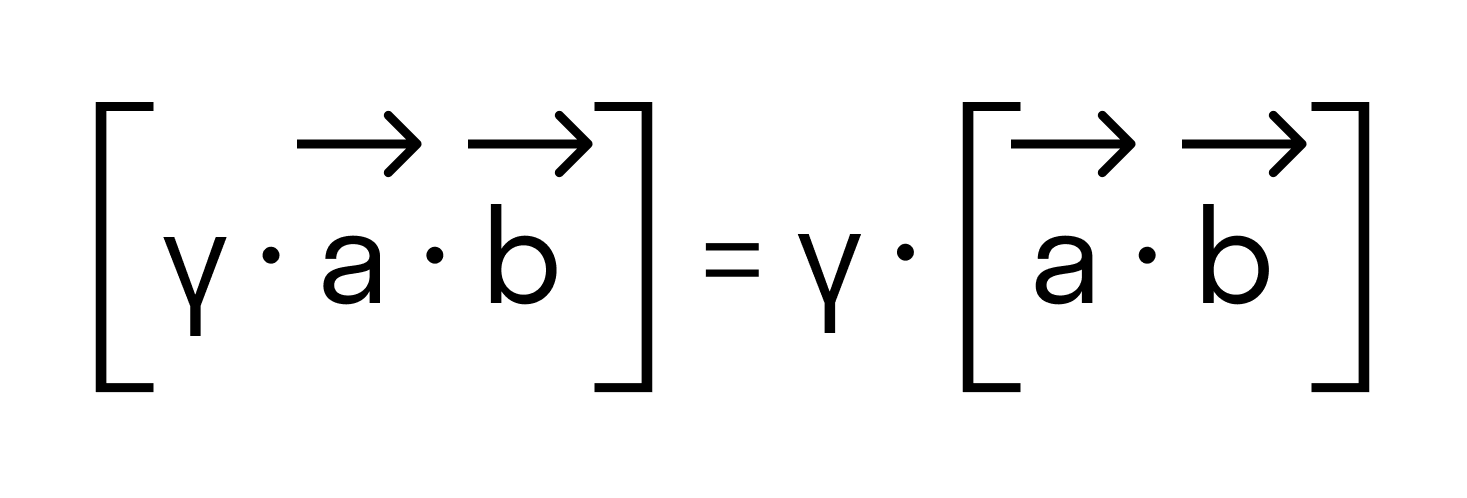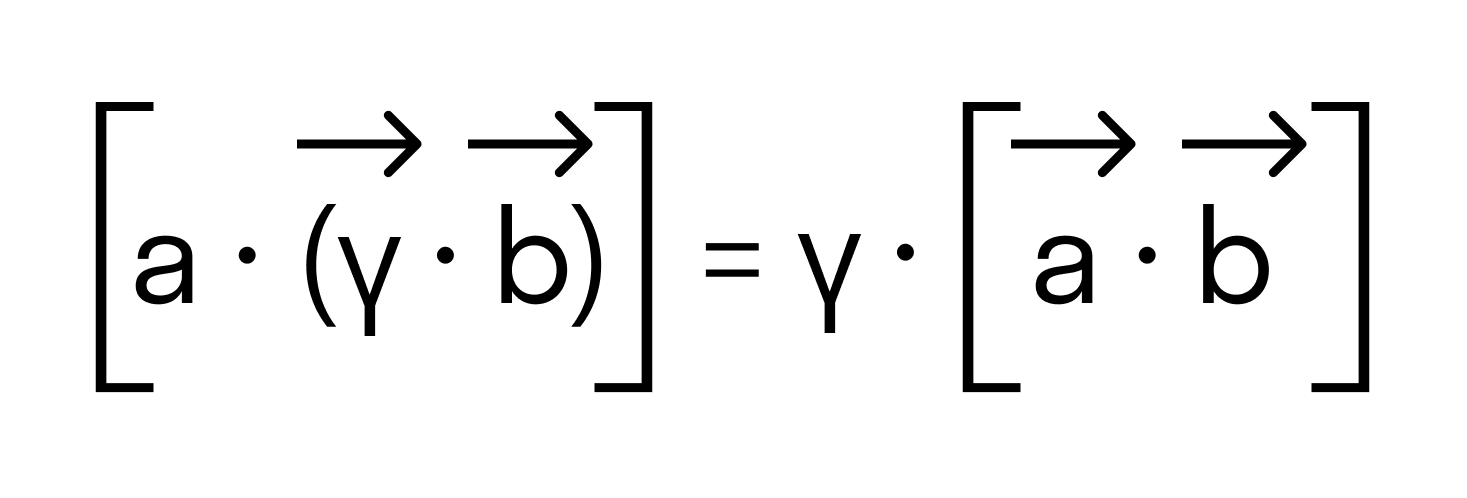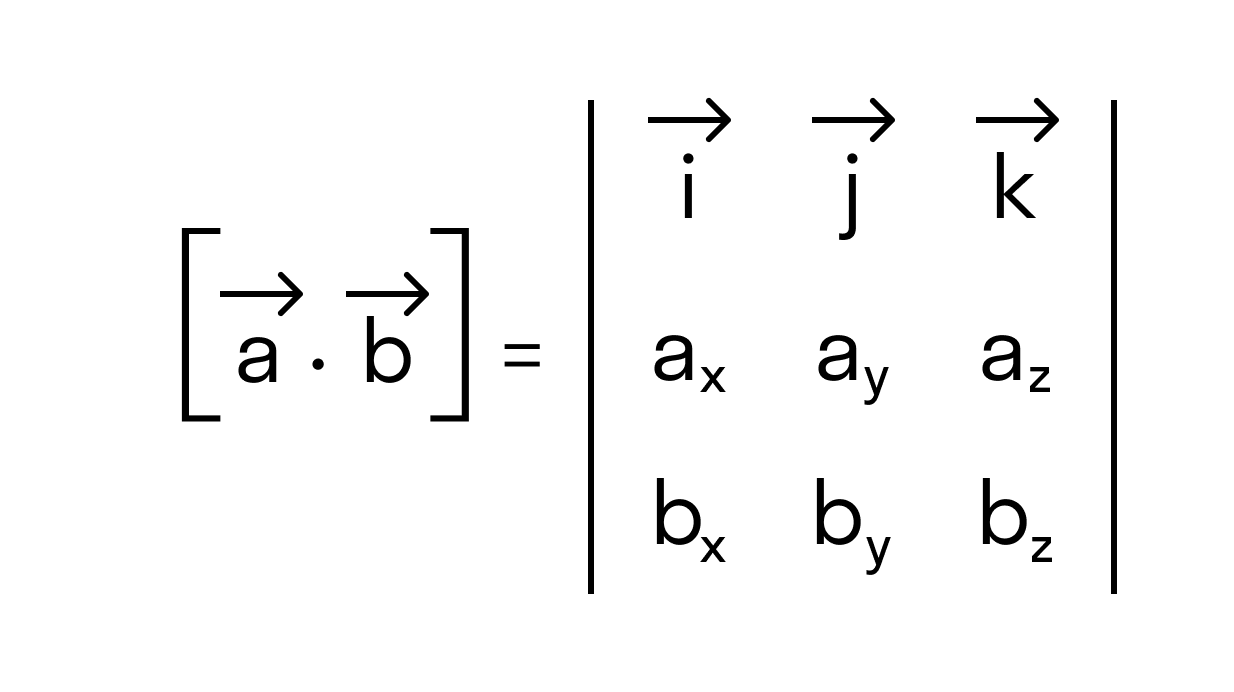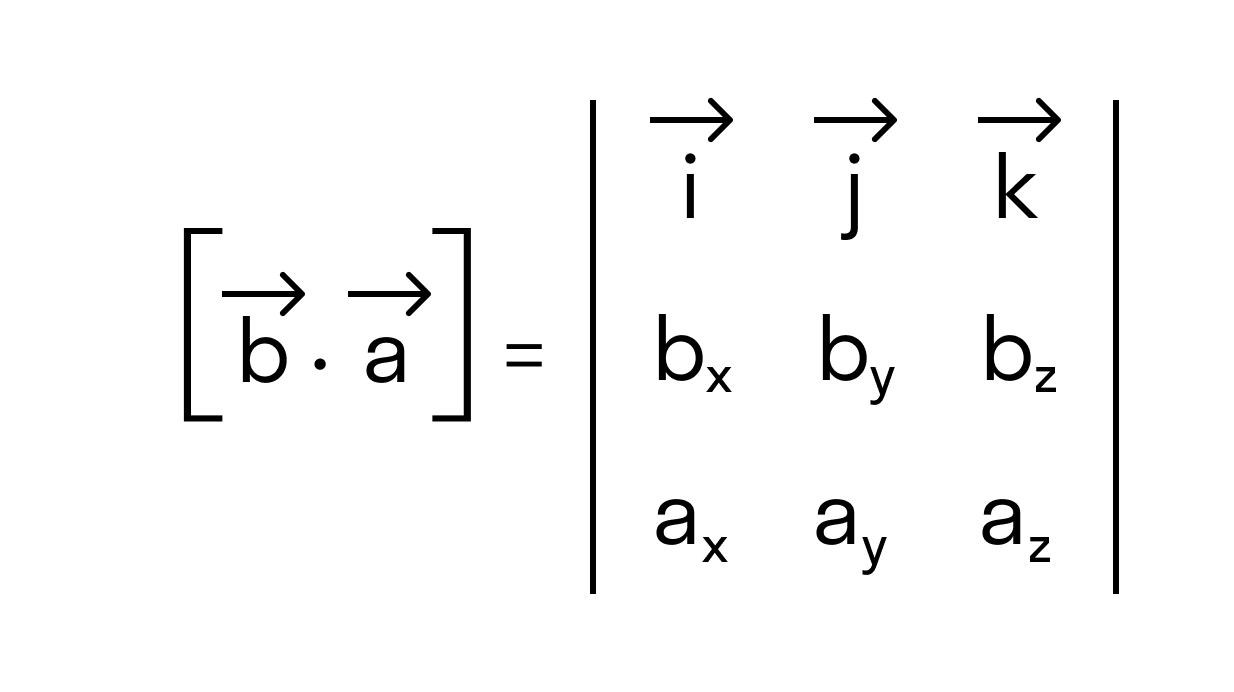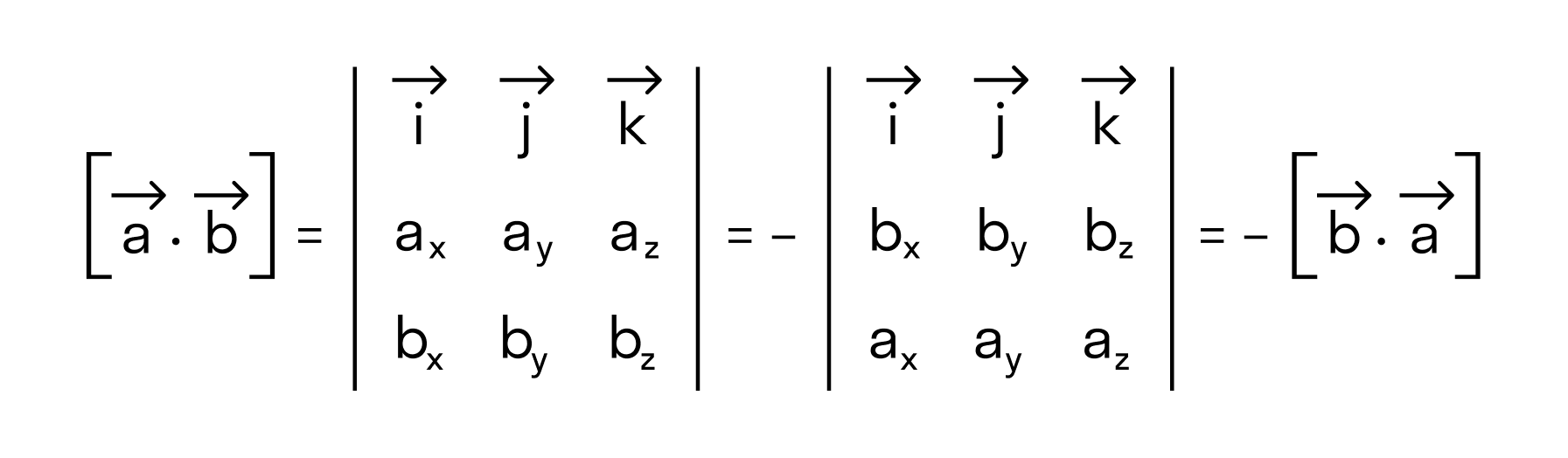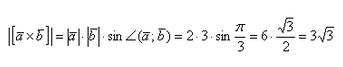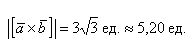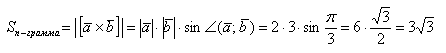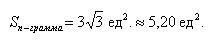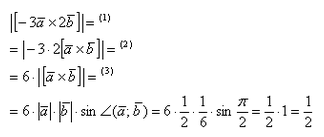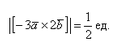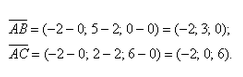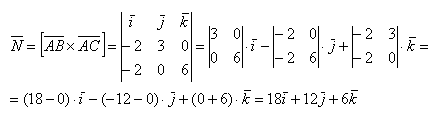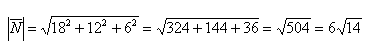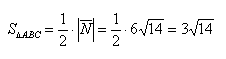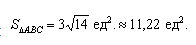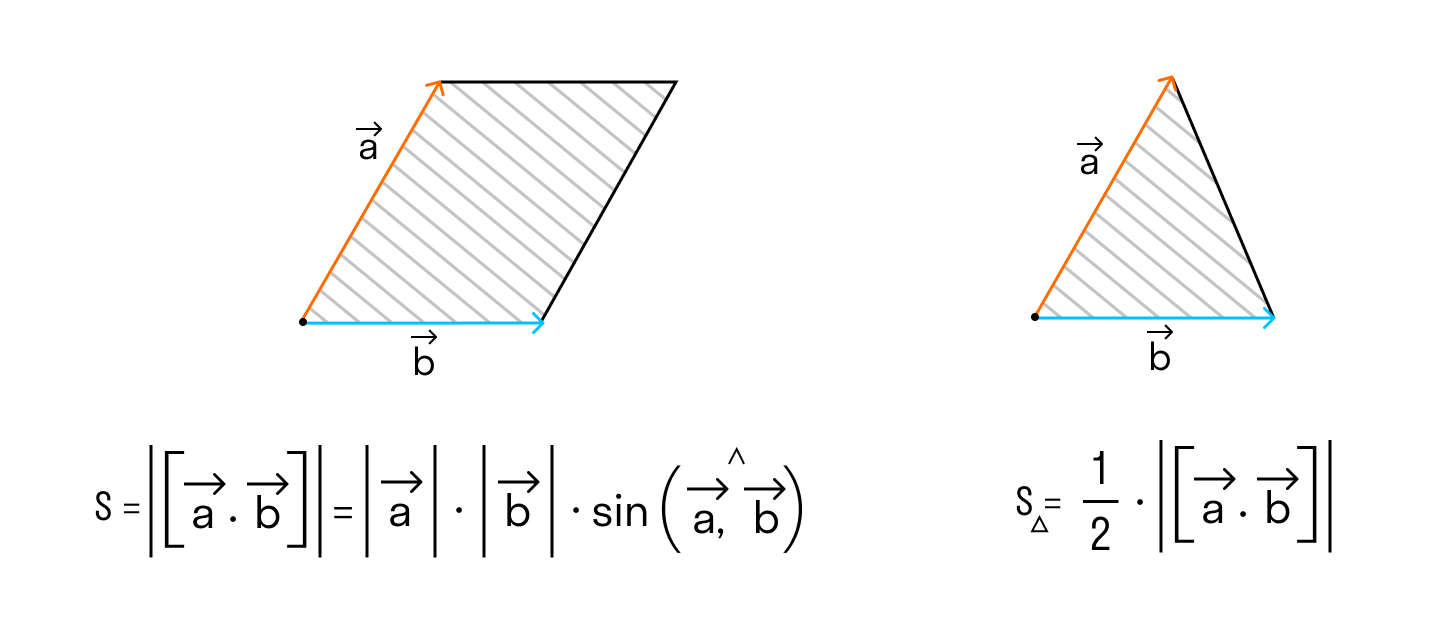 |
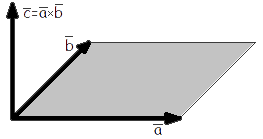
| рис. 1 |
- Формулы вычисления векторного произведения векторов
- Свойства векторного произведения векторов
- Примеры задач на вычисления векторного произведения векторов
- Построить векторы а 3k 2j b 3i 2j
- Векторное произведение векторов
- Определение векторного произведения
- Координаты векторного произведения
- Свойства векторного произведения
- Примеры решения задач
- Пример 1
- Пример 2
- Пример 3
- Геометрический смысл векторного произведения
- Физический смысл векторного произведения
Формулы вычисления векторного произведения векторов
Векторное произведение двух векторов a = < ax ; ay ; az > и b = < bx ; by ; bz > в декартовой системе координат — это вектор, значение которого можно вычислить, используя следующие формулы:
Свойства векторного произведения векторов
| SΔ = | 1 | | a × b | |
| 2 |
Примеры задач на вычисления векторного произведения векторов
| a × b = | i | j | k | = |
| 1 | 2 | 3 | ||
| 2 | 1 | -2 |
= i (2 · (-2) — 3 · 1) — j (1 · (-2) — 2 · 3) + k (1 · 1 — 2 · 2) =
Решение: Найдем векторное произведение этих векторов:
| a × b = | i | j | k | = |
| -1 | 2 | -2 | ||
| 2 | 1 | -1 |
= i (2 · (-1) — (-2) · 1) — j ((-1) · (-1) — (-2) · 2) + k ((-1) · 1 — 2 · 2) =
Из свойств векторного произведения:
SΔ = 1 2 | a × b | = 1 2 √ 0 2 + 5 2 + 5 2 = 1 2 √ 25 + 25 = 1 2 √ 50 = 5√ 2 2 = 2.5√ 2
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Построить векторы а 3k 2j b 3i 2j
12. Даны векторы a = i — 3j + 5k, b = 2i + j + 4k, с = j — k. Найти вектор . если .
13. Найти площадь параллелограмма, построенного на векторах: а) p = 4i + 4j, с = —2i + j; б) p = 3i — 2j + k, с = 3i + 5j + 2k.
14. Найти длину медианы AM и высоты AD в треугольнике ABC, если известно, что AB = 5i + 2j , BC = 2i — 4j.
15. Найти длину высоты CD в треугольнике, вершины которого находятся в точках A(2, 7), B(5, 3), C(6, 8).
16. Найти смешанное произведение векторов a = (7, 0, 1), b = (—2, 4, 4), с = (1, 5, 1).
17. Будут ли компланарны векторы .
18. Вычислить объём пирамиды, вершины которой находятся в точках A(1, 1, 1), B(4, 2, —1), C(—3, 1, 4), D(2, 6, 0).
19. Найти высоту AK треугольной пирамиды, вершины которой находятся в точках A(4, —2, 7), B(1, —1, 6), C(7, 7, 1), D(3, 0, 4).
4.8. Образец теста (для дистанционной формы обучения)
1. Какому условию должны удовлетворять векторы a, b, чтобы .
Указать номер правильного ответа: 1) |a| = |b|; 2) a, b перпендикулярны; 3) a || b; 4) только если a, b нулевые.
2. Найти cos α + cos γ, где α и γ — углы, образованные вектором 8i + 4с + k с осями OX, OZ.
3. Найти скалярное произведение векторов a + b и 2a, если . угол между векторами a, b равен π/3.
4. Найти проекцию на ось OY вектора AB, если его начало и конец находятся в точках A(4, —2 ,1), B(7 ,1, 3).
5. Найти площадь параллелограмма, построенного на векторах .
Векторное произведение векторов
О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Определение векторного произведения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
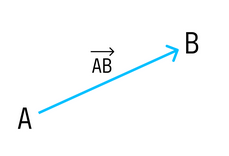
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.
Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.
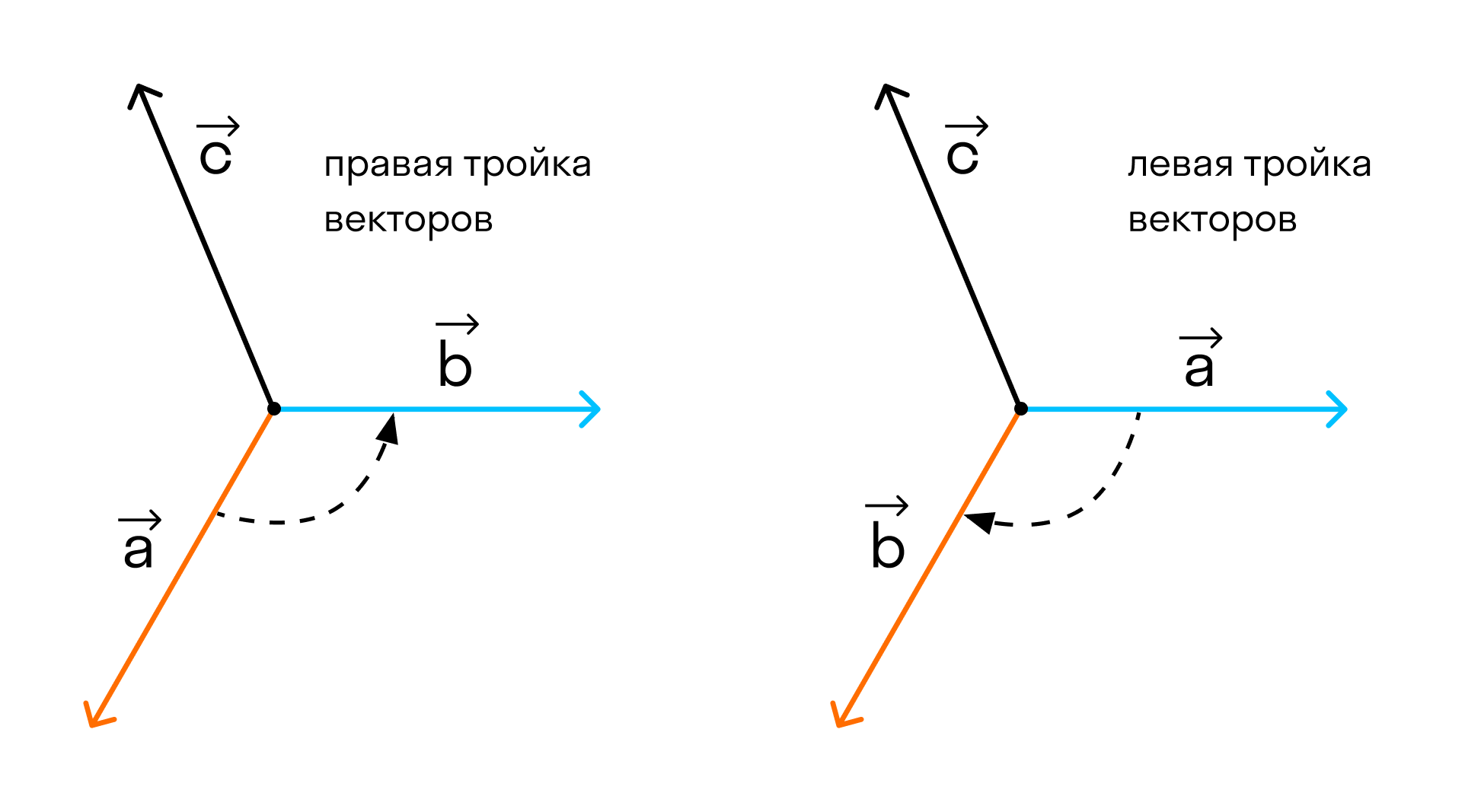
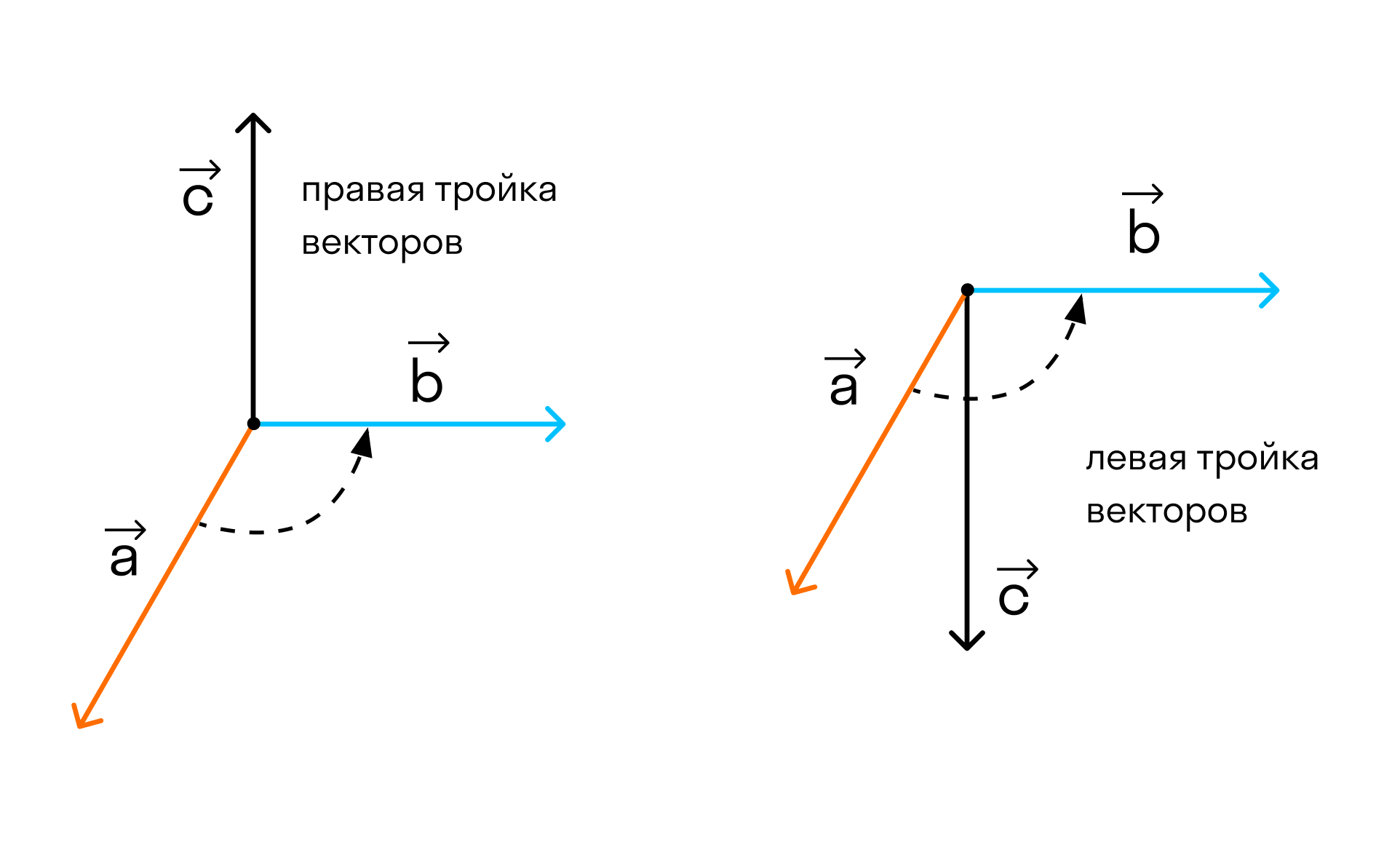
Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.
Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.
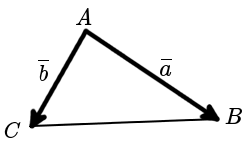
Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.
Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.
В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.
И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.
Еще не устали от теории? Онлайн-школа Skysmart предлагает обучение на курсах по математике — много практики и поддержка внимательных преподавателей!
Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:
- он является нулевым, если векторы →a и →b коллинеарны;
- он перпендикулярен и вектору →a и вектору →b;
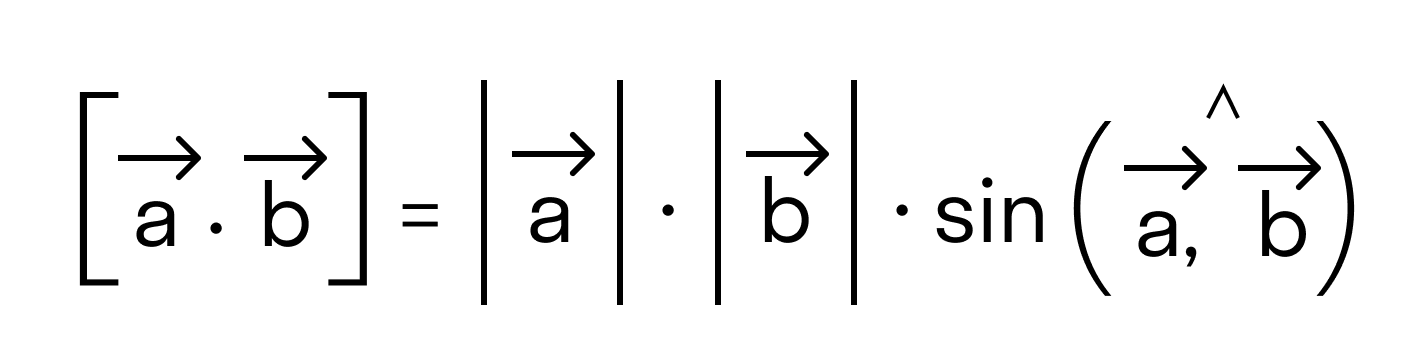
- длина векторного произведения равна произведению длин векторов →a и →b на синус угла между ними
- тройка векторов →a, →b, →c ориентирована так же, как и заданная система координат.
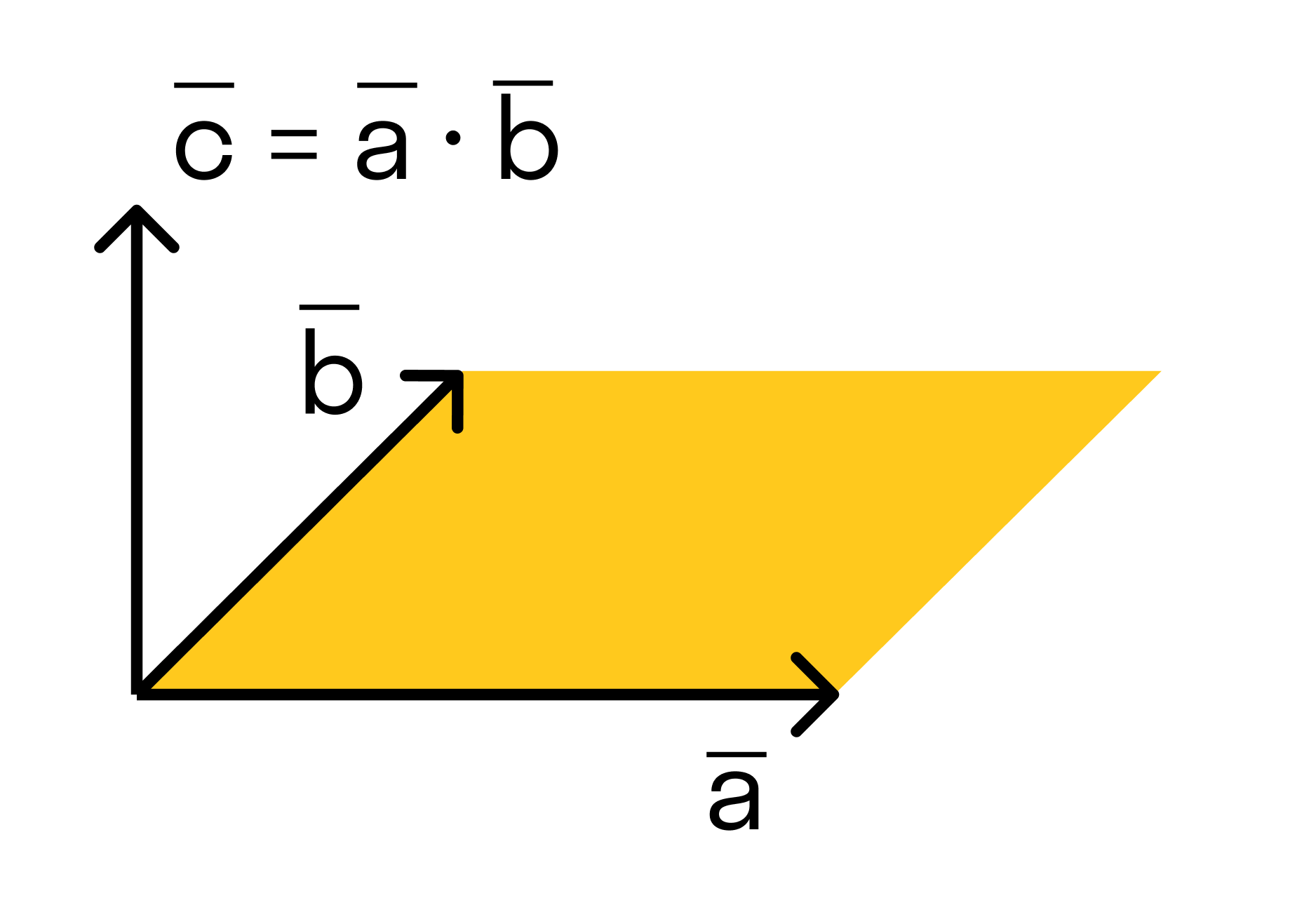
Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.
Векторное произведение двух векторов a = и b = в декартовой системе координат — это вектор, значение которого можно вычислить, используя формулы вычисления векторного произведения векторов:
Векторное произведение векторов →a и →b обозначается как [→a • →b].
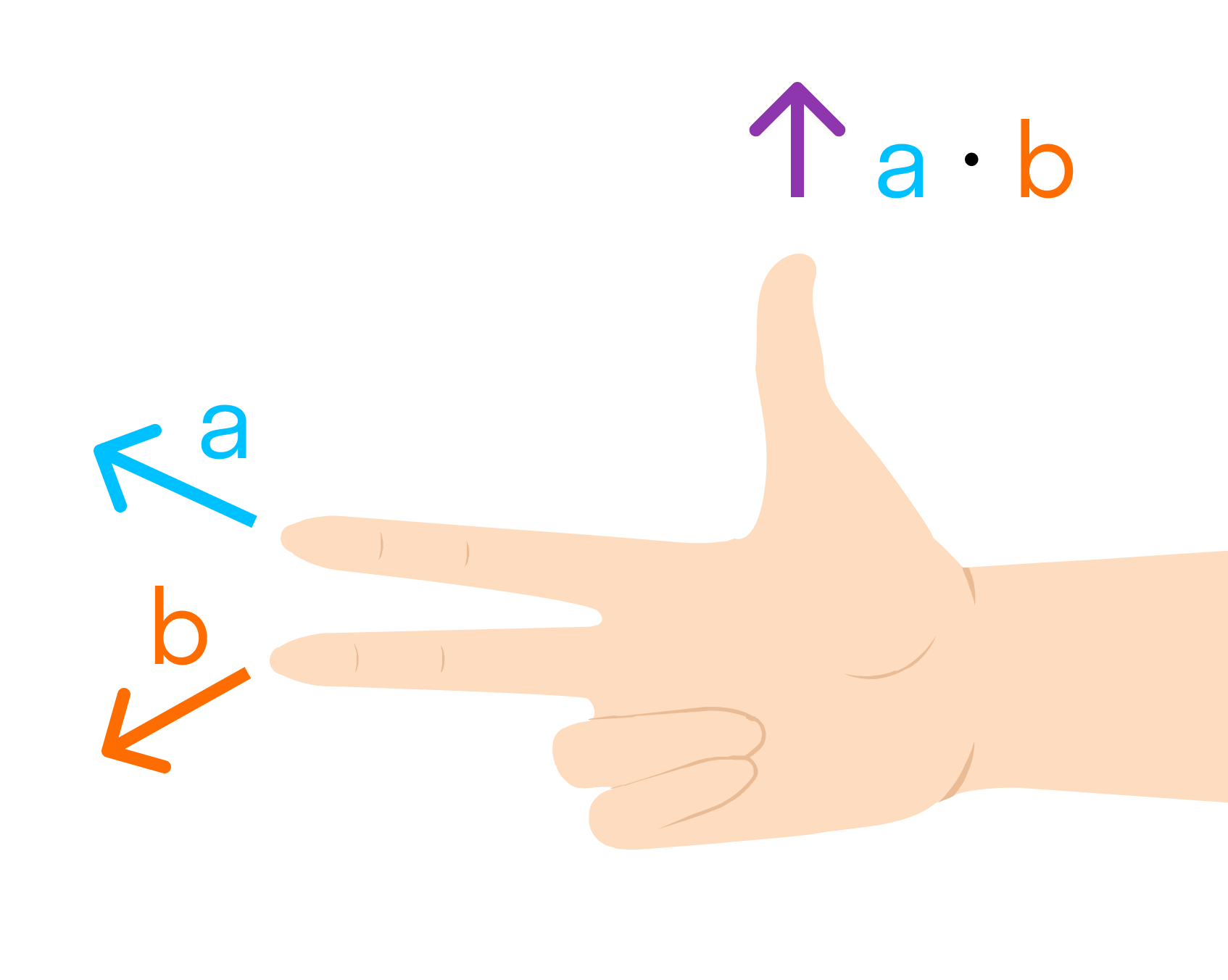
Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.
Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.
Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:
- Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
- Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
- Если определитель равен нулю, то векторы компланарны (линейно зависимы).
Координаты векторного произведения
Рассмотрим векторное произведение векторов в координатах.
Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.
В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор
→i, →j, →k — координатные векторы.
Это определение показывает нам векторное произведение в координатной форме.
Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:
Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:
Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.
Свойства векторного произведения
Векторное произведение в координатах представляется в виде определителя матрицы:
На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:
- Антикоммутативность
- Свойство дистрибутивности
Сочетательное свойство
, где λ произвольное действительное число.
Для большей ясности докажем свойство антикоммутативности векторного произведения.
Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому
что доказывает свойство антикоммутативности векторного произведения.
Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.
Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).
Примеры решения задач
Пример 1
а) Найти длину векторного произведения векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
б) Найти площадь параллелограмма, построенного на векторах →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
а) По условию требуется найти длину векторного произведения. Подставляем данные в формулу:
Так как в задаче речь идет о длине, то в ответе указываем размерность — единицы.
б) По условию требуется найти площадь параллелограмма, который построен на векторах →a и →b. Площадь такого параллелограмма численно равна длине векторного произведения:
Пример 2
Найти |[-3→a x 2→b]|, если |→a| = 1/2, |→b| = 1/6, ∠(→a, →b) = π/2.
По условию снова нужно найти длину векторного произведения. Используем нашу формулу:
Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
Выносим константу за пределы модуля, при этом модуль позволяет убрать знак минус. Длина же не может быть отрицательной.
Пример 3
Даны вершины треугольника A (0, 2, 0), B (-2, 5,0), C (-2, 2, 6). Найти его площадь.
Сначала найдём векторы:
Затем векторное произведение:
Вычислим его длину:
Подставим данные в формулы площадей параллелограмма и треугольника:
Геометрический смысл векторного произведения
По определению длина векторного произведения векторов равна
А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.
Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.
Физический смысл векторного произведения
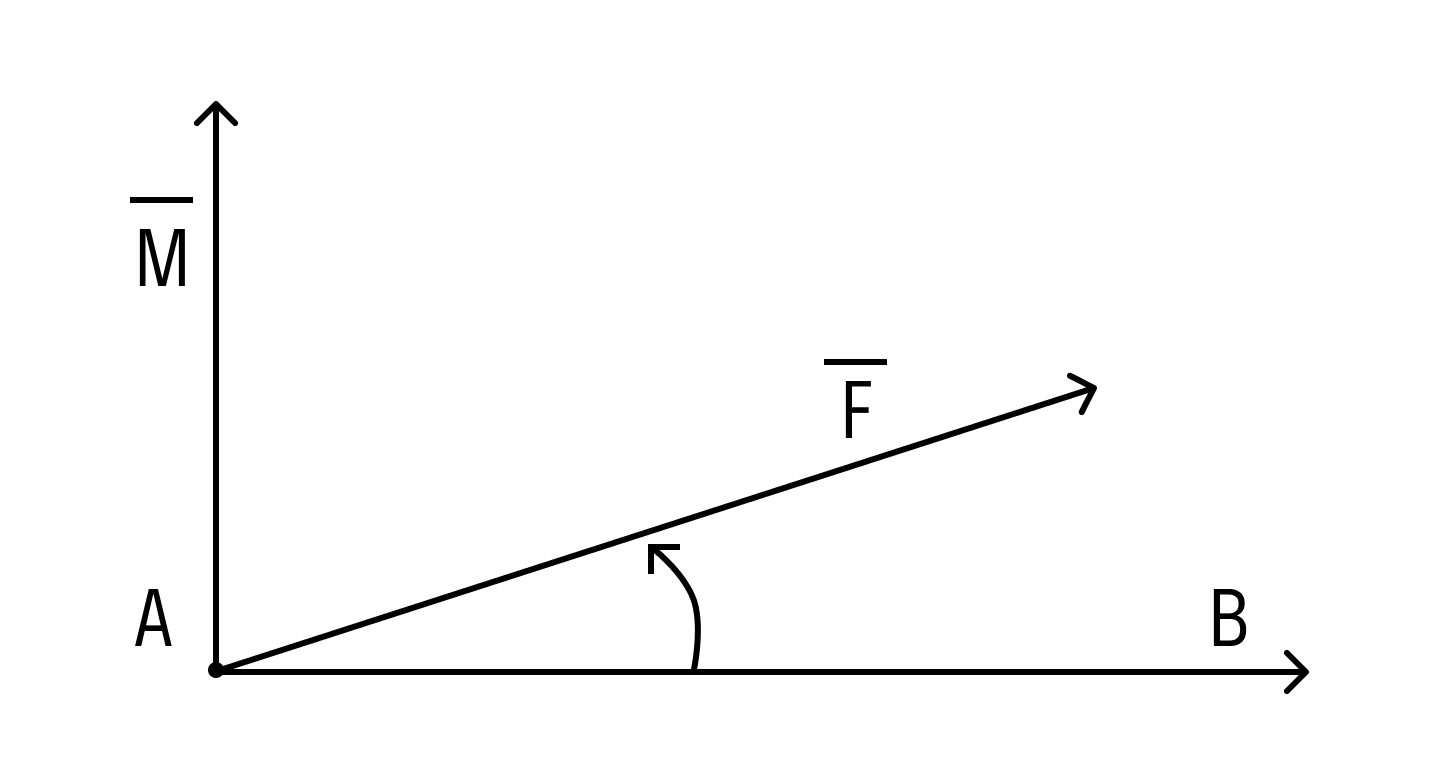
В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.
Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F].
Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.