1000 градусов на окружности

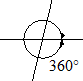
Когда прямые пересекаются, то получается четыре разные области по отношению к точке пересечения.
Эти новые области называют углами.

На картинке видны 4 разных угла, образованных пересечением прямых AB и CD

Обычно углы измеряются в градусах, что обозначается как °. Когда объект совершает полный круг, то есть движется из точки D через B, C, A, а затем обратно к D, то говорят что он повернулся на 360 градусов (360°). Таким образом, градус — это $frac$ круга.

Видео:ПОЧЕМУ АБСОЛЮТНЫЙ НОЛЬ -273.15 °C?Скачать

Углы больше 360 градусов

Мы говорили о том, что когда объект делает полный круг вокруг точки, то он проходит 360°, однако, когда объект делает более одного круга, то он делает угол более 360 градусов. Это обычное явление в повседневной жизни. Колесо проходит многие круги, когда автомобиль движется, то есть оно образует угол больше 360°.

Для того, чтобы узнать количество циклов (пройденных кругов) при вращении объекта, мы считаем количество раз, которое нужно прибавить 360 к самому себе, чтобы получить число равное или меньшее, чем данный угол. Точно так же мы находим число, которое мы умножаем на 360, чтобы получить число меньшее, но наиболее близкое к данному углу.

Пример 2
1. Найти количество кругов, описанных объектом, образующем угол
a) 380°
b) 770°
c) 1000°
Решение
a) 380 = (1 × 360) + 20
Объект описал один круг и 20°
Так как $20^ = frac = frac$ круга
Объект описал $1frac$ кругов.

b) 2 × 360 = 720
770 = (2 × 360) + 50
Объект описал два круга и 50°
$50^ = frac = frac$ круга
Объект описал $2frac$ круга
c)2 × 360 = 720
1000 = (2 × 360) + 280
$280^ = frac = frac$ кругов
Объект описал $2frac$ кругов

Видео:Если она нагреется до 1000 градусов, всем ханаСкачать

Положительные и отрицательные углы

Когда объект вращается по часовой стрелки, то он образует отрицательный угол вращения, а когда вращается против часовой стрелке — положительный угол. До этого момента мы рассматривали только положительные углы.

В форме диаграммы отрицательный угол может быть изображен так, как это показано ниже.

Рисунок ниже показывает знак угла, который измеряется от общей прямой, 0 оси (оси абсцисс — х оси)

Это означает, что при наличии отрицательного угла, мы можем получить соответствующий ему положительный угол.
Например, нижняя часть вертикальной прямой это 270°. Когда измеряется в негативную сторону, то получим -90°. Мы просто вычитаем 270 из 360. Имея отрицательный угол, мы прибавляем 360, для того чтобы получить соотвествующий положительный угол.
Когда угол равен -360°, это означает, что объект совершил более одного круга по часовой стрелке.

Пример 3
1. Найти соответствующий положительный угол
a) -35°
b) -60°
c) -180°
d) — 670°

2. Найти соответствующий отрицательный угол 80°, 167°, 330°и 1300°.
Решение
1. Для того, чтобы найти соответствующий положительный угол мы прибавляем 360 к значению угла.
a) -35°= 360 + (-35) = 360 — 35 = 325°
b) -60°= 360 + (-60) = 360 — 60 = 300°
c) -180°= 360 + (-180) = 360 — 180 = 180°
d) -670°= 360 + (-670) = -310
Это означает один круг по часовой стрелке (360)
360 + (-310) = 50°
Угол равен 360 + 50 = 410°

2. Для того, чтобы получить соответсвующий отрицательный угол мы вычитаем 360 от значения угла.
80° = 80 — 360 = — 280°
167° = 167 — 360 = -193°
330° = 330 — 360 = -30°
1300° = 1300 — 360 = 940 (пройден один круг)
940 — 360 = 580 (пройден второй круг)
580 — 360 = 220 (пройден третий круг)
220 — 360 = -140°
Угол равен -360 — 360 — 360 — 140 = -1220°
Таким образом 1300° = -1220°

Видео:Что такое радиан | Почему в круге 360 | Профильный ЕГЭ математикаСкачать

Радиан

Радиан — это угол из центра круга, в который заключена дуга, длина которой равна радиусу данного круга. Это единица измерения угловой величины. Такой угол примерно равен 57,3°.
В большинстве случаев, это обозначается как рад.
Таким образом $1 рад approx 57,3^$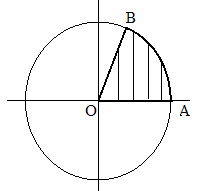

Радиус = r = OA = OB = AB
Угол BOA равен одному радиану

Поскольку длина окружности задается как $2pi r$, то в окружности $2pi$ радиусов, а значит в целом круге $2pi$ радиан.

Радианы обычно выражаются через $pi$ во избежание десятичных частей в вычислениях. В большинстве книг, аббревиатура рад (rad) не встречается, но читатель должен знать, что, когда речь идет об угле, то он задан через $pi$, а единицами измерения автоматически становятся радианы.

Пример 4
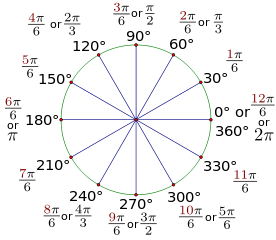
1. Преобразовать 240°, 45°, 270°, 750° и 390° в радианы через $pi$.
Решение
Умножим углы на $frac$.

2. Преобразовать следующие углы в градусы.
a) $fracpi$
b) $3,12pi$
c) 2,4 радиан
Решение
$180^ = pi$
a) $frac pi = frac times 180 = 225^$
b) $3,12pi = 3,12 times 180 = 561,6^$
c) 1 рад = 57,3°
$2,4 = frac = 137,52$

Отрицаетльные углы и углы больше, чем $2pi$ радиан

Для того чтобы преобразовать отрицательный угол в положительный, мы складываем его с $2pi$.
Для того чтобы преобразовать положительный угол в отрицательный, мы вычитаем из него $2pi$.

Пример 5
1. Преобразовать $-fracpi$ и $-fracpi$ в позитивные углы в радианах.

Решение
Прибавляем к углу $2pi$
$-fracpi = -fracpi + 2pi = fracpi = 1fracpi$

Когда объект вращается на угол больший, чем $2pi$;, то он делает больше одного круга.
Для того, чтобы определить количество оборотов (кругов или циклов) в таком угле, мы находим такое число, умножая которое на $2pi$, результат равен или меньше, но как можно ближе к данному числу.

Пример 6
1. Найти количество кругов пройденных объектом при данных углах
a) $-10pi$
b) $9pi$
c) $fracpi$

Решение
a) $-10pi = 5(-2pi)$;
$-2pi$ подразумевает один цикл в направлении по часовой стрелке, то это означает, что
объект сделал 5 циклов по часовой стрелке.

b) $9pi = 4(2pi) + pi$, $pi =$ пол цикла
объект сделал четыре с половиной цикла против часовой стрелки

c) $fracpi=3,5pi=2pi+1,5pi$, $1,5pi$ равно три четверти цикла $(frac=frac)$
объект прошел один и три четверти цикла против часовой стрелки

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Тысячная, формулы тысячной для определения расстояний и дальности, простейшие способы измерения углов на местности с помощью тысячных.

В туристском походе, путешествии и в других случаях часто возникает потребность в определении расстояний до недоступных предметов, измерении их длины и высоты. В определении шириныреки или другого препятствия, в определении высоты дерева, в подсчете оставшегося пути до конечной цели. В этих случаях поможет тысячная.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Тысячная, формулы тысячной для определения расстояний и дальности, простейшие способы измерения углов на местности с помощью тысячных.

В войсковой практике, где при вычислениях постоянно приходится пользоваться соотношениями между угловыми и линейными величинами, вместо градусной системы мер применяется артиллерийская (линейная). Более простая и удобная для быстрых приближенных вычислений. За единицу угловых мер артиллеристы принимают центральный угол круга, стянутого дугой, равной 1/6000 длины окружности.

Этот угол называется делением угломера, так как используется во всех артиллерийских угломерныхприборах. Иногда этот угол называют тысячная. Это название объясняется тем, что длина дуги такого угла по окружности равна приближенно тысячной доле ее радиуса. Это очень важное обстоятельство.

Следовательно, при наблюдении окружающих нас объектов, мы находимся как бы в центре концентрических окружностей, радиусы которых равны расстояниям до объектов. И мерой центральных углов будут служить линейные отрезки, равные тысячной доле расстояния до объектов. Так, если дом длиной 5 метров расположен на удалении от наблюдателя на 1000 метров, то он укладывается в центральный угол, равный пяти тысячным. Такой угол записывается на бумаге так : 0-05, и читается ноль, ноль пять.

Если длина забора равна 100 метрам, то он укладывается в центральный угол, равный 100 тысячным, одно большое деление угломерного прибора. Записывается этот угол на бумаге так : 1-00 тысячная, и читается один, ноль. Из этих примеров видно, что углы позволяют очень быстро и легко посредством простейших арифметических действий переходить из угловых измерений к линейным и обратно.

Так, например, если рядом с домом, находящимся от наблюдателя на расстоянии Д-1500 метров (Д дальность) находится дерево и угол между ними укладывается в пятьдесят пять тысячных У=0-55 (У угол) и требуется определить расстояние от дома до дерева В (В расстояние), то из пропорции В : Д = У : 1000 вытекает формула для определения линейных размеров.

Видео:Что такое радиан?Скачать

В = Д х У / 1000 = 1500 х 55 / 1000 = 82,5 метра.

Из этой же пропорции можно вывести формулу тысячной и для определения дальности до объектов.

Видео:Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать

Д = 1000 х В / У

Решим простой пример определения расстояния через формулу тысячной у столба высотой 6 метров вы видите человека. Требуется определить расстояние до него. Вначале определяем, в какой угол укладывается высота столба. Допустим, что высота столба укладывается в угол У=0—05 (пять тысячных). Тогда по формуле для определения дальности получим : Д = 1000 х 6 / 5 = 1200 метров.

Использование двух вышеприведенных формул позволяет определять быстро и точно любые линейные и угловые величины на местности.

Между делениями угломера (в тысячных) и обычной градусной системой угловых мер существуют соотношения : одна тысячная 0-01 равна 3,6′ (минуты), а большое деление угломера (1-00) = 6 градусов. Эти соотношения позволяют при необходимости осуществлять переход от одной системы измерений к другой.

Видео:Радианная мера угла. 9 класс.Скачать

Простейшие способы измерения углов на местности с помощью тысячных.

Углы на местности можно измерять с помощью полевого бинокля, линейки и подручных предметов. В поле зрения бинокля имеются две взаимно-перпендикулярные угломерные шкалы для измерения горизонтальных и вертикальных углов. Величина одного большого деления этих шкал соответствует 0-10, а малого 0-05 тысячных.

Для измерения угла между двумя направлениями надо, глядя в бинокль, совместить какой-либо штрих угломерной шкалы с одним из этих направлений и подсчитать число делений до второго направления. Так, например, отдельноедерево (пулемет противника) расположено влево от дороги на угол 0-30.

Вертикальной шкалой пользуются при определении вертикальных углов. В случае их больших размеров можно пользоваться и горизонтальной шкалой, повернув бинокль вертикально. При отсутствиибинокля углы можно измерять обычной линейкой с миллиметровыми делениями. Если такую линейку держать перед собой на расстоянии 50 см от глаз, то одно ее деление (1 мм) будет соответствовать углу в две тысячных (0-02).

Точность измерения углов таким способом зависит от навыка в вынесении линейки точно на 50 см от глаза. Этого можно достигнуть, привязав к линейке нитку и закусив ее зубами на расстоянии 50 см. С помощью линейки можно измерять углы и в градусах. В этом случае ее следует выносить на расстояние 60 см от глаза. Тогда 1 см на линейке будет соответствовать углу в 1 градус.

При отсутствии линейки с делениями можно использовать пальцы, ладонь или любой небольшойпредмет (спичечную коробку, карандаш), размер которых в миллиметрах, а следовательно, и в тысячных известен. Такая мерка выносится на расстояние 50 см от глаза и по ней путем сравнения определяется искомая величина угла.

По материалам книги «Карта и компас мои друзья».
Клименко А.И.

Видео:Почему в окружности именно 360 градусов?Скачать

Алгебра

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Видео:Как искать точки на тригонометрической окружности.Скачать

Числовая и единичная окружность

В средней школе мы уже познакомились с координатной, или числовой прямой. Так называют абстрактную прямую, на которой выбрана точка отсчета, определен единичный отрезок, а также задано направление, в котором следует откладывать положительные числа. С помощью координатной прямой удается наглядно представлять сложение и вычитание как положительных, так и отрицательных чисел, решать задачи, связанные с перемещением по прямой, и делать многое другое.

Однако порою приходится рассматривать задачи, связанные с движением по окружности, а также складывать и вычитать углы. Здесь математикам помогает другая абстракция – числовая окружность. Пусть два гонщика (Вася и Петя) едут по круговой трассе, чья протяженность составляет 1 км. За минуту Вася проехал 1250 м, а Петя преодолел только 500 м. Попытаемся показать их положение графически.

Построим на координатной плоскости окружность с центром в начале координат длиной 1 км. Будем считать, старт находится в крайней правой точке трассы, на пересечении оси Ох и окружности. Также условимся, что гонщики едут против часовой стрелки. Тогда получим такую картинку:

Петя проедет ровно половину окружности и окажется в крайней левой точке трассы. Вася же за минуту успел сделать полный круг (1 км) и проехать ещё 250 м, а потому оказался в верхней точке.

Теперь предположим, что Петя стоит на месте, а Вася проехал ещё 250 м (четверть круга). В результате оба пилота оказались в одной точке, но проехали они разное расстояние! Получается, что по положению гонщика невозможно однозначно определить, сколько именно метров он проехал.

Заметим, что очень удобно характеризовать положение точки на числовой окружности с помощью угла. Достаточно соединить точку отрезком с началом координат. Полученный отрезок образует с прямой Ох некоторый угол α:

В тригонометрии предпочитают использовать особую числовую прямую, радиус которой равен единице. По ряду причин, которые станут ясны чуть позже, с ней очень удобно работать. Такую фигуру называют единичной окружностью.

Выглядит единичная окружность так:

Видео:Как решают уравнения в России и СШАСкачать

Откладывание углов на единичной окружности

Положение каждой точки на единичной окружности можно указать с помощью угла. Пусть надо найти точку, соответствующую углу 60°. Для этого просто строим угол следующим образом:

Углы, которые откладывают на единичной окружности, называют углами поворота. В данном случае можно утверждать, что точке А соответствует угол поворота, равный 60°.

Отложить можно и угол, больший 90° и даже 180°. Выглядеть они будут примерно так:

Углы можно складывать друг с другом и вычитать. Предположим, нам надо построить угол, равный сумме углов 120° и 110°. Для этого сначала совершить поворот на 120°, а потом от полученного отрезка отложить ещё один угол в 110°:

Ясно, что возможно построить любой угол в диапазоне от 0° до 360°. А можно ли отложить угол, который будет больше 360°? В обычной планиметрии мы не работаем с такими углами, однако в тригонометрии они существуют. Действительно, мы же можем, например, сложить углы 250° и 140°. В итоге получится 250 + 140 = 390°:

В результате мы совершили полный оборот (360°) и вдобавок повернули отрезок ещё на 30°. Получается, что углам в 390° и 30° соответствует одна и та же точка.

Углы можно и вычитать друг из друга. Для этого вычитаемый угол надо отложить в противоположном направлении – не против часовой, а по часовой стрелке. Например, вычитая из 150° угол в 70°, придем в точку, соответствующую 150 – 70 = 80°:

Из арифметики мы помним, что вычитание можно заменить прибавлением противоположного (то есть отрицательного) числа:

Получается, что отложив угол 70° по часовой стрелке, мы прибавили к 150° отрицательный угол (– 70°). То есть на единичной окружности можно откладывать отрицательные углы! Для их получения поворот надо осуществлять по часовой стрелке. Например, угол – 60° будет выглядеть так:

Итак, мы можем откладывать и положительные, и отрицательные углы, а также углы, большие 360°. Вообще в тригонометрии угол может быть равен любому действительному числу. На единичной окружности можно отложить углы величиной 1000°, 1000000° и (– 999999999°) и любые другие, самые большие и самые малые углы. В этом смысле единичная окружность схожа с координатной прямой. Разница лишь в том, что на прямой разным числам всегда соответствуют разные точки, а на окружности разным углам могут соответствовать одни и те же точки.

Ещё раз отметим, что один полный оборот равен 360°. Если отложить на окружности произвольную точку А, которой соответствует угол α, а потом добавить к α ещё 360°, то мы попадем в ту же самую точку:

С точки зрения тригонометрии те углы поворота, которые соответствуют одной точке на единичной окружности, равны друг другу. Поэтому можно записать формулу:

Естественно, при вычитании 360° из угла мы тоже совершим полный поворот, только по часовой стрелке, поэтому верна и другая запись:

Угол, не изменится и в том случае, если мы совершим не один, а два полных оборота, то есть добавим к нему 2•360° = 720°. Можно добавлять к углу два, три, четыре полных поворота, но он не изменится от этого. Обозначим буквой n количество оборотов, которые мы добавляем к углу. Естественно, что n – целое число. Справедливой будет формула:

Например, верны следующие равенства:

15° + 3•360° = 15° + 1080° = 1095°

100° + 10•360° = 100° + 3600° = 3700°

1000° = 1000° – 2•360° = 1000° – 720° = 280°

Очевидно, что любой точке на окружности соответствует какой-то угол α из промежутка 0 ≤ α 1 5

📸 Видео

Тысячные (мера измерения плоского угла) в военной топографии и артиллерииСкачать

Деление окружности на 3; 6; 12 равных частейСкачать

ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН: общее определение угла, измерение дуг и угловСкачать

Двигатели устойчивые к температуре в 1000 °C // Большой скачокСкачать

Длина окружности. Математика 6 класс.Скачать

MrBeast ослепил 1000 людей - реакция Градуса и РаймаСкачать

Котика ударило током, 10 т. ВольтСкачать

ЧТО ЕСЛИ ЗАМОК РАСКАЛИТЬ ДО 1000 ГРАДУСОВ и ОТКРЫТЬ ?!Скачать

ДЛИНА ОКРУЖНОСТИ и ПЛОЩАДЬ КРУГА 9 класс геометрия АтанасянСкачать