Классификация четырехугольников формируемая у учащихся после изучения данной темы

В учебниках А. В. Погорелова, Л. С. Атанасяна и др. методика введения понятия четырехугольника различна, хотя трактовка четырехугольника в этих учебниках одинакова.

В учебнике А. В. Погорелова (8 кл.) понятие четырехугольника вводится непосредственно его определением.

Onp. 1. Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек нс должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.

Данные точки называются вершинами четырехугольника, а соединяющие их отрезки — сторонами четырехугольника.

В учебнике Л. С. Атанасяна и др. (8 кл.) введению этого понятия предшествуют понятия многоугольника, внутренней и внешней области многоугольника, выпуклого многоугольника, а также теорема о сумме углов п -угольника. (В учебнике А. В. Погорелова эти факты рассматриваются позже.)

В учебнике говорится, что каждый четырехугольник имеет четыре вершины, четыре стороны и две диагонали. Две несмежные стороны четырехугольника называются противоположными. Две вершины, не являющиеся соседними, называются также противоположными. Сообщается, что четырехугольники бывают выпуклыми и невыпуклыми.

а) Методика введении понятии четырехугольника. Учащиеся уже знакомы с некоторыми видами четырехугольников, поэтому перед тем как ввести понятие четырехугольника, можно предложить им построить любой четырехугольник. Рассматривая построенные фигуры, учащиеся делают вывод: четырехугольник — фигура, образованная четырьмя точками и четырьмя отрезками, последовательно соединяющими эти точки.

Затем можно предложить упражнения на распознавание четырехугольников типа: Какие из фигур, изображенных на рис. 74 являются четырехугольниками?

Фигура, изображенная на рис. 74в, образована четырьмя точками и четырьмя отрезками, последовательно соединяющими их, но три точки А, В, С лежат на одной прямой. Фигуру на рис. 746 образуют четыре точки А, В, С, Д никакие три из них нс лежат на одной прямой, и четыре отрезка, но отрезки AD и ВС пересекаются. Такие фигуры, хотя и образованы четырьмя точками и четырьмя отрезками, последовательно их соединяющими, не относят к четырехугольникам.

Так постепенно уточняется содержание понятия четырехугольника. Затем вводятся понятия соседних и противолежащих вершин, диагоналей четырехугольника, соседних и противолежащих сторон.

Возможен и другой подход к введению четырехугольника: учитель с помощью мультимедиапроектора показывает учащимся изображения различных фигур: треугольников, четырехугольников, пятиугольников и т. д., и просит их выделить фигуры, образованные по одному и тому же признаку. В процессе анализа фигур учащиеся постепенно выделяют сами содержание понятия четырехугольника.

Конкретные подходы могут быть разными, но важно, чтобы учащиеся сами принимали активное участие в анализе содержания изучаемого понятия.

В учебнике Л. С. Атанасяна и др. четырехугольник вводится как частный случай многоугольника. Такой подход по сравнению с подходом в учебниках А. В. Погорелова, А. Д. Александрова и др. является менее удачным, так как общее понятие многоугольника используется только в конце 9 класса, использовать же это понятие для введения четырехугольника нецелесообразно, так как понятие четырехугольника проще понятия многоугольника.

б) Методика изучения параллелограмма. В разных учебниках геометрии можно увидеть разные определения параллелограмма. С точки зрения психологии, как уже подчеркивалось нами в предыдущих лекциях, наиболее удачным является определение параллелограмма как четырехугольника, у которого противоположные стороны попарно параллельны. Такое определение позволяет быстро представить себе образ определяемого объекта.

Перед введением понятия можно выполнить упражнение на построение четырехугольника, у которого противоположные стороны попарно параллельны. Затем рассмотреть упражнения на распознавание объектов, принадлежащих понятию «параллелограмм». Среди предлагаемых объектов должны быть четырехугольники, у которых одна пара, ни одной пары, две пары противоположных параллельных сторон, в том числе — прямоугольник, ромб, квадрат.

Целесообразны упражнения на построение четырехугольников и доказательство принадлежности их к параллелограмму. Приведем пример.

Начертите четырехугольник ABCD так, чтобы ZA = 6(Р, ZB = 120°, ZC = 6(j и выясните, является ли он параллелограммом.

Подобные упражнения имеются в учебнике Л. С. Атанасяна и др.

В учебной литературе используются различные последовательности изложения свойств и признаков параллелограмма. В учебнике Л. С. Атанасяна и др. излагаются свойства параллелограмма, а затем их признаки.

Свой cm ва параллелограмма:

• 1. В параллелограмме противоположные стороны равны и противоположные углы равны.
• 2. Диагонали параллелограмма точкой пересечения делятся пополам.

При знаки параллелограмма:

• 1. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм.
• 2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
• 3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник параллелограмм.

В других учебниках излагаются сначала признаки, а затем свойства параллелограмма (А. В. Погорелов).

Свойства параллелограмма могут быть сформулированы самими учащимися в процессе выполнения упражнений. Например, свойство сторон параллелограмма может быть выделено в результате выполнения упражнения:

1. A BCD — параллелограмм. Доказать, что Д АВС = ACDA.

Это упражнение моделирует и доказательство этого свойства.

Перед изучением свойств углов параллелограмма можно выполнить упражнение:

2. В параллелограмме A BCD /.А = 60°. Вычислить все его углы.

Выполнение этого упражнения основывается на определении параллелограмма и свойстве параллельных прямых. Решив задачу, учащиеся замечают, что противоположные углы параллелограмма равны, а сумма углов, прилежащих к одной стороне параллелограмма, равна 180°.

Это упражнение дает другой, отличный от представленных в учебниках, способ доказательства теоремы о свойстве углов параллелограмма. В учебниках доказательство основано на признаках равенства треугольников. Оно может быть таким: ZА + /.В = 180°, ZC + /.В = 180° (по свойству внутренних односторонних углов), следовательно, /.А = ZC.

Если в учебнике изложение теории начинается со свойств параллелограмма, то признаки будут выступать как теоремы, обратные изученным теоремам. Если изложение начинается с признака, то естественна постановка проблемы: отыскать четырехугольник, являющийся параллелограммом.

Следует подчеркнуть практическую значимость изучения признаков параллелограмма. Они позволяют активнее решать различные задачи, владеть критериями распознавания параллелограммов. Каждый из признаков может служить определением параллелограмма. Тогда определение параллелограмма надо будет доказывать как теорему.

В ходе изучения параллелограмма рассматриваются его частные виды: прямоугольник, ромб, квадрат. Ознакомление учащихся с ними можно осуществить через упражнения на их построение. Например, можно выполнить упражнение на построение параллелограмма, у которого углы прямые. Далее формулируется определение прямоугольника и выявляется его специфическое свойство: диагонали прямоугольника равны. Верно и обратное утверждение: если диагонали параллелограмма равны, то он — прямоугольник. Поэтому прямоугольник можно определить и так: это — параллелограмм, у которого диагонали равны. За таким определением было бы очень трудно видеть объекты, относящиеся к прямоугольнику, но познакомить учащихся с этим признаком полезно.

Аналогично, при изучении ромба следует рассмотреть его признаки:

1. Если диагонали параллелограмма перпендикулярны, то он является ромбом.

2. Если у параллелограмма диагонали являются биссектрисами его углов, то он — ромб.

Определения прямоугольника, ромба, квадрата, содержащиеся в учебнике, являются обычно избыточными, то есть содержат лишние свойства. Например, прямоугольник определяется как параллелограмм, у которого все углы прямые. Такое определение избыточное: можно указать только один прямой угол. Тогда, используя свойство параллелограмма, легко доказать, что и другие три угла также будут прямыми. Однако в целях простоты создания наглядного адекватного образа параллелограмма используется указанное избыточное определение. Итогом изучения может быть классификация параллелограммов (таблица 13).

» —__^Г1о сторонам По углам

Параллелограмм, не являющийся ромбом

Параллелограмм, не являющийся прямоугольником

в) Методика изучения трапеции и её свойств. При изучении параллелограмма можно обратить внимание учащихся на четырехугольник, у которого только две противоположные стороны параллельны. Такой четырехугольник называется трапецией. При изучении свойств трапеции центральное место занимает теорема о средней линии. Однако в учебнике нет ни одного упражнения

на усвоение понятия средней линии трапеции. Подвести учащихся к теореме можно, предложив упражнение:

Доказать, что средняя линия треугольника А BE является средней линией трапеции ABCD (рис. 75).

Это упражнение позволяет учащимся «открыть» теорему о средней линии трапеции и способ её доказательства. Учащиеся могут предложить и другие способы доказательства теоремы, например, разбить трапецию се диагонатыо на два треугольника и затем доказать, что отрезки, заключенные между диагональю и боковыми сторонами трапеции, являются средними линиями образуемых треугольников и т. д.

При изучении четырехугольников сеть возможность осуществлять интеграцию алгебраического и геометрического методов и формировать при этом целостные знания учащихся о параллелограмме, трапеции и других частных видах четырехугольников. Проиллюстрируем этот подход на примере формирования понятия трапеции, выделив его основные этапы.

• 1 этап (мотивация введения понятия трапеции) реализуется традиционно, поэтому мы не будем останавливаться на нем подробно.
• 2 этап. Ознакомление с существенными свойствами трапеции па геометрическом языке может осуществляться так: заранее готовится рисунок с изображением разных многоугольников, в том числе и трапеции. Он может быть

выполнен на доске или спроецирован на экран с помощью мультимедийного проектора. Перед учащимися ставится вопрос, какие из фигур, изображенных на рисунке, имеют общие свойства? Учащиеся замечают, что в некоторых четырехугольниках две противоположные стороны параллельны, а две другие нет. Затем им сообщается, что такой четырехугольник называется трапецией. Здесь же можно сказать, что описанный четырехугольник вместе с его внутренней областью также называют трапецией

После выделения существенных свойств трапеции учащиеся под руководством учителя, используя конкретные примеры, переводят эти свойства на алгебраический язык и задают трапецию системой неравенств:

Как мы видим, система состоит из четырех линейных неравенств с двумя переменными. В двух неравенствах коэффициенты при х равны, что означает параллельность двух сторон трапеции.

С помощью конкретных примеров учащиеся самостоятельно выясняют, что в зависимости от расположения трапеции возможно различное задание ее в виде системы неравенств. В случае, если: 1) основания трапеции параллельны оси OY (рис. 76 а); 2) трапеция симметрична относительно оси OY (рис. 76 б, в); 3) в качестве боковых сторон трапеции выступают отрезки осей ОХ и OY (рис. 76 г, д), трапеция может быть задана соответственно системой неравенств:

причем, а| Ь > 0, а > О, С ^ • п наити площадь трапеции.

Если да, то запишите се уравнение.

Следующие задачи предлагаются после изучения векторов.

• 3. На сторонах АВ и ВС треугольника АВС отмечены соответственно точки М и Н так, что АВ = ЗВМ, ВС = 3BN. Используя векторы, докажите, что АСНМ — трапеция.
• 4. Используя векторы, докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен ее основаниям и равен полуразности оснований.
• 5. В трапеции ABCD основание AD в три раза больше основания ВС. На

стороне AD отмечена точка К, такая, что AK=-AD. Выразите векторы СК, KD и ВС через векторы а = ВА и b = CD.

Аналогично, по такой же схеме, сочетая геометрические действия с алгебраическими, можно проводить формирование понятия параллелограмма и его частных видов (ромба, прямоугольника, квадрата).

Таким образом, формирование математических понятий в условиях единства алгебраического и геометрического методов сводится к следующим действиям:

• 1) одновременная трактовка понятия на геометрическом и алгебраическом (буквенно-символическом) языках;
• 2) распознавание объектов, принадлежащих понятию и представленных как в алгебраической, так и геометрической формах;
• 3) выведение следствий из факта принадлежности объекта данному понятию, в случае, если этот объект представлен в геометрической и алгебраической формах;
• 4) решение задач и упражнений на применение данного понятия параллельно алгебраическим и геометрическим методами или методом, включающим в себя действия, связанные с геометрическим образом данного понятия и его алгебраической трактовкой вместе.

В целом взаимосвязь алгебраического и геометрического методов позволяет формировать понятия в единстве алгебраических и геометрических действий, адекватных этому виду знаний, создавая тем самым у учащихся целостное представление о каждом изучаемом понятии.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

КУРСОВАЯ РАБОТА на тему «Методика изучения четырехугольников в основной школе»

В современной школе в связи с появлением новых учебников, новых подходов к изложению материала, возрастает интерес как к математическому образованию в целом, так и к вопросам преподавания математики, в частности геометрии.

Изучение четырехугольников в курсе геометрии основной школы является разделом традиционным и достаточно важным во всех периодах школьного образования. В курсе геометрии 7-9-х классов данная тема является весьма актуальной, так как на рассмотренном материале, как на фундаменте, строят и изучают другие разделы геометрии: преобразование фигур, площади, многоугольники. Кроме того, изучение многогранников, площадей и объемов также базируется на этой теме.

Видео:Математика 5 класс (Урок№29 - Четырёхугольники.)Скачать

Скачать:

Видео:Миникурс по геометрии. ЧетырехугольникиСкачать

Предварительный просмотр:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ

Федеральное государственное автономное образовательное учреждение

Высшего профессионального образования «Казанский (Приволжский)

ИНСТИТУТ МАТЕМАТИКИ И МЕХАНИКИ ИМ. Н.И.ЛОБАЧЕВСКОГО

КАФЕДРА ТЕОРИИ И ТЕХНОЛОГИЙ ПРЕПОДАВАНИЯ

МАТЕМАТИКИ И ИНФОРМАТИКИ

44.03.05 «Педагогическое образование

(математическое образование, информатика и информационные технологии)»

Методика изучения четырехугольников

в основной школе

Студент 3 курса

« » мая 2018 г. Афанасьева Дарья Сергеевна

Доцент, кандидат педагогических наук

« » мая 2018 г. Шакирова Кадрия Бариевна

Логико-дидактический анализ содержания темы «Четырехугольники»…….5

ЛМА темы «Четырехугольники»……………………………………………….7

Описанные и вписанные четырехугольники…………………………………..19

Задачи из ОГЭ повышенной сложности………………………. 23

Методические рекомендации по изучению темы «Четырехугольники»…. 27

План – конспект урока на тему «Прямоугольник»……………………………31

В современной школе в связи с появлением новых учебников, новых подходов к изложению материала, возрастает интерес как к математическому образованию в целом, так и к вопросам преподавания математики, в частности геометрии.

Изучение четырехугольников в курсе геометрии основной школы является разделом традиционным и достаточно важным во всех периодах школьного образования. В курсе геометрии 7-9-х классов данная тема является весьма актуальной, так как на рассмотренном материале, как на фундаменте, строят и изучают другие разделы геометрии: преобразование фигур, площади, многоугольники. Кроме того, изучение многогранников, площадей и объемов также базируется на этой теме.

Между тем при изучении темы «Четырехугольники» возникают определенные трудности:

• при решении задач на построение;
• при применении определений, свойств и признаков четырехугольников к решению практических задач, к доказательству теорем и т. п.

Соответственно возникает необходимость в поиске наиболее эффективных форм и методов работы с теоретическим и задачным материалом по данной теме. В связи с этим цель курсовой работы: исследовать возможности применения методов научного познания при изучении темы «Четырехугольники».

Объектом исследования является процесс обучения геометрии в основной школе.

Предмет исследования – методика обучения по теме «Четырехугольники» в курсе геометрии основной школы.

1. Раскрыть содержание понятий методов научного познания.
2. Изучить учебно-методическую литературу по теме исследования.
3. Показать применение методов научного познания при изучении геометрического материала.
4. Разработать методические рекомендации обучения теме и применить их в учебном процессе

Для реализации цели и задач были использованы следующие методы :

1. Изучение и анализ учебно-методической литературы по теме исследования.
2. Анализ учебника по геометрии 7-9 автора Атанасян Л.С.
3. Проведение практического исследования задач.
4. Разработка урока на тему «Прямоугольник»

Методические рекомендации по изучению темы «Четырехугольники»

§ 2. Параллелограмм и трапеция

Назначение параграфа – ввести понятия параллелограмма и трапеции, рассмотреть свойства и признаки параллелограмма и закрепить полученные знания в процессе решения задач. Следует иметь в виду, что свойства и признаки параллелограмма широко используются в следующих разделах курса, поэтому выработке соответствующих умений и навыков следует уделить серьезное внимание.

Учебный материал можно распределить по урокам следующим образом: параллелограмм, его свойства и признаки – 3 урока, трапеция – 2 урока, задачи на построение циркулем и линейкой – 1 урок.

Определение параллелограмма можно отработать в процессе решения устных задач по заготовленным чертежам.

Теоретический материал п.43 достаточно прост, поэтому доказательство утверждений о свойствах параллелограмма можно предложить учащимся провести самостоятельно (без помощи учебника) на первом же уроке. Для экономии времени можно провести эту работу по вариантам, а затем выслушать учеников, выполнявших разные варианты. Для лучшего усвоения целесообразно решить в классе задачи 376 (а) – устно, 372 (а).

Перед тем как приступить к изучению признаков параллелограмма, следует напомнить учащимся, что означает слово «признак» и что такое обратная теорема. Полезно предложить учащимся сформулировать самим теоремы, обратные утверждениям о свойствах параллелограмма. Нужно подчеркнуть, что если некоторое утверждение верно, то отсюда еще не следует, что верно и обратное утверждение. Обратное утверждение требует отдельного рассмотрения в отношении того, верно оно или нет.

Доказательства утверждений о признаках параллелограмма можно предложить учащимся провести самостоятельно. Для лучшего усвоения доказанных теорем можно решить задачи 379, 382.

На третьем уроке решаются задачи на свойства и признаки параллелограмма. В конце третьего урока целесообразно провести проверочную самостоятельную работу.

Перед изучением п.45 «Трапеция» полезно еще раз вспомнить свойства и признаки параллельных прямых в процессе выполнения устных заданий. В самом п.45 учебника приведены только определения трапеции, ее видов и элементов, а свойства и признаки раскрыты в задачах 386 (свойство средней линии трапеции), 388 (свойство равнобедренной трапеции), 389 (признаки равнобедренной трапеции). Эти задачи необходимо разобрать с учащимися. Это же относится к задаче 385 (теорема Фалеса).

На втором уроке можно провести самостоятельную работу, проверить которую рекомендуется сразу же, например, с помощью мультимедийного оборудования.

Основные требования к учащимся : в результате изучения параграфа учащиеся должны знать и уметь четко формулировать определения параллелограмма и трапеции; уметь формулировать и доказывать утверждения о свойствах и признаках параллелограмма, указывая среди них те, которые являются обратными к уже доказанным утверждениям; знать и уметь обосновывать утверждения о свойствах и признаках равнобедренной трапеции (задачи 388 и 389); уметь решать задачи типа 372 – 377, 379 – 383, 387, 390, 392, решать задачи на построение; должны в ходе изучения темы проявить способность самостоятельно (даже не используя учебник) доказывать утверждения о свойствах и признаках параллелограмма.

§ 3. Прямоугольник, ромб, квадрат.

Назначение параграфа – более детально познакомить учащихся с частными видами параллелограмма – прямоугольником, ромбом и квадратом, их особыми свойствами, а также осевой и центральной симметрией как свойствами некоторых геометрических фигур.

На первом уроке можно изучить п.46 «Прямоугольник», на втором – п.47 «Ромб и квадрат», а третий урок целесообразно посвятить закреплению полученных сведений в процессе решения задач.

Перед изучением темы «Прямоугольник» полезно повторить свойства параллелограмма, признаки равенства прямоугольных треугольников и утверждение о сумме углов выпуклого четырехугольника в процессе решения устных задач.

После того, как сформулировано определение прямоугольника, можно предложить учащимся самим перечислить те его свойства, которыми он обладает, как и любой параллелограмм. Желательно, чтобы они сами доказали утверждение об особом свойстве прямоугольника, а также обратное утверждение (признак прямоугольника). В классе рекомендуется решить задачи 399 (устно), 400, 402.

Перед рассмотрением другого частного вида параллелограмма – ромба полезно провести устную работу по заранее заготовленным чертежам к некоторым задачам.

После введения определения ромба можно предложить учащимся самим сформулировать те его свойства, которые следуют непосредственно из определения, а затем самостоятельно (по вариантам) доказать утверждения об особых свойствах ромба. Полезно обратить внимание учащихся на то, что утверждения, сформулированные в задаче 408 (а, б), являются признаками ромба.

Определение квадрата и его свойства учащиеся могут изучить самостоятельно по учебнику. Затем полезно решить задачу 410. Сделать это можно устно с помощью заранее заготовленных чертежей.

На следующем уроке усвоение изученного материала закрепляется в процессе решения задач. На этом же уроке целесообразно провести самостоятельную работу обучающего характера с проверкой в классе.

Основные требования к учащимся : в результате изучения параграфа учащиеся должны знать и уметь четко формулировать определения прямоугольника, ромба и квадрата; уметь формулировать и доказывать утверждения об особых свойствах прямоугольника и ромба и обратные утверждения (признаки прямоугольника и ромба); уметь решать задачи типа 401-423; в ходе изучения темы должны еще более развить умение самостоятельно обосновывать новые утверждения, опираясь на накопленный опыт.

ЛМА темы «Четырехугольники»

Учебник Геометрия, 7–9 Атанасян Л.С. (Глава V)

Базовые знания: понятие отрезка; смежных и не смежных отрезков; понятие середины отрезка; понятие параллельных прямых; признаки параллельности прямых; понятие угла; понятие градусной меры угла; понятие развернутого угла; понятие прямого угла; понятие смежных и вертикальных углов; понятие перпендикуляра; признаки равенства треугольников; понятие окружности; хорды; радиуса; диаметра.

Базовые умения: умение выполнять построение углов; умение сравнивать отрезки; умение измерять длину отрезка; умение измерять величину угла; умение применять основные теоремы при решении задач на равенство треугольников; умение решать основные геометрические задачи по пройденным ранее темам; умение решать задачи на построение; умение решать задачи, применяя признаки параллельных прямых.

Понятия, вводимые на примерах: понятие многоугольника.

Понятия, вводимые с помощью определения: понятие периметра многоугольника; понятие n – угольника; понятие соседних сторон многоугольника; понятие диагонали многоугольника; понятие выпуклого многоугольника; понятие параллелограмма; понятие трапеции; понятие прямоугольника; понятие ромба; понятие квадрата.

Вводимые свойства: свойства параллелограмма; особое свойство прямоугольника; особое свойство ромба; свойства квадрата.

Вводимые признаки: признаки параллелограмма.

При проведении анализа задачного материала темы определён вид задач и их дидактическая цель. Задачный материал классифицирован по способу задания, характеру требования, способу решения. Результаты анализа представлены в таблице 2.

Результаты анализа задачного материала темы

По способу задания

По характеру требования

По способу решения

По дидактической цели

Задачи представлены математическим текстом

Начертить многоугольник, провести диагонали.

Отработка понятия выпуклого многоугольника и его элементов

Задачи представлены математическим текстом

Найти сумму углов или количество сторон многоугольника

Отработка формулы о сумме углов многоугольника

Задачи представлены математическим текстом

Найти длины сторон четырехугольника

Вспомнить периметр четырехугольни-ка

Задачи представлены математическим текстом

Доказать, что данный четырехугольник-параллелограмм

Применение определения, свойств и признаков параллелограмма

Задачи представлены математическим текстом

Вычислить периметр параллелограмма

Применение определения, свойств и признаков параллелограмма

Задачи представлены математическим текстом

Применение определения, свойств и признаков параллелограмма

Задачи представлены математическим текстом

Доказать свойства и признаки трапеции

Применение определения, трапеции

Задачи представлены математическим текстом

Вычислить стороны или углы трапеции

Применение определения, свойств и признаков трапеции

Задача представлена математическим текстом

Доказать, что из равнобоких трапеций можно сделать паркет

Применение свойств и признаков равнобедренной трапеции

Задачи представлены математическим текстом

Применение определения, свойств и признаков параллелограмма

Задача представлена математическим текстом

Разделить отрезок на части

Применение теоремы Фалеса

Задачи представлены математическим текстом

Применение определения, свойств и признаков трапеции

Задачи представлены математическим текстом

Доказать, что данный четырехугольник является прямоугольником

Применение определения, свойств и признаков прямоугольника

Задачи представлены математическим текстом

Вычислить стороны прямоугольника

Применение определения, свойств и признаков прямоугольника

Задачи представлены математическим текстом

Вычислить стороны или углы ромба

Применение определения, свойств и признаков ромба

Задача представлена математическим текстом

Доказать свойства ромба

Применение определения, свойств и признаков ромба и параллелограмма

Задачи представлены математическим текстом

Доказать, что данный четырехугольник является квадратом

Применение определения, свойств и признаков ромба

Задача представлена математическим текстом

Вычислить периметр квадрата

Применение определения, свойств и признаков квадрата

Задачи представлены математическим текстом

Построить прямоугольник, или ромб, или квадрат

Применение определения, свойств и признаков прямоугольника, ромба и квадрата

Задачи представлены математическим текстом

Распознавать фигуры, обладающие осевой и центральной симметрией

Применение определений осевой и центральной симметрии

Задачи представлены математическим текстом

Доказать, что данная фигура обладает симметрией

Применение определений осевой и центральной симметрии

Задача представлена математическим текстом

Построить фигуру, симметричную данной

Применение определений осевой и центральной симметрии

В результате выполнения анализа задач была проведена их классификация по уровню сложности и виду, на основании которой составлена таблица 3.

Классификация задач по теме «Четырёхугольники»

Логико-дидактический анализ содержания темы «Четырехугольники»

Впервые, в школьном курсе математики, с четырехугольниками школьники встречаются в начальной школе. Изучение четырехугольников, а именно прямоугольника и квадрата, идет поверхностно, как и в 5 и 6 классах.

В учебнике «Геометрия, 7-9», авт. Атанасян Л.С. тема «Четырехугольники» изучается в начале восьмого класса. На изучение данной темы по программе отводится 14 часов .

Тематическое планирование изучения данной темы представлено в таблице 1.

Тематическое планирование, 2 часа в неделю

Характеристика основных видов деятельности ученика

(на уровне учебных действий)

Объяснять , что такое ломаная, многоугольник, его вершины, смежные стороны, диагонали, изображать и показывать многоугольники на чертежах; показывать элементы многоугольника , его внутреннюю и внешнюю области; формулировать определение выпуклого многоугольника ; изображать и распознавать выпуклые и невыпуклые многоугольники; формулировать и доказывать утверждения о сумме углов выпуклого многоугольника и сумме его внешних углов ; объяснять, какие стороны (вершины) четырёхугольника называются противоположными ; формулировать определения параллелограмма, трапеции, равнобедренной и прямоугольной трапеций, прямоугольника, ромба, квадрата; изображать и распознавать эти четырёхугольники; формулировать и доказывать утверждения об их свойствах и признаках ; решать задачи на вычисление, доказательство и построение, связанные с этими видами четырёхугольников ; объяснять , какие две точки называются симметричными относительно прямой (точки), в каком случае фигура называется симметричной относительно прямой(точки) и что такое центр(ось) симметрии фигуры; приводить примеры фигур, обладающих осевой(центральной) симметрией, а также примеры осевой и центральной симметрии в окружающей нас обстановке.

Параллелограмм и трапеция

Прямоугольник. Ромб. Квадрат.

Материал в учебнике по данной теме представлен в V главе «Четырёхугольники», которая содержит три параграфа. Каждый параграф содержит теоретический материал, который разбивается на небольшие смысловые порции, что позволяет ученику лучше осознать и выучить теоретический материал по данной теме. После изучения каждого параграфа идёт система задач различной степени трудности на закрепление изученного материала, а после изученной главы идёт система упражнений и вопросов на отработку знаний, умений и навыков. Дан образец решения задач на доказательство (№378, №384), доказана теорема Фалеса (задача №385), дано решение задач на построение 393 а), 396, даны чертежи ко всем этим задачам.

Названия пунктов выделены другим цветом. Материал для заучивания (понятия, определения, формулировки теорем) выделен жирным тёмным цветом. Имеются рисунки и чертежи для наглядного представления теоретического материала, дано доказательство всех свойств и признаков рассматриваемых фигур.

Изучение четырехугольников в учебнике Л. С. Атанасяна идет по следующей схеме:

Определение. Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.

1˚ В параллелограмме противоположные стороны равны и противоположные углы равны.

2˚ Диагонали параллелограмма точкой пересечения делятся пополам.

1˚ Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.

2˚ Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.

3˚ Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.

Задачи из учебника

371 . Докажите, что выпуклый четырехугольник АВСD является параллелограммом, если: а) ∠ ВАС = ∠ АСD и ∠ ВСА = ∠ DАС;

373. Периметр параллелограмма АВСD равен 50 см, ∠ С=30˚, а перпендикуляр ВН к прямой CD равен 6,5 см. Найдите стороны параллелограмма.

375 . Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см.

376 . Найдите углы параллелограмма АВСD, если: а) ∠ А = 84˚;

б) ∠ А — ∠ В = 55˚; в) ∠ А + ∠ С = 142˚; г) ∠ А=2 ∠ В;

д) ∠ САD=16˚, ∠ АCD = 37˚.

380. На сторонах АВ, ВС, СD и DA четырехугольника АВСD отмечены соответственно точки M, N, P и Q так, что АМ = СР, ВN = DQ, BM = DP, NC = QA. Докажите, что четырехугольник АВСD и MNPQ – параллелограммы.

382. Диагонали параллелограмма АВСD пересекаются в точке О. Докажите, что четырехугольник А1В1С1D1, вершинами которого являются середины отрезков ОА, ОВ, ОС и ОD, — параллелограмм.

№1 . Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC . Найдите AB , если BC = 34.

Решение: По определению параллелограмма ВС || АD, АЕ — секущая при параллельных прямых, следовательно, углы ВЕА и ЕАD равны как накрест лежащие. Поскольку ∠ ВЕА= ∠ ВАЕ, треугольник АВЕ — равнобедренный, откуда АВ=ВЕ. Аналогично, треугольник СЕD —равнобедренный и ЕС=СD. Стороны АВ и СD равны, как противоположные стороны параллелограмма, следовательно:

.

№2. В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что ВFDЕ — параллелограмм.

Решение: Прямоугольные треугольники ABE и CDF равны по гипотенузе и острому углу ( AB = CD как противолежащие стороны параллелограмма; ∠ BAE = ∠ DCF как накрест лежащие углы при параллельных прямых AB и CD и секущей AC ). Следовательно, BE = DF . Кроме того, BE || DF , т. к. это перпендикуляры к одной прямой. Таким образом, в четырёхугольнике BFDE противолежащие стороны равны и параллельны, поэтому BFDE — параллелограмм.

Определение. Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны трапеции называются ее основаниями , а две другие стороны – боковыми сторонами .

Трапеция называется равнобедренной , если ее боковые стороны равны.

Трапеция, один из углов которой прямой, называется прямоугольной .

Задачи из учебника

386. Докажите, что отрезок, соединяющий середины боковых сторон трапеции, параллелен основаниям трапеции.

387. Найдите углы В и D трапеции АВСD с основаниями АD и BC, если ∠А=36˚, ∠С=117˚.

388. Докажите, что в равнобедренной трапеции: а) углы при каждом основании равны; б) диагонали равны.

390. Один из углов равнобедренной трапеции равен 68˚. Найдите остальные углы трапеции.

392. Основания прямоугольной трапеции равны а и b , один из углов равен α. Найдите: а) большую боковую сторону трапеции, если а =4 см, b =7 см, α=60˚; б) меньшую боковую сторону трапеции, если а =10 см , b =15 см, α=45˚.

397. Постройте равнобедренную трапецию АВСD: а) по основанию АD, углу А и боковой стороне АВ; б) по основанию ВС, боковой стороне АВ и диагонали BD.

№1. Прямая, параллельная основаниям трапеции ABCD , пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF , если AD = 44, BC = 24, CF : DF = 3:1

Решение: Проведём построения и введём обозначения как показано на рисунке. Рассмотрим треугольники KFC и ACD, угол C — общий, углы CAD и CKF равны друг другу как соответственные углы при параллельных прямых, следовательно, треугольники KFC и ACD подобны. Откуда поэтому KF= =33. Аналогично, из треугольников EKA и ABC получаем, что EK=BC =24 =6.

Таким образом, EF=EK+KF=6+33=39.

№2. Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F . Найдите AB , если AF = 20, BF = 15.

Решение: Сумма углов, прилежащих к боковой стороне трапеции, равна 180°, значит, .

Получаем, что треугольник ABF прямоугольный с прямым углом F . По теореме Пифагора находим AB : .

Определение. Прямоугольником называется параллелограмм, у которого все углы прямые. Так как прямоугольник является параллелограммом, то он обладает всеми свойствами параллелограмма: в прямоугольнике противоположные стороны равны, а диагонали точкой пересечения делятся пополам.

Особое свойство прямоугольника : Диагонали прямоугольника равны.

Признак прямоугольника: Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.

Задачи из учебника

399. Докажите, что параллелограмм, один из углов которого прямой, является прямоугольником.

401. Найдите периметр прямоугольника АВСD, если биссектриса угла А делит: а) сторону ВС на отрезки 45,6 см и 7,85 см; б) сторону DC на отрезки 2,7 дм и 4,5 дм.

402. Диагонали прямоугольника АВСD пересекаются в точке О. Докажите, что треугольники АОD и АОВ равнобедренные.

403. В прямоугольнике АВСD диагонали пересекаются в точке О. Найдите периметр треугольника АОВ, если =30˚, АС = 12 см.

№1. В параллелограмме ABCD точка E — середина стороны AB . Известно, что EC=ED . Докажите, что данный параллелограмм — прямоугольник.

Решение: Треугольники BEC и AED равны по трём сторонам. Значит, углы CBE и DAE равны. Так как их сумма равна 180°, то углы равны 90°. Такой параллелограмм — прямоугольник.

Определение. Ромбом называется параллелограмм, у которого все стороны равны. Так как ромб является параллелограммом, то он обладает всеми свойствами параллелограмма.

Особое свойство ромба : Диагонали ромба взаимно перпендикулярны и делят

Задачи из учебника

405. В ромбе одна из диагоналей равна стороне. Найдите: а) углы ромба; б) углы, которые диагонали ромба образуют с его сторонами.

406. Найдите периметр ромба АВСD, если =60˚, АС=10,5 см.

402. Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен 45˚.

403. Докажите, что параллелограмм является ромбом, если: а) его диагонали взаимно перпендикулярны; б) диагональ параллелограмма является биссектрисой его угла.

433 . Из вершины В ромба АВСD проведены перпендикуляры ВК и ВМ к прямым AD и DC. Докажите, что луч ВD является биссектрисой угла КВМ.

434. Докажите, что точка пересечения диагоналей ромба равноудалена от его сторон.

№1. Высота AH ромба ABCD делит сторону CD на отрезки DH = 12 и CH = 1. Найдите высоту ромба.

Решение: Поскольку ABCD — ромб, AD = DC = DH + HC = 13.

Треугольник ADH прямоугольный, поэтому: АН=

№2. Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите углы ромба.

В ответе запишите величины различных углов в порядке возрастания без пробелов.

Введём обозначения, как показано на рисунке. Пусть диагональ АС равна 76. Диагонали ромба пересекаются под прямым углом и делятся точкой пересечения пополам. Рассмотрим треугольник АОН, он прямоугольный, найдём синус угла ОАН: sin = , следовательно, угол OAH равен 30°.

Рассмотрим треугольники AOB и AOD, они прямоугольные, AO — общая, AB=AD, следовательно, эти треугольники равны, откуда ∠ ВАO = ∠ OAD=30˚, поэтому ∠ B AD=2∙30˚=60˚. Сумма смежных углов ромба равна 180˚, откуда ∠ AВС=180˚- ∠ B AD=180˚-60˚=120˚.

Определение. Квадратом называется прямоугольник, у которого все стороны равны. Прямоугольник является параллелограммом, поэтому и квадрат является параллелограммом, у которого все стороны равны, т.е. ромбом. Отсюда следует, что квадрат обладает всеми свойствами прямоугольника и ромба.

Основные свойства квадрата :

1. Все углы квадрата прямые.
2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

Задачи из учебника

409. Докажите, что ромб, у которого один угол прямой, является квадратом.

410. Является ли четырехугольник квадратом, если его диагонали: а) равны и взаимно перпендикулярны; б) взаимно перпендикулярны и имеют общую середину; в) равны, взаимно перпендикулярны и имеют общую середину?

411. В прямоугольном треугольнике проведена биссектриса прямого угла. Через точку пересечения этой биссектрисы с гипотенузой проведены прямые, параллельные катетам. Докажите, что полученный четырехугольник – квадрат.

415. Постройте квадрат: а) по стороне; б) по диагонали.

436. Диагональ АС квадрата АВСD равна 18,4 см. Прямая, проходящая через точку А и перпендикулярная к прямой АС, пересекает прямые ВС и СD соответственно в точках М и N. Найдите МN.

№1. Найдите площадь квадрата, описанного вокруг окружности радиуса 39.

Решение: Сторона квадрата равна диаметру вписанной в него окружности, значит площадь данного квадрата равна:

№2 . Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.

Решение: Площадь получившейся фигуры равна разности площадей квадрата и прямоугольника: 6 · 6 − 4 · 2 = 28.

Описанные и вписанные четырехугольники

Описанный четырехугольник — такой, что все его стороны касаются одной окружности. В этом случае окружность вписана в четырехугольник.

В отличие от треугольника не во всякий четырехугольник можно вписать окружность. Например, в прямоугольник, не являющимся квадратом, можно «поместить» окружность, касающуюся трех его сторон, но нельзя вписать окружность.

Если же в четырехугольник можно вписать окружность, то его стороны обладают следующим замечательным свойством:

В любом описанном четырехугольнике суммы противоположных сторон равны. Верно и обратное утверждение.

Вписанный четырехугольник — четырехугольник, все вершины которого лежат на одной окружности. Очевидно, эта окружность будет называться описанной вокруг четырехугольника.

В отличие от треугольника около четырехугольника не всегда можно описать окружность. Например, нельзя описать окружность около ромба, не являющегося квадратом. Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:

В любом вписанном четырехугольнике сумма противоположных углов равна 180˚. Верно и обратное утверждение.

Задачи из учебника

695. Сумма двух противоположных сторон описанного четырехугольника равна 15 см. Найдите периметр этого четырехугольника.

696. Докажите, что если в параллелограмм можно вписать окружность, то этот параллелограмм – ромб.

698. Сумма двух противоположных сторон описанного четырехугольника равна 12 см, а радиус вписанной в него окружности равен 5 см. Найдите площадь четырехугольника.

708. Докажите, что можно описать окружность: а) около любого прямоугольника; б) около любой равнобедренной трапеции.

709. Докажите, что если около параллелограмма можно описать окружность, то этот параллелограмм – прямоугольник.

710. Докажите, что если около трапеции можно описать окружность, то эта трапеция – равнобедренная.

№1. В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S . Найдите NS , если известно, что около четырёхугольника NPQM можно описать окружность, PQ = 14, SQ = 4 .

Решение: Поскольку ∠ QPS = ∠ QPM = ∠ MNQ = ∠ QNP (см. рис.), треугольник PQS подобен треугольнику NQP по двум углам (угол при вершине Q общий). Поэтому . Пусть NS = x . Тогда .

Из этого уравнения находим, что x = 45.

№2. Диагонали четырёхугольника АВСD , вершины которого расположены на окружности, пересекаются в точке М. Известно, что ∠ АВС = 72°, ∠ ВСD = 102°, ∠ AMD = 110°. Найдите ∠ ACD .

Решение : Пусть ∠ АСD = x .

∠ BCA =102˚- x; ∠ DBC+ 102˚- x =70˚; x = ∠ DBC+ 32˚.

∠ DBC+ ∠ ABD =72˚ ; ∠ ABD=x; ∠ DBC =72˚ -x; 2x= 104 ˚; x =52˚.

№3. Два угла вписанного в окружность четырехугольника равны 82˚ и 58˚. Найдите больший из оставшихся углов. Ответ дайте в градусах.

Решение: Сумма противоположных углов вписанного четырехугольника равна 180˚. Пусть угол А равен 82˚. Тогда напротив него лежит угол в 98 градусов. Если угол В равен 58˚, то угол D равен 180˚-58˚=122˚.

№4. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.

Решение: Мы помним, что средняя линия трапеции равна полусумме оснований . Пусть основания трапеции равны a и с, а боковые стороны — b и d. По свойству описанного четырехугольника, a+c=b+d, и значит, периметр равен 2(a+c).
Получаем, что a+c=20, а средняя линия равна 10.

№5. Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 1:2:3. Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 32.

Решение: Пусть сторона АВ равна х , АD равна 2x , а DC — 3x . По свойству описанного четырехугольника, суммы противоположных сторон равны, и значит, х+3х=ВС+2х.
Получается, что BC равна 2х . Тогда периметр четырехугольника равен 8х . Мы получаем, что х= 4, а большая сторона равна 12.

План – конспект урока

на тему «Прямоугольник»

-рассмотреть свойства и признаки прямоугольника как частного случая параллелограмма, сформулировать и доказать его особые свойства и признаки, формировать умения решать задачи с применением доказанных теорем.

-развивать логическое мышление учащихся, умение грамотно выполнять и читать чертежи, математическую речь, интерес к предмету.

-воспитывать дисциплинированность, ответственное отношение к учебному труду.

-Повторить понятия прямоугольника, опираясь на полученные знания в курсе математики 1-6 классе;

-Рассмотреть свойства и признак прямоугольника через элемент исследования;

-Научить обучающихся, применять свойства в процессе решения задач;

-Рассмотреть задачи, развивающие компетентности ученика.

Оборудование: ПК, проектор, экран, презентация.

Тип урока : урок изучения и закрепление новых знаний.

Добрый день ребята!

Я рада видеть вас на нашем уроке. Надеюсь мы с вами сегодня хорошо поработаем.

2. Мотивация урока.

» Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг — геометрия». Эти слова, сказанные великим французским архитектором Ле Корбюзье, в начале ХХ века очень точно характеризуют и наше время. Мир, в котором мы живем, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека. Лучше ориентироваться в нем, открывать новое, понимать красоту и мудрость окружающего мира поможет вам эта наука.

Сегодня на уроке каждый оценит свою работу и выставит себе баллы в оценочный лист.

• правильно выполненное задание – 3 балла

• ошибки при выполнении задания – 2 балла

• невыполнение задания – 0 баллов.

3. Актуализация опорных знаний. Проверка д/з.

Геометрия в 8 классе началась с главы «Четырехугольник». Это одна из важных тем, которая широко используется при решении задач на ОГЭ и ЕГЭ.

Проверка домашнего задания.

— Какая фигура называется четырехугольником?

— Назовите виды четырехугольников, которые изучили?

— Дайте определение трапеции. Какие бывают трапеции. Определение равнобедренной, прямоугольной трапеции.

— Дайте определение параллелограмма.

— Каким свойством обладают противоположные стороны параллелограмма?

— Каким свойством обладают противоположные углы параллелограмма?

— Каким свойством обладают диагонали параллелограмма?

— Сформулируйте признаки равенства прямоугольных треугольников?

Решение задач на готовых чертежах.

4.Изучение нового материала.

В жизни нет важней фигуры!

Прямоугольник всюду есть.

С ним любые процедуры

Угол равен, ему – честь!

Дом и Стол, тетрадь и книжка

Без фигуры этой – крышка!шо

Не построишь – мерь, не мерь!

Запишите число и тему урока.

1.Ввести понятие прямоугольник.

Среди предложенных четырехугольников выбрать те, которые являются прямоугольником.

Давайте будем разбираться с данной фигурой.

Каково взаимное расположение противоположных сторон прямоугольника? Верно, они попарно параллельны.

А мы уже встречались с фигурой, у которой противоположные стороны попарно параллельны, как называется такая фигура? Правильно параллелограмм!

Какой мы можем сделать вывод о прямоугольнике? Как можно назвать прямоугольник? Да. Прямоугольник — это параллелограмм.

А что его отличает от параллелограмма? У него все углы прямые, т. е. равны. А у параллелограмма только противоположные углы равны.

Закончите предложение: «Прямоугольник-это параллелограмм, у которого…….»

2.Рассмотреть особое свойство диагоналей прямоугольника.

Так как прямоугольник – это параллелограмм, то какими свойствами он обладает? Ответим на этот вопрос, исследуйте стороны, углы и диагонали прямоугольника и заполните таблицу на рабочих листах

Каким отличительным свойством он обладает?

Диагонали прямоугольника равны.

1)Рассмотрим Δ ACD и Δ DBA

AB=CD, т. к. ABCD-параллелограмм

2) Значит ΔACD= ΔDBA по 2 катетам.

3) Значит AC=BD, как соотв. элементы в равных треугольниках.

4.Рассмотреть признак треугольника.

Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.

1. AC=BD (по условию), тогда ΔACD = Δ ABD по3 сторонам(AD- общая сторона, AB = CD, AC=BD)
2. ∟A= ∟D — как соответственные элементы

∟A=∟C, ∟B= ∟D, т. к. в параллелограмме противоположные углы равны;

4) ∟A+∟B+ ∟C+ ∟D= 360 0 следовательно,∟A= ∟B= ∟C= ∟D=90 0

5) Значит ABCD- прямоугольник.

Оцените свою работу

5.Закрепление изученного материала

Решение задач на готовых чертежах.

Решение задачи № 403 у доски.

Дано: ABCD – прямоугольник, AC ∩ BD = O, 0 , AC = 12 см.

Оцените свою работу

Впишите пропущенные слова.

Прямоугольником называется _____, у которого все углы _____.

Свойство прямоугольника: _____ прямоугольника равны.

Признак прямоугольника: если в параллелограмме диагонали _____, то этот параллелограмм – _____.

Оцените свою работу

6.Итог урока . Домашнее задание п.45, вопросы 12,13 стр. 115, № 399, № 401 (а).

Мы знаем, что диагонали параллелограмма точкой пересечения длятся пополам.

Применим это свойство для получения оценки за урок. Посчитайте итоговое количество набранных баллов и разделите на 2.

Если вы набрали 10-13 баллов, ваша оценка «5»

Если вы набрали 7-9 баллов, ваша оценка «4»

Если вы набрали 5-7 баллов, ваша оценка «3»

Трудным ли для тебя был материал урока?

На каком из этапов урока было труднее всего, легче всего?

Что нового ты узнал на уроке? Чему научился?

Работал ли ты на уроке в полную меру сил?

Как эмоционально ты чувствовал себя на уроке?

Прием рефлексии «Яблоня»

Яблоня красного цвета : «Я удовлетворен уроком, урок был полезен для меня, я много, с пользой и хорошо работал на уроке, я получил заслуженную оценку, я понимал все, о чем говорилось и что делалось на уроке»

Яблоня желтого цвета : «Урок был интересен, и я принимал в нем активное участие, урок был в определенной степени полезен для меня, я отвечал с места, я сумел выполнить ряд заданий, мне было на уроке достаточно комфортно»

Яблоня зеленого цвета : «Пользы от урока я получил мало, я не очень понимал, о чем идет речь, мне это не очень нужно, домашнее задание я не понял, к ответу на уроке я не был готов»

Исследуйте стороны, углы и диагонали прямоугольника и заполните таблицу на рабочих листах

Впишите пропущенные слова.

Прямоугольником называется ________________, у которого все углы __________.

Свойство прямоугольника: ___________________ прямоугольника равны.

Признак прямоугольника: если в параллелограмме диагонали _________, то этот параллелограмм –_____________.

Критерии оценивание работы

• правильно выполненное задание – 3 балла

• ошибки при выполнении задания – 2 балла

• невыполнение задания – 0 баллов.

Если вы набрали 10-13 баллов, ваша оценка «5»

Если вы набрали 7-9 баллов, ваша оценка «4»

Если вы набрали 5-7 баллов, ваша оценка «3»

Мы находимся в ситуации неопределённости, ситуации постоянного выбора, нас окружает быстро меняющийся мир. В будущем развитие общества будут определять люди умственного труда. Человек, получив профессиональную подготовку, порой вынужден менять профессию или постоянно повышать свою квалификацию. То есть выпускник современной школы должен уметь учиться. Задача учителя дать ученику опыт самостоятельной и исследовательской деятельности.

Главной целью школьного образования является развитие ребёнка как компетентной личности путём включения его в различные виды ценностной человеческой деятельности: учёба, познание, коммуникация, личностное саморазвитие.

В теме «Четырехугольники» закладываются понятия основных видов четырехугольников и здесь же учащиеся знакомятся с основными видами задач, с методами их решения, оформления записи. В ходе изучения важно добиться, чтобы каждый ученик овладел всеми знаниями и умениями, необходимыми для дальнейшего успешного изучения новых понятий и теорем.

Поэтому при подготовке к урокам геометрии по теме «Четырехугольники» учителю необходимо тщательно подбирать учебный материал, наглядные средства. На уроках больше времени отводить самостоятельной работе, творческой деятельности учащихся, использовать различные методики, формы работы. Также учителю необходимо обучать не только готовым знаниям, но и применять в своей работе разнообразные методы познания, приводящие к этим знаниям. Поэтому естественно применять в обучении и те эмпирические методы познания, с помощью которых формулируются гипотезы, подлежащие обоснованию (или опровержению) уже иными методами.

Наблюдение, опыт и измерения должны быть направлены на создание в процессе обучения специальных ситуаций и предоставление учащимся возможности извлечь из них очевидные закономерности, геометрические факты, идеи доказательства и т, д. Все это будет наиболее полно способствовать лучшему усвоению геометрии учениками.

Особое внимание должно уделяться познавательной активности учащихся, их мотивированности к самостоятельной учебной работе. Это предполагает использование нетрадиционных форм уроков, использование компьютерных технологий на уроках, технологии полного усвоения, технологии обучения на основе решения задач, технологии обучения на основе схематических и новых знаковых моделей. Таким образом, цель курсовой работы на тему «Методика изучения четырехугольников в основной школе» выполнена.

Поставленные задачи решены, произведен отбор средств обучения теме, логико–математический анализ темы «Четырехугольники», анализ задачного материала учебника, выполнена классификация задач учебника Геометрия 7-9 Атанасян Л.С., тематическое планирование, разработана таблица задач, методические рекомендации обучения теме и показано их применение при обучении учащихся, проведена классификация четырехугольников, теоретический материал по теме, основные задачи из учебника на данную тему, а также задачи из ОГЭ повышенной сложности с решением. Был разработан план – конспект урока на тему «Прямоугольник».

Для решения поставленных задач были использованы следующие методы исследования : анализ математической и методической литературы по проблеме исследования, учебников и учебных пособий по геометрии; анализ методических рекомендаций из пособия для учителей.

1. Атанасян А. С. Геометрия: учеб. для 7–9 кл. общеобразоват. учреждений / А. С. Атанасян. – М.: Просвещение, 2014. – 335 с.
2. Методика преподавания математики: учебник для вузов / В. А. Оганесян, Ю. М. Колягин [и др.] – М.: Просвещение, 2014. – 368 с.
3. Теоретические основы обучения математике в средней школе: Учебное пособие / Т. А. Иванова, Е. Н. Перевосщикова [и др.] – Н. Новгород: НГПУ, 2013. – 320 с.
4. Изучение геометрии в 7-9 классах. Пособие для учителей. Атанасян Л.С. и др. М.: Просвещение, 2012. — 255 с
5. Примерные программы по математике. – М.:Просвещение, 2014. –67с.
6. Геометрия. Самостоятельные и контрольные работы. 7-9 классы. Иченская М. А. , 2014.
7. Геометрия. Тематические тесты к учебнику Л.С.Атанасяна и др. Авт: Мищенко Т. М., Блинков А. Д. , 2014
8. Геометрия. Рабочая тетрадь. 8 класс. Авт: Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. М.: Просвещение, 2014
9. Геометрия. 7-9 классы. Электронное приложение к учебнику Атанасяна Л.С., Бутузова В.Ф., Кадомцева С.Б./1 CD/
10. Геометрия. Комплект демонстрационных таблиц к учебнику Л.С. Атанасяна с методическими рекомендациями. Авт: Бурмистрова Т. А., Ходот Т. Г., Ходот А. Ю. , 2014
11. Зив Б.Г. Геометрия. Дидактические материалы. 8 класс / Б.Г. Зив, В.М. Мейлер. – М.: Просвещение, 2012.
12. ОГЭ – 2018. Математика. Типовые экзаменационные варианты. 36 вариантов. Авт: Ященко И.В., Кукса Е.А., Лескина О.М.. Изд: Национальное образование, 2018.
13. Фридман Л.М. Психологические основы обучения математике в школе: Учителю математики о педагогической психологии. -М.: Просвещение, 1983

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Проект «Реализация требований ФГОС ООО при обучении учащихся 8 класса по теме «Четырехугольники»»

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

ГБОУ ВПО «Академия социального управления»

Дополнительное профессиональное образование

кафедра математических дисциплин

Реализация требований ФГОС ООО при обучении учащихся 8 класса

слушатель учебного курса

«Актуальные проблемы развития профессиональной компетентности учителя математики (в условиях реализации ФГОС)»

учитель математики МБОУ

Майская СОШ Пушкинского р-на

Романова Лилия Сергеевна

Руководитель курса: кандидат педагогических наук, доцент кафедры математических дисциплин

Фирстова Наталья Игоревна

ГЛАВА 1. Теоретические основы обучения теме «Четырехугольники»

§1. Эссе «Концепция духовно-нравственного развития и воспитания личности гражданина России » ………………………………………….

§2. Логико-дидактический анализ содержания темы «Четырехугольники» ………………………………………………………………….

§3. Цели обучения теме «Четырехугольники» …………………………

ГЛАВА 2. Организация обучения теме «Четырехугольники»

§4. Карта изучения темы «Четырехугольники» и ее использование ….

§5. Учебный план темы «Четырехугольники» …………………………..

§6. Примеры реализации целей обучения теме «Четырехугольники» …

Современный этап развития школьного математического образования характеризуется сменой предметно-ориентированной парадигмы на личностно-ориентированную, что требует адекватной разработки содержательного и процессуального компонентов образования с упором на развитие и саморазвитие учащегося, формирования личностно значимых для него знаний и способов деятельности. В этих условиях формирование только предметных математических знаний недостаточно для становления образованной личности. Наряду с предметными знаниями сегодня нужно формировать умение ориентироваться в потоке новой информации, разрешать возникающие в учебных ситуациях проблемы, отходить от стандартных способов решения задач путем переструктуирования их в соответствии с исходными условиями.

Результаты международных и массовых отечественных исследований уровня математической подготовки учащихся показывают на фоне хорошей теоретической подготовки знаний российских школьников возникновение у них трудностей, а порой полной беспомощности в нестандартных учебных ситуациях, отличающихся от привычных – тех, которые присутствовали в обучении.

Преодоление негативной стороны сложившейся ситуации школьного материала возможно посредством обращения к смысловой стороне математического содержания, к вопросу организации понимающего усвоения математики.

Цель проекта : реализация требований ФГОС ООО при изучении темы «Четырехугольники». Для достижения поставленной цели необходимо решение следующих задач:

1. Выявить теоретические основы обучения теме, связанные с реализацией ФГОС ООО.

2. Провести анализ учебной, методической математической литературы по теме исследования.

3. Провести анализ психолого-педагогической литературы, так как создаю проект для 8 класса ( ученикам 13-14 лет)

4. Выполнить логико-дидактический анализ по выбранной теме.

5. Разработать тематическое планирование, таблицу целей и карту обучения теме с учетом ФГОС.

6. Разработать фрагменты конспектов уроков по выбранной теме.

7. Выполнить отбор средств обучения теме, в том числе средства ИКТ.

Решение поставленных задач потребовало использования следующих методов исследования: изучение «Концепции духовно-нравственного развития и воспитания личности гражданина России»; анализ психолого-педагогической, математической и методической литературы по проблеме исследования, учебников и учебных пособий по математике; беседы с учителями, тестирование учащихся, проведение опытной проверки.

На наш взгляд, когда тема будет таким образом разработана, ученики лучше усвоят эту тему.

Изучение математики в основной школе направлено на достижение следующих целей:

развитие логического и критического мышления, культуры речи;

формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;

овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни.

Цель содержания раздела «Геометрия» развить у учащихся пространственное воображение и логическое мышление путем систематического изучения свойств геометрических фигур на плоскости и в пространстве и применения этих свойств при решении задач вычислительного и конструктивного характера.

Тема «Четырехугольники» имеет важное значение для всего курса математики, так как в ней рассматриваются свойства и признаки четырехугольников. Изучение сопровождается решением большого количества задач, поэтому при изучении данной продолжается развитие пространственных представлений учащихся, конструктивных навыков изображения фигур на плоскости, навыков выполнения рисунков, их правильного восприятия и чтения. Использование в задачах в многогранниках (призмы и пирамиды) позволяет подготовить учащихся к изучению соответствующего раздела в курсе стереометрии.

ГЛАВА 1. Теоретические основы обучения теме «Четырехугольники»

§1. Эссе «Концепция духовно-нравственного развития и воспитания личности гражданина России »

Считаем, что в настоящее время духовно-нравственное воспитание особенно актуально, так как в современной жизни низкий уровень общественной морали, утрачиваются семейные ценности, патриотические чувства, среди подростков процветает курение, наркомания. Поэтому на духовно-нравственное воспитание надо уделять большое внимание не только в воспитательной работе, но и на каждом уроке, в том числе и математике. Духовно-нравственное воспитание формирует у человека:
— нравственные чувства (совесть, долг, ответственность, гражданственность, патриотизм);
— нравственный облик (терпение, милосердие, кротость, незлобивость);
— нравственную позицию (способность к различению добра и зла, проявление самоотверженной любви, готовность к преодолению жизненных испытаний)

— нравственное здоровье (создание условий для сохранения физического, психического здоровья,

— воспитание негативного отношения к вредным привычкам, пропаганда физической культуры и здорового образа жизни);
— нравственное поведение (готовность служения людям и Отечеству, проявление духовной рассудительности, послушания, доброй воли).

Учитель должен помнить, что встречаясь даже с очень одаренным учеником, он готовит из него не математика, а прежде всего всесторонне развитую личность, и эту работу он выполняет в тесном единстве с учителями других школьных дисциплин. Обучение математике призвано содействовать выработке представлений о предмете математики, ее сущности и специфике её метода, расширению и обогащению жизненного опыта человека. Воспитательная функция математики осуществляется не столько благодаря её содержанию, сколько за счет использования связанного с этим содержанием обширного материала, который расширяет жизненный опыт, формирует мировоззрение и убеждения учащихся.

Мы считаем, что математика обладает большим воспитательным потенциалом. Реализация воспитательного потенциала урока математики возможна через отбор содержания материала, через структуру урока, организацию общения .

Ни один школьный предмет не может конкурировать с возможностями математики в воспитании мыслящей личности. Даже выполнение скучных и рутинных преобразований опосредованно способствует выработке таких качеств, как собранность и систематичность.

Математика учит строить и оптимизировать деятельность, вырабатывать и принимать решения, проверять действия, исправлять ошибки, различать аргументированные и бездоказательные утверждения, Решение задач требует от учащихся добросовестной и серьезной работы над приобретением и укреплением знаний, что приводит к систематическому напряжению умственных усилий, настойчивости в преодолении трудностей. При этом у учащегося воспитываются такие черты характера как трудолюбие, усидчивость, упорство в преследовании намеченной цели, умение не останавливаться перед трудностями и не впадать в уныние при неудачах.

Перед современным обучением математике поставлен комплекс взаимосвязанных целей – образовательных, развивающих, воспитательных. Обучение математике требует от школьников умственных и волевых усилий, развитого внимания и отточенного логического мышления, воспитание таких качеств, как активность, творческая инициатива, умений коллективного учебно-познавательного труда.

Заканчивая, хочется обратиться к словам замечательного С.Л. Соловейчика, который в своей книге «Педагогика для всех» говорит: «Воспитание — это обучение нравственной жизни, т.е. обучение нравственным средствам. Воспитывая детей, мы учим их добиваться своих целей за свой счет — пользуясь лишь нравственными средствами. Нравственность (определяемая вопросом «за чей счет?») указывает нижнюю границу возможных для человека действий и поступков; через требования нравственности переступить невозможно. Нравственность — граница дозволяемого совестью. А верхней границы нет, вверх — духовность, она бесконечна. Будет нравственность, почти наверняка будет и духовность; не будет нравственности – не будет ничего, никакого воспитания». [16]

§2. Логико-дидактический анализ темы «Четырехугольники»

Хоть я не особенно забочусь о славе, однако параллелограммом горжусь больше, чем каким-либо другим изобретением, сделанным мною.

(английский изобретатель, 1736-1819)

Основная цель изучения темы «Четырехугольники» — изучить наиболее важные виды четырехугольников — параллелограмм, прямоугольник, ромб, квадрат, трапецию; дать представление о фигурах, обладающих осевой или центральной симметрией. Осевая и центральная симметрии вводятся не как преобразование плоскости, а как свойства геометрических фигур, в частности четырехугольников.

В древних египетских и вавилонских математических документах встречаются следующие виды четырехугольников: квадраты, прямоугольники, равнобедренные и прямоугольные трапеции. В частности, в клинописных математических табличках встречаются прямоугольные треугольники, рассеченные параллелями к одному из катетов на прямоугольные трапеции

Термин «параллелограмм» — греческого происхождения и, согласно Проклу, был введен Евклидом. Понятие параллелограмма и некоторые его свойства были известны еще пифагорейцами.

В «Началах» Евклида доказывается следующая теорема: в параллелограмме противоположные стороны равны и противоположные углы равны, а диагональ разделяет его пополам. Евклид не упоминает о том, что точка пересечения диагоналей параллелограмма делит их пополам. Он не рассматривает ни прямоугольника, ни ромба

Термин «диагональ» происходит от сочетания двух греческих слов «диа» (через) и «гониос» (угол), то есть прямая, проходящая через вершины углов. Однако Евклид и большинство древнегреческих математиков пользовались почти всюду, в частности для прямоугольника, не этим, а другим термином: диаметр. В средние века были в ходу оба термина. Фибоначчи и Региомонтан еще пользовались термином «диаметр». Лишь в XVIII в. термин «диагональ» входит в общее употребление.

Слово «ромб» тоже греческого происхождения, оно означало в древности вращающееся тело, веретено, юлу. Образ ромба был связан первоначально с сечением, проведенным в обмотанном веретене.

Термин «квадрат» происходит от латинского quadratum ( quadrare – сделать четырехугольным), перевод с греческого «тетрагонон» — четырехугольник.

Трапеция – слово греческое означавшее в древности «столик». В «Началах» термин «трапеция» применяется не в современном, а в другом смысле: любой четырехугольник (не параллелограмм).

Предложение о том, что средняя линия трапеции равна полусумме ее оснований, было известно древним египтянам, оно содержится в папирусе Ахмеса и фигурирует в виде инскрипции (II в. до н. э.) на стенах Эдфу в верхнем Египте. Это предложение было известно также вавилонским землемерам, оно содержится и в трудах Герона Александрийского. [3]

Изучение этой темы необходимо для изучения смежных дисциплин: в физике применяют параллелограмм при изучении разложения сил, при нахождении равнодействующей силы; в стереометрии при изучении призмы, четырехугольной пирамиды, в черчении.

С помощью снимка галактики Certaurus А, сделанным инфракрасным космическим телескопом Spitzer , впервые удалось определить структуру пылевого облака галактики. Оказалось, что оно имеет форму параллелограмма

За счёт трёхмерной оптической иллюзии в комнате Эймса (придумал в 1946 году) ребёнок в ближнем углу кажется великаном по сравнению с тем, что стоит в дальнем. На самом деле форма комнаты – трапеция. Эффект усиливается из-за искажённой шахматной клетки .

Символы индейцев Северной Америки

Квадрат выражает постоянство, стойкость и надежность. Он дает защиту. Все стоит на стабильной основе.

Ромб символизирует защитную силу ветра. Он изображает четыре фазы учения, показывает, что смысл жизни в равенстве, единстве и в свободе от страхов.

Прямоугольник указывает на концентрацию на чем-то одном. Применительно к человеку знак сообщает, что тот работает или действует лучше всего в одиночку.

Параллелограмм олицетворяет благодарность, способность учиться и принимать новые идеи.

Свойство подвижности параллелограмма часто используется на практике. Так, шарнирный параллелограмм применяется, например, для проведения параллельных прямых на различных расстояниях друг от друга.

Ромб, в котором проведены диагонали, считается одной из самых крепких и

выносливых конструкций. Такую конструкцию очень широко используют для постройки мостов, зданий, и даже, для рамы мотоцикла.

Ученики с некоторыми понятиями были ознакомлены ранее в начальной школе и в 5 классе, но определения не вводились.

Тема «четырехугольники» изучается в начале восьмого класса. На её изучение отводится целая глава. Первый параграф данной главы посвящен многоугольникам. Дается определение многоугольника (п. 39), а также что называют вершинами и сторонами многоугольника. Говорится, что называется n-угольником. Приводятся примеры фигур, которые являются многоугольниками и тех, которые не являются многоугольниками. Дается определение соседних вершин и диагоналей многоугольника. В конце данного пункта говорит о том, что любой многоугольник разделяет плоскость на две части (внутренняя и внешняя область многоугольника).
В следующем пункте первого параграфа (п. 40) рассказывается о выпуклых многоугольниках. Приводится пример выпуклого и невыпуклого многоугольника. Рассматривая выпуклый n-угольником A ₁ A ₂ A ₃ …An- ₁ An говорится, что углы AnA ₁ A ₂ , A ₁ A ₂ A ₃ , …, An- ₁ AnA ₁ называются углами этого многоугольника и показывает чему равняется сумма углов выпуклого n-угольника.
Последний пункт данного параграфа (п. 41) посвящен четырехугольнику. Определение четырехугольника не дается, просто говорится, что четырехугольник имеет четыре вершины, четыре стороны и две диагонали. Дается определение противоположных сторон и вершин. Приводится пример выпуклого и невыпуклого четырехугольника. На основании суммы углов выпуклого n-угольника делается вывод, что сумма углов выпуклого четырехугольника равна 360°.
Второй параграф посвящен параллелограмму и трапеции. При изучении параллелограмма (п. 42) дается его определение, и доказываются его свойства.

В следующем пункте параграфа (п. 43) рассказывается о признаках параллелограмма. Рассматривается три признака параллелограмма. Это позволяет быстрее решать задачи на доказательство.
Последний пункт параграфа (п. 44) отводится трапеции. В этом пункте дается определение трапеции и рассматриваются виды трапеции. В этом учебнике также предлагается для изучения теорема Фалеса, но в явном виде она не выделена отдельным пунктом.

Третий параграф посвящен прямоугольнику, ромбу и квадрату. Определение прямоугольника и ромба даются на основе параллелограмма. Так как прямоугольник и ромб являются параллелограммом, то они обладают всеми свойствами параллелограмма. Также в учебнике рассматривается особые свойства прямоугольника и ромба. Определение квадрата дается на основе прямоугольника. Так же говорится, что квадрат является ромбом, так как стороны квадрата равны. На основе этого делается вывод, что квадрат обладает свойствами прямоугольника и ромба, добавляются особые свойства квадрата.
В конце параграфа отдельным пунктом (п. 47) выделена осевая и центральная симметрия. В конце главы предлагаются задачи на отработку ЗУН.
Изучение четырехугольников в учебнике Л. С. Атанасяна идет по следующей схеме:

Параллелограмм → Трапеция → Прямоугольник → Ромб → Квадрат

В учебнике четырехугольник вводится как частный вид многоугольника.

📽️ Видео

Классификация четырёхугольников (видео 58) | Подобие. Геометрия | МатематикаСкачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

Описанные четырехугольники. 9 класс.Скачать

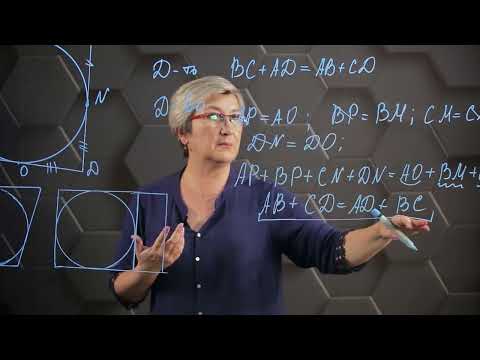
Классификация четырехугольников.Скачать

Виды четырёхугольниковСкачать

Четырехугольники. Вебинар | МатематикаСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Гармония четырехугольников (feat. МО из Школково)Скачать

Геометрия 8. Урок 4 - Прямоугольник, ромб, квадрат - свойства и признаки.Скачать

Четырехугольники | ФормулыСкачать

ЧЕТЫРЕХУГОЛЬНИКИ. ВИДЫ И СВОЙСТВА ЧЕТЫРЕХУГОЛЬНИКОВ. Часть 1Скачать

ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

ГЕОМЕТРИЯ 8 класс: Четырехугольники | Видеоурок с теорией и решением задачиСкачать

Описанная и вписанная окружности четырехугольника - 8 класс геометрияСкачать