Формула герона для четырехугольника

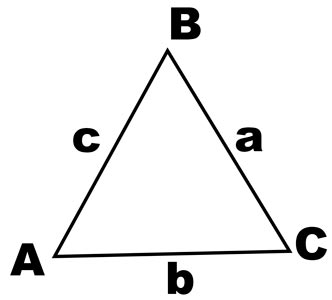
Эта формула позволяет вычислить площадь S треугольника по его сторонам a, b и с:

где р — полупериметр треугольника, т.е. р = (а + b + c)/2. Формула названа в честь древнегреческого математика Герона Александрийского (около I в.). Герон рассматривал треугольники с целочисленными сторонами, площади которых также являются целыми числами. Такие треугольники называют героновыми. Например, это треугольники со сторонами 13, 14, 15 или 51, 52, 53.

Вывод формулы Герона для площади треугольника

Одним из способов позволяющим вывести формулу Герона является использование свойств вписанной в треугольник окружности. Это свойство позволяет вычислить радиус вписанной в треугольник окружности через длины сторон треугольника и полупериметр треугольника.

Предположим у нас есть произвольный треугольник с вершинами А,В и С сторонами длины которых равны а, b и с.

Впишем в этот треугольник окружность.

Из центра этой окружности опустим перпендикуляры к каждой из сторон треугольника и обозначим длину каждого из перпендикуляров буквой r.

Теперь из каждой вершины треугольника проведем к центру окружности три отрезка.

В результате мы видим, что наш треугольник АВС состоит из трех малых треугольников: АОС, АОВ, ВОС

Следовательно, площадь треугольника АВС мы можем вычислить суммированием площадей малых треугольников, т.е.

Далее, площадь треугольника можно найти, также используя формулу S = а*h/2 (2), где а – длина основания треугольника; h – высота треугольника (в нашем случае она равно r).

Теперь запишем формулу (1) выразив площади малых треугольников через формулу (2), т.е.

Давайте упрости формулу (3) вынеся высоту треугольника r и знаменатель каждого из слагаемых за скобки. В итоге мы получим следующую формулу

Часть выражения справа, а именно (а + b + c)/2 есть не что иное, как периметр треугольника, деленный пополам или говоря просто полупериметр треугольника. Обозначим полупериметр треугольника малой буквой р.

В результате формулу (4) мы можем записать в виде

Как уже говорилось выше, радиус вписанной в треугольник окружности можно выразить через длины сторон треугольника и его полупериметр. Формула для радиуса вписанной в треугольник окружности будет выглядеть следующим образом:

Теперь давайте запишем формулу (5) выразив радиус через длины сторон треугольника и его полупериметр,

И после того как перед коренное значение мы заведем под корень, мы получим окончательную формулу

Как мы видим формула (8) есть не что иное, как хорошо известная с античных времен формула Герона.

Формула Герона для площади четырехугольников

Существуют аналоги формулы Герона для четырехугольников. В связи с тем что задача на построение четырехугольника по его сторонам а, b, с и d имеет не единственное решение, для вычисления в общем случае площади четырехугольника недостаточно только знания длин сторон. Приходится вводить дополнительные параметры или накладывать ограничения. Например, площадь вписанного четырехугольника находится по формуле:

Если же четырехугольник и вписанный, и описанный одновременно, его площадь находится по более простой формуле:

Видео:Формула ГЕРОНАСкачать

Площадь четырехугольника

Площадь произвольного четырехугольника, формулы и калькулятор для вычисления в режиме онлайн. Для вычисления площади произвольного четырехугольника применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь произвольного четырехугольника или проверить уже выполненные вычисления.

В окончании статьи приведены ссылки для вычисления частных случаев четырехугольников: квадрата, трапеции, параллелограмма, прямоугольника, ромба.

Видео:8 класс, 18 урок, Формула ГеронаСкачать

Площадь четырехугольника по диагоналям и углу между ними

Видео:найти площадь треугольника. Формула Герона. Известны 3 стороны.Скачать

Площадь четырехугольника через стороны и углы между этими сторонами

При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:

Видео:Запомни: все формулы для площади треугольникаСкачать

Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты

Данная формула справедлива только для четырехугольников, вокруг которых можно описать окружность.

При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:

Видео:Формула Брахмагупты. Площадь вписанного четырехугольника.Скачать

Площадь четырехугольника в который можно вписать окружность

Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.

При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:

Видео:Геометрия 8. Урок 12 - Площадь четырехугольников. Формулы.Скачать

Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними

Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.

Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°

Видео:57. Формула ГеронаСкачать

Таблица с формулами площади четырехугольника

исходные данные (активная ссылка для перехода к калькулятору)	эскиз	формула
1	диагональ и угол между ними
2	стороны и углы между этими сторонами
3	стороны (по Формуле Брахмагупты)
4	стороны и радиус вписанной окружности
5	стороны и углы между ними

Видео:Геометрия 8 класс (Урок№13 - Формула Герона.)Скачать

Площадь частных случаев четырехугольников

Для вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта:

Определения

Четырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками.

Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.

Площадь четырехугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками.

Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т.д.

Видео:Формула Герона. Урок 10. Геометрия 8 классСкачать

Формулы площадей всех фигур в геометрии — примеры вычислений

Площадь — это одна из наиболее важных и неотъемлемых характеристик любой замкнутой геометрической фигуры, показывающая её размер. Она может измеряться в различных единицах: квадратных миллиметрах, сантиметрах, дециметрах, метрах и так далее. Это своеобразный аналог объёма трёхмерных фигур (шара, цилиндра, конуса и других). В геометрии разработаны формулы площадей. Их доказательством являются соответствующие теоремы. Существует общепринятое обозначение площади — буква S (от англ. square).

Видео:Формула Герона.Скачать

Формулы для треугольников

Имеется несколько формул площади треугольника. Если в треугольнике известны две величины: во-первых, длина стороны, а во-вторых, высота, опущенная из противоположного угла перпендикулярно этой стороне, то площадь можно определить, умножив длину на высоту и разделив полученное произведение на два. Выглядит формула так: S = ½ * a * h. Буквой a обозначена длина, буквой h — высота.

При известности всех трёх сторон — a, b, c, широко применяется формула, названная в честь Герона — математика из Древней Греции: S = √(p*(p — a)*(p — b)*(p — c)). Величина p — это половина от периметра треугольника (полупериметр). Чтобы его рассчитать, необходимо суммировать все стороны и разделить сумму на два: (a + b + c)/2.

Для ещё одной формулы требуются следующие данные:

• длина двух соприкасающихся в одной вершине сторон — a и b;
• градус угла, который образуют эти стороны.

Тогда расчёт можно произвести таким способом: S = ½ * a * b * sin γ. Синус угла является одной из тригонометрических функций, представляющей собой результат деления (отношение) в прямоугольном треугольнике противолежащего (дальнего) катета к гипотенузе (сторона напротив прямого угла). Значение sin γ для конкретного угла можно посмотреть в специальной таблице.

Когда два треугольника являются подобными (подобие означает, что у них равны углы и стороны пропорциональны), то отношение их площадей соответствует отношению возведённых в квадрат сторон. Такое отношение сторон для них (например, AB: A (1) B (1)) именуется коэффициентом подобия (k). Поэтому отношение площадей равняется коэффициенту подобия в квадрате.

Если в треугольнике даны все стороны, тогда, кроме формулы Герона, есть возможность воспользоваться ещё одним способом. Он основан на том, что можно вписать любой треугольник в круг. Зная такую величину, радиус ® окружности и три стороны треугольника, производится расчёт: S = (a * b * c) / 4 R.

В любой треугольник: равносторонний и разносторонний, остроугольный и тупоугольный, в силу его геометрических свойств также может быть вписана окружность. В таком случае формула нахождения площади следующая: S = p * r. Буква p обозначает ½ периметра треугольника, r — это радиус окружности.

Видео:Задачи на формулу Герона. Угол и высота по трём сторонам треугольника. Геометрия 8-9 классСкачать

Площадь четырёхугольников

Четырёхугольник — это одна из фигур в геометрии (многоугольник), имеющая четыре стороны, а также четыре вершины, три из которых не находятся на одной прямой. Четырёхугольник называется выпуклым, если он располагается по одну сторону относительно прямой, являющейся продолжением любой из его сторон.

К выпуклым четырёхугольникам относятся практически все известные фигуры, имеющие четыре вершины, а также четыре стороны. Основными их видами выступают: 1) ромб; 2) прямоугольник; 3) трапеция; 4) квадрат; 5) параллелограмм.

Квадрат и прямоугольник

Самый простой способ вычисления площади квадрата — умножить сторону «саму на себя», иными словами, возвести в квадрат длину любой из его сторон (S = a 2 ). Такой расчёт обусловлен особым признаком квадрата — тем, что все его стороны являются абсолютно равными между собой, поэтому квадрат называется правильной фигурой.

Существует вторая, более сложная, формула площади квадрата, где осуществляется расчёт через диагональ. Диагональ — это линия, соединяющая в фигуре два угла, друг другу противоположных. Для определения площади необходимо длину диагонали возвести в квадрат и полученный результат разделить на два: S = ½ d 2 .

Для прямоугольника используется формула: S = a * b, где a, b — длина двух разных, имеющих общую вершину, сторон.

Параллелограмм, ромб и трапеция

Параллелограмм представляет собой четырёхугольник, в котором имеются два противоположных друг другу тупых угла и два — острых.

Применяются три формулы площади параллелограмма:

• Умножить сторону на высоту, перпендикулярную стороне: S = a * h.
• Перемножить две, выходящих из одной вершины, стороны параллелограмма, и умножить на синус угла, образованного ими: S = a * b * sin γ.
• Перемножить диагонали фигуры, затем умножить на синус угла, образованного диагоналями, и разделить результат на два: S = ½ d (1) * d (2) * sin γ.

Ромб похож на параллелограмм с одним отличием: он является равносторонним. Поэтому для вычисления площади ромба используются похожие формулы:

Площадь ромба рассчитать можно также, перемножив диагонали и разделив полученное число на два: S = ½ d (1) * d (2).

Трапеция является геометрической фигурой, имеющей такие элементы: два параллельных основания — верхнее и нижнее, две боковые стороны, расположенные к нижнему основанию под острым углом. Что касается боковых сторон, то они могут быть как равными по длине (так называемая равнобедренная трапеция), так и разными.

В связи с тем, что в «составе» трапеции можно «выделить» прямоугольник и два расположенных по бокам от него треугольника, то можно определить площадь по специальной формуле Герона: S = (a + b): | a + b | * √(p — a) * (p — b) * (p — a — c) * (p — a — d).

В этой формуле имеются следующие обозначения:

• буквы a, b — это основы трапеции,
• буквы c, d — стороны,
• p — полупериметр.

Выпуклый четырёхугольник

В отношении всех иных выпуклых четырёхугольников, то есть имеющих разные по длине стороны и разные углы, разработаны свои формулы вычисления площади.

Прежде всего, можно перемножить две диагонали, а также синус образуемого ими угла, разделив общий результат на два, то есть применить формулу: S = ½ d (1) * d (2) * sin γ.

В том случае, когда внутри выпуклого четырёхугольника, так же как и внутри треугольника, может быть вписан круг, то для нахождения площади четырёхугольной фигуры, требуется определить две величины:

• r — радиус окружности;
• p — ½ периметра четырёхугольника.

После чего полупериметр умножается на радиус. Это и будет площадь четырёхугольника. Формула выглядит так: S = p * r.

Для тех случаев, когда круг может быть очерчен вокруг четырёхугольника, применяется другая формула. Для её использования все стороны фигуры должны быть известны. Они обозначаются буквами a, b, c, d. Рассчитывается половина периметра: p = (a + b + c + d)/2. Затем определяется площадь: S = √(p — a)(p — b)(p — c)(p — d).

Когда конфигурация четырёхугольника такова, что не позволяет возле него описать круг, то в связи с этим формула площади немного дополняется: S = √(p — a)(p — b)(p — c)(p — d) — abcd cos 2 γ.

Коэффициент γ представляет собой половину от суммы двух противоположных углов четырёхугольной фигуры: γ = (угол (1) + угол (2)) / 2.

Видео:Как вывести формулу Герона?Скачать

Круг и эллипс

Самое распространённое и широко применяемое правило определения площади круга — это умножение радиуса окружности в квадрате на число пи: S = π * r 2 .

Число пи, обозначаемое греческой буквой «π» — это математическая постоянная, которая является результатом деления длины окружности на диаметр. π — иррациональное число. Для расчётов признаётся его среднее значение, равное 3,14.

Вместо радиуса можно использовать диаметр окружности: диаметр возводится в квадрат, умножается на число π, результат делится на четыре. Формула выглядит так: S = (π * d 2 ) / 4.

Для того чтобы посчитать площадь такой фигуры, как эллипс, необходимо провести две оси, то есть две линии, каждая из которых разделяет эллипс на две равные части, при этом сами линии перпендикулярны друг другу (образуют прямой угол). Точка пересечения разделяет каждую из осей напополам, образуя полуоси.

Площадь эллипса вычисляется как произведение трёх величин: числа π, длины большой полуоси (а) и длины малой полуоси (b): S = π * a * b. Для удобства расчёта площадей различных фигур также можно использовать специальные онлайн-калькуляторы.

🎥 Видео

Геометрия Как найти площадь четырехугольника, если нет формулыСкачать

Откуда взялся Герон? Формула Герона | Ботай cо мной #028 | Борис Трушин |Скачать

Площадь четырёхугольника через диагоналиСкачать

Площади фигур. Сохраняй и запоминай!#shortsСкачать

Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

От вас это скрывают! Простейшее доказательство формулы Герона и Брахмагупты из Сталинского учебникаСкачать

Геометрическое доказательство формулы Герона | Ботай со мной #052| Борис Трушин |Скачать

КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать