Рассмотрим на конкретных примерах, как найти площадь четырёхугольника, вписанного в окружность.
1) В окружность вписан четырёхугольник, стороны которого последовательно равны 3 см, 5 см, 8 см и 10 см. Найти площадь четырёхугольника.

По формуле Брахмагупты:
где p — полупериметр четырёхугольника, то есть

Проведём диагональ AC.
По теореме косинусов из треугольников ABC н ADC найдём AC², приравняем правые части и получим косинус угла ABC:
Затем найдём синус угла ABC
найдём площади треугольников ABC и ADC:
2) В окружность вписан четырёхугольник, стороны которого последовательно равны 7 см, 24 см, 20 см, 15 см. Найти площадь четырёхугольника.
следовательно, ∠ABC=90º, треугольники ABC и ADC — прямоугольные.
то AB и BC, а также AD и CD — катеты прямоугольных треугольников с общей гипотенузой AC).
Таким образом, для частного случая можно сделать вывод: если для вписанного четырёхугольника, стороны которого последовательно равны a, b, c и d, выполняется условие
то площадь четырёхугольника можно найти по формуле
- В окружность радиуса R вписан правильный четырехугольник?
- Найдите радиусы вписанной и описанной окружностей для правильного треугольника четырехугольника шестиугольника?
- Радиус окружности равен 6?
- Радиус окружности , описанной около правильного четырехугольника , равен 8 см ?
- 1. Радиус вписанного в треугольник окружности = r, найдите сторону треугольника 2?
- В правильный шестиугольник вписана окружность радиуса r?
- Радиус окружности равен 10см ?
- В окружность вписан правильный четырехугольник, и вокруг этой окружности описан правильный четырехугольник?
- В окружность вписан правильный восьмиугольник?
- Найдите площадь правильного шестиугольника, вписанного в окружность радиуса 8 см?
- Найдите площадь правильного 12 — тиугольника, вписанного в окружность радиуса 9?
- Площади четырехугольников
- Формулы для площадей четырехугольников
- Вывод формул для площадей четырехугольников
- 📸 Видео
Видео:Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

В окружность радиуса R вписан правильный четырехугольник?
Геометрия | 5 — 9 классы
В окружность радиуса R вписан правильный четырехугольник.
Найдите его площадь.
Правильный четырехугольник — это квадрат, значит в окружность вписан квадрат.
Диагональ квадрата является диаметром окружности.
Диагонали квадрата пересекаются пол прямым углом и делят квадрат на 4 равных прямоугольных треугольника, катеты которых раны радиусу описанной около квадрата окружности, т.
Тогда площадь квадрата равна площади 4 треугольников.
S = 4 * 1 / 2 * R * R = 2$R^$.
Видео:Задание № 1087 — Геометрия 9 класс (Атанасян)Скачать

Найдите радиусы вписанной и описанной окружностей для правильного треугольника четырехугольника шестиугольника?
Найдите радиусы вписанной и описанной окружностей для правильного треугольника четырехугольника шестиугольника.
Пожалуйста нужно срочно.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Радиус окружности равен 6?
Радиус окружности равен 6.
Найдите площадь правильного треугольника, вписанного в эту окружность.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Радиус окружности , описанной около правильного четырехугольника , равен 8 см ?
Радиус окружности , описанной около правильного четырехугольника , равен 8 см .
Найдите отношение периметра данного четырехугольника к длине вписанной окружности.
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

1. Радиус вписанного в треугольник окружности = r, найдите сторону треугольника 2?
1. Радиус вписанного в треугольник окружности = r, найдите сторону треугольника 2.
Радиус вписанный в правильный четырехугольник = r найдите сторону четырехугольника.
Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать

В правильный шестиугольник вписана окружность радиуса r?
В правильный шестиугольник вписана окружность радиуса r.
Найдите площадь шестиугольника.
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Радиус окружности равен 10см ?
Радиус окружности равен 10см .
Найдите стороны вписанного в окружность правильного треугольника , правильного четырехугольника , правильного шестиугольника .
Пожалуйста с решениеи .
Видео:Площадь круга. Математика 6 класс.Скачать

В окружность вписан правильный четырехугольник, и вокруг этой окружности описан правильный четырехугольник?
В окружность вписан правильный четырехугольник, и вокруг этой окружности описан правильный четырехугольник.
Найдите отношения периметров и площадей этих четырехугольников.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

В окружность вписан правильный восьмиугольник?
В окружность вписан правильный восьмиугольник.
Сумма длин всех его диагоналей, имеющих наименьшую длину, равна 8.
Найдите площадь правильного четырехугольника, вписанного в эту же окружность.
Видео:ОГЭ Площадь квадрата, описанного около окружности #огэ #огэ2023 #алгебра #огэматематикаСкачать

Найдите площадь правильного шестиугольника, вписанного в окружность радиуса 8 см?
Найдите площадь правильного шестиугольника, вписанного в окружность радиуса 8 см.
Видео:Задание № 1088 — Геометрия 9 класс (Атанасян)Скачать

Найдите площадь правильного 12 — тиугольника, вписанного в окружность радиуса 9?
Найдите площадь правильного 12 — тиугольника, вписанного в окружность радиуса 9.
Вопрос В окружность радиуса R вписан правильный четырехугольник?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 5 — 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.
Второй угол — 126 градусов. Угол будет равен 126 делим на 2 = 63 градуса.
Задание № 6 : В прямоугольный треугольник ABC с прямым углом A и катетами AB = 2, AC = 6 вписан квадрат ADEF. Найдите отношение площади треугольника EFC к площади квадрата ADEF. РЕШЕНИЕ : Пусть сторона квадрата х. Тогда FC = (6 — x). Площадь треу..
Sб = 2ПtH (h вторая сторона. Её нужно узнать) Подставляем : 100 = 2 * 5 * П * H H = 100 / 2 * 5П H = 100 / 10 H = 10 S(прямоугольника) = 10 * 5 = 50см ^ 2 Вроде так)).
Визначимо периметр в частинах 2( 9 + 5 ) = 28 Це і є 112 см по довжині. Тепер 112 : 28 = 4 см — довжина однієї частини. Визначаємо довжину сторін : 4 х 9 = 36 см Друга сторона 4 х 5 = 20 см Тепер перевірка за периметром : 36 + 36 + 20 + 20 = 112 см..
Правильная пирамида — это пирамида, основанием которой является правильный многоугольник, а вершина пирамиды проецируется в центр этого многоугольника. Диагонали, проведенные через центр основания данной пирамиды, делят его на 6 правильных треугольн..
По теореме Пифагора : С2 = а2 + б2 Б2 = (2√2)2 — (√5) Б2 = 8 — 5 = Б = √3.
ВН ^ 2 = 52 ^ 2 — 10 ^ 2 = 2704 — 400 = 42304 ВН = 48 S = (АН + НD) * ВН = 22 * 48 = 1056.
Угол АЛС 60 градусов.
Сторони паралелограм можна вважати поділенимина 6 рівних частин. Отже, 42 : 6 = 7 см — менша сторона, 7 * 2 = 14 см більша сторона. Відповідь : 7 см і 14 см.
Сумма углов треугольников равна 180 градусов. Разделим в соответствии с заданной пропорцией. 1 часть равна 180 / (1 + 2 + 3) = 180 / 6 = 30 градусов. Угол А равен 30 градусов. Угол В равен 30 * 2 = 60 градусов. Угол С равен 30 * 3 = 90градусов. ..
Видео:Нахождение радиуса описанной окружности около правильного четырехугольникаСкачать

Площади четырехугольников
 Формулы для площадей четырехугольников Формулы для площадей четырехугольников |
 Вывод формул для площадей четырехугольников Вывод формул для площадей четырехугольников |
 Вывод формулы Брахмагупты для площади вписанного четырехугольника Вывод формулы Брахмагупты для площади вписанного четырехугольника |
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.
Видео:Задача 6 №27917 ЕГЭ по математике. Урок 134Скачать

Формулы для площадей четырехугольников
| Четырехугольник | Рисунок | Формула площади | Обозначения | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Прямоугольник |  | S = ab | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Параллелограмм |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Квадрат |  | S = a 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | S = 4r 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ромб |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Трапеция |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | S = m h | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дельтоид |  | S = ab sin φ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Произвольный выпуклый четырёхугольник |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вписанный четырёхугольник |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Прямоугольник | ||
 | ||
 | ||
 | ||
| Параллелограмм | ||
 | ||
 | ||
 | ||
| Квадрат | ||
 | S = a 2 где | |
 | S = 4r 2 | |
 | ||
 | ||
| Ромб | ||
 | ||
 | ||
 | ||
 | ||
 | ||
| Трапеция | ||
 | ||
 | ||
 | ||
 | ||
| Дельтоид | ||
 | ||
 |  где | |
 | ||
 | ||
| Произвольный выпуклый четырёхугольник | ||
 | ||
| Вписанный четырёхугольник | ||
 | ||
| Прямоугольник |
 |
где
a и b – смежные стороны

где
d – диагональ,
φ – любой из четырёх углов между диагоналями

где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R

где
a – сторона,
ha – высота, опущенная на эту сторону

где
a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

где
a – сторона квадрата



Получается из верхней формулы подстановкой d = 2R

где
a – сторона,
ha – высота, опущенная на эту сторону

где
a – сторона,
φ – любой из четырёх углов ромба



где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

где
a и b – основания,
h – высота


φ – любой из четырёх углов между ними

где
a и b – основания,
c и d – боковые стороны ,

где
a и b – неравные стороны,
φ – угол между ними

где
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .

где
a и b – неравные стороны,
r – радиус вписанной окружности


φ – любой из четырёх углов между ними

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Вывод формул для площадей четырехугольников
Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле
Доказательство . В соответствии с рисунком 1 справедливо равенство:
что и требовалось доказать.
Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле
где a – сторона параллелограмма, а ha – высота высота высота , опущенная на эту сторону (рис. 2).
Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
что и требовалось доказать.
Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
то, в силу утверждения 2, справедлива формула
что и требовалось доказать.
Утверждение 4 . Площадь ромба ромба можно найти по формуле

где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
что и требовалось доказать.
Утверждение 5 . Площадь трапеции можно найти по формуле

где a и b – основания трапеции, а h – высота высота высота (рис.5).
Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому
что и требовалось доказать.
Утверждение 6 . Площадь трапеции трапеции можно найти по формуле
где a и b – основания, а c и d – боковые стороны трапеции ,
(рис.6).
Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

что и требовалось доказать.
Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то
📸 Видео
Найти площадь квадрата описанного около окружности радиуса 19Скачать

Геометрия Четырёхугольник ABCD вписан в окружность радиуса R = 8. Известно, что AB = BC = CD = 12Скачать

Геометрия. ОГЭ по математике. Задание 16Скачать

9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

112. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписаннойСкачать

Задача 6 №27910 ЕГЭ по математике. Урок 130Скачать


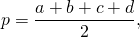
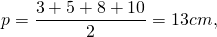
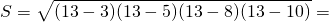
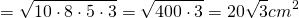
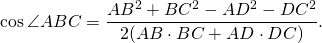
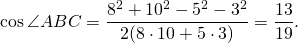
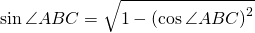
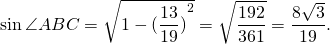
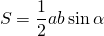
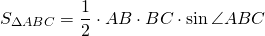
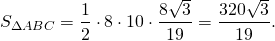
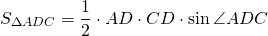
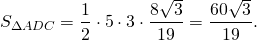
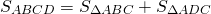
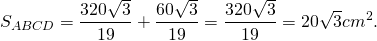
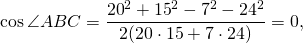
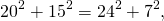
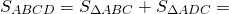
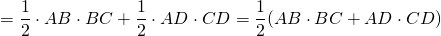
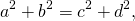















 ,
,























