Описанный четырехугольник свойства и признаки с доказательством

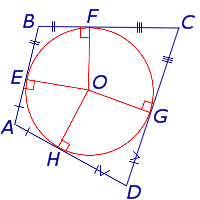
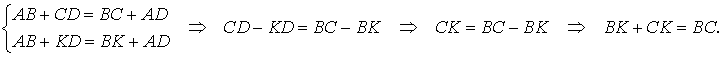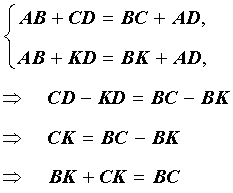Определение 1 . Окружностью, вписанной в четырёхугольник, называют окружность, которая касается касается каждой из сторон четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, описанным около окружности или описанным четырёхугольником .

Замечание . В настоящем разделе мы рассматриваем только выпуклые четырёхугольники.

Теорема 1 . Если четырёхугольник описан около окружности, то суммы длин его противоположных сторон равны.

Доказательство . Рассмотрим четырёхугольник ABCD , описанный около окружности, и обозначим буквами E, F, G, H – точки касания сторон четырёхугольника с окружностью (рис.2).

AH = AE, BF = BE, CF = CG, DH = DG,

Складывая эти равенства, получим:

AH + BF + CF + DH =
= AD + BC,
AE + BE + CG + DG =
= AB + CD,

то справедливо равенство

что и требовалось доказать.

Теорема 2 (обратная теорема к теореме 1) . Если у четырёхугольника суммы длин противоположных сторон равны, то в этот четырёхугольник можно вписать окружность.

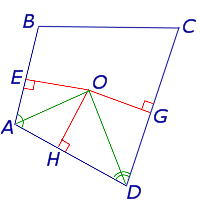
Доказательство . Рассмотрим четырёхугольник ABCD , длины сторон которого удовлетворяют равенству

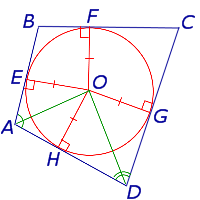
и проведём биссектрисы углов BAD и CDA . Обозначим точку пересечения этих биссектрис буквой O , и опустим из точки O перпендикуляры OH, OE и OG на стороны AD, AB и CD соответственно (рис.3).

Следовательно, справедливы равенства

из которых вытекает, что точки H, E и G лежат на окружности с центром в точке O и радиусом OH , касающейся сторон четырёхугольника AD, AB и CD в точках H, E и G соответственно. При этом возможны два случая:

Окружность касается касается стороны BC (рис.4).

В этом случае четырёхугольник ABCD описан около окружности, и теорема доказана.

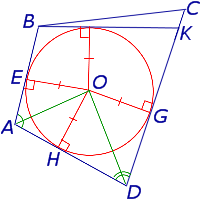
Окружность не касается стороны BC .

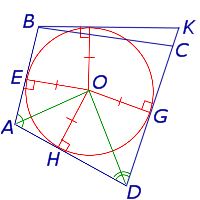
В этом случае касательная, проведенная к окружности из точки B , пересекает прямую DC в точке K , и возможны два случая:

Точка K лежит между точками C и D (рис.5)

Рассмотрим случай 2а и приведём его к противоречию. В этом случае в силу того, что четырёхугольник ABKD является описанным, а также по условию теоремы справедливы равенства:

Последнее равенство утверждает, что в треугольнике BKC сумма двух сторон равна третьей стороне, что противоречит неравенству треугольника неравенству треугольника неравенству треугольника . Полученное противоречие доказывает, что случай 2а невозможен.

Совершенно аналогичные рассуждения позволяют заключить, что случай 2b также невозможен.

Итак, возможен и реализуется лишь случай 1.

Из доказательства теоремы 2 непосредственно вытекает

Теорема 3 . Биссектрисы всех внутренних углов описанного четырёхугольника пересекаются в одной точке – центре вписанной окружности.

В следующей таблице приводятся примеры четырёхугольников, в которые можно вписать окружность. Доказательства утверждений непосредственно вытекают из теорем 1 и 2 и предоставляются читателю в качестве несложных упражнений.

Примеры описанных четырёхугольников

Фигура	Рисунок	Утверждение
Ромб		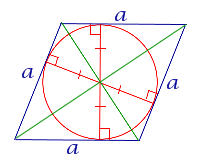В любой ромб можно вписать окружность
Квадрат		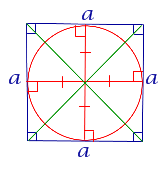В любой квадрат можно вписать окружность
Прямоугольник		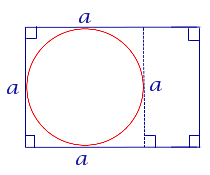В прямоугольник можно вписать окружность тогда и только тогда, когда он является квадратом
Параллелограмм		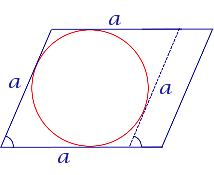В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом
Дельтоид		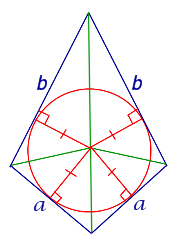В любой дельтоид можно вписать окружность
Трапеция		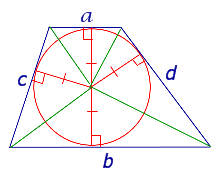В трапецию можно вписать окружность тогда и только тогда, когда у трапеции сумма длин боковых сторон рана сумме длин оснований

Ромб

Квадрат

В любой квадрат можно вписать окружность

Прямоугольник

В прямоугольник можно вписать окружность тогда и только тогда, когда он является квадратом

Параллелограмм

В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом

Дельтоид

Трапеция

В трапецию можно вписать окружность тогда и только тогда, когда у трапеции сумма длин боковых сторон рана сумме длин оснований

Please wait.

We are checking your browser. mathvox.ru

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6c6ab94a7a017b57 • Your IP : 178.45.231.185 • Performance & security by Cloudflare

Урок геометрии по теме «Свойство и признак описанного четырехугольника»

Презентация к уроку

Загрузить презентацию (130 кБ)

Образовательная. Создание условий для успешного усвоения понятия описанного четырёхугольника, его свойства, признака и овладения умениями применять их на практике.

Развивающая. Развитие математических способностей, создание условий для умения обобщать и применять прямой и обратный ход мыслей.

Воспитательная. Воспитание чувства красоты эстетикой чертежей, удивления необычным

решением, формирование организованности, ответственность за результаты своего труда.

1. Изучить определение описанного четырёхугольника.

2. Доказать свойство сторон описанного четырёхугольника.

3. Познакомить с двойственностью свойств сумм противоположных сторон и противоположных углов вписанного и описанного четырёхугольников.

4. Дать опыт практического применения рассмотренных теорем при решении задач.

5. Провести первичный контроль уровня усвоения нового материала.

Оборудование:

компьютер, проектор;
• учебник “Геометрия. 10-11 классы” для общеобразоват. учреждений: базовый и профил. уровни авт. А.В. Погорелов.

Программные средства: Microsoft Word, Microsoft Power Point.

Использование компьютера при подготовке учителя к уроку.

С помощью стандартной программы операционной системы Windows созданы к уроку:

1. Презентация.
2. Таблицы.
3. Чертежи.
4. Раздаточный материал.

План урока

Организационный момент. (2 мин.)

Проверка домашнего задания. (5 мин.)

Изучение нового материала. (28 мин.)

Самостоятельная работа. (7 мин.)

Домашнее задание.(1 мин.)

Итог урока. (2 мин.)

1. Организационный момент. Приветствие. Сообщение темы и цели урока. Запись в тетради даты и темы урока.

2. Проверка домашнего задания.

3. Изучение нового материала.

Работа над понятием описанного многоугольника.

Определение. Многоугольник называется описанным около окружности, если все его стороны касаются некоторой окружности.

Вопрос. Какие из предложенных многоугольников являются описанными, а какие не являются и почему?

Нарушение “касаются”	Рисунки 1 и 2
Нарушение “все стороны”	Рисунки 2 и 3
Нарушение “многоугольник”	Рисунок 6
Нарушение “некоторой окружности”	Рисунок 5 и 7

Доказательство свойств описанного четырёхугольника.

Теорема. В описанном четырёхугольнике суммы противоположных сторон равны.

Учащиеся работают с учебником, записывают формулировку теоремы в тетрадь.

1. Представить формулировку теоремы в форме условного предложения.

2. Каково условие теоремы?

3. Каково заключение теоремы?

Ответ. Если четырёхугольник описан около окружности, то суммы противолежащих сторон равны.

Проводится доказательство, учащиеся делают записи в тетради.

Учитель. Отметим двойственность ситуаций для сторон и углов описанного и вписанного четырёхугольников.

Закрепление полученных знаний.

Задачи.

Противоположные стороны описанного четырёхугольника 8 м и 12 м . Можно ли найти периметр?

Задачи по готовым чертежам.

Доказательство признака описанного четырёхугольника.

Сформулировать обратную теорему.

Ответ. Если в четырёхугольнике суммы противоположных сторон равны, то в него можно вписать окружность. (Вернуться к слайду 2, рис.7)

Учитель. Уточните формулировку теоремы.

Теорема. Если суммы противоположных сторон выпуклого четырёхугольника равны, то в него можно вписать окружность.

Работа с учебником. Познакомиться с доказательством признака описанного четырёхугольника по учебнику.

Применение полученных знаний.

3. Задачи по готовым чертежам.

1. Можно ли вписать окружность в четырёхугольник с противоположными сторонами 9 м и 4 м , 10 м и 3 м?

2. Можно ли вписать окружность в равнобокую трапецию с основаниями 1 м и 9 м, высотой 3 м?

Письменная работа в тетрадях.

Задача. Найти радиус окружности, вписанной в ромб с диагоналями 6 м и 8 м.

4. Самостоятельная работа.

1 вариант

1. Можно ли вписать окружность

1) в прямоугольник со сторонами 7 м и 10 м,

2. Противоположные стороны четырёхугольника, описанного около окружности, равны 7 м и 10 м.

Найти периметр четырёхугольника.

3. Равнобокая трапеция с основаниями 4 м и 16 м описана около окружности.

1) радиус вписанной окружности,

2) радиус описанной окружности.

2 вариант

1. Можно ли вписать окружность:

1) в параллелограмм со сторонами 6 м и 13 м,

2. Противоположные стороны четырёхугольника, описанного около окружности, равны 9 м и 11 м. Найти периметр четырёхугольника.

3. Равнобокая трапеция с боковой стороной 5 м описана около окружности с радиусом 2 м.

1) основание трапеции,

2) радиус описанной окружности.

5. Домашнее задание. П.86, № 28, 29, 30.

6. Итог урока. Проверяется самостоятельная работа, выставляются оценки.

📽️ Видео