Виды треугольников по теореме пифагора

Треугольники бывают остроугольными, тупоугольными, прямоугольными, разносторонними, равносторонними, равнобедренными.

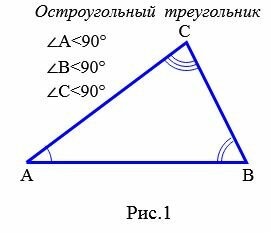
Определение 1. Треугольник называется остроугольным, если все ее углы острые, т.е. меньше 90° (Рис.1).

Определение 2. Треугольник называется тупоугольным, если один из его углов тупой, т.е. больше 90° (Рис.2).

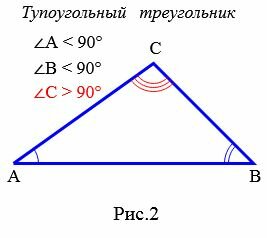Если треугольник тупоугольный, то исходя из того, что сумма всех углов треугольника равна 180°, остальные два угла треугольника будут острыми.

Определение 3. Треугольник называется прямоугольным, если один из его углов прямой, т.е. равен 90° (Рис.3).

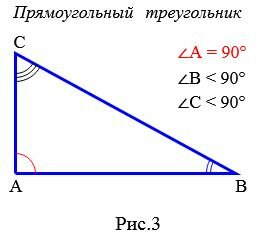Если треугольник прямоугольный, то исходя из того, что сумма всех углов треугольника равна 180°, остальные два угла треугольника будут острыми.

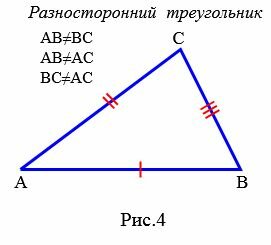
Определение 4. Треугольник называется разносторонним, если длины всех сторон треугольника разные (Рис.4).

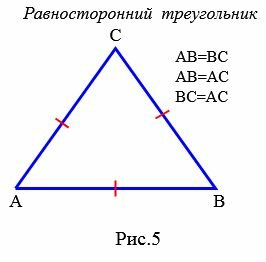
Определение 5. Треугольник называется равносторонним или правильным, если длины всех сторон равны (Рис.5).

Определение 6. Треугольник называется равнобедренным, если длины двух сторон равны (Рис.6).

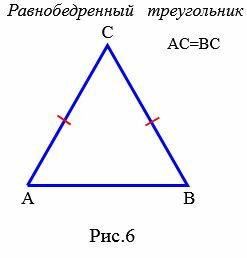В равнобедренном треугольнике равные стороны называются боковыми сторонами треугольника, а третья сторона называется основанием.

Видео:Виды треугольниковСкачать

Теорема Пифагора

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Основные понятия

Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Гипотенуза — сторона, лежащая напротив прямого угла.

Катет — одна из двух сторон, образующих прямой угол.

Формула Теоремы Пифагора выглядит так:

где a, b — катеты, с — гипотенуза.

Из этой формулы можно вывести следующее:

• a = √c 2 − b 2
• b = √c 2 − a 2
• c = √a 2 + b 2

Для треугольника со сторонами a, b и c, где c — большая сторона, действуют следующие правила:

• если c 2 2 + b 2 , значит угол, противолежащий стороне c, является острым.
• если c 2 = a 2 + b 2 , значит угол, противолежащий стороне c, является прямым.
• если c 2 > a 2 +b 2 , значит угол, противолежащий стороне c, является тупым.

Видео:8 класс, 16 урок, Теорема ПифагораСкачать

Теорема Пифагора: доказательство

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дано: ∆ABC, в котором ∠C = 90º.

Доказать: a 2 + b 2 = c 2 .

Пошаговое доказательство:

• Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
• Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:

• Также прямоугольная фигура ∆CBH подобна ∆ABC:

• Введем новые обозначения: BC = a, AC = b, AB = c.

• Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.

• Значит a 2 = c * HB, b 2 = c * AH.
• Сложим полученные равенства:

a 2 + b 2 = c * HB + c * AH

a 2 + b 2 = c * (HB + AH)

a 2 + b 2 = c * AB

Видео:ВСЕ ВИДЫ ТРЕУГОЛЬНИКОВ😉 #егэ #огэ #математика #профильныйегэ #shorts #геометрия #образованиеСкачать

Обратная теорема Пифагора: доказательство

Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник является прямоугольным.

Дано: ∆ABC

Доказать: ∠C = 90º

Пошаговое доказательство:

• Построим прямой угол с вершиной в точке C₁.
• Отложим на его сторонах отрезки C₁A₁ = CA и C₁B₁ = CB.

• Проведём отрезок A₁B₁.
• Получилась фигура ∆A₁B₁C₁, в которой ∠C₁=90º.

• В этой фигуре ∆A₁B₁C₁ применим теорему Пифагора: A₁B₁ 2 = A₁C₁ 2 + B₁C₁ 2 .
• Таким образом получится:

• Значит, в фигурах треугольниках ∆ABC и ∆A₁B₁C₁:

1. C₁A₁ = CA и C₁B₁ = CB по результату построения,
2. A₁B₁ = AB по доказанному результату.

• Поэтому, ∆A₁B₁C₁ = ∆ABC по трем сторонам.
• Из равенства фигур следует равенство их углов: ∠C =∠C₁ = 90º.

Обратная теорема доказана.

Видео:Теорема Пифагора. 8 КЛАСС | Математика | TutorOnlineСкачать

Решение задач

Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 8 см. Какое значение у гипотенузы?

Как решаем:

Пусть катеты a = 6 и b = 8.

По теореме Пифагора c 2 = a 2 + b 2 .

Подставим значения a и b в формулу:
c 2 = 6 2 + 8 2 = 36 + 64 = 100
c = √100 = 10.

Задание 2. Является ли треугольник со сторонами 8 см, 9 см и 11 см прямоугольным?

• Выберем наибольшую сторону и проверим, выполняется ли теорема Пифагора:

Ответ: треугольник не является прямоугольным.

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Виды треугольников

Треугольники различаются между собой по характеру углов и по характеру сторон.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Виды треугольников по углам

1. Остроугольный треугольник – это треугольник, у которого все углы острые, то есть меньше 90°.
2. Прямоугольный треугольник – это треугольник, у которого один из углов является прямым, то есть равен 90°.

Стороны, образующие прямой угол называются катетами, а сторона, лежащая напротив прямого угла, называется гипотенузой.

Видео:Виды треугольниковСкачать

Виды треугольников по сторонам

1. Разносторонний треугольник – это треугольник, у которого все стороны имеют разную длину.
2. Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой.

Равные стороны называются боковыми сторона треугольника, а третья сторона, не равная двум другим, называется его основанием.

📺 Видео

Виды треугольников. Построение треугольника | Математика 4 класс #38 | ИнфоурокСкачать

Геометрия 7 кл. Треугольники. Определение. Обозначение. Компоненты. Особенности. Виды треугольников.Скачать

Треугольники. 7 класс.Скачать

Виды треугольников. 6 классСкачать

Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Задача по геометрии на прямоугольный треугольник и теорему Пифагора из реального ОГЭ по математикеСкачать

Теорема Пифагора для чайников)))Скачать

Edu: Сколькими способами можно доказать теорему Пифагора?Скачать

ЕГЭ 2024. ВСЁ ПРО ТРЕУГОЛЬНИКИ за 15 минутСкачать

Математика 6 класс. Треугольник. Виды треугольников. ЕГЭ, ОГЭ, ЦТ, экзаменСкачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Виды треугольников. Видеоурок по геометрии 7 классСкачать