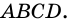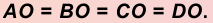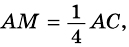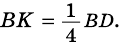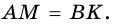Если все стороны четырехугольника равны то этот четырехугольник является квадратом

Квадратом называют прямоугольник, у которого все стороны равны.

На рисунке 57 изображен квадрат

Сформулируем свойства квадрата.

1. Все углы квадрата прямые.

2. Периметр квадрата

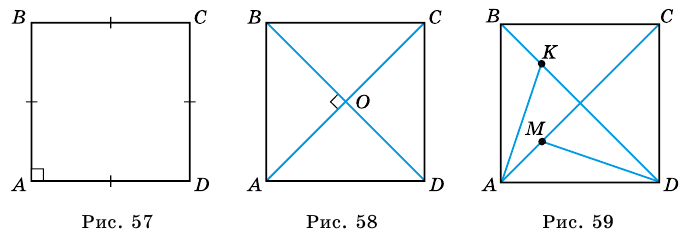
3. Диагонали квадрата равны (рис. 58).

4. Диагонали квадрата взаимно перпендикулярны и точкой пересечения делятся пополам (рис. 58).

5. Диагонали квадрата делят его углы пополам, то есть образуют углы по 45° со сторонами квадрата (рис. 58).

6. Точка пересечения диагоналей квадрата равноудалена от всех его вершин:

Пример:

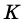
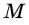
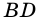
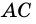
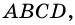
Точки и принадлежат соответственно диагоналям и квадрата причем

Докажите, что 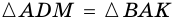(рис. 59). 4

Доказательство:

1) (по свойству квадрата), (как стороны квадрата).

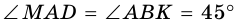
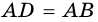
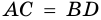
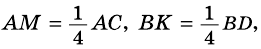
2) Так как (по свойству диагоналей квадрата) и

то

3) Тогда 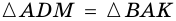(по двум сторонам и углу между ними).

Рассмотрим признаки квадрата.

Теорема (признаки квадрата). 1) Если у прямоугольника диагонали взаимно перпендикулярны, то он является квадратом. 2) Если у ромба диагонали равны, то он является квадратом.

Доказательство:

1) Данный прямоугольник является параллелограммом, а параллелограмм со взаимно перпендикулярными диагоналями — ромбом. Следовательно, у данного прямоугольника все стороны равны, поэтому он является квадратом.

2) Данный ромб является параллелограммом, а параллелограмм с равными диагоналями — прямоугольником. Следовательно, у данного ромба все углы прямые, поэтому он является квадратом.

Пример:

Докажите, что если в четырехугольнике все стороны равны и все углы равны, то этот четырехугольник — квадрат.

Доказательство:

1) Так как в четырехугольнике все углы равны, то, по признаку прямоугольника, он является прямоугольником.

2) Так как в прямоугольнике все стороны равны, то он является квадратом.

Термин «квадрат» происходит от латинского quadratum (quadrate -сделать четырехугольным).

Известный историк математики Д. Д. Мордухай-Болтовский (1876-1952) писал: «Первым четырехугольником, с которым познакомилась геометрия, был квадрат».

• Трапеция и ее свойства
• Площадь трапеции
• Центральные и вписанные углы
• Углы и расстояния в пространстве
• Параллелограмм, его свойства и признаки
• Площадь параллелограмма
• Прямоугольник и его свойства
• Ромб и его свойства, определение и примеры

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Если все стороны четырехугольника равны то этот четырехугольник является квадратом

Какое из следующих утверждений верно?

1) Две различные прямые, перпендикулярные третьей прямой, параллельны.

2) Если диагонали выпуклого четырёхугольника равны и перпендикулярны, то этот четырёхугольник является квадратом.

3) Все углы ромба равны.

В ответе запишите номер выбранного утверждения.

1) Две различные прямые, перпендикулярные третьей прямой, параллельны — верно.

2) Если диагонали выпуклого четырёхугольника равны и перпендикулярны, то этот четырёхугольник является квадратом — неверно, если точка пересечения диагоналей не является серединой каждой из них, то четырехугольник не будет являться квадратом.

3) Все углы ромба равны — неверно.

В ответе запишите номер выбранного утверждения.

Видео:Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

Квадрат, его свойства и признаки.

Видео:Геометрия 8. Урок 4 - Прямоугольник, ромб, квадрат - свойства и признаки.Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Квадрат, его свойства и признаки.

Определение. Квадратом называется прямоугольник, у которого все стороны равны.

Для квадрата можно ввести несколько определений. Самое ёмкое мы уже привели. Но можно определить квадрат следующим образом:

Квадратом называется четырёхугольник, у которого все стороны равны, а углы прямые.

Квадратом называется параллелограмм, у которого все стороны и углы равны.

Квадратом называется ромб, у которого все углы прямые.

Поскольку квадрат является и параллелограммом, и прямоугольником, и ромбом, то он обладает теми же свойствами, что и все перечисленные четырёхугольники.

У квадрата диагонали пересекаются и точкой пересечения делятся пополам.

У квадрата диагонали взаимно перпендикулярны.

У квадрата диагонали являются биссектрисами его углов.

У квадрата диагонали равны.

У квадрата стороны являются высотами.

Каждая диагональ квадрата делит его на равные прямоугольные треугольники.

Теперь определим признаки квадрата.

ТЕОРЕМА ( I признак). Если в прямоугольнике две его смежные стороны равны, то он является квадратом.

Так как – прямоугольник, то у него противолежащие стороны равны.

– квадрат (по определению), ч.т.д.

ТЕОРЕМА ( II признак). Если в прямоугольнике диагонали перпендикулярны, то этот прямоугольник является квадратом.

по свойству диагоналей прямоугольника, значит, – медиана (по опред-нию).

– высота , т.к. . Значит, в является и медианой и высотой, поэтому этот треугольник является равнобедренным (по признаку равнобедренного треугольника), т.е. . Согласно I признаку квадрата, прямоугольник является квадратом, ч.т.д.

ТЕОРЕМА ( III признак). Если в прямоугольнике одна из диагоналей является биссектрисой его угла, то такой прямоугольник является квадратом.

Так как – биссектриса , то .

по свойству внутренних накрест лежащих углов при параллельных прямых. Значит, , следовательно – равнобедренный, и . По I признаку квадрата, прямоугольник является квадратом, ч.т.д.

ТЕОРЕМА ( IV признак). Если в ромбе диагонали равны, то этот ромб является квадратом.

по III признаку равенства треугольников. Значит, все соответствующие углы у этих треугольников равны, т.е. . Эти углы являются внутренними односторонними при параллельных прямых и , следовательно, их сумма равна , т.е. , а, значит, и . Так как в ромбе противолежащие углы равны, то и все остальные углы также равны по . Значит, такой ромб является квадратом, ч.т.д.

ТЕОРЕМА ( V признак). Если в параллелограмме диагонали перпендикулярны и равны, то такой параллелограмм является квадратом.

Так как , то по II признаку ромба, параллелограмм является ромбом.

Так как , то по IV признаку квадрата, ромб является квадратом, ч.т.д.

ТЕОРЕМА ( VI признак). Если в четырёхугольнике диагонали равны, взаимно перпендикулярны и точкой пересечения делятся пополам, то такой четырёхугольник является квадратом.

1. Так как , то четырёхугольник является параллелограммом (по признаку параллелограмма).

2. Так как , то параллелограмм является квадратом (по V признаку квадрата), ч.т.д.

ТЕОРЕМА ( VII признак). Если в четырёхугольнике все стороны равны и среди внутренних углов есть один прямой угол, то такой четырёхугольник является квадратом.

1. Так как , то четырёхугольник является ромбом (по V признаку ромба).

2. Так как , то ромб, который по определению является параллелограммом, является прямоугольником (по III признаку прямоугольника), значит, все углы в этом четырёхугольнике прямые.

3. Итак, прямоугольник , у которого все стороны равны, является квадратом (по определению), ч.т.д.

Если в прямоугольнике две его смежные стороны равны, то он является квадратом.

Если в прямоугольнике диагонали перпендикулярны, то этот прямоугольник является квадратом.

Если в прямоугольнике одна из диагоналей является биссектрисой его угла, то такой прямоугольник является квадратом.

Если в ромбе диагонали равны, то этот ромб является квадратом.

Если в параллелограмме диагонали перпендикулярны и равны, то такой параллелограмм является квадратом.

Если в четырёхугольнике диагонали равны, взаимно перпендикулярны и точкой пересечения делятся пополам, то такой четырёхугольник является квадратом.

Если в четырёхугольнике все стороны равны и среди внутренних углов есть один прямой угол, то такой четырёхугольник является квадратом.

Периметр квадрата равен см. Найдите сторону квадрата .

На рисунке четырёхугольник – квадрат, . Докажите, что выпуклый четырёхугольник также является квадратом.

На рисунке четырёхугольник – прямоугольник, . Докажите, что выпуклый четырёхугольник является квадратом.

В треугольнике . На сторонах и взяты точки и , а на стороне – точки и так, что четырёхугольник является квадратом, . Найдите .

В треугольнике . На сторонах отмечены точки соответственно так, что четырёхугольник является квадратом, . Найдите .

На сторонах и квадрата отмечены точки и соответственно, . Отрезки и пересекаются в точке . Найдите .

На сторонах квадрата отмечены соответственно точки . Сравните отрезки и .

На катетах и прямоугольного треугольника построены квадраты и . Докажите, что сумма расстояний от точек и до прямой равна .

На катетах и прямоугольного треугольника построены квадраты и . Прямые и пересекаются в точке . Докажите, что .

Длина проекции одной из сторон квадрата на его диагональ равна . Найдите длину диагонали.

В четырёхугольнике диагонали взаимно перпендикулярны. Докажите, что отрезки, соединяющие середины противоположных сторон, равны.

Дан квадрат . Докажите, что – квадрат.

Дан квадрат . Докажите, что – ромб.

Дан квадрат . На стороне взята точка такая, что . Докажите, что точки – вершины равнобедренного треугольника.

Дан квадрат . Точки – середины его сторон соответственно. Докажите, что .

Дан квадрат . Точки и делят его стороны и так, что . Докажите, что .

Квадраты и имеют общую вершину . Докажите, что медиана треугольника перпендикулярна отрезку .

Внутри квадрата взята точка так, что . Докажите, что треугольник равносторонний.

На рисунке – квадрат, точка принадлежит , точка принадлежит , точка принадлежит , прямые и пересекаются в точке . Докажите, что .

В равнобедренный прямоугольный треугольник, каждый катет которого равен см, вписан квадрат, имеющий с ним один общий угол. Найдите периметр квадрата.

В равнобедренный прямоугольный треугольник вписан квадрат так, что две его вершины находятся на гипотенузе, а две другие – на катетах. Определите сторону квадрата, если известно, что гипотенуза равна 30 дм.

В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Определите стороны этого прямоугольника, зная, что одна из них втрое больше другой и что диагональ квадрата равна дм.

В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Определите стороны этого прямоугольника, зная, что одна из них вдвое больше другой и что диагональ квадрата равна см.

Точка расположена во внутренней области квадрата так, что расстояния от неё до сторон и пропорциональны соответственно числам и , а расстояние от до прямой равно см. Найдите периметр этого квадрата.

Точка расположена во внутренней области квадрата так, что расстояния от неё до сторон и пропорциональны соответственно числам и , а расстояние от до прямой равно м. Найдите периметр этого квадрата.

Точка лежит на стороне квадрата . Высоты треугольников и , проведённые из точки , равны соответственно и . Найдите произведение длин диагоналей этого квадрата.

Точка расположена во внутренней области квадрата так, что расстояния от неё до сторон и пропорциональны соответственно числам и , а расстояние от до прямой равно м. Найдите периметр этого квадрата.

Точка лежит на стороне квадрата . Высоты треугольников и , проведённые из точки , равны соответственно и . Найдите произведение длин диагоналей этого квадрата.

На сторонах и квадрата отмечены точки и соответственно так, что . Определите взаимное расположение прямых и .

В равнобедренный прямоугольный треугольник вписан квадрат , имеющий с ним общий угол . Найдите периметр квадрата, если катет треугольника равен см.

Внутри квадрата отмечена такая точка , что треугольник равносторонний. Найдите угол .

В равнобедренный прямоугольный треугольник вписан квадрат , имеющий с ним общий прямой угол. Найдите катет треугольника, если периметр квадрата равен см.

Внутри квадрата отмечена такая точка , что треугольник равносторонний. Найдите угол .

Через вершины квадрата проведены прямые, параллельные его диагоналям. Определите вид образованного ими четырёхугольника и вычислите его периметр, если диагональ квадрата равна см.

Через точку – точку пересечения диагоналей квадрата проведена прямая, параллельная стороне и пересекающая стороны и в точках и соответственно. Найдите периметр квадрата, если известно, что .

Найдите периметр квадрата по данным на рисунке.

💥 Видео

Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

3 правила для вписанного четырехугольника #shortsСкачать

№400. Докажите, что если в четырехугольнике все углы прямые, то четырехугольник — прямоугольник.Скачать

Прямоугольник. 8 класс.Скачать

Признак параллелограмма (если в четырехугольнике две стороны равны и параллельны, тоСкачать

Математика 5 класс (Урок№29 - Четырёхугольники.)Скачать

9 класс. Геометрия. ОГЭ. Окружность. Четырехугольники.Скачать

Геометрия 8 класс (Урок№6 - Прямоугольник. Ромб. Квадрат.)Скачать

№410. Является ли четырехугольник квадратом, если его диагонали: а) равны и взаимноСкачать

Найти периметр четырехугольника, вершины которого лежат на серединах сторон другого четырехугольникаСкачать

8 класс, 8 урок, Ромб и квадратСкачать

Диагонали четырехугольника равны 4 и 5.Скачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Геометрия Признак параллелограмма: Если в четырехугольнике противолежащие стороны равныСкачать

Прямоугольник. Что такое прямоугольник?Скачать

№366. Найдите стороны четырёхугольника, если его периметр равен 8 смСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать