Больше объем понятия многоугольник четырехугольник трапеция (8 видео)

Больше объем понятия многоугольник четырехугольник трапеция

Определение и задачи логики

Определение логики. Для того чтобы определить, что такое логика, мы должны предварительно выяснить, в чём заключается цель человеческого познания. Цель познания заключается в достижении истины при помощи мышления, цель познания есть истина. Логика же есть наука, которая показывает, как должно совершаться мышление, чтобы была достигнута истина; каким правилам мышление должно подчиняться для того, чтобы была достигнута истина. При помощи мышления истина иногда достигается, а иногда не достигается. То мышление, при помощи которого достигается истина, должно быть названо правильным мышлением. Таким образом, логика может быть определена как наука о законах правильного мышления, или наука о законах, которым подчиняется правильное мышление.

Из этого определения видно, что логика исследует законы мышления. Но так как исследование законов мышления как известного класса психических процессов является также предметом психологии, то предмет логики выяснится лучше в том случае, если мы рассмотрим отличие логики от психологии в исследовании законов мышления.

Психология и логика. На мышление мы можем смотреть с двух точек зрения. Мы можем на него смотреть, прежде всего, как на известный процесс, законы которого мы исследуем. Это будет точка зрения психологическая. Психология изучает, как совершается процесс мышления. С другой стороны, мы можем смотреть на мышление, как на средство достижения истины. Логика исследует, каким законам должно подчиняться мышление, чтобы оно могло привести к истине.

Итак, разница между психологией и логикой в отношении к процессу мышления может быть выражена следующим образом. Психология рассматривает безразлично всевозможные роды мыслительной деятельности: рассуждение гения, бред больного, мыслительный процесс ребёнка, животного – для психологии представляют одинаковый интерес, потому что она рассматривает только, как осуществляется процесс мышления; логика же рассматривает условия, при которых мысль может быть правильной. В этом отношении логика сближается с грамматикой. Подобно тому, как грамматика указывает правила, которым должна подчиняться речь, чтобы быть правильной, так логика указывает нам законы, которым должно подчиняться наше мышление для того, чтобы быть правильным.

Для того чтобы понять утверждение, что существуют известные правила, которым должно подчиняться мышление, рассмотрим, в чём заключается задача логики.

Задача логики. Есть положения или факты, истинность которых усматривается непосредственно, и есть положения или факты, истинность которых усматривается посредственно, именно через посредство других положений или фактов. Если я скажу: «я голоден», «я слышу звук», «я ощущаю тяжесть», «я вижу, что этот предмет большой», «я вижу, что этот предмет движется» и т.п., то я выражу факты, которые должны считаться непосредственно познаваемыми. Такого рода факты мы можем назвать также непосредственно очевидными, потому что они не нуждаются ни в каком доказательстве: их истинность очевидна без доказательств. В самом деле, разве я нуждаюсь в доказательстве, что передо мной находится предмет, имеющий зелёный цвет? Неужели, если бы кто-нибудь стал доказывать, что этот предмет не зелёный, а чёрный, я поверил бы ему? Этот факт для меня непосредственно очевиден. К числу непосредственно очевидных положений относятся, прежде всего, те положения, которые являются результатом чувственного восприятия.

Все те факты, которые совершаются в нашем отсутствии (например, прошедшие явления, а также и будущие), могут быть познаваемы только посредственно. Я вижу, что дождь идёт, – это факт непосредственного познания; что ночью шёл дождь, есть факт посредственного познания, потому что я об этом узнаю через посредство другого факта, именно того факта, что почва мокрая. Факты посредственного познания или просто посредственное познание является результатом умозаключения, вывода. По развалинам я умозаключаю, что здесь был город. Если бы я был на этом месте тысячу лет назад, то я непосредственно воспринял бы этот город. По следам я заключаю, что здесь проехал всадник. Если бы я был здесь час назад, то я непосредственно воспринял бы самого всадника.

Посредственное знание доказывается, делается убедительным, очевидным при помощи знаний непосредственных. Этот последний процесс называется доказательством.

Таким образом, есть положения, которые не нуждаются в доказательствах, и есть положения, которые нуждаются в доказательствах и очевидность которых усматривается посредственно, косвенно.

Если есть положения, которые нуждаются в доказательствах, то в чём же заключается доказательство? Доказательство заключается в том, что мы положения неочевидные стараемся свести к положениям или фактам непосредственно очевидным или вообще очевидным. Такого рода сведение положений неочевидных к положениям очевидным лучше всего можно видеть на доказательствах математических. Если возьмём, например, теорему Пифагора, то она на первый взгляд совсем не очевидна.

Но если мы станем её доказывать, то, переходя от одного положения к другому, мы придём в конце концов к аксиомам и определениям, которые имеют непосредственно очевидный характер. Тогда и самая теорема сделается для нас очевидной. Таким образом, познание посредственное нуждается в доказательствах; познание непосредственное в доказательствах не нуждается и служит основой для доказательства познаний посредственных.

Заметив такое отношение между положениями посредственно очевидными и положениями непосредственно очевидными, мы можем понять задачи логики. Когда мы доказываем что-либо, т.е. когда мы сводим неочевидные положения к непосредственно очевидным, то в этом процессе сведения мы можем сделать ошибку: наше умозаключение может быть ошибочным. Но существуют определённые правила, которые показывают, как отличать умозаключения правильные от умозаключений ошибочных. Эти правила указывает логика. Задача логики поэтому заключается в том, чтобы показать, каким правилам должно следовать умозаключение, чтобы быть верным. Если мы эти правила знаем, то мы можем определить, соблюдены ли они в том или другом процессе умозаключения.

Из такого определения задач логики можно понять значение логики.

Значение и польза логики. Для выяснения значения логики обыкновенно принято исходить из определения её. Мы видели, что логика определяется как наука о законах правильного мышления. Из этого определения логики, по-видимому, следует, что стоит изучить законы правильного мышления и применять их в процессе мышления, чтобы можно было мыслить вполне правильно. Многим даже кажется, что логика может указывать средства для открытия истины в различных областях знания.

Но в действительности это неверно. Логика не поставляет своею целью открытие истин, а ставит своею целью доказательство уже открытых истин. Логика указывает правила, при помощи которых могут быть открыты ошибки. Вследствие этого, благодаря логике можно избежать ошибок. Поэтому становится понятным утверждение английского философа Дж. С. Милля, что польза логики главным образом отрицательная. Её задача заключается в том, чтобы предостеречь от возможных ошибок. Вследствие этого практическая важность логики чрезвычайно велика. «Когда я принимаю в соображение, – говорит Дж. С. Милль, – как проста теория умозаключения, какого небольшого времени достаточно для приобретения полного знания её принципов и правил и даже значительной опытности в их применении, я не нахожу никакого извинения для тех, кто, желая заниматься с успехом каким-нибудь умственным трудом, упускает это изучение. Логика есть великий преследователь тёмного и запутанного мышления; она рассеивает туман, скрывающий от нас наше невежество и заставляющий нас думать, что мы понимаем предмет, в то время когда мы его не понимаем. Я убеждён, что в современном воспитании ничто не приносит большей пользы для выработки точных мыслителей, остающихся верными смыслу слов и предложений и находящихся постоянно настороже против терминов неопределённых и двусмысленных, как логика».

Содержание

Лекция 6. Объем и содержание понятия. Отношения между понятиями.
«Управление общеобразовательной организацией: новые тенденции и современные технологии»
Лекция 4. Математические понятия и методика их формирования.
📹 Видео

Видео:Многоугольники. Математика 8 класс | TutorOnlineСкачать

Лекция 6. Объем и содержание понятия. Отношения между понятиями.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Лекция 4. Объем и содержание понятия. Отношения между понятиями.

Всякий математический объект обладает определенными свойствами. Например, квадрат имеет четыре стороны, четыре прямых угла и др. Различают свойства существенные и несущественные.

Существенное свойство — свойство, без которого объект не может существовать.

Несущественное свойство — свойство, отсутствие которого не влияет на существование объекта.

Для квадрата: АВСД существенные свойства: АВ = ВС = СД =ДА,

несущественные свойства: АВ, ДС — горизонтальны, АД, ВС — вертикальны.

Если квадрат повернуть, сохранятся только существенные свойства, именно они и составляют понятие об объекте.

Рассмотрим пример для дошкольников, используя наглядный материал

— Маленький черный треугольник.

— Большой белый треугольник.

— Чем фигуры похожи?

— Чем фигуры отличаются?

— Что есть у треугольника?

— 3 стороны, 3 угла.

Таким образом, дети выясняют существенные и несущественные свойства понятия «треугольник». Существенные свойства — «иметь три стороны и три угла», несущественные свойства — цвет и размеры.

Совокупность всех существеннных свойств объекта называют содержанием понятия.

Совокупность всех объектов, обозначаемая одним термином, составляет объем понятия.

Например, содержание понятия «квадрат» — это совокупность всех существенных свойств, которыми обладают квадраты, а в объем этого понятия входят квадраты различных размеров.

Итак, любое понятие характеризуется:

— объемом (совокупность всех объектов, называемых этим термином);

— содержанием (совокупность всех существенных свойств объектов, входящих в объем понятия).

Между объемом понятия и его содержанием существует связь: чем «больше» объем понятия, тем «меньше» его содержание, и наоборот. Объем понятия «треугольник» «больше», чем объем понятия «прямоугольный треугольник», так как все объекты второго понятия являются и объектами первого понятия. Содержание понятия «треугольник» «меньше», чем содержание понятия «прямоугольный треугольник», так как прямоугольный треугольник обладает всеми свойствами любого треугольника и еще другими свойствами, присущими только ему.

Для распознавания объекта необязательно проверять у него все существенные свойства, достаточно лишь некоторых. Этим пользуются, когда понятию дают определение.

Определение понятия – это логическая операция, которая раскрывает содержание понятия либо устанавливает значение термина. Определение понятия позволяет отличать определяемые объекты от других объектов. Так, например, определение понятия «прямоугольный треугольник» позволяет отличить его от других треугольников.

Различают явные и неявные определения. Явные определения имеют форму равенства двух понятий. Одно из них называют определяемым другое определяющим.

Например: «Квадрат – это прямоугольник, у которого все стороны равны». Здесь определяемое понятие – «квадрат», а определяющее — «прямоугольник, у которого все стороны равны».

Самый распространенный вид явных определений — это определение через род и видовое отличие. Приведенное выше определение квадрата относится к таким определениям. Действительно, понятие «прямоугольник», содержащееся в определяющем понятии, является ближайшим родовым понятием по отношению к понятию «квадрат», а свойство «иметь все равные стороны» позволяет из всех прямоугольников выделить один из видов — квадраты.

Следует иметь в виду, что понятия рода и вида относительны. Так, «прямоугольник» – это родовое к понятию «квадрат», но видовое по отношению к понятию «четырехугольник».

Кроме того, для одного понятия могут существовать несколько родовых. Например, для квадрата родовыми являются ромб, четырехугольник, многоугольник, геометрическая фигура. В определении через род и видовое отличие для определяемого понятия принято называть ближайшее родовое понятие.

Таким образом, определение через род и видовое отличие имеет следующую структуру:

Определяемое = Род + Видовое

Задания для самостоятельной работы по теме:

1. Каков объем понятий: «цифра», «автомобиль», «снегурочка», «волк», «столица России», «двузначное число».

2. Решите анаграммы. Исключите лишнее слово. Ответ обоснуйте:

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Лекция 4. Математические понятия и методика их формирования.

1. Понятие как форма мышления. Содержание и объем понятия.

2. Определение понятия, виды определений. Классификация понятий.

3. Методика изучения понятий в курсе средней школы (пропедевтика, введение, усвоение, закрепление, предупреждение ошибок).

1.Познание окружающего мира осуществляется в диалектическом единстве чувственной и рациональной форм мышления. К чувственным формам мышления относятся: ощущение, восприятие, представление. К рациональным формам мышления относятся: понятия, суждения, умозаключения. Ощущение и восприятие—первые сигналы действительности. На их основе образуются общие представления, а от них в результате сложной умственной деятельности мы переходим к понятиям.

Понятие — это форма мышления, в которой отражаются существенные признаки (свойства) объектов реального мира.

Свойство является существенным, если оно присуще этому объекту и без него оно не может существовать. Например, формальное понятие куба (различные кубы, размеры, цвета, материалы). При наблюдении их возникает восприятие объекта, следовательно, возникает представление об этих объектах в сознании. Затем, выделяя существенные признаки, формируется понятие.

Итак, понятие абстрагируется от индивидуальных черт и признаков отдельных восприятий и представлений, и является результатом обобщения восприятий и представлений очень большого количества однородных явлений и предметов.

Всякое понятие имеет две логические характеристики: содержание и объем.

Содержанием понятия называется совокупность существенных, взаимосвязанных признаков (свойств) объекта.

Объемом понятия называется совокупность объектов, обозначаемых одним и тем же термином (названием).

Например, термин (название) — трапеция.

2) одна пара противолежащих сторон параллельна,

3) другая пара противолежащих сторон не параллельна,

4) сумма углов прилежащих к боковой стороне равна .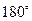

Объем понятия – все мыслимые трапеции.

Между содержанием понятия и объемом существует следующая связь: чем больше объем понятия, тем меньше его содержание, и наоборот. Так, например, объем понятия «равнобедренный треугольник» меньше объема понятия «треугольник». А содержание первого понятия больше содержания второго, ибо равнобедренный треугольник обладает не только всеми свойствами треугольника, но и особыми свойствами присущими только равнобедренным треугольникам (боковые стороны равны, углы при основании равны). Итак, если увеличить содержание, то уменьшится объем понятия.

Если объем одного понятия входит как часть в объем другого понятия, то первое понятие называют видовым, а второе родовым.

Например, ромб—это параллелограмм, у которого все стороны равны (Погорелов, 8 класс). Ромб — видовое, параллелограмм — родовое.

Квадрат—это прямоугольник, у которого все стороны равны (Погорелов, 8 класс). Квадрат — видовое, прямоугольник — родовое.

Но, квадрат—это ромб, у которого угол прямой.

То есть понятие рода и вида относительны.

Каждое понятие связано со словом-термином, которое соответствует данному понятию. В математике понятие часто обозначается символом ( ‌‌‌‌║). Термины и символы — это средства, которые служат для выражения и фиксирования математических понятий, для передачи и обработки информации о них.

2. В содержание понятия о каком-либо математическом объекте входит много различных существенных свойств этого объекта. Однако чтобы распознать объект, установить принадлежит ли он к данному понятию или нет, достаточно проверить наличие у него некоторых существенных свойств.

Определение понятия — формулировка предложения, в котором перечисляются необходимые и достаточные признаки понятия. Таким образом, содержание понятия раскрывается через определение.

Виды определений понятий.

1.Определение через ближайший род и видовое отличие.

Подчеркнем, что в качестве видового отличия всегда берется несущественный признак родового понятия, который для определяемого понятия является уже существенным.

Способ его образования (построения, происхождения)

Термин

2. Конструктивные (генетические) определения. (Генезис-происхождение).

Больше объем понятия многоугольник четырехугольник трапеция

Свойства объекта в таком определении раскрываются путем показа операций его конструирования.

Пример, треугольники называются равными, если у них соответствующие стороны и соответствующие углы равны (Погорелов, 7 класс). Это определение подсказывает учащимся, как построить треугольник равный данному.

3.Определения — условные соглашения. Те же конструктивные определения, но основанные на некотором соглашении. Такие определения используются в школьном курсе математики при расширении понятия числа.

Например, .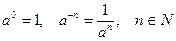

4. Индуктивные (рекурсивные). Указываются некоторые базисные объекты некоторого класса и правила, позволяющие получить новые объекты этого же класса.

Например. Числовая последовательность каждый член, которой, начиная со второго, равен предшествующему члену, сложенному с одним и тем же числом, называется арифметической прогрессией.

5. Отрицательные определения. Они не задают свойства объекта. Они выполняют как бы классификационную функцию. Например, скрещивающиеся прямые — это такие прямые, которые не принадлежат плоскости и не пересекаются.

6. Аксиоматическое определение. Определение через систему аксиом. Например, определение площади и объема.

Виды ошибок при определении понятий.

1) Определение должно быть соразмерно — в нём должно быть указано ближайшее родовое понятие к определяемому понятию (параллелограмм—это четырехугольник, параллелограмм—это многоугольник).

2) Определение не должно содержать «порочного круга» — первое определяется через второе, а второе через первое ( прямой угол равен девяносто градусов, один градус—это одна девяностая прямого угла).

3) Определение должно быть достаточным. В определении должны быть указаны все признаки, позволяющие однозначно выделить объекты определяемого понятия (смежными называются углы, которые в сумме дают ).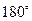

4) Определение не должно быть избыточным, то есть в определении не должно быть указано лишних признаков определяемого понятия. Например, ромб—это параллелограмм, у которого все стороны равны (Погорелов, 8 класс). Это определение избыточно, ибо достаточно равенства двух смежных сторон.

5) Определение не должно быть тавтологией, то есть повторяющей в любой словесной форме ранее сказанное. Например, равными треугольниками называются треугольники, которые равны между собой.

Логическая структура видовых отличий.

1. Видовые отличия могут быть связаны союзом «и» — конъюнктивная структура определения.

2. Видовые отличия связаны союзом «или» — дизъюнктивная структура определения.

3. Видовые отличия связаны словами «если…., то …» — импликативная структура.

Если с содержанием понятия связано определение, то с объемом связана классификация.

Классификация – это распределение объектов какого-либо понятия на взаимосвязанные классы (виды, типы) по наиболее существенным признакам (свойствам). Признак (свойство), по которому происходит классификация (деление) понятия на виды (классы), называется основанием классификации.

При проведении классификации необходимо соблюдать следующие правила:

1) В качестве основания классификации можно брать лишь один общий признак всех объектов данного понятия, он должен оставаться неизменным в процессе классификации.

2) Каждый объект понятия должен попасть в результате классификации в один и только один класс.

3) Классификация должна быть соразмерной, то есть объединение классов объектов составляют объем понятия (нет объекта, который не попал бы ни в один класс).

4) Классификация должна быть непрерывной, то есть в процессе классификации необходимо переходить к ближайшему (к данному) родовому понятию (виду).

В настоящее время в школьных учебниках термин классификация не употребляется, требования не указываются. Но это не значит, что учитель не классифицирует понятия. Классифицировать можно числа, функции, алгебраические выражения, геометрические преобразования, многоугольники, многогранники. Её можно оформлять в виде схемы, таблицы.

Учащихся следует подготавливать к построению классификации постоянно. На первом этапе учащимся следует предлагать готовые схемы, таблицы. На втором заполнение этих схем, таблиц. На третьем самостоятельное конструирование.

1. Классификация по видоизмененному признаку. Например, треугольник. Основание классификации: величина внутренних углов, члены: прямоугольные, остроугольные, тупоугольные.

2. Дихотомическая классификация (dicha и tome(греч)- «сечение на две части»). Оно представляет собой деление объема классифицируемого понятия на два противоречащих друг другу видовых понятия, одно из которых обладает данным признаком, а другое не обладает им.

Например,

3. При формировании понятия следует соблюдать три этапа: введение, усвоение, закрепление.

I. Введение может осуществляться двумя путями:

а) конкретно-индуктивный—все признаки понятия рассматриваются на примерах или задачах, после чего вводится термин и определение.

б) абстрактно-дедуктивным—сразу дается определение, а потом на примерах обрабатываются признаки.

Здесь прослеживаются две цели:

1) выучить определение.

2) Научить учащихся определять подходит ли объект под рассматриваемые понятия или нет. Этот этап осуществляется на специально составленных упражнениях.

Для реализации второй цели необходимо:

1) указывать систему необходимых и достаточных свойств объектов данного класса.

2) установить, обладает данный объект выделенными свойствами или нет.

3) заключить о принадлежности объекта к данному понятию.

III. Закрепление—решение более сложных задач, включающих рассматриваемые понятия.

Замечание 1. Формулируя определение понятия, следует обратить внимание на то, понятен ли учащимся смысл каждого слова, используемого в определении. В первую очередь следует обращать внимание на следующие слова: «каждый», «не более» и т.д.

Замечание 2. На этапе закрепления понятия следует предлагать задания не только на распознавание объекта, но и на отыскание следствий. Например, известно, что четырехугольник — трапеция ( и её основания). Назовите следствия, вытекающие из данных условий в силу определения трапеции.

Необходимы комплексные упражнения, выполнение которых основано только на использовании существенных свойств понятия, но и на отыскании следствий.

Например. Известно, что некоторый луч исходит из вершины угла. Следует ли отсюда, что этот луч является биссектрисой угла? Если нет, то измените, условие так, чтобы из него следовало, что луч являлся бы биссектрисой данного угла.

Замечание 3. Многие определения в ШКМ содержат знаки существования и общности (первообразная, четная функция, периодическая функция и т.д.). Работа по усвоению таких определений обладает некоторой специфичностью.

Пример. Функция f называется четной, если для любого x из её области определения f(-x)=f(x), причем область определения симметрична относительно начала координат, то есть для любого x из области определения число (-x)также принадлежит области определения. (f четна на М) .

Из этого определения можно получить условие непринадлежности функции к понятию четной функции, которое можно записать так:

(f не являетсячетной на М) .

Теперь можно подобрать систему упражнений на усвоение данного понятия:

1) Является ли функция f четной на множестве М, если:

А) для любого .

В) существует такой , что , а .

С) существует такой , что , а ?

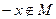
2) Известно, что функция h является четной на множестве М. Что от сюда следует?

3) Известно, что существует такой , что и . Можно ли утверждать, что функция является четной на множестве М? Если нет, то измените, условие так, чтобы из него следовало, что функция f была бы четной на М.