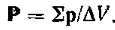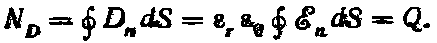Разобравшись с поведением диэлектрика на микроскопическом уровне, вернемся к плоскому конденсатору, изображенному на рис. 3.3. Откуда же взялись поляризационные заряды на поверхности диэлектрической пластины между обкладками?
Теперь мы знаем, что во внешнем поле, создаваемом обкладками, единица объема диэлектрика приобретает дипольный момент Р. Скажем, положительные заряды смещаются по направлению поля (вверх на рис. 3.3), а отрицательные — вниз. При полной однородности поля и диэлектрика объемные нескомпенсированные заряды внутри диэлектрика не появляются. Но такой сдвиг приводит к возникновению нескомпенсированных зарядов на поверхности диэлектрической пластины. Дипольный момент пластины равен VР, где V = Sd — ее объем. С другой стороны, полный поверхностный заряд на пластине равен
а расстояние между центрами положительных и отрицательных зарядов равно d (см. рис. 3.3). Поэтому дипольный момент пластины можно также записать как
Сравнивая эти два выражения, находим связь поверхностной плотности поляризационных зарядов с вектором поляризации
Напряженность Е суммарного поля внутри диэлектрика меньше напряженности поля E0, создаваемого обкладками. Именно поле Е действует на молекулы диэлектрика, именно его они «чувствуют», и потому для него справедливо соотношение (3.22)
Используя связь (3.3) напряженности поля Е ‘ поляризационных зарядов с суммарным полем Е
мы находим связь между диэлектрической проницаемостью и диэлектрической восприимчивостью
В общем случае вектор поляризации Р не параллелен вектору напряженности суммарного поля Е: в анизотропных диэлектриках вектор поляризации может поворачиваться относительно напряженности поля. Однако всегда мы можем записать соотношение
называется вектором электрического смещения (вектором электрической индукции).
В частном случае линейной зависимости поляризации от напряженности поля
вектор электрического смещения равен
где 
имеет место для изотропных диэлектриков. В общем случае вектор D не параллелен Е. Поле вектора D можно графически изобразить линиями электрического смещения, которые определяются так же, как и линии напряженности электрического поля (рис 3.23 и 3.24).
Рис. 3.23. Условия на плоской границе двух диэлектриков для напряженности и электрического смещения
Рис. 3.24. Линии напряженности и электрического смещения электрического поля
от точечного заряда, расположенного на границе раздела двух диэлектриков
В СИ единицей измерения электрического смещения является:
Видео:Урок 226. Плоский конденсаторСкачать

Векторы поляризованности и смещения
В предыдущей статье было показано, что вследствие поляризации диэлектрика, т. е. смещения его связанных зарядов, изменяется напряженность электрического поля. Результирующее влияние диэлектрика на электрическое поле оценивают векторной величиной, называемой поляризованностью Р (вектором поляризации).
Средняя интенсивность поляризации Pср определяется как сумма дипольных моментов в единице объема диэлектрика, а чтобы найти поляризованность в данном месте поля, надо выбрать достаточно малый объем ΔV:
Единица измерения поляризованности
[P] = [ql/V] = Кл*м/м 3 = Кл/м 2.
Вектор поляризации направлен навстречу вектору напряженности электрического поля связанных зарядов Eп.(рис. 4.12).
Вектор поляризации для большинства диэлектриков (за исключением группы сегнетоэлектриков) пропорционален напряженности электрического поля:
и его направление совпадает с направлением внешнего Eвн и результирующего Е полей (риc. 4.12).
Коэффициент k называется электрической восприимчивостью диэлектрика и характеризует его способность поляризоваться.
При расчетах электрических полей в диэлектриках с различными диэлектрическими проницаемостями пользуются еще вектором электрического смещения.
Электрическое смещение D связано с напряженностью электрического ноля простым соотношением
откуда можно определить единицу намерения электрического смещения:
которая такая же, как у вектора, поляризации и у поверхностной плотности зарядов на электродах.
Электрическое смещение и поверхностная плотность свободных зарядов численно одинаковы на поверхности всех проводящих тел, находящихся в электростатическом поле. Например, у внутренней поверхности пластины плоского конденсатора (рис. 4.8) напряженность однородного электрического поля, как и в любой точке однородного поля (4.10),
а электрическое смещение в любой точке поля, в том числе и у металлической поверхности,
т. е. совпадает с поверхностной плотностью заряда на пластине.
Из (2а) следует, что при заданной плотности поверхностных свободных зарядов на электродах электрическое смещение в однородном диэлектрике с диэлектрической проницаемостью εa не зависит от εa, а напряженность электрического поля зависит. Поэтому можно сказать, что на напряженность электрического поля определяется и свободными (на электродах) и связанными (в диэлектриках) зарядами, т. е. поляризацией диэлектрика, а электрическое смещение в однородном диэлектрике не зависит от связанных зарядов.
Связь между тремя векторными величинами, характеризующими электрическое поле в диэлектрике, выражается равенством
Приняв во внимание (1) и (2), получим
откуда диэлектрическая проницаемость
а электрическая восприимчивость

Рассмотрим еще неоднородное электрическое поле заряженного металлическою шара (рис. 1), радиус которого Rш. Известно, что электрический заряд Q находится на поверхности такого шара. Поверхностная плотность заряда
Поле металлического шара с зарядом Q совпадает вне шара с полем равного ему по значению точечного заряда Q, расположенного в центре шара (4.8); поэтому напряженность поля на расстоянии R от центра шара и в частности, у его наружной поверхности, т.е. при R = Rш,
а электрическое смещение
т. е. равно поверхностной плотности заряда.
Внутри металлического шара поля нет, как и во всяком проводнике в условиях электростатики , Поэтому потенциалы всех точек шара одинаковые, т. е. шар — эквипотенциальное тело, как и всякое металлическое тело в электростатическом поле.
Аналогично потоку вектора напряженности поля (4.7) применяется понятие потока вектора электрического смешения.
Поток вектора смещения ND в однородном поле равен произведению численного значения вектора смещения D и площадки S, во всех точках которой вектор смещения имеет одинаковое значение и направлен перпендикулярно к ней, т. е.
При неоднородном поле произвольную поверхность площадью S разбивают на элементарные, в пределах каждой на которых смещение одинаково; так что поток вектора
смещения через такую элементарную площадку
где Dn— нормальная составляющая вектора смещения (перпендикулярная к элементарной площадке).
Поток вектора смещения через произвольную замкнутую поверхность находится суммированием элементарных потоков: 
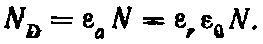
В частности, в случае шаровой поверхности
Таким образом, поток вектора электрического смещения через шаровую поверхность равен заряду, расположенному внутри поверхности.
Полученное выражение ND = Q справедливо для замкнутой поверхности любой формы, охватывающей заряд как в однородной среде с εr = const, так и в среде, диэлектрическая проницаемость которой неодинакова в различных участках среды, например в двухслойном конденсаторе.
На поверхности шара,
откуда определяется электрическое смещение у поверхности шара: что согласуется с (5).
Видео:44. Электрическое поле в диэлектрике. Вектор поляризованностиСкачать

Вектор электрического смещения
Электрическое поле графически изображается системой линий напряженности. На границе раздела двух диэлектриков количество линий напряженности изменяется: часть их заканчивается или начинается на связанных зарядах (рис. 47.1). По этой причине для описания поля в неоднородных диэлектриках используется вспомогательная величина – вектор электрического смещения

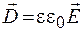
Направление вектора смещения в изотропной среде совпадает с направлением вектора напряженности. Линии вектора смещения непрерывны на границе раздела различных диэлектриков (рис. 47.2).
Объединяя выражения (47.1) и (29.2), для поля плоского конденсатора получаем
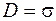
Следовательно, единицей вектора электрического смещения является кулон на метр в квадрате 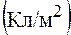
Поток вектора электрического смещения через поверхность S определяется формулой
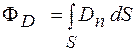
Из выражения теоремы Гаусса для напряженности электрического поля можно получить соответству-ющее выражение для вектора электрического смещения. Умножив обе части уравнения (26.7) на 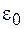
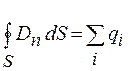
Поток вектора электрического смещения через произвольную замкнутую поверхность равен алгебраической сумме зарядов, находящихся внутри этой поверхности.
Для установления связи между вектором электрического смещения и поляризованностью диэлектрика подставим выражение (46.7) в уравнение (47.1):
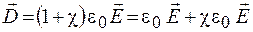
Учитывая выражение (45.3), формулу (47.5) приводим к виду
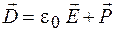
В вакууме (практически и в воздухе) 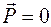
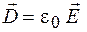
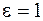
Таким образом, для описания электрических полей кроме напряженности 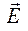


Дата добавления: 2015-08-08 ; просмотров: 5888 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
🎥 Видео
45. Электрическое смещениеСкачать

Что такое "ток смещения"?Скачать

Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Лекция 237. Вектор электрической индукцииСкачать

Билет №31 "Ток смещения"Скачать

Урок 383. Вихревое электрическое поле. Ток смещенияСкачать

Урок 238. Емкость плоского конденсатора. Классификация конденсаторовСкачать

Лекция №4 "Диэлектрики, вектор электрической индукции"Скачать

Вектор Пойнтинга и энергия конденсатораСкачать

Билет №02 "Теорема Гаусса"Скачать

Урок 228. Диэлектрики в электрическом поле. Диэлектрическая проницаемостьСкачать

Уравнения Максвелла. Вихревое электрическое поле. Ток смещенияСкачать

Лекция №20 "Ток смещения в диэлектрике. Квазистационарные явления"Скачать

Электрон в конденсаторе уч 10 кл упр 182Скачать

5. Конденсаторы. Магнитное поле в диэлектрикахСкачать

Электричество и магнетизм - Лекция 4Скачать

ЗАДАЧА на электростатическое поле │Расчет плоского конденсатора │Уравнение ПуассонаСкачать

Диэлектрик в электрическом полеСкачать