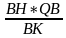Задачи егэ на вневписанную окружность

Данная работа будетет интересна ученикам,желающим изучить теорию и научиться решать задачи на вневписанную окружность.Учителя могут применять данный материал при объяснении и отработке данной темы.

Видео:Вневписанная окружностьСкачать

Скачать:

Предварительный просмотр:

Видео:Это будет на ЕГЭ 2020 по математике. Вписанная и вневписанная окружности.Скачать

Подписи к слайдам:

Электронное пособие по теме : «Вневписанная окружность» .

Содержание: 1. Определение вневписанной окружности. Основные теоремы и формулы. Определение вневписанной окружности. Центр вневписанной окружности. Касательная к вневписанной окружности. Радиус вневписанной окружности: Соотношение между радиусом вневписанной окружности и периметром треугольника. Соотношение между радиусом вневписанной окружности, площадью и периметром треугольника. Задачи : Задача №1. Задача №2. Задача №3. 2. Соотношения с радиусами вневписанных окружностей. Выражение суммы радиусов вневписанных окружностей через радиус вписанной окружности и радиус описанной окружности. Выражение суммы величин, обратных радиусам вневписанных окружностей, через величину обратную радиусу вписанных окружностей. Выражение суммы всех попарных произведений радиусов вневписанных окружностей через квадрат полупериметра треугольника. Выражение произведения радиусов вневписанных окружностей через произведение радиуса вписанной окружности и квадрат полупериметра треугольника. + следствие №1. следствие №2. Задачи : Задача №4. Задача №5. Задача №6. Задача №7.

1. Определение вневписанной окружности. Основные теоремы и формулы.

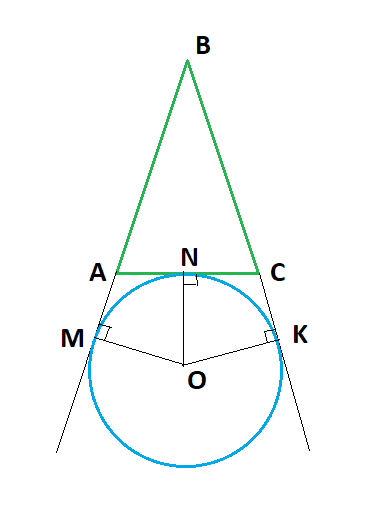
Вневписанная окружность. Окружность называется вневписанной для треугольника, если она касается одной стороны треугольника и продолжений двух других сторон. Для каждого треугольника существует три вневписанных окружности, которые расположены вне треугольника, почему они и получили название вневписанных . О 3 O 2 О 1

Центр вневписанной окружности. Центр вневписанной окружности треугольника — точка пересечения биссектрисы внутреннего угла треугольника, противолежащего той стороне треугольника, которой окружность касается, и биссектрис двух внешних углов треугольника. . А В С O

Дано:  ABC ; Вневписанная окр. (О а ; r а ) Доказать: Док-во: Т.к. касательные, проведенные из одной точки, равны ,то ВВ 1 =ВА 1 , СА 1 =СС 1 , АВ 1 =АС 1 . Значит, P = (АС+СА 1 )+(АВ+ВА 1 )= (АС+СС 1 )+(АВ+ВВ 1 )= АС 1 +АВ 1 =2АС 1 =2АВ 1 , т.е. Расстояние от вершины угла треугольника до точек касания вневписанной окружности со сторонами этого угла равны полупериметру данного треугольника

Дано:  ABC ; Вневписанная окр. (О а ; r а ) Доказать: Док-во: В прямоугольном треугольнике  АО а С 1 r a и – длины катетов, О а АС = , поэтому , что и требовалось доказать. II . Радиус вневписанной окружности, касающейся сторон данного внутреннего угла треугольника, равен произведению полупериметра треугольника на тангенс половины этого угла, т. е.

III . Радиус вневписанной окружности, касающейся данной стороны треугольника, равен отношению площади треугольника к разности полупериметра и этой стороны. т.е. Дано:  ABC ; Вневписанная окр. (О а ; r а ) Доказать: Док-во: Имеем: , что и требовалось доказать. А В С О а В 1 С 1 b c r a r a r a а

Задачи на свойства касательной к вневписанной окружности и ее радиусов:

Задача№1. Найдите периметр треугольника АВС, если расстояние от вершины А до точки касания с вневписанной окружностью равно 17 , расстояние от вершины B до точки касания окружности со стороной BC равно 6, расстояние от вершины С до точки касания окружности со стороной АC равно 4. (авторская задача) Решение

Решение №2: 1) Т.к АВ 1 = АС 1 = ( по теореме о касательной вневписанной окружности) , то Р= АВ 1 * 2 => Р= 17*2=34. Ответ: Р = 34. Решение: Дано: Окр(О а ;О а C 1 );  АВС;AB 1 =17, BL =6, CC 1 =4. Найти: P -?. Решение №1: 1) Рассмотрим  АВС. Т.к. BL=BB 1 =6 (как отрезки касательных, проведенные из одной точки), то АВ=АВ 1 — BB 1 => АВ =17-6 =11 . 17 А В В 1 О а L 6 4 С С 1 2) Т.к. СL=СB 1 =4 (как отрезки касательных, проведенные из одной точки), то ВС=BL + LC => В C =6+4 =10 . 4) Р=AB+ВС+АС => Р=11+10+13=34 . 3) Т.к. AB 1 =АС 1 =17 (как отрезки касательных, проведенные из одной точки), то АС= АС 1 — CC 1 => АС =17-4 =13 . 13

Задача№2. Решение Задача№2. Найдите радиус вневписанной окружности треугольника со сторонами 13, 13, 10. ( ЕГЭ- 2015, система задач по геометрии Р.К.Гордина)

Решение 1 : Дано: Окр(О а ; r а );  АВС;AB=1 3 , AC = 13 , BC=10 . Найти: r а -?. Решение (1 случай) : 1 . Пусть стороны AB , AC и BC треугольника ABC равны 13, 13 и 10 соответственно, AH — высота треугольника, r a — радиус вневписанной окружности, касающейся сторон BC , AC и AB — в точках H , K и M соответственно. А В С M H О а r a 5 5 5 13 13 12 18 K 2.Поскольку  АВС равнобедренный, точка H — высота и середина основания BC. Рассмотрим  А H В, где  H=90  . По теореме Пифагора: 3. Пусть O a — центр вневписанной окружности, касающейся стороны BC и продолжения сторон AC и AB, причём продолжения стороны AB —в точке M. Тогда BM = BH = 5 (как отрезки касательных, проведенные из одной точки) ; AM = AB + BM = 13 + 5 = 18. 4. Рассмотрим  А MO a , где  M=90  (т еорема о касательной к окружности ). По теореме радиусе вневписанной окружности получаем, что ( AM= по теореме о расстоянии от вершины угла треугольника до точек касания с вневписанной окружности )

Решение 2 : Дано: Окр(О c ; r c );  АВС;AB=1 3 , AC = 13 , BC=10 . Найти: r c -?. Решение (2 случай): 1 . Пусть O c — центр вневписанной окружности, касающейся стороны AB и продолжений сторон BC и AC в точках K и L соответственно. Тогда AO —биссектриса  BAL, а так как AH — биссектриса смежного с ним  BAC, то ∠ HAO c = 90  . А В С L H О c r c 5 5 13 12 K 2. Четырёхугольник AO c KH — прямоугольник (∠ HAO c = ∠AHK = ∠HKO c = 90  ), поэтому r c = O c K = AH = 12 . 3. Аналогично найдём, что r b = AH = 12. Ответ: r a = 7,5; r b = 12 ; r c = 12 . 12

Задача№3. Найдите радиус вневписанной окружности, если расстояние от вершины А до точки касания с окружностью равно 21, BC=15, AB=14,AC=13. (авторская задача) Решение

Дано: AB 1 =21, AB=14, AC=13, BC=15. Найти: r a -? . Решение : O A C C 1 L 1 5 1 3 B 21 1 4 B 1 1 ) Рассмотрим  ABC : 2 ) 3) По теореме о радиусе вневписанной окружности:  ( по формуле Герона) ( по теореме о касательной к вневписанной окружности) Ответ: r a = 14 . r a r a Решение:

2. Соотношения с радиусами вневписанных окружностей.

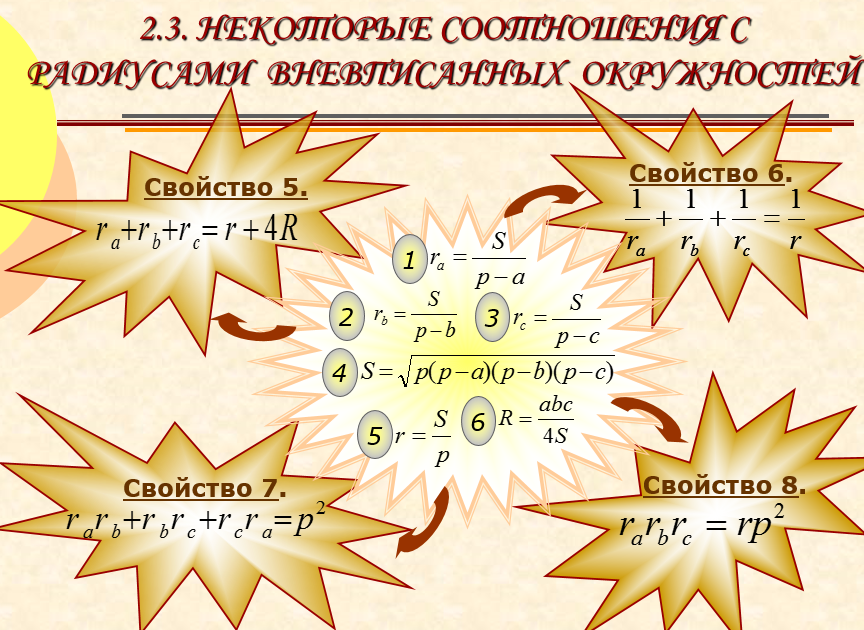
Выражение суммы радиусов вневписанных окружностей через радиус вписанной окружности и радиус описанной окружности . Дано:  ABC ; Вневписанная окр. (О а ; r а ), (О b ; r b ), (О c ; r c ), вписанная окр .(О; r ), описанная окр.(О; R). Доказать: Док-во: Выразим все радиусы через стороны, S и полупериметр треугольника: Значит,  поскольку радиус описанной окружности удовлетворяет равенству , то справедлива формула ,что и требовалось доказать. О c О b О a О О r c r b r a r R a b c

Выражение суммы величин , обратных радиусам вневписанных окружностей , через величину обратную радиусу вписанных окружностей . Выражение суммы всех попарных произведений радиусов вневписанных окружностей через квадрат полупериметра треугольника.

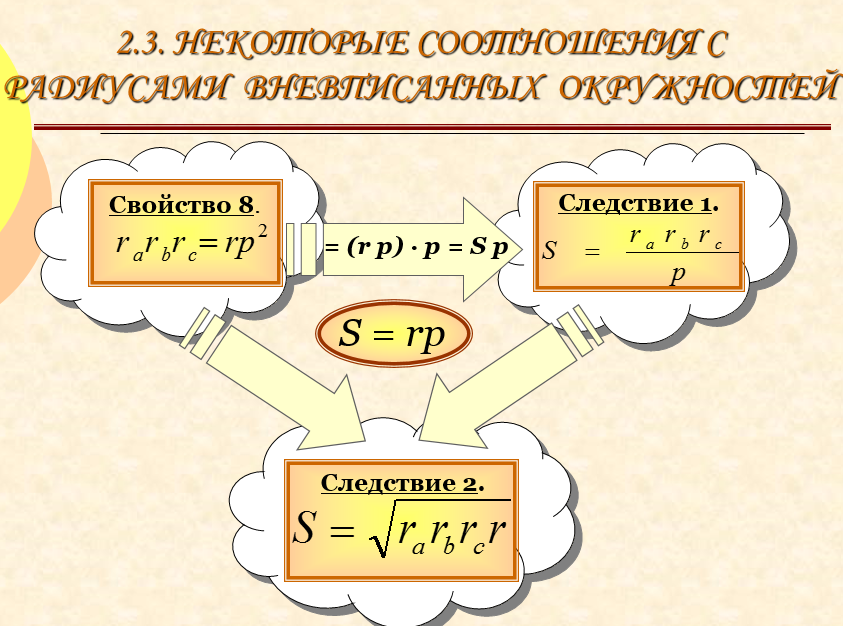
Выражение произведения радиусов вневписанных окружностей через произведение радиуса вписанной окружности и квадрат полупериметра треугольника . Дано:  ABC ; Вневписанная окр. (О а ; r а ), (О b ; r b ), (О c ; r c ) , вписанная окр.(О; r). Доказать: Док-во: Из ранее доказанных формул для радиусов и формулы Герона Тогда , что и требовалось доказать. Следствия r a r c r b О c О b О а В A r C О

1 следствие: Площадь треугольника равна отношению произведения всех трех радиусов вневписанных окружностей к полупериметру треугольника. Дано:  ABC ; Вневписанная окр. (Оа; r а ), (О b ; r b ), (О c ; r c ) . Доказать: Док-во : Из Следовательно , что и требовалось доказать. О c r c В r a О а C r b О b A

2 следствие: Площадь треугольника равна квадратному корню из произведения всех трех радиусов вневписанных окружностей и радиуса вписанной окружности. Дано:  ABC ; Вневписанная окр. (Оа; r а ), (О b ; r b ), (О c ; r c ) вписанная окр.(О; r). Доказать: Док-во : Из следствия 1 , что и равенства, получаем, перемножая их почленно, . Значит, , что и требовалось доказать. О c r c В r a О а C r b О b A О r

Задачи на соотношения с радиусов вневписанных окружностей:

Задачи: Задача№4. Найдите радиус вневписанной окружности треугольника, если радиусы двух других вневписанных окружностей равны 2002 и 4004, а радиус вписанной окружности равен 1001. Решение

Решение: Дано:  ABC ; Окр(О; r х =1001), Окр(О 3 , r с ), Окр(О 1 ; r а =2002), Окр(О 2 ;r b =4004). Найти: r с -? O 3 O 2 O O 1 r a r c r b r x 2002 1001 4004 ? C A В Т.к. сумма величин, обратных радиусам вневписанных окружностей, равна величине, обратной радиусу вписанной окружности, а именно , то c оставим равенство: Ответ: r с =4004 . Решение:

Задачи: Задача №5. Найдите произведение сторон треугольника, если известно, что радиусы его вневписанных окружностей равны 9,18 и 21. (сборник «Подготовка к ЕГЭ -2010, под редакцией Ф.Ф.Лысенко) Решение

Решение: Дано:  ABC ; r a =9, r b =18, r c =21 ; Окр(О, r с ), Окр(О; r а ), Окр(О; r b), Окр(О; R ) . Найти: , следовательно r a r b r c O O O O R r О 1. Найдем S : , получаем 2. Найдем 4 R : Подставляем: Ответ: 5460. Решение:

Задачи: Задача №6. Найдите произведение радиусов всех вневписанных окружностей треугольника со сторонами 4,5,6. (сборник «Подготовка к ЕГЭ- 2010, под редакцией Ф.Ф.Лысенко) Решение

Решение: Дано:  ABC ; a= 4 , b= 5 , c= 6; Окр(О, r с ), Окр(О; r а ), Окр(О; r b) Найти: 2. Так как , то Таким образом, Ответ: a (4) c (6) b (5) O O O r a r b r c O r 1. Так как , где r -радиус вписанной в треугольник окружности, то: Решение:

Задачи: Задача№7. Основание АС равнобедренного треугольника равно 10. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания АС в его середине. Найдите радиус окружности вписанной в треугольник АВС. (сборник «Подготовка к ГИА -2013, под редакцией Д.А. Мальцева) Решение

3. АК – высота, проведенная к гипотенузе  AK²=FK*KO ( по теореме о высоте прямоугольного )  Так как FK – радиус вписанной в  АВС окружности, следовательно Ответ: Решение: Дано:  ABC -равнобедренный; AC = 10; вписанная окр.( F ; r), вневписанная о кр.(О; r а= 7,5 ). Найти: r- ? 1 . Так как окружность касается стороны треугольника и продолжения двух других сторон, то это — вневписанная окружность. F O А B C K r r a 2. Так как центр вписанной окружности и вневписанной окружности лежит в точке пересечения биссектрис, то AF-биссектриса  ВАС, а AO – биссектриса  CAD   FAO – прямоугольный треугольник, так как биссектрисы смежных углов образуют прямой угол. D Решение:

Видео:Задача про две вневписанные окружности | ЕГЭ. Задание 16. Математика | Борис Трушин |Скачать

«Системный подход к обучению решению геометрических задач с вневписанными окружностями при подготовке к ОГЭ и ЕГЭ»

Эта разработка поможет учителям и учащимся при решении сложных задач (ОГЭ №26 и ЕГЭ №16 по планеметрии на вневписанные окружности, а также при проведении элективных курсов в 9,11 классах.

Просмотр содержимого документа
««Системный подход к обучению решению геометрических задач с вневписанными окружностями при подготовке к ОГЭ и ЕГЭ»»

«Геометрические задачи с вневписанными окружностями при подготовке к ОГЭ и ЕГЭ»

(ОГЭ, задание №26, ЕГЭ, задание №16)

Подготовила слушатель курсов повышения

квалификации ГАУ ДПО БИПКРО

«Современный урок в логике ФГОС»

Коростина И.С., учитель математики

МБОУ «Гимназия №7 имени Героя

России С.В.Василева» г. Брянска

Задачи на данную тему представлены на экзаменах в 9-х и 11-х классах. При их решении выпускники испытывают наибольшие затруднения. Многие из них даже не приступают к решению. Данная тема выходит за рамки школьной программы. В большей части заданий термин «вневписанная окружность» не фигурирует, а появляется как вспомогательная фигура, именно, поэтому знание свойств вневписанной окружности помогает решать различные геометрические задачи.

Окружность называют окружностью, вневписанной в треугольник, или вневписанной окружностью, если она касается одной стороны треугольника и продолжений двух других сторон.

Для каждого треугольника существует три вневписанных окружности, которые расположены вне треугольника, почему они и получили название вневписанных.

Подготовительные задачи на свойства вневписанной окружности.

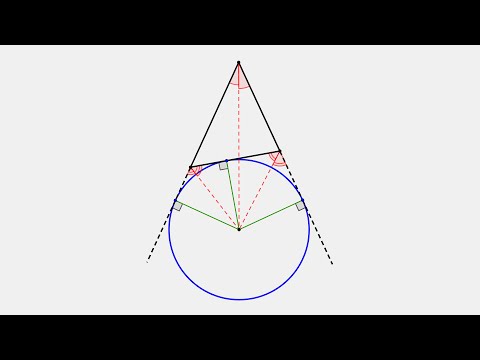
З адача 1. Дан ABC. Центры вневписанных окружностей O₁, O₂ и O₃ соединены прямыми. Доказать, что O₁O₂O₃ — остроугольный.

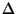
Решение: Центр O₁ вневписанной окружности, касающейся стороны BC, является точкой пересечения биссектрис внешних углов при вершинах B и C. Поэтому

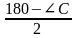
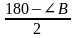
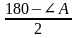
∠O₁CB = и ∠ O₁BC = . Следовательно, ∠BO₁C = o .

Задача 2. Докажите, что прямая, проходящая через центры вневписанных окружностей треугольника ABC, касающихся сторон AB и AC, перпендикулярна прямой, проходящей через центр вписанной окружности и вершину A.

Решение: Пусть O₁ и O₂ – центры вневписанных окружностей треугольника ABC, касающихся сторон AB и AC соответственно; O — центр вписанной окружности треугольника ABC. Поскольку точкиO₁ и O₂ расположены на биссектрисах вертикальных углов с вершиной A, то прямая O₁O₂ проходит через точку A.∠ O₁AO – это угол между биссектрисами смежных углов, поэтому ∠O₁AO = 90°.

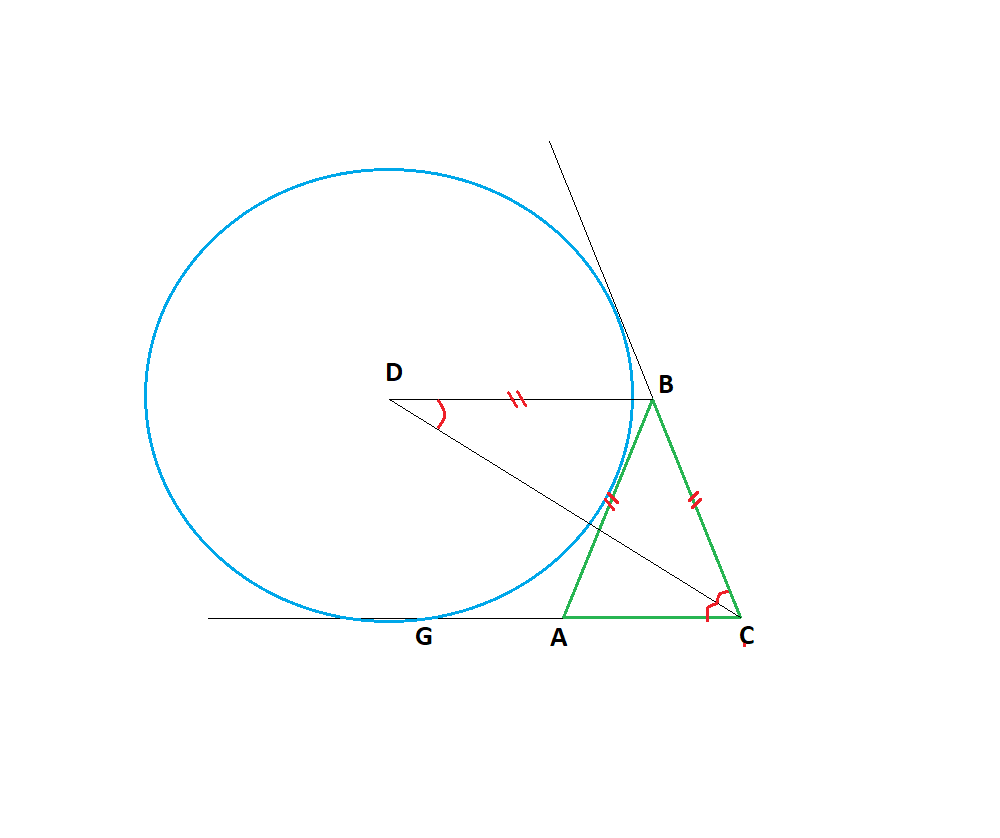
Задача 3. Дан равнобедренный треугольник ABC с основанием AC. Доказать, что конец D отрезка BD, выходящего из вершины B, параллельного основанию и равного боковой стороне треугольника, является центром вневписанной окружности треугольника.

Решение: BD – биссектриса внешнего угла ∠B. Треугольник CBD – равнобедренный, поэтому ∠GCD = ∠BDC = ∠DCB (G – точка на продолжении отрезка AC за точку C), то есть CD – биссектриса ∠C. D –точка пересечения биссектрис BD и CD, она, как известно, является центром вневписанной окружности.

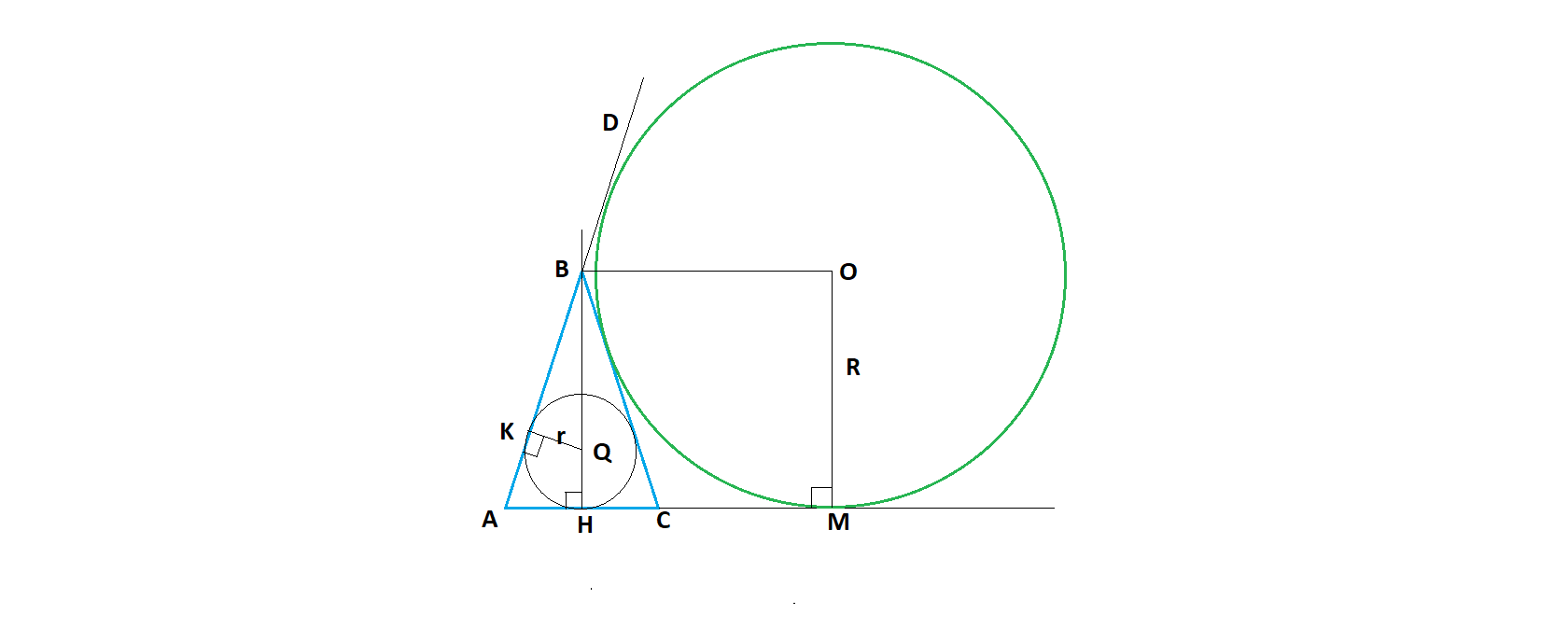
Задача 4. Вневписанная окружность равнобедренного треугольника касается его боковой стороны. а) Докажите, что радиус этой окружности равен высоте треугольника, опущенной на основание. б) Известно, что радиус этой окружности в 4 раза больше радиуса вписанной окружности треугольника. В каком отношении точка касания вписанной окружности с боковой стороной треугольника делит эту сторону?

а) Вневписанной окружностью называется окружность, которая касается стороны треугольника и продолжений двух других его сторон. Пусть ∠А = ∠С = α, так как треугольника ∆АВС — равнобедренный. ∠DBC – внешний угол треугольника ∆АВС, поэтому ∠DBC = ∠А + ∠С = 2α. Окружность касается сторон угла ∠DBC, значит, ВО – биссектриса угла ∠DBC, т. е. угол ∠DBО = ∠ОBC = α. Получаем, что ∠DBО = ∠А = α. Соответственные углы ∠DBО и ∠А при пересечении прямых ВО и АМ секущей AD равны, то прямые ВО и АМ параллельны. BH – высота треугольника ∆АВС, следовательно, BH перпендикулярна АМ. АМ – касательная к окружности, следовательно, ОМ перпендикулярна АМ (ОМ – радиус окружности). Значит, ВН || ОМ. Получаем, ВОМН – прямоугольник. Следовательно, радиус окружности равен высоте треугольника, опущенной на основании, т. е. R = BH.

б) Пусть радиус вневписанной окружности ОМ = R, а радиус вписанной в треугольник окружности QK = QH = r. Тогда по условию R = 4r. Треугольники ∆АВН и ∆QВК – подобные треугольники (∠В – общий, ∠ВКQ = ∠ВНА), следовательно,

AB=

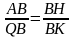
BH = OM = R = 4rQB = BH – QH = 4r – r = 3r

Из прямоугольного треугольника ∆QBK по теореме Пифагора найдем BK:

BK 2 = QB 2 – KQ 2= (3r) 2 – r 2 = 8 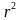. BK = 2√2r.

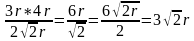
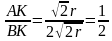
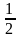
AB= AK = AB – BK=3√2r – 2√2r = √2r. Тогда отношение, в котором точка касания вписанной окружности с боковой стороной треугольника делит эту сторону, равно Ответ: .

Задача 5 . Найдите периметр треугольника ABC, если расстояние от вершины A до точки касания с вневписанной окружностью равно 17, расстояние от вершины B до точки касания окружности со стороной BC равно 6, расстояние от вершины C до точки касания окружности со стороной AC равно 4.

Р 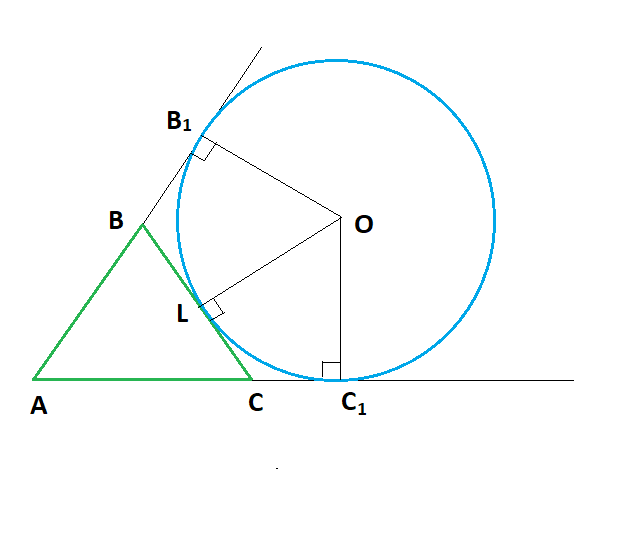ешение:

1)Рассмотрим

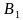
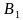
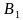
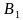
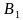
a)Т.к.BL=B =6 (как отрезки касательных, проведенных из одной точки), то AB=A -B =AB=17-6=11. b) Т.к. CL=C =4 (как отрезки касательных, проведенных из одной точки), то BC=BL+LC =BC=6+4=10.c)Т.к. A =A =17(как отрезки касательный, проведенных из одной точки), то AC=A -C =AC=17-4=13

2) P=AB+BC+AC = P=11+10+13=34 Ответ: 34.

Задача 6. Найдите радиус вневписанной окружности треугольника, если радиусы двух других вневписанных окружностей равны 2002 и 4004, а радиус вписанной окружности равен 1001.

Т .к. сумма величин обратных радиусам вневписанных окружностей, равна величине, обратной радиусу вписанной окружности, а именно

, то составим равенство: =

Задачи для самостоятельного решения.

Задача 1. Вневписанная окружность касается боковой стороны равнобедренного треугольника АВС. Доказать, что высота треугольника АВС, опущенная на основание, равна радиусу вневписанной окружности. В каком отношении точка касания вписанной в треугольник АВС окружности делит его сторону ВС, если радиус, вписанной в треугольник АВС окружности в 4 раза меньше радиуса вневписанной окружности. (Задача №16 ЕГЭ 2016г.) Ответ:1:2.

Задача 2. Вневписанная окружность равнобедренного треугольника касается его боковой стороны.

а) Докажите, что радиус этой окружности равен высоте треугольника, опущенной на основание. б) Известно, что радиус этой окружности в 4 раза больше радиуса вписанной окружности треугольника. В каком отношении точка касания вписанной окружности с боковой стороной треугольника делит эту сторону? (Задача №16 ЕГЭ 2016г.) Ответ: .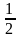

Задача 3. Дана трапеция АВСD, основания которой ВС=44, АD=100, АВ=СD=35. Окружность касается прямых АD и ВС, касается стороны СD в точке К. а)Докажите, что Ас=75. б)Найдите длину отрезка СК.(20 вариантов текстов ЕГЭ 2019Ященко. Тематическая рабочая тетрадь. Диагностическая работа №2. Задача № 16). Ответ 5 или 30.

Задача 4. Основание АС равнобедренного треугольника равно 10. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания АС в его середине. Найдите радиус окружности вписанной в треугольник АВС. (сборник «Подготовка к ГИА-2013, под редакцией Д.А. Мальцева) Ответ: 10/3.

Задача 5. Точка О ₁ — центр вписанной окружности треугольника АВС, а точка О ₂ – центр окружности, касающейся стороны ВС и продолжений сторон АВ и АС. Найдите расстояние между точками О ₁ и О ₂ , если радиус описанной окружности треугольника АВС равен 6, а sin 1С = √5/3. ( Сборник « Математика. Все для ЕГЭ 2011». Часть I. Автор Д. А. Мальцев). Ответ: 16.

Задача 6. В равнобедренном треугольнике ABC основанием AB = 24 длины боковых сторон равны 37. Найдите радиус окружности, касающейся стороны AB и продолжений сторон AC, BC за точки A и B соответственно. (сборник «Подготовка к ОГЭ-2019, под редакцией Д.А. Мальцева). Ответ: 16,8.

Задача 7. К окружности, вписанной в равнобедренный треугольник ABC, проведена касательная , которая параллельна основанию AB и пересекает боковые стороны AC, BC в точках M и N соответственно. Найдите площадь треугольника ABC, если MN = 20, CM = 26. (сборник «Подготовка к ОГЭ-2019, под редакцией Д.А. Мальцева) Ответ: 1215.

Задача 8. Найдите произведение радиусов всех вневписанных окружностей треугольника со сторонами 4,5,6.(сборник «Подготовка к ЕГЭ-2010, под редакцией Ф.Ф.Лысенко) Ответ:225 √7 /8.

Задача 9. Найдите произведение сторон треугольника, если известно, что радиусы его вневписанных окружностей равны 9,18 и 21. .(сборник «Подготовка к ЕГЭ-2010, под редакцией Ф.Ф.Лысенко). Ответ: 5460 .

Задача 10. Найдите радиус вневписанной окружности треугольника со сторонами 13, 13, 10. (ЕГЭ-2015, система задач по геометрии Р.К.Гордина) Ответ: r_a = 7,5; r_b = 12; r_c = 12.

Задача 11. Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка М. Окружность с центром О и диаметром СМ касается гипотенузы в точке N.

а) Докажите, что MN и ВО параллельны.
б) Найдите площадь четырёхугольника BOMN, если СN=4 и АМ : МС как 1:3.

(вариант 36, Ященко 36 вариантов, ЕГЭ-2018). Ответ:7.

Задача 12. Две касающиеся внешним образом в точке К окружности, радиусы которых равны 22 и 33, касаются сторон угла с вершиной А . Общая касательная к этим окружностям, проходящая через точку К, пересекает стороны угла в точках В и С. Найдите радиус окружности, описанной около треугольника АВС. (вариант 3, Ященко 36 вариантов, ЕГЭ-2015). Ответ:68,75.

Задача 13. Окружности радиусов 12 и 52 касаются внешним образом. Точки А и В лежат на первой окружности , точки С и D — на второй . При этом АС и ВD — общие касательные окружностей . Найдите расстояние между прямыми АВ и СD . (вариант 17, Ященко 36 вариантов, ЕГЭ-2015). Ответ:39.

Задача 14 . Радиусы двух вневписанных окружностей прямоугольного треугольника равны 7 и 23. Найдите расстояние между их центрами. (ЕГЭ — 2015. С.4).Ответ: 34 или 30 .

Задача 15 . В окружность с центром в точке О вписан прямоугольный треугольник АВС с гипотенузой АВ. На большем катете ВС взята точка D так, что АС=ВD. Точка Е – середина дуги АСВ.

а) Докажите, что угол СЕD= 90 0.

б) Найдите площадь пятиугольника АО D ЕС, если известно, что АВ=13, АС = 5.

(Тренировочные работы №6, т/р №167 А.Ларина). Ответ: 36.

Видео:ТОП-3 конструкции с окружностями для №16 из ЕГЭ 2023 по математикеСкачать

ЕГЭ, С4 (№18). Вневписанные окружности

В новом формате ЕГЭ по математике задание значится как «Задание №16»

Видео:№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

Видеоразбор

Продолжаем готовится к ЕГЭ по математике. Учимся решать задачи категории С4.

Две окружности, радиусы которых 9 и 4, касаются внешним образом. Найдите радиус третьей окружности, которая касается двух данных окружностей и их общей внешней касательной

Чтобы не потерять страничку, вы можете сохранить ее у себя:

🎥 Видео

✓ Как вневписанная окружность Герону помогла | Ботай со мной #083 | Борис ТрушинСкачать

Вневписанная окружностьСкачать

✓ За 1 минуту научимся решать задачи на совместное движение по кругу | ЕГЭ. Задание 9 | Борис ТрушинСкачать

Вся геометрия треугольника в одной задаче. Планиметрия. ЕГЭ 2023 математика задача 16Скачать

ВСЯ ГЕОМЕТРИЯ ИЗ ОГЭ ПО МАТЕМАТИКЕ 2023 ЗА 40 МИНУТСкачать

Вневписанная окружность. Практика. Задача из Ященко | Профильная математика в онлайн - школе СОТКАСкачать

[11] Окружности с нуля для ЕГЭ по математике. Вневписанная окружность Теория и практика 13 задач.Скачать

ВНЕвписанная окружность. Решение задач. 16 задание ЕГЭ профильная математикаСкачать

Все типы 1 задание ЕГЭ по математике профиль 2024Скачать

Все об окружностях на ЕГЭ | Профильная математика 2023 | УмскулСкачать

✓ Неравенство, которое вынесло почти всех | ЕГЭ-2018. Задание 15. Математика. Профиль | Борис ТрушинСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

ЕГЭ-2020. №16. Вневписанная окружность🚀 Ортоцентр. Теорема Карно, Бланшета, Чевы, Менелая🔥Скачать

Разбор задачи 16 про вневписанные окружности. Геометрия. ЕГЭ 2019Скачать

✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать