Закрепленные и свободные вектора (8 видео)

Закрепленные и свободные вектора

§ 1. Определения свободного и закрепленного геометрических векторов.

Определение 1: Закрепленный вектор – отрезок с упорядоченными концами: AB,

A – начало вектора, В – конец вектора, АВ ≠ ВА.

Конец и начало вектора могут совпадать: АА – нулевой вектор.

Определение 2: Равенство закрепленных векторов:

Пусть AB и CD – закрепленные ненулевые векторы.

1) Соединим А с С и В с D (начальные и конечные точки векторов).

Если ABDC – параллелограмм, то AB = CD.

2) AB = CD, если 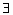закрепленный вектор EF : AB = EF и EF = CD.

3) Все нулевые векторы равны: АА = ВВ.

Определение 3: Свободный вектор (или просто вектор) – множество равных между собой (в смысле определения 2) закрепленных векторов.

Свободные векторы обозначаются прописными латинскими буквами – a .

Нулевой свободный вектор обозначается θ .

Определение 4: Закрепленный вектор AB является реализацией свободного вектора a , если a = ( То есть свободный вектор a – это множество закрепленных векторов CD, т.ч. CD = AB. )

Обозначение : AB 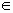a (допустимо а = АВ).

Предложение 1. с.в. а и т. О пространства ! з.в. ОА : ОА а .

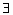
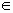
( Т.е. для любого свободного вектора a и для любой точки О пространства существует единственный закреплённый вектор OA, который является реализацией а . )

Определение 5: Длина свободного вектора a – это длина его реализации:

| a | = |AB|, если AB 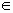a , | θ | = 0.

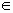
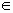
Определение 6: Угол между свободными векторами а и b – это наименьший угол между их реализациями ОА и ОВ ( ОА а , ОВ b ).

Определение 7: Свободные векторы a и b равны ( a = b ), если они совпадают как множества.

Из определения свободного вектора очевидно, что для того, чтобы задать свободный вектор a, достаточно задать какую-либо его реализацию, т.е. закрепленный вектор AB 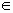a .

Определение 8: V 3 – множество всех свободных векторов в пространстве R 3 .

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Содержание

Элементы векторной алгебры. Понятия связанного и свободного векторов
Понятия связанного и свободного векторов
Линейные операции над векторами
Знакомимся с вектором
Линейная алгебра
Что такое вектор
Как записывать
Скаляр
Как изображать
И зачем нам это всё
Что дальше
💥 Видео

Видео:Собственные векторы и собственные числа линейного оператораСкачать

Элементы векторной алгебры. Понятия связанного и свободного векторов

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

Рассмотрим две точки А и В. По соединяющему их отрезку можно перемешаться в любом из двух противоположных направлений. Если считать, например, точку А начальной, а точку В конечной, то тогда получаем направленный отрезок АВ, в другом случае — направленный отрезок В А. Направленные отрезки часто называют связанными или закрещенными векторами.

На чертеже заданное направление указывается стрелкой (рис. 1). Рис.3 Рис. 1 В случае, когда начальная и конечная точки совпадают, А = В, связанный вектор называется нулевым. Определение. Будем говорить, что связанные векторы АВ и CD равны, если середины отрезков AD и ВС совпадают (рис.2). Обозначение: А В = CD. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ.

Понятия связанного и свободного векторов

Линейные операции над векторами. Умножение вектора на число Заметим, что в случае, когда точки А, В, С и D не лежат на одной прямой, это равносильно тому, что четырехугольник ABCD — параллелограмм. Ясно, что равные связанные векторы имеют равные длины. Пример. Рассмотрим квадрат и выберем векторы, как указано на рис.3. Векторы АВ и DC равны, а векторы ВС и DA не равны, р Укажем некоторые свойства равных связанных векторов: 1.

Каждый связанный вектор равен самому себе: АВ = АВ. Если Пусть АВ — заданный связанный вектор и С — произвольная точка. Ясно, что, опираясь на определение, всегда можно построить точку D так, чтобы CD = АВ. Тем самым, от каждой точки можно отложить связанный вектор, равный исходному (рис.5). Мы будем рассматривать свободные векторы, т. е. такие векторы, начальную точку которых можно выбирать произвольно, или, что то же самое, которые можно произвольно переносить параллельно самим себе.

Ясно, что свободный вектор А В однозначно определяется заданием связанного вектора АВ. Если в качестве начальных выбирать лишь те точки, которые лежат на прямой, определяемой заданным (ненулевым) связанным вектором, то мы приходим к понятию скользящего вектора (рис. 6). Рис. 6 Рис. 4 Связанные и скользящие векторы широко используются п теоретической механике.

Для обозначения свободных векторов будем пользоваться полужирными строчными латинскими буквами — а, Ь, с. ; нулевой вектор обозначается через 0.

Пусть заданы вектор а и точка А. Существует ровно одна точка В, для которой & АВ = а (рис.7). Операция построения связанного вектора АВ, для кото- РИС 7 рого выполняется это равенство, называется откладыванием свободного вектора а от точки А. Заметим, что связанные векторы, получаемые в результате описанной операции откладывания,равнымеждусобойи,значит,имеютодинаковуюдлину. Этопозволяет ввести длину свободного вектора а, которую мы будем обозначать символом |а|.

Длина нулевого вектора равна нулю. Если а = Ь, то |а| = |Ь|; обратное неверно. §2. Линейные операции над векторами 2.1. Сложение векторов Пусть заданы два вектора а и Ь. Возьмем какую-нибудь точку О и отложим от нее вектор a: OA = а. От полученной точки А отложим вектор I»: АВ = Ь. Полученный в результате вектор оЪ называется суммой векторов а и b и обозначается через а + Ь (рис. 8). Этот способ построения суммы векторов называется правилом треугольника.

Нетрудно заметить, что сложение векторов коммутативно, т. е. для любых векторов а и b справедливо равенство (рис.9). Если отложить векторы а и I» от обшей точки О и построить на них как на сторонах параллелограмм, то вектор ОЙ, идущий из общего начала О в противоположную вершину параллелограмма, будет их суммой а + Ь (или b + а) (рис. 10). Этот способ построения суммы векторов называется правилом параллелограмма. Рис.9 Рис. ю ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ.

Линейные операции над векторами

Умножение вектора на число Пусть заданы три вектора, например, a, b и с. Отложим от произвольной точки О вектор a: OA = а; от полученной точки А отложим вектор b: АВ = Ь; отточки В — вектор с: ВС = с (рис. 11). По определению суммы оЪ = а + b и ОС = (а + Ь) + с (рис. 12). С другой стороны, ЛС = b + с и, значит, О? = а + (Ь + с) (рис. 13). Тем самым, для любых векторов a, b и с выполняется равенство т. е. сложение векторов ассоциативно. Опуская скобки, можно говорить о сумме трех векторов и записывать ее так: Рис. 12

Аналогично определяется сумма любого числа векторов: это есть вектор, который замыкает ломаную, построенную из заданных векторов. На рис. 14 показан», как построить сумму семи векторов: Приведенный способ сложения произвольного числа векторов называется правилом замыкающего ломаную. Пример. Найти сумму векторов, идущих из центра правильного шестиугольника в его вершины. По правилу замыкающего ломаную получаем (рис. 15). Рис. 15 2.2.

Возможно вам будут полезны данные страницы:

Умножение вектора на число Определение. Свободные векторы а и Ь называются коллинеарными, если определяющие их связанные векторы лежат на параллельных или на совпадающих прямых (рис. 16). Обозначение: а |) Ь. Замечание. И э определения следует, чтоесли хотя бы один из векторов а и Ь нулевой, то они коллинсарны. Если отложить К9ллинеарн1е векторы а и Ь от обшей точки О, OA = a, OB — I), то точки О, A w В будут лежать на одной прямой.

При этом возможны два случая: точки

А и Я располагаются на этой прямой: 1) по одну сторону от точки О, А 2) по разные стороны (рис. 17). В первом случае векторы а и b называются одинаково направленными, а во втором — противоположно направленными. Если векторы имеют равные длины и одинаково направлены, то они равны. Пусть а — вектор, Л — вещественное число.

Определение. Произведением вектора а на число А называется вектор 1> такой, что 2) векторы а и b одинаково (соответственно, противоположно) направлены, если А > 0 (соответственно, А 0). Обозначение: b = Аа. При Л = 0 положим Ла = О. Таким образом, векторы а и b = Аа коллинеарны по определению. Верной обратное: если векторы а (и Ф 0) и b коллинеарны, то можно найти число А такое, что 1х = Аа. Укажем основные свойства этой операции умножения вектора на число:

ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ. Понятия связанного и свободного векторов. Линейные операции над векторами. Умножение вектора на число (здесь А и ц — любые действительные числа, н и I) — произвольные векторы). Определение. Вектор, длина которого равна единице, называется единичным вектором, или ортом, и обозначается а0 (читается: а с нуликом), |а°| = 1. Если а Ф 0, то вектор есть единичный вектор (орт) направления вектора а (рис. 18).

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Свободные вектора. Линейные операции и их свойства. Векторное пространство как линейное.Скачать

Знакомимся с вектором

Основы линейной алгебры для тех, кого это миновало в универе.

Вы наверняка слышали много историй о программистах, которые учились в технических вузах, изучали высшую математику и теперь пользуются этими знаниями в программировании. И если кого-то это не коснулось, может быть ощущение, что он пропустил в жизни что-то важное.

Будем это исправлять. Попробуем разобрать некоторые базовые понятия из математики за пределами школьной программы. И заодно покажем, как оно связано с программированием и для каких задач полезно.

⚠️ Математики, помогайте. Мы тут многое упростили, поэтому будем рады увидеть ваши уточнения и замечания в комментариях.

Видео:Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

Линейная алгебра

Есть математика: она изучает абстрактные объекты и их взаимосвязи. Благодаря математике мы знаем, что если сложить два объекта с ещё двумя такими же объектами, то получится четыре объекта. И неважно, что это были за объекты: яблоки, козы или ракеты. Математика берёт наш вещественный мир и изучает его более абстрактные свойства.

Внутри математики есть алгебра: если совсем примитивно, то в алгебре мы вместо чисел начинаем подставлять буквы и изучать ещё более абстрактные свойства объектов.

Например, мы знаем, что если a + b = c , то a = c − b . Мы не знаем, что стоит на местах a, b или c, но для нас это такой абстрактный закон, который подтверждается практикой.

Внутри алгебры есть линейная алгебра — она изучает векторы, векторные пространства и другие абстрактные понятия, которые в целом относятся к некой упорядоченной информации. Например, координаты ракеты в космосе, биржевые котировки, расположение пикселей в изображении — всё это примеры упорядоченной информации, которую можно описывать векторами. И вот их изучает линейная алгебра.

В программировании линейная алгебра нужна в дата-сайенс, где из упорядоченной информации создаются алгоритмы машинного обучения.

Если представить линейную алгебру в виде дома, то вектор — это кирпич, из которого всё состоит. Сегодня разберёмся, что такое вектор и как его понимать.

Видео:Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

Что такое вектор

Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.

Физическое представление вектора: есть длина, направление и нет начальной точки отсчёта. Такой вектор можно как угодно двигать в пространстве

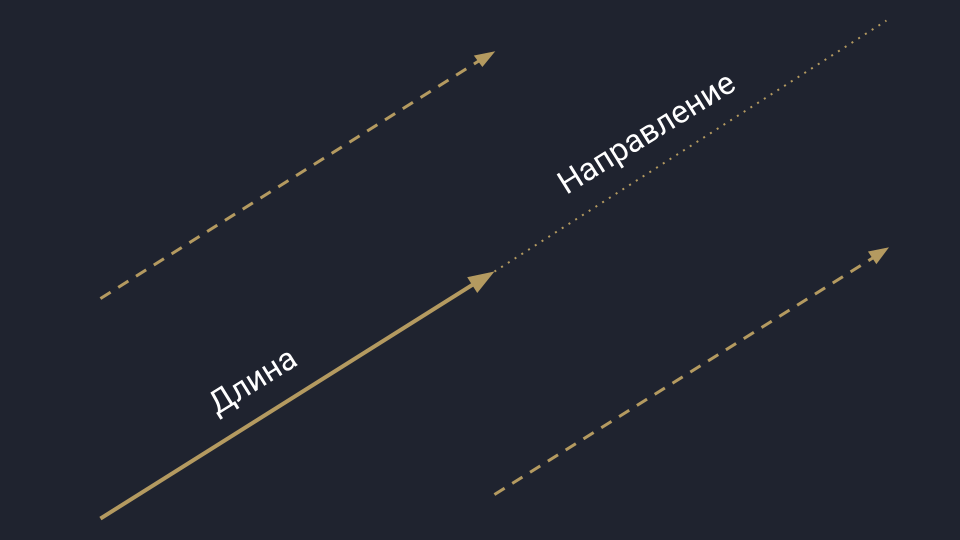
У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.

Аналитическое представление вектора: данные можно перевести в числа

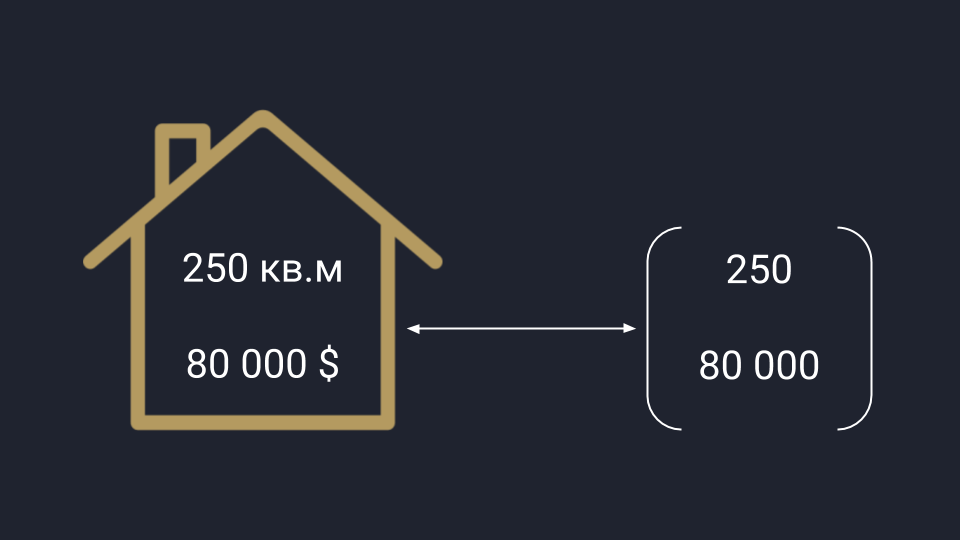
Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи. В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.

Математическое представление вектора: данные можно перевести в числа или график

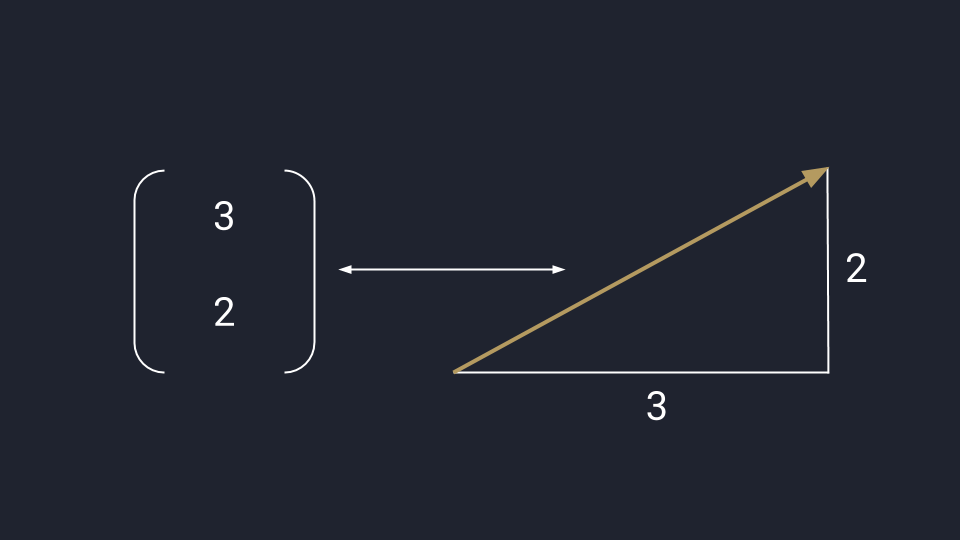
В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.

Векторная система координат с базовыми осями Х и Y. Место их пересечения — начало координат и корень любого вектора. Засечки на осях — это отрезки одной длины, которые мы будем использовать для определения векторных координат

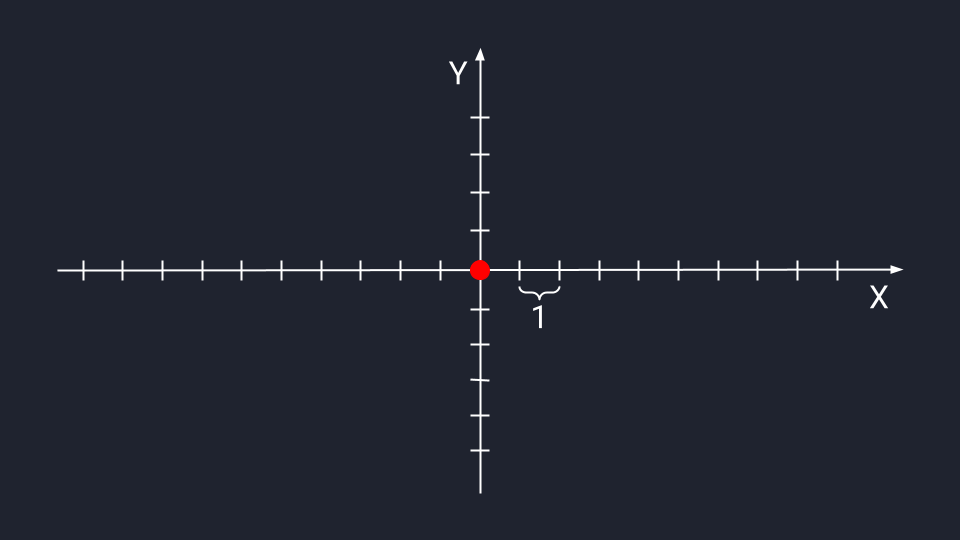
👉 Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами.

Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Как записывать

Вектор можно записать в строку или в столбец. Для строчной записи вектор обозначают одной буквой, ставят над ней черту, открывают круглые скобки и через запятую записывают координаты вектора. Для записи в столбец координаты вектора нужно взять в круглые или квадратные скобки — допустим любой вариант.

Строгий порядок записи делает так, что каждый набор чисел создаёт только один вектор, а каждый вектор ассоциируется только с одним набором чисел. Это значит, что если у нас есть координаты вектора, то мы их не сможем перепутать.

Способы записи вектора

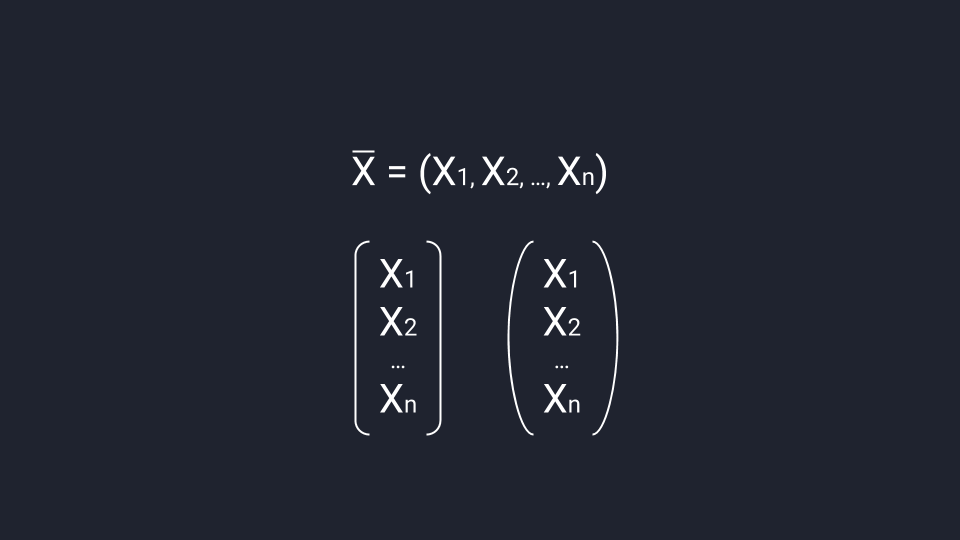
Скаляр

Помимо понятия вектора есть понятие скаляра. Скаляр — это просто одно число. Можно сказать, что скаляр — это вектор, который состоит из одной координаты.

Помните физику? Есть скалярные величины и есть векторные. Скалярные как бы описывают просто состояние, например, температуру. Векторные величины ещё и описывают направление.

Видео:Собственные векторы и собственные значения матрицыСкачать

Как изображать

Вектор из одного числа (скаляр) отображается в виде точки на числовой прямой.

Графическое представление скаляра. Записывается в круглых скобках

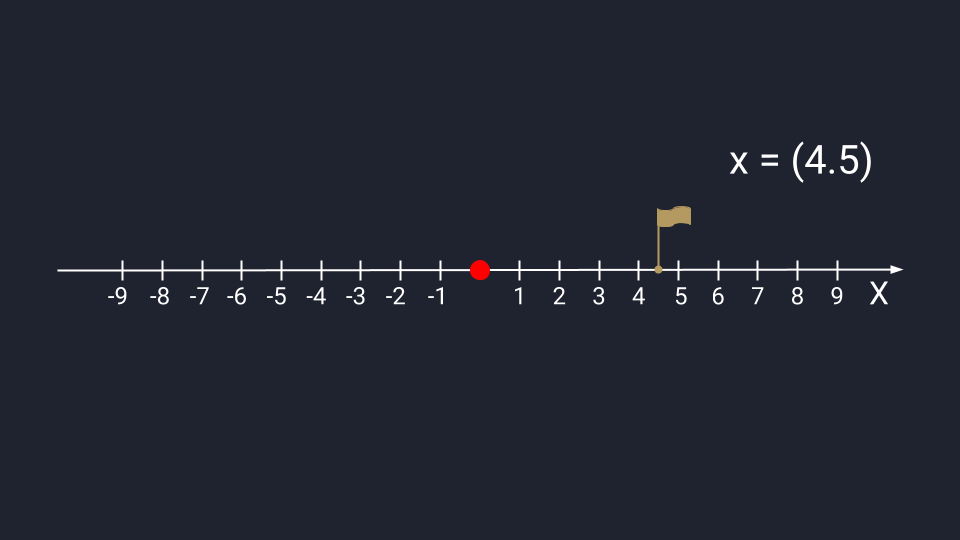
Вектор из двух чисел отображается в виде точки на плоскости осей Х и Y. Числа задают координаты вектора в пространстве — это такая инструкция, по которой нужно перемещаться от хвоста к стрелке вектора. Первое число показывает расстояние, которое нужно пройти вдоль оси Х; второе — расстояние по оси Y. Положительные числа на оси Х обозначают движение вправо; отрицательные — влево. Положительные числа на оси Y — идём вверх; отрицательные — вниз.

Представим вектор с числами −5 и 4. Для поиска нужной точки нам необходимо пройти влево пять шагов по оси Х, а затем подняться на четыре этажа по оси Y.

Графическое представление числового вектора в двух измерениях

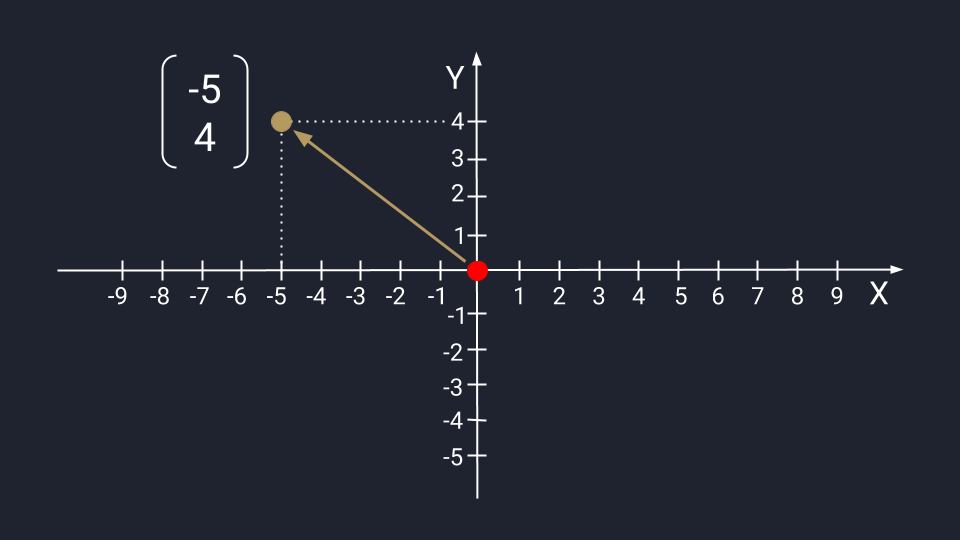
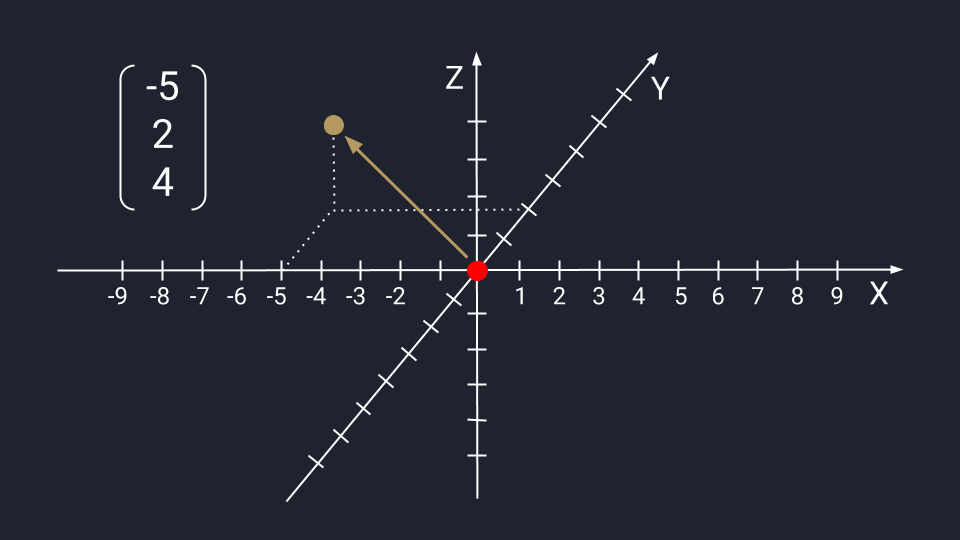
Вектор из трёх чисел отображается в виде точки на плоскости осей Х, Y и Z. Ось Z проводится перпендикулярно осям Х и У — это трёхмерное измерение, где вектор с упорядоченным триплетом чисел: первые два числа указывают на движение по осям Х и У, третье — куда нужно двигаться вдоль оси Z. Каждый триплет создаёт уникальный вектор в пространстве, а у каждого вектора есть только один триплет.

Если вектор состоит из четырёх и более чисел, то в теории он строится по похожему принципу: вы берёте координаты, строите N-мерное пространство и находите нужную точку. Это сложно представить и для обучения не понадобится.

Графическое представление числового вектора в трёх измерениях. Для примера мы взяли координаты −5, 2, 4

Помните, что все эти записи и изображения с точки зрения алгебры не имеют отношения к нашему реальному трёхмерному пространству. Вектор — это просто какое-то количество абстрактных чисел, собранных в строгом порядке. Вектору неважно, сколько там чисел и как их изображают люди. Мы же их изображаем просто для наглядности и удобства.

Например, в векторе спокойно может быть 99 координат. Для его изображения нам понадобилось бы 99 измерений, что очень проблематично на бумаге. Но с точки зрения вектора это не проблема: перемножать и складывать векторы из двух координат можно так же, как и векторы из 9999999 координат, принципы те же.

Видео:Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

И зачем нам это всё

Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например:

На основании векторов получаются матрицы. Если вектор — это как бы линия, то матрица — это как бы плоскость или таблица.
Машинное обучение в своей основе — это перемножение матриц. У тебя есть матрица с данными, которые машина знает сейчас; и тебе нужно эту матрицу «дообучить». Ты умножаешь существующую матрицу на какую-то другую матрицу и получаешь новую матрицу. Делаешь так много раз по определённым законам, и у тебя обученная модель, которую на бытовом языке называют искусственным интеллектом.

Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте.

И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.

Видео:Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать

Что дальше

В следующий раз разберём операции с векторами. Пока мы готовим материал — рекомендуем почитать интервью с Анастасией Никулиной. Анастасия ведёт ютуб-канал по дата-сайнс и работает сеньором дата-сайентистом в Росбанке.