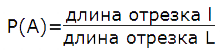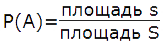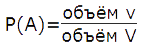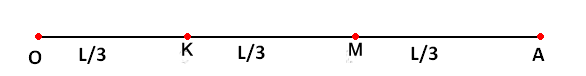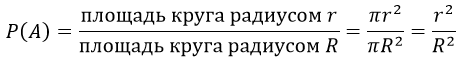Вероятность попадания в треугольник (5 видео)

Геометрическая вероятность

Цели и задачи: 1) Познакомить учащихся с одним из возможных способов задания

2) Повторение пройденного и закрепление навыков формализации

текстовых вероятностных задач с помощью геометрических фигур.

1) Знать определение геометрической вероятности выбора точки

внутри фигуры на плоскости и прямой;

2) Уметь решать простейшие задачи на геометрическую вероятность,

зная площади фигур или умея их вычислять.

I. Выбор точки из фигуры на плоскости.

Пример 1. Рассмотрим мысленный эксперимент: точку наудачу бросают на квадрат, сторона которого равна 1. Спрашивается, какова вероятность события, которое состоит в том, что расстояние от этой точки до ближайшей стороны квадрата не больше чем ?

В этой задаче речь идет о так называемой геометрической вероятности.

Рассмотрим более общие условия опыта.

Точку наудачу бросают в фигуру F на плоскости. Какова вероятность того, что точка попадает в некоторую фигуру G, которая содержится в фигуре F.

Ответ зависит от того, какой смысл мы вкладываем в выражение «бросить точку наудачу».

Обычно это выражение трактуют так:

1. Брошенная точка может попасть в любую часть фигуры F.

2. Вероятность того, что точка попадает в некоторую фигуру G внутри фигуры F, прямо пропорциональна площади фигуры G.

Подведем итог: пусть и — площади фигур F и G . Вероятность события А «точка Х принадлежит фигуре G, которая содержится в фигуре F», равна

Заметим, что площадь фигуры G не больше, чем площадь фигуры F, поэтому

Вернемся к нашей задаче. Фигура F в этом примере квадрат со стороной 1. Поэтому =1.

Точка удалена от границы квадрата не более чем на , если она попала в заштрихованную на рисунке фигуру G. Чтобы найти площадь , нужно из площади фигуры F вычесть площадь внутреннего квадрата со стороной .

Тогда вероятность того, что точка попала в фигуру G, равна

Пример 2. Из треугольника АВС случайным образом выбирается точка Х. Найти вероятность того, что она принадлежит треугольнику, вершинами которого являются середины сторон треугольника.

Решение: Средние линии треугольника разбивают его на 4 равных треугольников. Значит,

Вероятность того, что точка Х принадлежит треугольнику KMN, равна:

Вывод. Вероятность попадания точки в некоторую фигуру прямо пропорциональна площади этой фигуры.

Задача. Нетерпеливые дуэлянты.

Дуэли в городе Осторожности редко кончаются печальным исходом. Дело в том, что каждый дуэлянт прибывает на место встречи в случайный момент времени между 5 и 6 часами утра и, прождав соперника 5 минут, удаляется. В случае же прибытия последнего в эти 5 минут дуэль состоится. Какая часть дуэлей действительно заканчивается поединком?

Решение: Пусть х и у обозначают время прибытия 1-го т 2-го дуэлянтов соответственно, измеренное в долях часа начиная с 5 часов.

Дуэлянты встречаются, если , т. е. x —

Видео:Геометрическая вероятностьСкачать

Геометрическое определение вероятности

Геометрическое определение вероятности применимо для несовместных событий, в которых число равновозможных исходов бесконечно, например, попадания точки на участок отрезка, плоскости, пространства, объёма.

Общая формула для определения геометрической вероятности:

Отношение меры области g, благоприятствующей событию А, к мере всей области G.

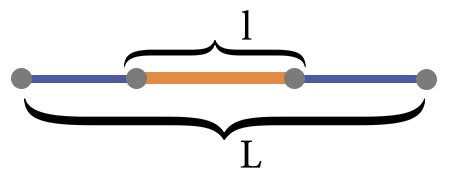
Формула геометрической вероятности попадания точки на участок отрезка L для одномерного пространства равна:

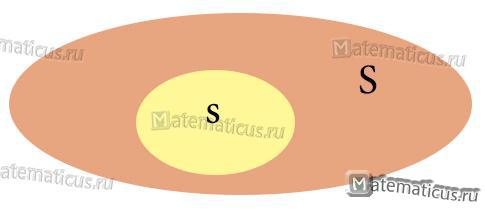
Формула геометрической вероятности попадания точки в область пространства S для фигур в двухмерном пространстве равна:

Формула геометрической вероятности попадания точки в заданный объём для фигур в трёхмерном пространстве V равна:

Пример 1

Решение

Пример 2

Решение

Аналогично первому примеру, вероятность равна:

P(A)=l/L=10/20=1/2

Пример 3

В круг радиуса R помещен меньший круг радиуса r. Найти вероятность того, что точка, наудачу брошенная в большой круг, попадет также и в малый круг. Предполагается, что вероятность попадания точки в круг пропорциональна площади круга и не зависит от его расположения.

Пример 4

Быстро вращающийся диск разделен на четное число равных секторов, попеременно окрашенных в белый и черный цвет. По диску произведен выстрел. Найти вероятность того, что пуля попадет в один из белых секторов. Предполагается, что вероятность попадания пули в плоскую фигуру пропорциональна площади этой фигуры

Решение

P(A)=0.5·πr 2 /πr 2 =0.5

Пример 5

Два студента условились встретиться в определенном месте между 12 и 13 часами дня. Пришедший первым ждет второго в течение 1/4 часа, после чего уходит. Найти вероятность того, что встреча состоится, если каждый студент наудачу выбирает момент своего прихода (в промежутке от 12 до 13 часов).

Видео:Теория вероятностей | Математика TutorOnlineСкачать

Алгебра и начала математического анализа. 11 класс

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №37. Геометрическая вероятность.

Перечень вопросов, рассматриваемых в теме:

Геометрическая вероятность
Задачи на геометрическую вероятность

Глоссарий по теме

Испытанием называется осуществление определенных действий.

Под событием понимают любой факт, который может произойти в результате испытания.

Любой результат испытания называется исходом.

Достоверным называют событие, которое в результате испытания обязательно произойдёт.

Невозможным называют событие, которое заведомо не произойдёт в результате испытания.

Геометрической вероятностью некоторого события называется отношение P(A) = g/G, где G – геометрическая мера, выражающая общее число всех равновозможных исходов данного испытания, а g – мера, выражающая количество благоприятствующих событию A исходов

Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. Под ред. А.Б. Жижченко. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни. – 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-022250

Виленкин Н. Я., Ивашев-Мусатов О. С., Шварцбурд С. И. Алгебра и математический анализ для 11 класса: Учеб. пособие для учащихся шк. и классов с углубл. изуч. математики. — 4-е изд. — М.: Просвещение, 1995. — 288 с.: ил. — ISBN 5-09-0066565-9. сс.253-259.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.

Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.

Теоретический материал для самостоятельного изучения

Вероятность наступления некоторого события A в испытании равна P(A) = g/G, где G – геометрическая мера, выражающая общее число всех равновозможных исходов данного испытания, а g – мера, выражающая количество благоприятствующих событию A исходов.

Пусть на плоскости задана некоторая область D, площадь которой равна S(D), и в ней содержится область d, площадь которой равна s(d). В области D наудачу ставится точка. Тогда вероятность события А – «точка попадает в область d» равна числу P(A) = s(d)/S(D).

Рисунок 1 — иллюстрация геометрической вероятностей

Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Вероятность попадания точки на отрезок l равна P(A) = |l|/|L|.

Пусть пространственная фигура d составляет часть фигуры D. В фигуру D наудачу ставится точка. Вероятность попадания точки в фигуру d равна P(A) = V(d)/V(D).

Пример использования геометрического определения вероятности при решении задачи.

Два друга договорились встретиться в определенном месте между 12 и 13 часами. Пришедший первым ждет другого в течении 20 минут, после чего уходит. Чему равна вероятность встречи друзей, если приход каждого из них может произойти

наудачу в течении указанного часа и моменты прихода независимы?

х — момент прихода первого друга

y — момент прихода второго друга

Рисунок 2 — Иллюстрация к задаче

S=60 2 –2·1/2·40 2 =2000

P(A) = 2000/60 2 = 5/9.

Ответ: вероятность встречи 5/9.

Примеры и разбор решения заданий тренировочного модуля

Пример 1. Метровый шнур случайным образом разрезают ножницами. Найти вероятность того, что длина обрезка составит не менее 80 см.

Общему числу исходов соответствует длина шнура 1 м. Чтобы длина обрезка составила не менее 0,8 м, можно отрезать не более 0,2 м. Такие отрезы можно выполнить с любой стороны шнура, их суммарная длина равна 0,2+0,2=0,4 м. По геометрическому определению:

Пример 2. В шар брошена случайная точка.

2а) С какой вероятностью она попадёт в центр шара?

Объём одной точки (центра шара) равен нулю, значит и искомая вероятность равна 0

2б) С какой вероятностью она попадёт на какой-нибудь диаметр шара?

Любая точка шара всегда попадает на какой-нибудь диаметр. Поэтому вероятность равна единице.

2в) С какой вероятностью она попадёт в одно, определённое, полушарие?

При решении этой задачи используем отношение объемов фигур. Пусть весь объём шара равен V. Все точки шара — трёхмерная фигура Ω. Искомая вероятность равна отношению объёма полушария V(A) к объёму шара V:

Пример 3. В круг радиуса см вписан равнобедренный прямоугольный треугольник. В круг наудачу ставится точка. Найдите вероятность того, что она не попадёт в данный треугольник. При необходимости в расчетах используйте значение π с точностью до целых.

Площадь круга равна

Гипотенуза прямоугольного треугольника, вписанного в круг, равна диаметру круга (прямой угол опирается на диаметр), то есть .

Поскольку треугольник равнобедренный, его катеты равны между собой, и по теореме Пифагора каждый катет равен . Площадь такого треугольника будет равна (можно найти площадь треугольника, не вычисляя длины катета: рассмотрим квадрат со стороной, равной гипотенузе нашего треугольника, площадь такого квадрата в четыре раза больше площади треугольника