Задачи огэ на площади четырехугольников

Практический материал для отработки задания №18 ОГЭ 2020 по математике — тренинг по теме: «Площадь четырёхугольника».

Разработка содержит 9 задач с ответами по материалам работ системы Статград.

Данные задачи относятся к 7 разделу кодификатора Геометрия.

7.3.1 Параллелограмм, его свойства и признаки

7.3.2 Прямоугольник, квадрат, ромб, их свойства и признаки

7.3.3 Трапеция, средняя линия трапеции; равнобедренная трапеция

Видео:Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Подборка задач ОГЭ по теме «Площадь» для 8 класса

В разработке подобраны задачи на нахождение площади треугольников, четырёхугольников из ОГЭ

Просмотр содержимого документа
«Подборка задач ОГЭ по теме «Площадь» для 8 класса»

1. Сторона квадрата равна 10. Найдите его площадь.

2. Периметр квадрата равен 40. Найдите площадь квадрата.

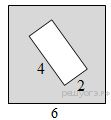
3.Из квадрата вырезали прямоугольник. Найдите площадь получившейся фигуры.

4. Периметр квадрата равен 160. Найдите площадь квадрата.

5. Найдите площадь квадрата, если его диагональ равна 1.

6. Найдите площадь квадрата, описанного вокруг окружности радиуса 83.

1. В пря­мо­уголь­ни­ке одна сто­ро­на равна 10, дру­гая сторона равна 12. Най­ди­те площадь прямоугольника.

2. В пря­мо­уголь­ни­ке диагональ равна 10, а угол между ней и одной из сто­рон равен 30°. Най­ди­те площадь прямоугольника, делённую на .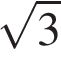

3. В пря­мо­уголь­ни­ке диагональ равна 10, угол между ней и одной из сто­рон равен 30°, длина этой сто­ро­ны . Най­ди­те площадь прямоугольника, деленную на

4. Найдите пло­щадь прямоугольника, если его пе­ри­метр равен 44 и одна сто­ро­на на 2 боль­ше другой.

5. Найдите пло­щадь прямоугольника, если его пе­ри­метр равен 60, а от­но­ше­ние со­сед­них сто­рон равно 4:11.

6. Найдите пло­щадь прямоугольника, если его пе­ри­метр равен 58 и одна сто­ро­на на 5 боль­ше другой.

7. В пря­мо­уголь­ни­ке одна сто­ро­на равна 96, а диа­го­наль равна 100. Най­ди­те пло­щадь пря­мо­уголь­ни­ка.

8. На сто­ро­не BC пря­мо­уголь­ни­ка ABCD, у ко­то­ро­го AB = 12 и AD = 17, от­ме­че­на точка E так, что ∠EAB = 45°. Най­ди­те ED.

В пря­мо­уголь­ном треугольнике один из ка­те­тов равен 10, а угол, ле­жа­щий напротив него, равен 45°. Най­ди­те площадь треугольника.

Най­ди­те пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка, если его катет и ги­по­те­ну­за равны со­от­вет­ствен­но 28 и 100.

В пря­мо­уголь­ном тре­уголь­ни­ке один из ка­те­тов равен 4, а ост­рый угол, при­ле­жа­щий к нему, равен 45°. Най­ди­те пло­щадь тре­уголь­ни­ка.

В пря­мо­уголь­ном тре­уголь­ни­ке ги­по­те­ну­за равна 70, а один из ост­рых углов равен 45°. Най­ди­те пло­щадь тре­уголь­ни­ка.

Катеты прямоугольного треугольника равны 8 и 15. Найдите гипотенузу этого треугольника.

Два катета прямоугольного треугольника равны 4 и 9. Найдите площадь этого треугольника.

Сторона рав­но­сто­рон­не­го треугольника равна 10. Най­ди­те его площадь, делённую на .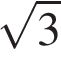

Периметр рав­но­сто­рон­не­го треугольника равен 30. Най­ди­те его площадь, делённую на .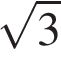

Высота рав­но­сто­рон­не­го треугольника равна 10. Най­ди­те его площадь, делённую на

В рав­но­бед­рен­ном треугольнике бо­ко­вая сторона равна 10, а угол, ле­жа­щий напротив основания, равен 120°. Най­ди­те площадь треугольника, делённую на

Периметр рав­но­бед­рен­но­го треугольника равен 16, а бо­ко­вая сторона — 5. Най­ди­те площадь треугольника.

В рав­но­бед­рен­ном треугольнике бо­ко­вая сторона равна 10, основание — 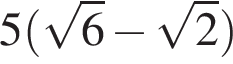, а угол, ле­жа­щий напротив основания, равен 30°. Най­ди­те площадь треугольника.

Бо­ко­вая сто­ро­на рав­но­бед­рен­но­го тре­уголь­ни­ка равна 34, а ос­но­ва­ние равно 60. Най­ди­те пло­щадь этого тре­уголь­ни­ка.

Пе­ри­метр рав­но­бед­рен­но­го тре­уголь­ни­ка равен 216, а бо­ко­вая сто­ро­на — 78. Най­ди­те пло­щадь тре­уголь­ни­ка.

В тре­уголь­ни­ке одна из сто­рон равна 10, а опу­щен­ная на нее высота — 5. Най­ди­те площадь треугольника.

В тре­уголь­ни­ке одна из сто­рон равна 10, дру­гая равна , а угол между ними равен 60°. Най­ди­те площадь треугольника.

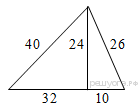
Най­ди­те пло­щадь тре­уголь­ни­ка, изоб­ражённого на ри­сун­ке.

В тре­уголь­ни­ке ABC от­ре­зок DE — сред­няя линия. Пло­щадь тре­уголь­ни­ка CDE равна 97. Най­ди­те пло­щадь тре­уголь­ни­ка ABC.

Сторона треугольника равна 12, а высота, проведённая к этой стороне, равна 33. Найдите площадь этого треугольника.

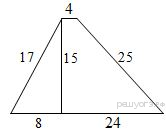
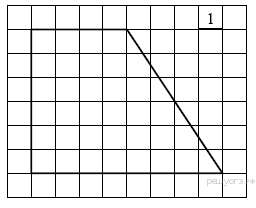
1. Най­ди­те площадь трапеции, изображённой на рисунке.

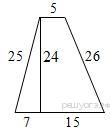
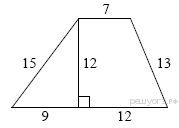
2. Основания тра­пе­ции равны 18 и 12, одна из бо­ко­вых сторон равна , а угол между ней и одним из ос­но­ва­ний равен 135°. Най­ди­те площадь трапеции.

3. Основания тра­пе­ции равны 18 и 12, одна из бо­ко­вых сторон равна 6, а синус угла между ней и одним из ос­но­ва­ний равен 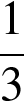. Най­ди­те площадь трапеции.

4. Основания тра­пе­ции равны 18 и 12, одна из бо­ко­вых сторон равна 6, а ко­си­нус угла между ней и одним из ос­но­ва­ний равен 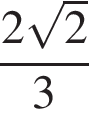. Най­ди­те площадь трапеции.

5. Основания тра­пе­ции равны 18 и 12, одна из бо­ко­вых сторон равна 6, а тан­генс угла между ней и одним из ос­но­ва­ний равен 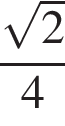. Най­ди­те площадь трапеции.

6. Средняя линия тра­пе­ции равна 11, а мень­ше основание равно 5. Най­ди­те большее ос­но­ва­ние трапеции.

7. Бо­ко­вая сто­ро­на тра­пе­ции равна 5, а один из при­ле­га­ю­щих к ней углов равен 30°. Най­ди­те пло­щадь тра­пе­ции, если её ос­но­ва­ния равны 3 и 9.

8. В рав­но­бед­рен­ной тра­пе­ции ос­но­ва­ния равны 3 и 9, а один из углов между бо­ко­вой сто­ро­ной и ос­но­ва­ни­ем равен 45°. Най­ди­те пло­щадь тра­пе­ции.

9. Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 5 и 17, а ее бо­ко­вые сто­ро­ны равны 10. Най­ди­те пло­щадь тра­пе­ции.

10. Ос­но­ва­ния тра­пе­ции равны 7 и 49, одна из бо­ко­вых сто­рон равна 18 , а ко­си­нус угла между ней и одним из ос­но­ва­ний равен 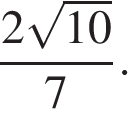Най­ди­те пло­щадь тра­пе­ции.

11.Основания тра­пе­ции равны 1 и 13, одна из бо­ко­вых сто­рон равна , а угол между ней и одним из ос­но­ва­ний равен 135°. Най­ди­те пло­щадь трапеции.

12. В тра­пе­ции ABCD AD = 5, BC = 2, а её пло­щадь равна 28. Най­ди­те пло­щадь тра­пе­ции BCNM, где MN – сред­няя линия тра­пе­ции ABCD.

13. В тра­пе­ции ABCD AD = 3, BC = 1, а её пло­щадь равна 12. Най­ди­те пло­щадь тре­уголь­ни­ка ABC.

14. Тангенс остро­го угла пря­мо­уголь­ной тра­пе­ции равен 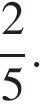Най­ди­те её боль­шее основание, если мень­шее ос­но­ва­ние равно вы­со­те и равно 58.

15. Основания трапеции равны 9 и 54, одна из боковых сторон равна 27, а косинус угла между ней и одним из оснований равен 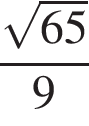. Найдите площадь трапеции.

16.В тра­пе­ции ABCD известно, что AD = 6, BC = 2, а её пло­щадь равна 32. Най­ди­те пло­щадь тра­пе­ции BCNM, где MN – сред­няя линия тра­пе­ции ABCD.

17. В тра­пе­ции ABCD известно, что AD = 5, BC = 1, а её пло­щадь равна 51. Най­ди­те пло­щадь тра­пе­ции BCNM, где MN – сред­няя линия тра­пе­ции ABCD.

18. Основания тра­пе­ции равны 6 и 24, одна из бо­ко­вых сторон равна 11, а синус угла между ней и одним из ос­но­ва­ний равен . Най­ди­те площадь трапеции.

19. Основания тра­пе­ции равны 7 и 63, одна из бо­ко­вых сторон равна 18, а ко­си­нус угла между ней и одним из ос­но­ва­ний равен . Най­ди­те площадь трапеции.

1. Найдите пло­щадь параллелограмма, изображённого на рисунке.

2. Сторона ромба равна 5, а диа­го­наль равна 6. Най­ди­те площадь ромба.

3. Периметр ромба равен 40, а один из углов равен 30°. Най­ди­те пло­щадь ромба.

4. Периметр ромба равен 24, а синус од­но­го из углов равен 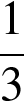. Най­ди­те площадь ромба.

5. Одна из сто­рон параллелограмма равна 12, а опу­щен­ная на нее вы­со­та равна 10. Най­ди­те площадь параллелограмма.

6. Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а один из углов — 45°. Най­ди­те площадь параллелограмма, делённую на .

7. Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а синус од­но­го из углов равен 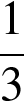. Най­ди­те площадь параллелограмма.

8. Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а ко­си­нус одного из углов равен 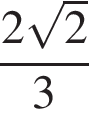. Най­ди­те площадь параллелограмма.

9. Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а тан­генс одного из углов равен 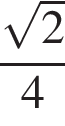. Най­ди­те площадь параллелограмма.

10. Най­ди­те пло­щадь ромба, если его диа­го­на­ли равны 14 и 6.

11. В ромбе сто­ро­на равна 10, одна из диагоналей — 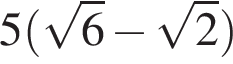, а угол, ле­жа­щий напротив этой диагонали, равен 30°. Най­ди­те площадь ромба.

12. Пло­щадь па­рал­ле­ло­грам­ма ABCD равна 56. Точка E — се­ре­ди­на сто­ро­ны CD. Най­ди­те пло­щадь тра­пе­ции AECB.

13. Сто­ро­на ромба равна 9, а рас­сто­я­ние от цен­тра ромба до неё равно 1. Най­ди­те пло­щадь ромба.

14. Пе­ри­метр ромба равен 116, а один из углов равен 30°. Най­ди­те пло­щадь ромба.

15. Сто­ро­на ромба равна 50, а диа­го­наль равна 80. Най­ди­те пло­щадь ромба.

17. Высота BH па­рал­ле­ло­грам­ма ABCD делит его сто­ро­ну AD на от­рез­ки AH = 1 и HD = 28. Диа­го­наль параллелограмма BD равна 53. Най­ди­те площадь параллелограмма.

Фигуры на квадратной решётке

На клетчатой бумаге с размером клетки 1см × 1см найти площадь фигуры

Видео:Лайфхак! Площади всех фигур #огэ #математика #shortsСкачать

Занятие на тему «Площади четырехугольников» (Подготовка к ОГЭ».

Видео:ОГЭ 2022 по математике. Задания 17,18. Площадь четырехугольников, кругаСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Выбранный для просмотра документ Задачи.docx

Задачи по теме «Площадь».

Площадь прямоугольного земельного участка равна 13 га, ширина участка равна 260 м. Найдите длину этого участка в метрах.

П ол комнаты, имеющей форму прямоугольника со сторонами 4 м и 9 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 25 см. Сколько потребуется таких дощечек?

Выбранный для просмотра документ Площадь четырехугольников.docx

Обобщить и систематизировать теоретические знания учащихся по теме “Площадь четырехугольников”.

Совершенствовать навыки решения задач, развивать логическое мышление, память, познавательный интерес, продолжать формирование математической речи и графической культуры, способствовать развитию творческой деятельности, воображения.

Прививать трудолюбие, настойчивость, доброжелательность, воспитывать честность в оценке своих знаний и знаний одноклассников.

Ход занятия (краткое описание).

Объявление темы, целей занятия.

Актуализация знаний учащихся.

Повторение и систематизация теоретического материала по теме «Площадь четырехугольников» по плану:

формулы для вычисления площади

с использованием презентации ( Слайды 2 – 7) , при необходимости опорной таблицы для каждого ученика ( Приложение 1 )

Самостоятельное решение задач из Открытого банка заданий ОГЭ (1 часть) по готовым чертежам с последующей самопроверкой (Слайды 8 – 16).

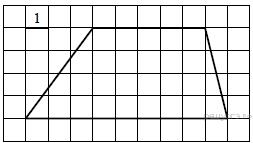
№ 1. Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.

№ 2. Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.

№ 3. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH =8 и HD =40. Диагональ параллелограмма BD равна 50. Найдите площадь параллелограмма.

№ 4. Найдите площадь параллелограмма, изображённого на рисунке.

№ 5. Периметр ромба равен 116, а один из углов равен 30 ∘ . Найдите площадь ромба.

№ 6. Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба.

№ 7. Найдите площадь трапеции, изображённой на рисунке.

№ 8. В равнобедренной трапеции основания равны 3 и 5, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.

№ 9. Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 7.

2)

Коллективное решение задач из II части (Слайды 17 – 19) .

№ 1. Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K . Найдите площадь параллелограмма, если BC =2, а расстояние от точки K до стороны AB равно 1.

№ 2. Внутри параллелограмма ABCD выбрали произвольную точку E . Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.

№ 3. В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60° , сторона AB равна 4. Найдите площадь трапеции.

Мне было полезно …

Я сегодня разобрался …

Я сегодня понял, что …

Мне было трудно …

На следующем занятии я хочу …

Выбранный для просмотра документ Площадь четырехугольников.pptx

Описание презентации по отдельным слайдам:

ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА Параллелограмм В С F АЕ Д S= AD * BE = CD * BF S= AB * AD* sinA= = BA* BC* sinB

ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА Прямоугольник В С А Д S= AB*BC

ПЛОЩАДЬ КВАДРАТА Квадрат BC d AaD AC = d S = a2 S =½d2

ПЛОЩАДЬ РОМБА Ромб В Н А С Д S=AC* BD S=AB2sinA= AB2sinB S= AB*СH

ПЛОЩАДЬ ТРАПЕЦИИ Трапеция C B AD H S=(BC+ AD)*BH

ПЛОЩАДЬ ВЫПУКЛОГЛО ЧЕТЫРЕХУГОЛЬНИКА Выпуклый четырёхугольник C B AD S =AC*BD*sin

Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке. А В С D Е F G M Выполним дополнительные построения. SABCD = SABEF – SCED – SADF SABEF = 36 кв.ед. SCED = ½ (1*5) = 2,5 кв.ед. SADF = ½ (1*6) = 3 кв.ед. SABCD = 36 – 2,5 – 3 = 30,5 (кв.ед.)

Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры. S = 62 — 4*2 = 28(кв.ед.)

Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=8 и HD=40. Диагональ параллелограмма BD равна 50. Найдите площадь параллелограмма. SABCD = AD * BH AD = 8 + 40 =48 BH2 = BD2 – HD2 BH2 = 2500 – 1600 = 900 BH = 30 SABCD = 48 * 30 = 1440 (кв.ед.)

Найдите площадь параллелограмма, изображённого на рисунке. S = a*h S = (3 + 7) *4 = 40 (кв.ед.)

Периметр ромба равен 116, а один из углов равен 30∘. Найдите площадь ромба. S = AB2 * Sin B AB = 116: 4 = 29 S = 292 * ½ = 420,5 (кв.ед.) A B C D 30°

Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба. S = a*h h = S/a a = P/4 a = 9 h = 27/9 = 3 A B C D a h

Найдите площадь трапеции, изображённой на рисунке. S = ½ (a + b) *h a b h S = ½ ( 5+9) *4 = 28 (кв.ед.)

В равнобедренной трапеции основания равны 3 и 5, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции. S = ½ (a + b)*h h = (5 – 3):2 = 1 S = ½ (3 + 5)*1 = 4

Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 7. S = ½ (a + b)*h h = ½*4 = 2 S = ½ (2 + 7)*2 = 9

1. Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=2, а расстояние от точки K до стороны AB равно 1. Задачи II части Обозначим точки пересечения биссектрис со сторонами точками E и F соответственно. FAK =  BEK (т.к. накрест лежащие). FAK=BEK,  ΔABE – равнобедренный,  AB = BE. Δ ABK = Δ EBK по стороне и двум прилежащим углам,  высоты у этих треугольников тоже равны. Аналогично, ΔABK = ΔAFK,  высота параллелограмма равна 2h. SABCD = BC*2h; SABCD = 2*2*1= 4

2. Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма. Проведем отрезок MN, перпендикулярный сторонам AD и BC, проходящий через точку Е. S ABCD = AD*MN; SAED = ½ AD*EM; SBEC = ½ BC*EN; AD = BC; SAED + SBEC = ½ AD*EM +½ BC*EN= ½ *AD (EM+EN) = ½*AD*MN = ½* S ABCD . M N E

В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°,сторона AB равна 4. Найдите площадь трапеции. Проведем высоты BE и CF. SABCD = ½ ( BC + AD)*CF Обозначим: ВС = СD = EF = x, AD = 2x по условию. ΔCDF — прямоугольный, т.к. CF-высота. FCD=180°-90°-60°=30°. FD = ½ CD по св-ву прямоугольного треугольника,  FD = 1/2x, AE = 2x – x – 1/2x = 1/2x ,  AE = FD. ΔABE =ΔDCF (по двум катетам),  A = D – трапеция равнобедренная. CD = 4; FD =2; AD = 8 CF = CD2 – FD2 (по теореме Пифагора); CF =  16 – 4 = 12 SABCD = ½ (8 + 16)* 12 = 24 3 Е F

Режим тренировки Задание 11 Тестирование по теме «Площадь» https://ege.yandex.ru/mathematics-gia/#training

ПРОДОЛЖИ ФРАЗУ: Мне было полезно … Я сегодня разобрался … Я сегодня понял, что … Мне было трудно … На следующем занятии я хочу …

ЗАДАНИЕ НА ДОМ: Карточки с задачами 1 части.

Выбранный для просмотра документ Таблицы Площади четырехугольников.docx

Параллелограмм

🌟 Видео

Задача по геометрии № 25 ОГЭ на отношение площадейСкачать

ОГЭ по математике. Площадь четырехугольника можно вычислить по формуле (вар. 5)Скачать

Площади четырехугольников. Открытый банк ОГЭ #20🔴Скачать

ПЛОЩАДЬ ЧЕТЫРЕХУГОЛЬНИКА 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Геометрия 8. Урок 13 - Площадь четырехугольников. ЗадачиСкачать

ОГЭ по математике. Площадь четырехугольника можно вычислить (вар. 4)Скачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

9 класс. Математика. Подготовка к ОГЭ. Площадь четырехугольниковСкачать

Четырёхугольники №17 из ОГЭ. Площади. Площади частей фигур.Скачать

ВСЯ ГЕОМЕТРИЯ ИЗ ОГЭ ПО МАТЕМАТИКЕ 2023 ЗА 40 МИНУТСкачать

Задача о площади четырехугольникаСкачать

Геометрия 8. Урок 12 - Площадь четырехугольников. Формулы.Скачать

Площади всех фигур на ОГЭ #огэ #огэматематика #умскулСкачать

Самый простой способ нахождения площадиСкачать

ОГЭ 24 задание Найти площадь четырехугольникаСкачать

ГЕОМЕТРИЯ ОГЭ задание 18 найти площадь четырехугольника с заданными координатами вершинСкачать