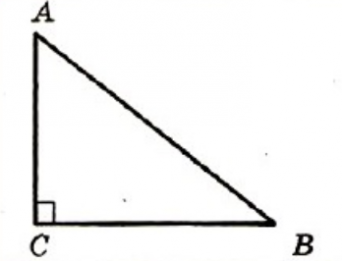
Когда прямоугольный треугольник не существует (3 видео)

Прямоугольный треугольник

Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).

Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.

Стороны, прилежащие к прямому углу, называются катетами .

Содержание

Прямоугольный треугольник. Теорема Пифагора.
теория по математике 📈 планиметрия
Свойства прямоугольного треугольника
Признаки равенства прямоугольных треугольников
Теорема Пифагора
Египетский треугольник
Пифагоровы тройки
Определить возможность существования треугольника по сторонам
Задача
Решение
💥 Видео

Признаки равенства прямоугольных треугольников

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).

Свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна 90˚.

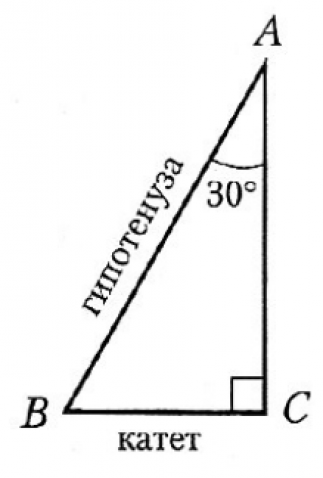
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.

И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

3. Теорема Пифагора:

, где – катеты, – гипотенуза. Видеодоказательство

4. Площадь прямоугольного треугольника с катетами :

5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:

6. Центр описанной окружности – есть середина гипотенузы.

7. Радиус описанной окружности есть половина гипотенузы :

8. Медиана, проведенная к гипотенузе, равна ее половине

9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:

Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.

Видео:Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

Прямоугольный треугольник. Теорема Пифагора.

теория по математике 📈 планиметрия

Если в треугольнике есть угол, равный 90 градусов, то такой треугольник называется прямоугольным. Стороны прямоугольного треугольника называются – катеты и гипотенуза. Катеты – это стороны, образующие прямой угол. Гипотенуза – сторона, которая располагается напротив прямого угла.

На рисунке треугольник АВС – прямоугольный, угол С равен 90º, стороны АС и ВС – катеты, а сторона АВ – гипотенуза.

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Свойства прямоугольного треугольника

В прямоугольном треугольнике гипотенуза является наибольшей стороной.
В прямоугольном треугольнике катет, лежащий напротив угла 30 0 , равен половине гипотенузы. И обратно, если катет равен половине гипотенузы, то угол, лежащий напротив этого катета, равен 30 0 .

Например, пусть угол А=30 0 , а гипотенуза АВ=28 см, то катет ВС будет равен 14 см, так как лежит напротив угла А=30 0 . Или, например, если катет ВС=6 см, а гипотенуза АВ равна 12 см, то угол А (лежащий напротив катета ВС), равен 30 0 .

Сумма острых углов прямоугольного треугольника равна всегда 90 градусов.
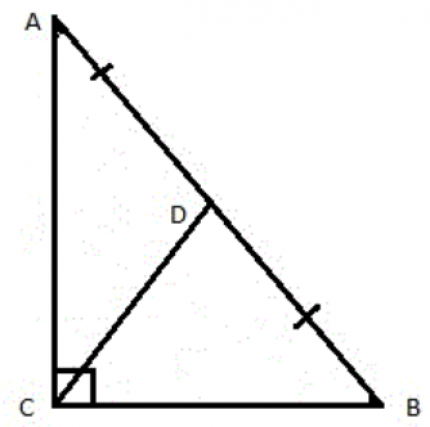
Медиана, проведенная к гипотенузе, равна её половине.

На рисунке изображен прямоугольный треугольник АВС, где CD – медиана, проведенная к гипотенузе. По свойству – медиана CD=0,5АВ, то есть AD=DB=CD.

Видео:Что с углами. Прямоугольный треугольник #shortsСкачать

Признаки равенства прямоугольных треугольников

Существует 4 признака равенства прямоугольных треугольников:

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Чтобы быстрее запомнить данные признаки, можно использовать их краткую трактовку:

по катетам;
по катету и прилежащему острому углу;
по гипотенузе и острому углу;
по гипотенузе и катету.

Видео:Нахождение стороны прямоугольного треугольникаСкачать

Теорема Пифагора

Древнегреческий философ, ученый, математик – Пифагор Самосский вывел теорему, которая до сих применима для решения задач. Теорема названа в честь него – «теорема Пифагора».

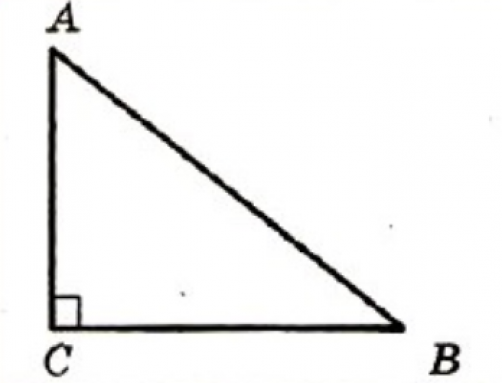
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

На рисунке в прямоугольном треугольнике АВ 2 =АС 2 +ВС 2

Например, если в данном треугольнике катеты равны 9 и 12 см, то можно найти длину гипотенузы, используя теорему: АВ 2 =9 2 +12 2 =81+144=225=15 2 , значит АВ=15 см.

Египетский треугольник

Треугольник со сторонами 3, 4 и 5 см называют Египетским треугольником.

Пифагоровы тройки

Тройки чисел, которые удовлетворяют теореме Пифагора, называют Пифагоровы тройки, а сами числа – Пифагоровы числа. Например, такими являются числа 16, 12 и 20 – это числа, которые при подстановке в формулу теоремы, дают нам верное равенство: 16 2 +12 2 =20 2 , 256+144=400, 400=400.

Видео:Свойства прямоугольного треугольника. 7 класс.Скачать

Определить возможность существования треугольника по сторонам

Задача

Треугольник существует только тогда, когда сумма любых двух его сторон больше третьей.

Дано: a , b , c – стороны предполагаемого треугольника.

Требуется сравнить длину каждого отрезка-стороны с суммой двух других. Если хотя бы в одном случае отрезок окажется больше суммы двух других, то треугольника с такими сторонами не существует.

Решение

Ниже приведены решения задачи на языке программирования Паскаль двумя способами. В первом случае все стороны проверяются в одном операторе if; во втором случае каждое условие проверяется отдельно, а программа содержит вложенные операторы if-else.

Программа 1 (предпочтительный способ решения):

В языке Паскаль логический оператор and имеет приоритет над операторам >, if проверяется, что каждая из сторон меньше суммы других. Если хотя бы одна будет больше, то все логическое выражение вернет ложь ( false ). В таком случае сработает ветка else .

В данном случае существование треугольника проверяется по-этапно. Если первое условие возвращает ложь, то программа переходит к последнему else. Если же первое условие соблюдено, то поток выполнения программы оказывается у вложенного if. Здесь проверяется уже второе условие. Если оно возвращает ложь, то программа переходит к предпоследнему else. Если и второе логическое выражение возвращает истину (true), то программа идет к третьему условию. При его соблюдении выполняется тело самого вложенного оператора if. При его несоблюдении сработает самое вложенное else.

Несмотря на то, что данная программа кажется длиннее, в определенных ситуациях она может выполняться быстрее, чем первая. Здесь если внешнее if возвращает ложь, то остальные логические выражения вообще не проверяются. В первой программе могут и проверяться (это зависит от особенностей языка программирования).