Выберите правильный ответ отрезок соединяющий две соседние вершины четырехугольника

Видео:Как правильно решить задание про четырёхугольник? / Разбор заданий на ОГЭ по геометрииСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Тест по теме «Понятие четырехугольника»

Цель: Проверить знание основных понятий и умения решать простейшие задачи по теме.

1) Отрезки, имеющие одну общую точку, которая является концом каждого из них, называются :

А) смежными, Б) соседними, В) пересекающимися.

2)В четырехугольнике АВСD точки А В, С, D называются:

А) точками , Б) углами, В) вершинами.

3) Вершины четырехугольника, непринадлежащие одной стороне, называются

А) противолежащими, Б) противоположными, В) параллельными

4) Периметром четырехугольника называется :

А) произведение длин двух соседних сторон четырехугольника,

Б) произведение длин всех сторон четырехугольника,

В) сумма длин всех сторон четырехугольника.

5)Диагональю четырехугольника называется :

А) прямая, соединяющая две противолежащие вершины четырехугольника,

Б) отрезок, соединяющий любые две вершины четырехугольника,

В) отрезок, соединяющий две противолежащие вершины четырехугольника.

6) В четырехугольнике АВСD А = 120 º , углы В, С, D равны между собой. Найдите углы В, С, D.

А) 20 º , Б) 80 º , В) 60 º.

7) Выберите верный ответ :

А) в четырехугольнике может быть три прямых угла и один острый,

Б) в четырехугольнике может быть четыре прямых угла,

В) в четырехугольнике может быть четыре острых угла.

8) Могут ли стороны четырехугольника 3дм, 4дм, 2дм, 9дм?

А) да, Б) нет, В) не знаю.

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 967 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 342 человека из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 689 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

• Глухова Светлана ВладимировнаНаписать 1996 20.09.2020

Номер материала: ДБ-1307176

07.09.2020 0

27.08.2020 0

26.08.2020 0

23.08.2020 0

19.08.2020 0

14.08.2020 0

05.08.2020 0

05.08.2020 0

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

В России разработают рекомендации по сопровождению студентов с ОВЗ

Время чтения: 2 минуты

Правительство направит регионам почти 92 миллиарда рублей на ремонт и оснащение школ

Время чтения: 1 минута

ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России

Время чтения: 1 минута

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:ЧЕТЫРЕХУГОЛЬНИК и его элементы. §1 геометрия 8 классСкачать

Выберите правильный ответ отрезок соединяющий две соседние вершины четырехугольника

Математику уж затем учить надо, что она ум в порядок приводит

1) Два отрезка называют соседними , если они имеют общую точку ,являющуюся концом каждого из них.

2) Фигуру , ограниченную частью плоскости , являющуюся такими , что никакие два соседних отрезка не лежат на одной прямой и никакие два не соседних отрезка не имеют общих точек , вместе с этими отрезками, называют четырёхугольником .

3) Стороны четырёхугольника , являющиеся соседними отрезками , называют соседними сторонами четырёхугольника .

4) Вершины четырёхугольника , являющиеся концами одной стороны называют соседними вершинами четырехугольника .

5) Стороны четырёхугольника, не являющиеся соседними, называют противолежащими (противоположными) сторонами четырёхугольника .

6) Несоседние вершины четырёхугольника называют противолежащими (противоположными) вершинами четырёхугольника .

7) Сумму длин сторон четырёх угольника называют периметром четырехугольника .

8) Отрезок , соединяющий противолежащие вершины четырехугольника, называют диагональю четырехугольника .

9) Четырёхугольник , все углы которого меньше развёрнутого угла называют выпуклым четырёхугольником .

10) Сумма углов четырёхугольника равна 360°.

11) В четырёхугольнике только один из углов может быть больше развернутого.

1) Два отрезка называют соседними , если они имеют ______________________ ,являющуюся ___________________________ каждого из них.

2) Фигуру , ограниченную частью плоскости , являющуюся такими , что никакие два ________________ отрезка не лежат __________________________ и никакие ___________________ отрезка не имеют _____________________ , вместе с этими отрезками, называют четырёхугольником .

3) Стороны четырёхугольника , являющиеся соседними отрезками , называют _____________________ сторонами четырёхугольника .

4) Вершины четырёхугольника , являющиеся ________________________________ называют соседними вершинами четырехугольника .

5) Стороны четырёхугольника, не являющиеся соседними, называют ____________________________ сторонами четырёхугольника .

6) Несоседние вершины четырёхугольника называют _______________________________ вершинами четырёхугольника .

7) Сумму _______________________ четырёх угольника называют периметром четырехугольника .

8) Отрезок , соединяющий противолежащие вершины четырехугольника называют____________________ четырехугольника .

9) Четырёхугольник , все углы которого меньше развёрнутого угла называют ___________________ четырёхугольником .

10) Сумма углов четырёхугольника равна _______

11) В четырёхугольнике _____________________________ может быть больше развернутого.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Выберите правильный ответ отрезок соединяющий две соседние вершины четырехугольника

Сборник тестовых вопросов по геометрии 8 класс

Правильный вариант ответа отмечен знаком +

1. Как называется фигура, составленная из n-отрезков, расположенных на разных прямых? Причем n – любое целое число.

2. Какой вариант содержит верные составляющие многоугольника?

+стороны и вершины;

-стороны и медианы;

-вершины и диагонали;

-нет верного ответа.

3. Что это за понятие – диагональ многоугольника?

-отрезок, соединяющий исключительно соседние вершины;

+это отрезок, который соединяет две вершины, находящиеся не в соседях;

-биссектриса, которая может соединить как соседние, так и не соседние вершины;

-это медиана многоугольника.

4. Имеются рисунки. Следует указать какой из них не содержит многоугольник.

5. Если сложить все стороны многоугольника, то можно найти:

6. Если через сторону многоугольника проходит прямая, и она находится по одну сторону от него, то этот многоугольник…

7. Дана формула: (n–2)*180 0 . Что по ней можно найти?

-сумму сторон выпуклого многоугольника;

+сумму углов выпуклого многоугольника;

-сумму углов невыпуклого треугольника;

-сумму сторон любой фигуры.

8. Чему равна сумма углов выпуклого четырехугольника?

9. Если в четырехугольнике стороны, расположенные друг напротив друга, попарно параллельны и равны, но углы не прямые, как он называется?

10. Даны диагонали параллелограмма. Что можно о них сказать?

+они точкой пересечения делятся поровну;

-ничего не скажешь.

11. Фигура, у которой четыре вершины и пару сторон параллельны, а другие стороны не параллельны, называется…

12. Если один из углов трапеции прямой, то…

+она является прямоугольной;

-она будет равнобедренной;

-все стороны трапеции равны;

-все остальные углы трапеции прямые.

13. Что это такое – равнобедренная трапеция?

— трапеция с прямыми углами;

+трапеция с одинаковыми боковыми сторонами;

-трапеция с равными основаниями;

-трапеция с равными сторонами.

14. Бывает ли так, что все углы трапеции прямые?

-если соблюдены определенные условия;

-без рисунка этого не скажешь.

15. Может ли случиться такое, что каждая сторона трапеции равна всем остальным?

-только в исключительных случаях;

-не всегда, но такое возможно.

16. Про основания трапеции известно следующее:

-одно из них всегда является половиной другого;

+одно больше, другое меньше;

-одно из них постоянно больше другого в три раза.

17. Если в параллелограмме все углы прямые, то…

-ничего не поделаешь.

18. А что же насчет диагоналей прямоугольника?

+они исключительно всегда равны;

-они абсолютно никогда не будут равны;

-диагонали прямоугольника просто существуют в природе;

-о диагоналях прямоугольника не принято говорить всерьез.

19. Все стороны равны, он является параллелограммом… О какой фигуре идет речь?

20. Все углы прямые, он, естественно, параллелограмм, стороны тоже равны…Что это за фигура?

21. Его диагонали взаимно перпендикулярны, а также делят его углы пополам. Это про диагонали…

22. Чего нельзя сказать про диагонали квадрата?

-они равны и делят углы пополам;

-точкой пересечения делятся пополам;

+они всегда имеют фиксированную длину.

23. Про площади равных многоугольников можно сказать следующее:

+они имеют равные площади;

-они имеют разные площади;

-они соотносятся как один к двум;

-они соотносятся как один к трем.

24. Если многоугольник состоит из некоторых многоугольников, то его площадь…

-равна площади одного из многоугольников;

+равна сумме площадей данных многоугольников;

-равна половине суммы площадей этих многоугольников;

-равна произведения площадей этих многоугольников.

25. Если в квадрате известна только его сторона – можно ли найти его площадь?

26. Площадь прямоугольника равна:

+перемноженным смежным сторонам;

-сумме смежных сторон;

-произведению высоты на основание;

-произведению смежных сторон на высоту.

27. Площадь параллелограмма можно найти…

-умножив все его стороны между собой;

-сложив все стороны между собой;

+умножив его основание на высоту;

-половине произведения его основания на высоту.

28. Дан рисунок. Площадь данного треугольника:

29. Площадь прямоугольного треугольника можно найти…

+перемножив катеты между собой и поделив это число на два;

-перемножив все катеты между собой;

-перемножив гипотенузу и катеты между собой;

-перемножив все катеты между собой и разделив это число на три.

30. В трапеции площадь находится так:

-стоит взять половину значения высоты трапеции и умножить его на одно из оснований;

-нужно умножить половину произведения сторон на высоту трапеции;

+следует взять высоту трапеции и помножить это число на половину суммы ее оснований;

-нужно перемножить основания на высоту.

31. Продолжить высказывание: гипотенуза, возведенная в квадрат, равна…

+сумме катетов, каждый из которых возведен в квадрат;

-половине произведения катетов;

32. Отношение отрезков – это…

+отношение их длин;

-произведение их длин;

-половина суммы их длин.

33. Соотношение сходственных сторон подобных треугольников записывается как…

34. Отношение площадей подобных треугольников равно…

+коэффициенту подобия, возведенному в квадрат;

— коэффициенту подобия, взятого в третьей степени;

-коэффициенту подобия в двойном размере.

35. Какой из вариантов содержит первый признак подобия треугольников?

+в треугольнике два угла одного из треугольников равны двум углам оставшегося треугольника;

-если две стороны одного из треугольников равны двум сторонам другого треугольника;

-если три стороны одного треугольника подобны трем сторонам другого треугольника;

-две стороны и угол между ними одного треугольника подобны двум сторонам и углу между ними второго треугольника.

36. Стоит указать вариант, содержащий часть второго признака подобия треугольников.

-если три стороны одного из двух треугольников пропорциональны трем сторонам другого треугольника;

+две стороны треугольника пропорциональны двум сторонам другого треугольника;

-если две стороны и угол между ними одного из двух треугольников пропорциональны тем же элементам в другом треугольнике;

-одна из сторон треугольника пропорциональна такой же стороне второго треугольника.

37. Нужно выбрать вариант, содержащий третий признак подобия треугольников.

+три стороны треугольника пропорциональны тем же сторонам другого треугольника;

-три стороны треугольника пропорциональны двум сторонам другого треугольника;

-три стороны одного из треугольников пропорциональны трем углам другого треугольника;

-две стороны и угол между ними одного треугольника пропорциональны таким же элементам другого треугольника.

38. Отрезок, который проходит через середины двух противоположных сторон, принято называть…

39. Отношение противолежащего катета к гипотенузе это …острого угла.

40. Отношение прилежащего катета к гипотенузе это …острого угла.

41. Отношение противолежащего катета к прилежащему это…острого угла.

42. Дана окружность и прямая. Известно, что от центра окружности до прямой расстояние меньше радиуса. Какой вывод напрашивается?

+прямая и окружность будут содержать две общие точки;

-окружность и прямая содержат лишь одну общую точку;

-прямая и окружность не будут содержать общих точек;

-никакой вывод не напрашивается.

43. Имеется окружность и прямая. Известно так же, что расстояние от центра окружности до имеющейся прямой равно радиусу. Какой вывод стоит сделать?

-никакой вывод делать не надо;

-прямая не пересекается с окружностью;

+прямая с окружностью имеют лишь одну общую точку;

-у прямой и окружности будет две общие точки.

44. В заданной окружности известен радиус и расстояние до определенной прямой. Расстояние до этой прямой больше радиуса. Что можно об этом сказать?

+ они не имеют общих точек;

-они имеют три общие точки;

-они имеют бесконечное множество точек;

-имеется лишь одна точка пересечения.

45. Как называется прямая, имеющая с окружностью лишь одну общую точку?

46. Угол с вершиной в центре окружности это…

47. Если все стороны многоугольника окружности хоть как-то касаются, то этот многоугольник…

48. Направленный отрезок, то есть в котором известно, что является началом, а что концом, это…

49. Длиной вектора является…

+величина отрезка, сопоставляемого вектору;

-любое целое число;

-любое не целое число;

-величина любого отрезка.

50. Когда два вектора равны?

-два вектора равны в любом случае;

+векторы равны, если они имеют одинаковую длину и направлены в одну сторону;

-векторы никогда не бывают равны;

-два векторы равны, если они являются направленными в одну сторону.

51. Два вектора называются коллинеарными, если они…

+лежат либо на одной прямой, либо на параллельных прямых;

-лежат на параллельных прямых;

-лежат на одной прямой;

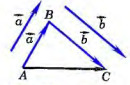
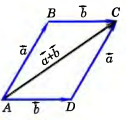
52. Есть рисунок. Какой отрезок отображает сумму векторов а → + b → ?

-нужны дополнительные построения.

53. Дан рисунок. Какое правило здесь проиллюстрировано?

-правило прямоугольного треугольника;

54. Имеется рисунок. Какое правило здесь проиллюстрировано?

55. Разностью векторов а → и b → называется такой вектор…

+сумма с которым b → равна вектору а → ;

— разность с которым b → равна вектору а → ;

-произведение с которым b → равна вектору а → ;

-нет подходящего варианта.

56. Если нужно умножить определенный вектор на число, что получится в итоге?

-всё так и останется;

-длина вектора останется прежней;

-длина вектора увеличится вдвое;

+длина вектора увеличится на то число, на которое умножен вектор.

🔍 Видео

Геометрия 8 класс. Урок 1. Четырехугольник и его элементыСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Четырёхугольник и его элементы Геометрия 8клСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

3 задание ОГЭ. 11299052. Числовые неравенства, координатная прямаяСкачать

Разбор ОГЭ по Математике 2024. Вариант 18 Ященко. Куценко Иван. Онлайн школа EXAMhackСкачать

SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

ЕГЭ Математика Задание 6#27935Скачать

8 класс, 4 урок, ПараллелограммСкачать

Задание 3 ЕГЭ профиль #121Скачать

ОГЭ-2022. ЯЩЕНКО, 36-ВАРИАНТОВ. ВАРИАНТ-17, ЧАСТЬ-1Скачать

6-1*0+2/2 КАКОЙ ПРАВИЛЬНЫЙ ОТВЕТ?Скачать

Решение ВПР математика 7 класс Вариант 2. Разбор всех задач с объяснениями. ФИОКО, СтатГрад. Ященко.Скачать

Задание 19 ОГЭ вариант №86Скачать

ВСЯ геометрия для ОГЭ (Планиметрия для ЕГЭ). Вспоминаем/закрепляем/изучаем. Ультимативный материал💪😎Скачать

ЗАДАНИЕ 8 из ЕГЭ_50Скачать