В окружности проведены две параллельные хорды

Ваш ответ

решение вопроса

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,900
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Отрезки и прямые, связанные с окружностью. Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Свойства хорд и дуг окружности

Теоремы о длинах хорд, касательных и секущих

Доказательства теорем о длинах хорд, касательных и секущих

Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках

Фигура	Рисунок	Определение и свойства
Окружность
Круг
Радиус
Хорда
Диаметр
Касательная
Секущая

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Свойства хорд и дуг окружности

Фигура	Рисунок	Свойство
Диаметр, перпендикулярный к хорде		Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды		Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды		Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности		Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины		Большая из двух хорд расположена ближе к центру окружности.
Равные дуги		У равных дуг равны и хорды.
Параллельные хорды		Дуги, заключённые между параллельными хордами, равны.

Диаметр, перпендикулярный к хорде

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Равные хорды

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Хорды, равноудалённые от центра окружности

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Две хорды разной длины

Большая из двух хорд расположена ближе к центру окружности.

Равные дуги

У равных дуг равны и хорды.

Параллельные хорды

Дуги, заключённые между параллельными хордами, равны.

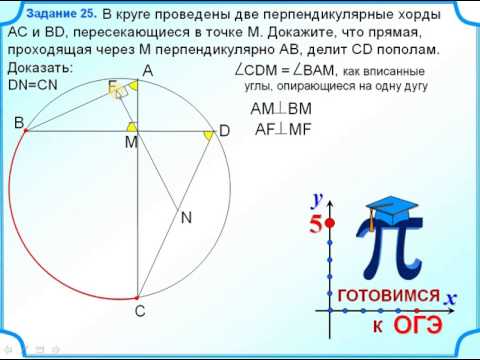
Теоремы о длинах хорд, касательных и секущих

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Фигура	Рисунок	Теорема
Пересекающиеся хорды
Касательные, проведённые к окружности из одной точки
Касательная и секущая, проведённые к окружности из одной точки
Секущие, проведённые из одной точки вне круга

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Пересекающиеся хорды

Касательные, проведённые к окружности из одной точки

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Пересекающиеся хорды

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Касательные, проведённые к окружности из одной точки

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Доказательства теорем о длинах хорд, касательных и секущих

Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).

Тогда справедливо равенство

Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).

Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство

Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).

Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).

Точка B – точка касания. В силу теоремы 2 справедливы равенства

откуда и вытекает требуемое утверждение.

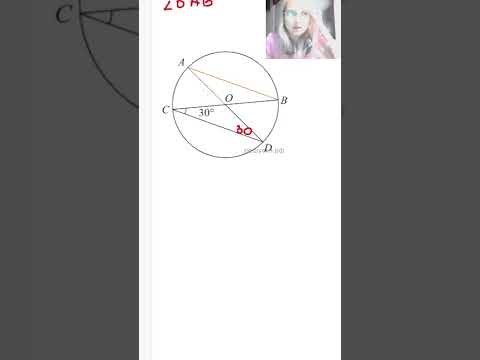
Теорема о бабочке

Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.

Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:

Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим

Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим

Воспользовавшись теоремой 1, получим

Воспользовавшись равенствами (1) и (2), получим

Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство

откуда вытекает равенство

что и завершает доказательство теоремы о бабочке.

В окружности проведены две параллельные хорды, стягивающие дугу в 90°?

Геометрия | 5 — 9 классы

В окружности проведены две параллельные хорды, стягивающие дугу в 90°.

Длина одной из них 10 см.

Найдите расстояние между хордами.

Центральный угол, опирающийся на дугу 90°, равен 90°.

Следовательно, треугольник АОВ прямоугольный.

Высота из прямого угла к гипотенузе равна половине этой гипотенузы.

Расстояние между двумя параллельными прямыми — это перпендикуляр, опущенный из любой точки одной прямой на другую.

Продолжим высоту (перпендикуляр) МО до пересечения с хордой СD в точке N.

ОN — высота прямоугольного прямоугольника COD, равного треугольнику АОВ (по двум катетам — радиусам).

Значит OM = ON = 5см, а MN = 10см.

Отвкт : расстояние между хордами равно 10см.

Рассматриваем треугольник АВС — прямоугольный (АС диаметр), равнобедренный (ВО — высота и медиана).

Следовательно АВ (расстояние между хордами) — 10 см.

СРОЧНО?

В круге радиуса r проведены по одну сторону от центра две параллельные хорды, одна из которых стягивает дугу в 120 градусов.

Найдите часть площади круга заключённую между хордами.

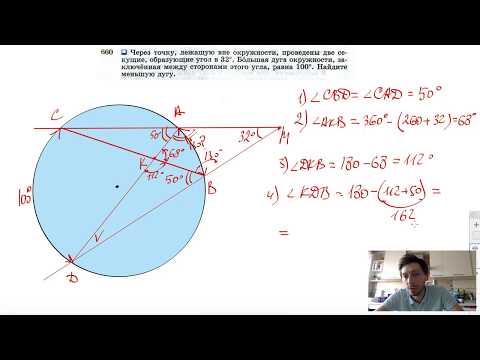
В круге радиуса R проведены по одну сторону центра две параллельные хорды, из которых одна стягивает дугу в 120°, а другая в 60°?

В круге радиуса R проведены по одну сторону центра две параллельные хорды, из которых одна стягивает дугу в 120°, а другая в 60°.

Определить часть площади круга, заключённую между хордами.

В окружности длиной 54П проведена хорда, стягивающая дугу в 150 градусов?

В окружности длиной 54П проведена хорда, стягивающая дугу в 150 градусов.

Вычислите длину дуги и хорды, стягивающей ее.

В окружности с диаметром 30 см проведены две параллельные хорды, длина каждой из которых равна 18 см?

В окружности с диаметром 30 см проведены две параллельные хорды, длина каждой из которых равна 18 см.

Найдите расстояние между хордами помогите, срочно.

Хорда окружности, равная 12корней из 2 см, стягивает дугу в 90градусов?

Хорда окружности, равная 12корней из 2 см, стягивает дугу в 90градусов.

, найдите радиус окружности.

Пусть a — хорда окружности, стягивающая дугу в 90градусов.

В круге радиуса R проведены по одну сторону центра две параллельные хорды, из которых одна стягивает дугу в 120°, а другая в 60°?

В круге радиуса R проведены по одну сторону центра две параллельные хорды, из которых одна стягивает дугу в 120°, а другая в 60°.

Определить часть площади круга, заключённую между хордами.

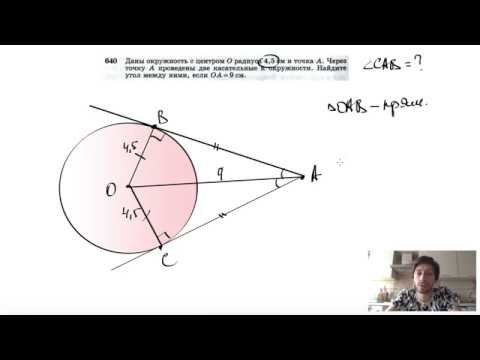
В окружности длиной 75пи, проведена хорда, стягивающая дугу в 120 градусов?

В окружности длиной 75пи, проведена хорда, стягивающая дугу в 120 градусов.

Вычислите длину дуги и хорды.

В окружности длиной 75 * Пи проведена хорда, стягивающая дугу в 120 градусов?

В окружности длиной 75 * Пи проведена хорда, стягивающая дугу в 120 градусов.

Вычислите длину хорды , стягивающая ее.

Хорда окружности равна 3 корень из 2 и стягивает дугу в 90 градусов?

Хорда окружности равна 3 корень из 2 и стягивает дугу в 90 градусов.

Найдите длину дуги и окружности.

Хорда окружности равна 6 корень из 2 дм и стягивает дугу в 90 градусов?

Хорда окружности равна 6 корень из 2 дм и стягивает дугу в 90 градусов.

Найдите длину окружности и длину дуги.

На этой странице сайта размещен вопрос В окружности проведены две параллельные хорды, стягивающие дугу в 90°? из категории Геометрия с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 5 — 9 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

Сумма двух смежных чисел 180 градусам. X + (x + 24) = 180 2x = 156 x = 78 — 1 угол. 180 — 78 = 102 — 2 угол.

Можно конечно записать так(это правильно), но смотри, если вы в классе записываете ОТВЕТ как то по — другому то могут спалить(учитель скажет списал(а). Я это по себе знаю.

Точки •C •N вне угла Точки •D •O •B •M •A внутри угла (Но это не совсем точно).

4. а1 б3 в4 5. А1 б4 в3.

М — середина АВ, значит МВ = АВ / 2 Р — середина МВ, значит РВ = МВ / 2 = АВ / 4, тогда АР = 3 / 4 АВ К — середина ВС, значит КС = ВС / 2 Е — середина КС, значит ЕС = КС / 2 = ВС / 4, тогда ВЕ = 3 / 4 ВС N — середина АС, значит NA = АС / 2 G — середи..

Пусть х и у стороны основания тогда площадь равна х * у = 360 квадрат диагонали по т. Пифагора х² + у² = 41² решаем систему уравнений у = 360 / х х² + 129600 / х² = 1681 х⁴ — 1681х² + 129600 = 0 Д = 1681² — 4 * 129600 = 2307361 ; √Д = 1519 х₁ = √((1..

Пусть длина = а, тогжа ширина = а — 4 площадь = ширина * длина а * (а — 4) = 96 а² — 4а = 96 а² — 4а — 96 = 0 а = — 8 а = 12, длина не может быть ответ 12 ширина = 12 — 4 = 8.

Ответ : 16 смОбъяснение : DC = DE + EC = 2 + 3 = 5 см∠ВЕС = ∠АВЕ как накрест лежащие при пересечении параллельных прямых АВ и DC секущей ВЕ, ∠АВЕ = ∠ЕВС, так как ВЕ биссектриса, значит∠ВЕС = ∠ЕВС, а следовательно ΔЕВС равнобедренный с основанием ВЕ и..

Надеюсь правильно решил Удачи.

1 да может так как он проходит между углами ну и наверное 2 т. К. это луч.