Векторы в доказательствах теорем (2 видео)

Векторы: основные определения и понятия

Скалярная величина — величина, которая может быть охарактеризована числом. Например, длина, площадь, масса, температура и т.д.

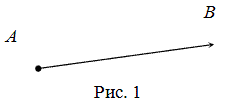
Вектором называется направленный отрезок $overline$; точка $A$ — начало, точка $B$ — конец вектора (рис. 1).

Вектор обозначается либо двумя большими буквами — своим началом и концом: $overline $ либо одной малой буквой: $overline$.

Если начало и конец вектора совпадают, то такой вектор называется нулевым. Чаще всего нулевой вектор обозначается как $overline$.

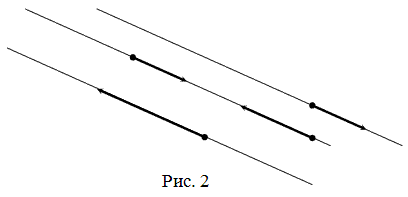
Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых (рис. 2).

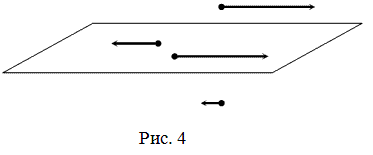
Векторы называются компланарными, если они параллельны одной плоскости или лежат в одной плоскости (рис. 4).

Два вектора всегда компланарны.

Длиной (модулем) вектора $overline $ называется расстояние между его началом и концом: $|overline |$

Подробная теория про длину вектора по ссылке.

Длина нулевого вектора равна нулю.

Вектор, длина которого равна единице, называется единичным вектором или ортом.

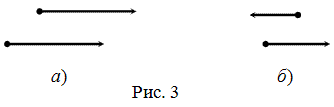
Векторы называются равными, если они лежат на одной или параллельных прямых; их направления совпадают и длины равны.

Иначе говоря, два вектора равны, если они коллинеарны, сонаправлены и имеют равные длины:

В произвольной точке $M$ пространства можно построить единственный вектор $overline$, равный заданному вектору $overline $.

Содержание

Векторный метод в школьном курсе геометрии
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЕ К РЕШЕНИЮ ЗАДАЧ. § 3. Приложение векторов к доказательству теорем и решению задач.
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЕ К РЕШЕНИЮ ЗАДАЧ. § 3. Приложение векторов к доказательству теорем и решению задач
💥 Видео

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Векторный метод в школьном курсе геометрии

Разделы: Математика

Традиционно одной из самых сложных тем школьного курса геометрии является тема “Векторный метод в решении задач”. В то же время понятие вектора является одним из фундаментальных понятий современной математики. Конец XIX и начало XX столетия ознаменовались широким развитием векторного исчисления и его приложений. Будучи материалом математическим, векторный аппарат находит широкое применение в первую очередь в физике и других прикладных науках. Векторный метод является одним из широко употребляемых, красивых и современных методов решения задач, особенно в сочетании с координатным методом.

В данной работе рассмотрены основные свойства векторов, которые следует отнести к векторной алгебре. Приведена классификация задач и приемов их решения с использованием векторного метода.

Целью статьи является не столько пересказ учебного материала, отраженного во всех школьных учебниках геометрии, сколько акцентуация внимания на некоторых вопросах, которые вызывают наибольшую методическую трудность, вопросах, активизирующих мыслительную деятельность обучающихся, могущих послужить основой для небольших учебных исследований.

1. ПОНЯТИЕ ВЕКТОРА.

Термин вектор употребляют в геометрии по крайней мере в двух смыслах. С одной стороны, вектором называют направленный отрезок, с другой стороны, вектор понимают так, как понимают в физике “векторные величины”. Различают соответственно “конкретный вектор” – направленный отрезок и “абстрактный (или, как принято говорить, свободный) вектор”.

Направленным отрезком называют отрезок, у которого указан порядок концов, т.е. один конец назван началом, а другой конец – концом этого отрезка. Направленный отрезок называют вектором. Вообще, вместо векторов – направленных отрезков часто рассматривают “векторы” – упорядоченные пары точек: одна точка начало, другая – конец, не исключая их совпадения.

Свободным вектором (или просто вектором) называется абстрактный объект, связанный с равными направленными отрезками тем, что каждый из равных направленных отрезков считается представителем данного свободного вектора, а неравные направленные отрезки представляют собой неравные свободные векторы. Так понимаемый вектор называется свободным потому, что он представляется направленным отрезком независимо от того, от какой точки он отложен. Равные направленные отрезки и представляют один и тот же вектор.

В частности, все нуль–векторы представляют один и тот же нуль–вектор, который обозначается .

Вектор характеризуется направлением и длиной (модулем). Задать вектор, – значит, задать направление и длину. Длина нуль–вектора равна 0, а направления он не имеет. Изображается нуль вектор любой точкой, которая рассматривается, как его начало и конец. Считается, что нулевой вектор параллелен и перпендикулярен любому вектору.

2. ОСНОВНЫЕ ОТНОШЕНИЯ И СВОЙСТВА.

Равные и коллинеарные векторы

Свойства векторов полезно рассматривать в аналогии со свойствами скалярных величин. Например, свойства равных векторов в аналогии со скалярными величинами представлены в следующей таблице:

векторы

скаляры а=арефлексивностьa=bb=aсимметричность, a=b, b=c a=cтранзитивность

Общеизвестно следующее свойство равных веторов: если четырехугольник ABCD – параллелограмм, то .

Введя этот признак, можно озадачить учащихся такими вопросами:

1. О равенстве каких еще векторов, можно говорить применительно к параллелограмму ABСD?
2. Можно ли утверждать, что при наличии пары равных векторов можно получить и другую пару также равных векторов?
3. Можно ли найти равные векторы в каких–либо пространственных телах (например, в параллелепипеде, призме)?

И еще одно свойство: от любой точки можно отложить вектор, равный данному, и притом только один (сравните со свойствами параллельных прямых).

Задача. Как видно из свойств равных векторов, любые два вектора, равных между собой, но не лежащих на одной прямой, принадлежат некоторому параллелограмму. Что можно сказать о векторах, составляющих основания трапеции? Что можно сказать о векторах, принадлежащих основаниям усеченной призмы?

Учащиеся должны продемонстрировать понимание разницы между равными векторами и коллинеарными. К тому же необходимо “увидеть” не только сонаправленные, но и противоположные векторы.

Сумма векторов. Умножение вектора на число.

Рассмотрим свойства суммы также в аналогии со скалярами:

Весьма полезно после этого разобрать, какие из рассмотренных свойств имеют аналогию со свойствами произведения скалярных величин, а какие – нет.

Координаты вектора. Скалярное произведение.

Проекцией v_x вектора на ось х называется длина его составляющей по этой оси, взятая со знаком “+”, если направление вектора совпадает с направлением оси, и со знаком “–” в противном случае. Заметим, что проекция вектора на ось равна длине этого вектора умноженной на косинус угла между вектором и осью.

При разложении вектора на составляющие вдоль осей координат в декартовой системе координат вводится понятие координат вектора как коэффициентов разложения: если то вектор имеет координаты . При этом длина вектора равна

Скалярным произведением двух векторов называется произведение их абсолютных величин на косинус угла между ними: .

В декартовой системе координат скалярное произведение равно сумме произведений соответствующих координат векторов: Весьма полезным при изучении данной темы может оказаться рассмотрение аналогичных определений в трехмерной модели пространства:

3. КЛЮЧЕВЫЕ ЗАДАЧИ ДЛЯ ОТРАБОТКИ ПОНЯТИЙНОГО АППАРАТА И ОСНОВНЫХ ОПЕРАЦИЙ С ВЕКТОРАМИ.

4. ПРИМЕНЕНИЕ ВЕКТОРОВ К РЕШЕНИЮ ЗАДАЧ И ДОКАЗАТЕЛЬСТВУ ТЕОРЕМ

Векторный аппарат используется при доказательстве некоторых теорем и решении многих задач. Сила векторного метода заключается в том, что он позволяет легко делать обобщения, роль которых в математике трудно переоценить. Хотя следует иметь в виду, что векторный метод не является универсальным и к решению некоторых задач может быть неприменим или малоэффективен.

После изучения основных понятий и фактов, целесообразно провести обобщающий урок, результатом которого должна стать следующая таблица, используемая в дальнейшем при решении задач более высокого уровня.

Компонентами умения использовать векторный метод являются следующие умения:

переводить геометрические термины на язык векторов и наоборот (осуществлять переход от соотношения между фигурами на соотношения между векторами и наоборот);
выполнять операции над векторами (находить сумму, разность векторов);
представлять вектор в виде суммы, разности векторов;
преобразовывать векторные соотношения;
переходить от соотношения между векторами к соотношениям между их длинами;
выражать длину вектора через его скалярный квадрат;
выражать величину угла между векторами через их скалярное произведение.

Классифицируем наиболее употребительные задачи, при решении которых применяется векторный метод.

Доказательство параллельности прямых и отрезков.
Задачи на доказательство деления отрезка в данном отношении.
Доказательство принадлежности трех точек одной прямой.
Доказательство перпендикулярности прямых и отрезков.
Задачи на обоснование зависимости между длинами отрезков.
Задачи на вычисление величины угла.

Ключом к решению задач указанных типов является приведенная выше таблица.

5. КЛЮЧЕВЫЕ ЗАДАЧИ, СПОСОБСТВУЮЩИЕ ФОРМИРОВАНИЮ УМЕНИЯ ИСПОЛЬЗОВАТЬ ВЕКТОРНЫЙ МЕТОД.

1) Отрезки АВ и СD параллельны. Записать это соотношение в векторной форме.
2) Точка С принадлежит отрезку АВ и АВ:ВС=m:n. Что означает это на векторном языке?

7.8. Докажите.

Задачи указанных типов формируют умения и навыки, являющиеся компонентами векторного метода решения задач. В процессе решения этих задач вырабатываются критерии использования векторов для доказательства различных зависимостей. Приведем несколько примеров задач, при решении которых использован векторный метод.

Видео:8 класс, 40 урок, Понятие вектораСкачать

ВЕКТОРЫ И ИХ ПРИМЕНЕНИЕ К РЕШЕНИЮ ЗАДАЧ. § 3. Приложение векторов к доказательству теорем и решению задач.

Библиотека учителя математики.
ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ.
СБОРНИК СТАТЕЙ.

В. А. Гусев, Ю. М. Колягин, Г. Л. Луканкин, Д. И. Хан

Видео:Шаталов за одну минуту доказывает теорему, на которую традиционно выделяется 45 минут урока!Скачать

ВЕКТОРЫ И ИХ ПРИМЕНЕНИЕ К РЕШЕНИЮ ЗАДАЧ.
§ 3. Приложение векторов к доказательству
теорем и решению задач

Текст для быстрого ознакомления (формулы и чертежи качественнее отображаются в PDF файле ниже):

Скачать бесплатно в PDF формате «Сборник статей: Преподавание геометрии в 6-8 классах» на странице Учебники Скачать.

В. А. Гусев, Ю. М. Колягин, Г. Л. Луканкин, Д. И. Хан
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЕ К РЕШЕНИЮ ЗАДАЧ.
§ 3. Приложение векторов к доказательству
теорем и решению задач

Понятие вектора, которое нашло широкое распространение в
прикладных науках, явилось плодотворным и в геометрии. Аппарат
векторной алгебры позволил упростить изложение некоторых
сложных геометрических понятий, доказательства некоторых теорем
школьного курса геометрии, позволил создать особый метод
решения различных геометрических задач.

141 Приложение векторов.

1. Применение векторов при доказательстве теорем
В учебных пособиях по геометрии, начиная с 7 класса, уже
используется векторный аппарат при доказательстве некоторых
теорем. К таким теоремам можно отнести следующую: если при
гомотетии с коэффициентом k точки X и ^отображаются на точки
Хг и Уъ то хУ1 = kXY
Из этой теоремы получаем важные свойства гомотетии:
а) при гомотетии с коэффициентом k все расстояния между
точками умножаются на k\
б) гомотетичные фигуры подобны;
в) при гомотетии с положительным коэффициентом каждый луч
отображается на сонаправленный с ним луч. При гомотетии с отрицательным
коэффициентом каждый луч отображается на противоположно
направленный с ним луч (рис. 13).
Из свойства (в) следует, что при гомотетии прямая отображается
на параллельную ей прямую, отрезок — на параллельный ему
отрезок, угол — на конгруэнтный ему угол.
Итак, эта теорема позволяет отнести гомотетию к преобразованиям
подобия (само определение гомотетии в своей формулировке
этого не содержит). Заметим, что с использованием векторов в разделе
о гомотетии и подобии доказывается еще одна теорема: если
отрезки ОАг и ОВ± пропорциональны отрезкам О А и ОБ и лежат
соответственно на лучах О А и 05, то прямые АХ ВХ и АВ параллельны.
Важную роль играют векторы при изучении тригонометрических
функций в 8 классе. Здесь тригонометрические функции sin а и
cos а определяются как координаты точек единичной окружности,
а соотношения между элементами в прямоугольном треугольнике
получаются из рассмотрения формул, связывающих координаты
произвольного и единичного вектора:
ах = | а [ cos а, ау = | а [ sin а.
Пользуясь векторами, можно доказать известные нам теоремы
планиметрии. Так, например, в учебном пособии по геометрии для
6 класса доказана теорема Фалеса. Доказательство ее фактически

142 Приложение векторов.

сводится к осуществлению параллельного
переноса, отображающего точку Аг на
точку Сг .
Следствием из этой теоремы является
теорема о средней линии треугольника (ниже
эта теорема доказана иначе).
Рассмотрим доказательство некоторых
теорем с помощью векторов.
Т е о р е м а 1. Средняя линия треугольника
параллельна его третьей стороне и ее длина равна половине
длины этой стороны.
Д о к а з а т е л ь с т в о . Рассмотрим Д ABC (рис. 14). Пусть
А В = с, ВС = а и АС = Ь, тогда по определению суммы векторов
— > — ► — ►
с + а = Ь. Пусть М и N — середины сторон АВ и ВС A ABC,
тогда
Ш = т+ BN==-AB + -BC^ — + — = -(с+а) = -Ь.
2 2 2 2 2 2
Так как АС = b и MN = —Ь, то MN — —AC.
2 2
Таким образом, MN ff АС, следовательно, [АС] || ШЛ/1. Так
как MN = AC, то |MJV| =1|ЛС|.
Л ^
Т е о р е м а 2. Сумма квадратов длин диагоналей параллелограмма
равна сумме квадратов длин всех его сторон.
Д о к а з а т е л ь с т в о . Пусть ABCD — данный параллелограмм
(рис. 15).
1. Положим АВ = a, AD = b (|/4£| = |CD| = a, AD =
— | ВС = Ь).
V —V — У
2. По определению суммы и разности векторов АС = а + Ь,
DB = а — Ь.
3. Используя свойства скалярного квадрата, получим:
АС2 + DB2 = (а + b)а + (а — Ь)2—а2 + 2а • b + Ь2 + а2 — 2а-

Ь +
+ Ь2 =2а2 + 2Ь2 , т. е. | /4С |2 + | DB |2 = | ЛВ |2 +1 ВС |2 + I CD |2 + #
+ AD\ так как ЛС2 = | AC|2, DB2 — DB j2.
Т е о р е м а 3. Диагонали ромба взаимно перпендикулярны.
Д о к а з а т е л ь с т в о . Пусть ABCD — данный ромб (рис. 16).
1. Введем обозначения: АВ — а, ВС = b Из определения ромба
АВ — DC = a, AD = ВС = Ь. тт» ‘ ^
2. По определению суммы и разности векторов АС = а + Ь,
DB — а — Ь.

143 Приложение векторов.

3. Рассмотрим АС • DB = (а + Ь) х
х (а— Ь) = а2 — Ь2 = а2 — Ь2 (по свойствам
скалярного произведения).
4. Так как стороны ромба равны, то
а = Ь. Следовательно,ЛС • DB — 0. Из последнего
получаем: AC ± DB, т. е. [DB] 1
± [АС].
Т е о р е м а 4. Диагонали в прямоугольнике
имеют равные длины.
Д о к а з а т е л ь с т в о . Пусть ABCD—
данный прямоугольник (рис. 17).
1. Введя обозначения АВ — а и ВС = Ь,
получим: АС = а + b DB — а — Ь.
2. Найдем квадраты длин диагоналей, используя
свойство скалярного произведения:
ЛС2 = |ЛС|2 = (а + Ь? = а2 + 2а • Ь + Г2-
=а2 +Ь2 , так как а- 6 = 0, ибо в прямоуголь-
нике a Lb.
Итак, | ЛС|2 = а2 + Ь2 . Далее, DB2 —
|DB|2 = (а—Ь)2 — а2 — 2а ■ Ь+ Ь2 — а2 + &2, так как а ± Ь.
Следовательно, | ЛС|2 = |£>£|2 = а2 + Ь2 , т. е. |ЛС| = DB.
2. Методика решения геометрических задач с помощью векторов
Введенный в среднюю школу векторный аппарат дает новый
эффективный метод для решения геометрических задач. Подробнее
об этом методе сказано в статье В. А. Гусева и Д. И. Хана «Методика
решения геометрических задач с помощью векторов» (Математика
в школе, 1978, № 3).
По значимости его можно уподобить методу составления уравнения.
Так как этот метод является новым для учащихся, необходимо:
а) заинтересовать учащихся, показав им эффективность его
использования на специально подобранных задачах;
б) обучать учащихся некоторым эвристикам (системе определенных
правил, помогающих найти ключ к решению задачи), которые
помогут создать у них навык в его применении;
в) обучать этому методу на достаточно простых по геометрическому
содержанию задачах, чтобы не отвлекать внимание школьников
на трудности чисто геометрического содержания.
Следует иметь в виду (и впоследствии указать на это учащимся),
что векторный метод не является универсальным, к решению некоторых
задач он может быть неприменим или малоэффективен.
Можно выделить следующие эвристики:

144 Приложение векторов.

Конкретные применения первых трех эвристик читатель может
пронаблюдать при рассмотрении аффинных задач; последних трех
эвристик — при рассмотрении метрических задач.
3. Аффинные задачи.
Хорошо известны те трудности, с которыми сталкиваются учащиеся
и учитель, когда речь идет о решении аффинных задач.

145 Приложение векторов.

Выделим несколько видов аффинных
задач, которые целесообразно
решать с применением векторов.
При этом обращаем внимание
на задачи, в тексте которых
не содержится никаких понятий
векторной алгебры (т. е. чисто геометрические).
Здесь не рассматривается система
задач каждого вида, конкретный
вид иллюстрируется задачами
средней сложности. Вместе g
тем указываются те требования, которые
предъявляются к задачам
данного вида. Следует отметить,
что рассмотренные ниже три вида
задач достаточно распространены
среди тех задач, которые приходится
решать учащимся средней
школы.
К первому виду отнесем задачи,
связанные с доказательством
параллельности некоторых отрезков
и прямых. В задачах этого
типа для решения нужно показать
коллинеарность векторов, изображаемых
некоторыми данными от-
резками, т. е. доказать, что а — kb,
где k — некоторое число. Рассмотрим
решение задач такого вида на
примерах.
3 а д а ч а 1. В плоскости даны четырехугольник A BCD и точка
М. Докажите, что точки, симметричные точке М относительно
середин сторон этого четырехугольника, являются вершинами параллелограмма.
Р е ш е н и е . Пусть ABCD — данный четырехугольник
(рис. 18), a N, Р, Q и R — точки, симметричные точке М относительно
середин [АВ], [ВС], [CD] и [DA].
Согласно «правилу параллелограмма» имеем:
MN = МА + MB, МР = MB + МС, MQ = МС + MD,
MR — MD + МА. (1)
По определению разности векторов:
NR = MR — MN и PQ = MQ — МР.
Так как NR — PQ = (MR — MN) — (MQ — МР), то, используя
равенства (1), убеждаемся, что NR — PQ = 0, т. е. NR =

146 Приложение векторов.

■= PQ. Аналогично доказывается, что NP = RQ. Следовательно,
NR = PQ и NP — RQ, а это значит, что четырехугольник NPQR —
параллелограмм.
З а д а ч а 2. Дан четырехугольник ABCD. Прямая, проведенная
через вершину А параллельно (ВС), пересекает (BD) в точке М,
а прямая, проведенная через вершину В параллельно стороне AD,
пересекает (АС) в точке N. Доказать, что ШЛП || [DC1.
Р е ш е н и е . Для решения задачи достаточно доказать коллинеарность
векторов (рис. 19), т. е. надо доказать, что DC = kMN,
где k — некоторое число. Но векторы DC и MN непосредственно
один через другой не выражаются, т. е. их коллинеарность видна
не сразу. Чтобы убедиться в их коллинеарности, нужно выразить
каждый из этих векторов через некоторые другие векторы. При
этом замечаем следующее: вектор DC легко выражается через векторы
ОС и OD, вектор MN — через векторы ОМ и ON, где О =
= (АС) П (BD). А векторы ОС и ON можно выразить через вектор
АО, векторы OD и О — через вектор ВО. Отношение длин отрезков
диагоналей четырехугольника можно принять равным отношению
чисел: | АО : |0С| = р : q, В0 : D — т : п (1). Тогда можно
выразить вектор DC через АО и ВО последовательными заменами:
DC = ОС — OD = ^АО — -ВО = — (mqAO — npBO).
р т тр
С другой стороны, из параллельности отрезков BE и AD вытекает
| АО : |ОЛП = |DO| : ОВ = п : т (2). Тогда из чертежа и
равенств (2) следует: ON = —АО. Аналогично из параллельности
Л
отрезков AM и ВС следует: |£0| : ОМ = |СО| : | АО = q ‘ р и
ОМ = —ВО. Тогда можно выразить вектор MN через АО и ВО
4 ,
последовательными заменами: MN — ON — ОМ — —— ВО +
т _ , _ «
+ r LAO = — (-пр = BO + mqAO).
п n q
Откуда DC = —MN, что и означает в переводе на геометри-
т р
ческий язык параллельность отрезков MN и DC.
Ко второму виду относятся задачи, в которых доказывается,
что некоторая точка делит отрезок в некотором отношении или,
в частности, является его серединой.
Для доказательства того, что точка С делит отрезок АВ в некотором
отношении АС : СВ = т : п, достаточно:
а) доказать равенство АС = — СВ;
п
б) доказать равенство

147 Приложение векторов.

QC = • QA -f QB,
m + n m + n
где Q— произвольная точка. Доказательство достаточности последнего
пункта (б) несложно:
п q a + + =r. Iq a + Lq b ,
— 1 — п т п > т п
QC.
т + п т + /
*=»- (QC-QA) =-(QB
т п
■QC)^>-AC = -CB,
т п
что и означает, что I АС ]: ] СВ = т
Заметьте, что, проведя доказательство в обратном порядке,
можно убедиться в необходимости условия б) для деления точкой
С отрезка АВ в отношении m : п.
Решим несколько задач этого вида.
3 а д а ч а 3. В произвольном четырехугольнике отрезок, соединяющий
середины диагоналей, проходит через точку пересечения
средних линий. Доказать, что этот отрезок делится ею пополам.
Р е ш е н и е . Тот факт, что точка О (рис. 20) является серединой
отрезка EF, можно доказать различными способами. Наиболее
естественными из них являются:
1) доказать, что ЕР — QF, это означает, что EPFQ — параллелограмм,
и так как [EF] является его диагональю, то она проходит
через точку О и делится ею пополам;
2) доказать, что ЕО — OF;
3) доказать, что Q0 = — (QE+ QF) или NО= -i (NE + NF);
4) доказать, что СО — — (СЕ + CF) или DO — — (DE + DF).

Рассмотрим первый способ
доказательства, который в Данном
случае является и самым
простым.
В треугольнике ABC отрезок
ЕР является средней линией,
откуда ЕР— АВ. В треугольнике
ABD отрезок QF является
средней линией, откуда
QF = —АВ. Это значит, что
2
ЕР = QF, и задача решена.
З а д а ч а 4. В параллелограмме
A BCD сторона AD разделена
на п конгруэнтных частей
и первая точка деление сома

148 Приложение векторов.

единена с вершиной В (рис. 21). На
какие части делит полученная прямая
диагональ АС? ,
Р е ш е н и е . Пусть DC — b,
DA = а и АР = а АС (рис. 21).
Выразим вектор АР двояким об-
разом через векторы а и Ь:
1) АР — а АС — а (Ь —а) =а ф—
— a) —ab—aa
2) АР = АК + КР=—-а + аКВ=—-а + а(-а + Ь)^
п п п I
= а + ab (КР= а КВ, так как А АР К А ВРС).
П
Тогда по теореме о единственности представления вектора через
два неколлинеарных вектора имеем: ———-а— ——1— -= —а 1 4 =» а =—— .
п п + 1
Это значит, что длина отрезка АР составляет (п + 1) часть от длины
отрезка АС. Задача решена.
При решении задач второго вида иногда выбирается произвольная
точка Q плоскости в качестве полюса. При решении задач
второго вида (и вообще при решении задач векторным способом)
находит широкое применение следующая теорема.
Т е о р е м а . Пусть точки Аъ А2 , А3 не лежат на’ одной прямой,
М — четвертая данная точка, a Q — произвольная точка
плоскости. «Если
QM — o^iQ41+PiQ^2+ YiQ^3>
QM— a2 QA-i + P2 Q^4 2+ y%QA 3 ,
то аг = а2 , pi = р2, уг = у2 .
Д о к а з а т е л ь с т в о . Имеем:
QM = а,0Аг+ ^QA,+ y i QA3 J q% + + y q%
QM = a 2 Q Л i+JQA2+j2QA3 J 1 ^ ‘ 1 _
= oc2 Q^1 -j- P2 Q- +я СВ.
1 2 ( m + n ) 2 ( m + n )
Тогда из свойства середины Е отрезка Л^ можно написать:
СЕ = — ( СВ1 + CAJ = — / — С А + — СВ). (5)
2 к 1 и 4 m + n m + n / w
По теореме о делении отрезка в данном отношении имеем:
СР = — СЛ + — СВ. (6)
m + п т + п
Чтобы связать векторы CG, СЕ, СР, преобразуем вектор СЕ:
^ = 1 / E+idll ^ + ^L±ZLdl^. cs) = 1 (СЛ + СВ +
4 /п+л /7г + /г ) 4
+ _!!_ СЛ + — Щ = — (3CG+ СР) = — CG +
m+я т+ п ) 4 4
+ -СР, т. е. C£=-CG + -CP, а так как 1 + 1 = 1,
4 4 4 4 4
то точки £, G, Р принадлежат одной прямой и |£G| :|Р£| = 1 :3.
Задача решена.
Рассмотренные нами виды аффинных задач на плоскости далеко
не исчерпывают всего многообразия этих задач. Но они образуют
самые многочисленные группы задач, что и оправдывает их А специальное
рассмотрение.
4. Метрические задачи
При решении метрических задач использу-
, ется скалярное произведение векторов. Мы
не будем классифицировать эти задачи по
видам, а приведем несколько примеров таких
задач.
3 а д а ч а 7. На основании АВ равнобедренного
треугольника ABC дана точка Р.
Доказать, что |РС|2 = |ЛС|2—АР — ВР.
Выяснить, как изменится формула, если точка
Р расположена на продолжении основания
АВ.
Р е ш е н и е . Запишем требуемое равенст

152 Приложение векторов.

во в векторной форме. Учитывая сонаправленность^векторов ЛР и РВ
(рис. 24), получим: РС=АС2 — АР • РВ (1). Доказательство равенства
(1) и есть решение задачи. Преобразуем правую часть (1): АС2 —
-ЛРх РВ = АС(ЛС + СР)- (PC +СВ) = ЛС2 — АС ■ PC —
— АС • СВ + СР2 — СР • СВ = (ЛС2 — ЛС • PC) — (ЛС х
X СВ + СР- СВ) + СР2 = AC •(AC — PC) — СВ • (ЛС + СР) -f-
+ СР2 = (ЛС» + С?) • (^с — СВ) + СР2 = ЛР • (ЛС — С5) +
+ СР2.
Если теперь вектор СВ’ — ЛС, то ЛС — СВ = СВ’ — СВ —
= ВВ’, но А АВ’В прямоугольный. Таким образом, АР • (АС —
— СВ) = АР • ВВ’ = 0. Следовательно, ЛС2 — ЛР • РВ — СР2,
откуда и вытекает справедливость доказываемого равенства. Исследуем
изменение этого равенства в зависимости от расположения
точки Р на прямой АВ. Если точка Р принадлежит отрезку АВ, то
при переходе от векторного равенства (1) к скалярному равенству
имеем: РС2 = |РС|2= |РС|2, ЛС5 = |ЛС|2= |ЛС|2, АР ■ РВ =
= | ЛР| • | РВcos (ЛР, РВ) = | ЛР| • | РВ| • cos 0° = | ЛР| х
х |РВ|, т. е. |РС|2 = |ЛС|2 — |ЛР| • |РВ|.
Если же точка Р не принадлежит отрезку АВ, то векторы ЛР и
РВ противонаправлены и ЛР • РВ — | ЛР| • | РВ| cos 180° =
= —| Л Р | • | РВ|. Тогда доказываемое равенство имеет вид: | РС|2 =
= |ЛС|2+ | ЛР| • |РВ|. Задача решена полностью.
З а д а ч а 8. Найти сумму квадратов длин медиан треугольника,
если известны его стороны а, b и с.
Р е ш е н и е . Рассмотрим Д ЛВС (рис. 25).
1. Пусть Л В — с, ВС — а, С А — Ь.
2. По определению суммы векторов
AD=c+ BE* а+-, СР=Ь + —
3. Используя свойство скалярного квадрата,
получим:
Ш+Те2+ СР2 = (с- + |) + (а +1) +
+ (^+7 ) = Г2 + с — а + ^ + а* + аЛ +
— > ■ • >
+ 1 2 + Ь 2 + &.;+^. = 1(а2 + &2 + с2) +
4 4 4
= [с — а + b ■ а +& • с]. (1)

153 Приложение векторов.

4. Так как по правилу сложения векторов а + b + с — О, то
(я + b + с)2 = 0. Таким образом, а2 + &2+с2+ 2 [а — с +а • Ь +
+ fc • с] = 0, т. е. а2 + Ь2 + с2 —-> -*■ —► — *=• — -*2■ [с • а + 6 • a + 6 • d
Итак, с — а + Ь — а + Ь * с а 2 + 6 2 + с 2
Подставив полученное значение в равенство (1), получим:
AD* + BE |2 + |CF|2 = |(a2 + b2 + c2),.
так как согласно свойству скалярного квадрата
AD2= | AD I2, ВВ2 = | BE |2, CF2 = CF |2.
З а д а ч а 9. Доказать, что высоты произвольного треугольника
пересекаются в одной точке.
Д о к а з а т е л ь с т в о . 1. Пусть [АР] ± [ВС], [BQ] -L [СА],
где [ЛР] и [BQ]—высоты A ABC и О — точка их пересечения
(рис. 26).
2. Обозначим ОА = а, ОВ = Ь, ОС = с и L — точка пересечения
(ОС) и (ЛВ).
—3.> По определению разности векторов АВ — b — а, ВС = —*■ —> ->
«= с — Ь, СА — а — с.
4. Так как [РА] ± [ВС], то а • (с — Ь) = 0, т. е. а • с = а • Ь.
5. Аналогично, так как [OB] JL [СЛ],
то 6 • (а — с) = 0, т. е. b • с = b • а.
6. Из этих равенств по транзитивности
а • с — b > с (так как а • b = b • а), т. е.
с • (я — 6) = 0.
Последнее означает: [ОС] J_ [ЛВ].
7. Итак, [CL] — высота А ЛВС.
З а д а ч а 10. Для того чтобы диагонали
четырехугольника были взаимно пер-
и с пендикулярны, необходимо и достаточно,
Рис 26 чтобы суммы квадратов длин противоположных
сторон четырехугольника были
равны. Доказать.
Н е о б х о д и м о с т ь . Имеем перпендикулярность
диагоналей ЛС и BD (рис. 27).
Нужно доказать равенство | ЛВ|2+1 CD |2=
= |ВС|2 + |ЛО|2. Здесь можно обойтись
без векторов, используя теорему Пифагора.
В самом деле, |ЛВ|2+ CD2= |ЛО|2 +
+ |ОВ|2+ |СО|2 + |OD2 — (|ЛО|3 Н-
+ | 0£>|2)+ (| ОВ|2+1 ОС|2)-1 ЛО|2+ |ВС|2.
Рис. 27 * Необходимость доказана.

154 Приложение векторов.

Д о с т а т о ч н о с т ь . Имеем равенство
j АВ |2 + J CD )2 = | ВС |2 + | AD |2.
Нужно доказать перпендикулярность диагоналей АС и BD. На
языке векторов это означает доказательство одного из равенств:
а) СА ■ DB = 0; б) ОА • ОВ = 0; в) ОА • DO — 0;
г) СО ■ ОВ = 0; д) СО • DO = 0; е) СО • DB = 0;
ж) ОА • DB = 0; з) ОВ • СА = 0; и) DO • СЛ = 0.
Теперь нужно составить такое равенство, в котором содержа*
лись бы величины |ЛВ|2, |CD|2, |ВС|2, AD2 и члены одного из
равенств, которые нужно доказать.
Для этого прежде всего преобразуем исходное скалярное равенство
АВ2 + CD2 = ВС2 + DA2 (при записи векторов, получаемых
из скаляров, лучше всего соблюдать определенный порядок
букв по определенному выбранному направлению обхода).
Здесь мы замечаем, что можно дополнить суммы до полного квадрата
и рассмотреть первые степени полученных сумм, т. е. приходим
к необходимости сравнения выражений АВ + CD и ВС + DЛ.
Но они в сумме дают нулевой вектор в силу замкнутости четырехугольника
ABCD:
AB + CD + BC + DA = 0& АВ+CD = СВ + ЛОфф
^ (АВ + сЪу = (CBj-f ADf^> | ЛВ|2 +J CD |2 + 2 Л В • CD —
«= | ВС I2 + AD2 + 2 AD • СВфф AB • CD = AD ■ CB&
(AO + OB) (CO + OD) = (M) + OD) (CO + OB) ф=>
« = » л о — с о + л о — о В + о в — с о + о в — о о = л о — с о +
+ л о — о в + о 5 — с о + о 5 — ов (ло • oh— ао ■ дв) +
+ (ОВ ■ СО — OD ■ СО) = 0 « ЛО (OD — 0″В) + СО (ОВ — OD)=
= 0«=* (ОВ — OD) (ОА + СО) = 0 Приложение векторов