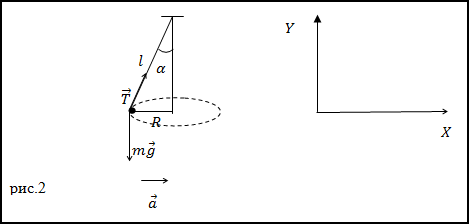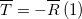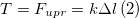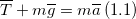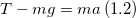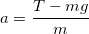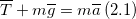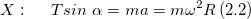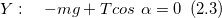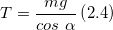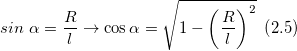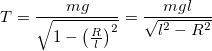Сила натяжения нити по окружности

Видео:Сила натяжения нити (видео 26) | Силы. Законы Ньютона | ФизикаСкачать

Определение и формула силы натяжения нити

Силу натяжения определяют как равнодействующую сил $(bar)$, приложенных к нити, равную ей по модулю, но противоположно направленную. Устоявшегося символа (буквы), обозначающего силу натяжения нет. Ее обозначают и просто $bar$ и $bar$, и $bar$ . Математически определение для силы натяжения нити можно записать как:

где $bar$ = векторная сумма всех сил, которые действуют на нить. Сила натяжения нити всегда направлена по нити (или подвесу).

Чаще всего в задачах и примерах рассматривают нить, массой которой можно пренебречь. Ее называют невесомой.

Еще одним важной характеристикой нити при расчете силы натяжения является ее растяжимость. Если исследуется невесомая и нерастяжимая нить, то такая нить считается просто проводящей через себя силу. В том случае, когда необходимо учитывать растяжение нити, применяют закон Гука, при этом:

где k – коэффициент жесткости нити, $Delta l$ – удлинение нити при растяжении.

Видео:Физика - движение по окружностиСкачать

Единицы измерения силы натяжения нити

Основной единицей измерения силы натяжения нити (как и любой силы) в системе СИ является: [T]=Н

Видео:Определите силу натяжения нити Т1 (Н), если m = 20 кг, T2 = 100 Н.Скачать

Примеры решения задач

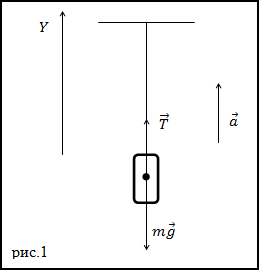
Задание. Невесомая, нерастяжимая нить выдерживает силу натяжения T=4400Н. С каким максимальным ускорением можно поднимать груз массой m=400 кг, который подвешивают на эту нить, чтобы она не разорвалась?

Решение. Изобразим на рис.1 все силы, действующие на груз, и запишем второй закон Ньютона. Тело будем считать материальной точкой, все силы приложенными к центру масс тела.

где $bar$ – сила натяжения нити. Запишем проекцию уравнения (1.1) на ось Y:

Из выражения (1.2) получим ускорение:

Все данные в задаче представлены в единицах системы СИ, проведем вычисления:

Ответ. a=1,2м/с 2

Задание. Шарик, имеющий массу m=0,1 кг прикрепленный к нити (рис.2) движется по окружности, расположенной в горизонтальной плоскости. Найдите модуль силы натяжения нити, если длина нити l=5 м, радиус окружности R=3м.

Решение. Запишем второй закон Ньютона для сил, приложенных к шарику, который вращается по окружности с центростремительным ускорением:

Найдем проекции данного уравнения на обозначенные на рис.2 оси X и Y:

$$ begin X: quad T sin alpha=m a=m omega^ R(2.2) \ Y: quad-m g+T cos alpha=0 end $$

Из уравнения (2.3) получим формулу для модуля силы натяжения нити:

Из рис.2 видно, что:

Подставим (2.5) вместо $cos alpha$ в выражение (2.4), получим:

Так как все данные в условиях задачи приведены в единицах системы СИ, проведем вычисления:

Видео:Введение в силу натяжения нити. Часть 1 (видео 23) | Силы. Законы Ньютона | ФизикаСкачать

Сила натяжения нити и применение формулы в бытовых ситуациях

Силой натяжения называют ту, что действует на объект, сравнимый с проволокой, шнуром, кабелем, ниткой и так далее. Это могут быть несколько объектов сразу, в таком случае сила натяжения будет действовать на них и необязательно равномерно. Объектом натяжения называют любой предмет, подвешенный на все вышеперечисленное. Но кому это нужно знать? Несмотря на специфичность информации, она может пригодиться даже в бытовых ситуациях.

Например, при ремонте дома или квартиры. Ну и, конечно же, всем людям, чья профессия связана с расчетами:

• инженерам;
• архитекторам;
• проектировщикам и пр.

Видео:Обоснуй #1. Невесомая нитьСкачать

Натяжения нити и подобных объектов

А зачем им это знать и какая от этого практическая польза? В случае с инженерами и конструкторами знания о мощи натяжения позволят создавать устойчивые конструкции. Это означает, что сооружения, техника и прочие конструкции смогут дольше сохранять свою целостность и прочность. Условно, эти расчеты и знания можно разделить на 5 основных пунктов, чтобы в полной мере понять, о чем идет речь.

1 Этап

Задача: определить силу натяжения на каждом из концов нити. Эту ситуацию можно рассматривать как результат воздействия сил на каждый конец нити. Она равняется массе, помноженной на ускорение свободного падения. Предположим, что нить натянута туго. Тогда любые воздействия на объект приведет к изменению натяжения (в самой нити). Но даже при отсутствии активных действий, по умолчанию будет действовать сила притяжения. Итак, подставим формулу: Т=м*g+м*а, где g – ускорение падения (в данном случае подвешенного объекта), а – любое иное ускорение, действующее извне.

Есть множество сторонних факторов, влияющих на расчеты – вес нити, ее кривизна и так далее. Для простых расчетов это мы не будем пока что учитывать. Иными словами – пусть нить будет идеальна с математической точки зрения и «без изъянов».

Возьмем «живой» пример. На балке подвешена прочная нить с грузом в 2 кг. При этом отсутствует ветер, покачивания и прочие факторы, так или иначе влияющие на наши расчеты. Тогда мощь натяжения равна силе тяжести. В формуле это можно выразить так: Fн=Fт=м*g, в нашем случае это 9,8*2=19,6 ньютона.

2 Этап

Заключается он в вопросе об ускорении. К уже имеющейся ситуации давайте добавим условие. Суть его в том, чтобы на нить действовало еще и ускорение. Возьмем пример попроще. Представим, что нашу балку теперь поднимают вверх со скоростью 3 м/с. Тогда, к натяжению прибавится ускорение груза и формула примет следующий вид: Fн=Fт+уск*м. Ориентируясь на прошлые расчеты получаем: Fн=19,6+3*2=25,6 ньютона.

3 Этап

Тут уже посложнее, так как речь идет об угловом вращении. Следует понимать, что при вращении объекта вертикально, сила, воздействующая на нить, будет намного больше в нижней точке. Но давайте возьмем пример с несколько меньшей амплитудой качания (по типу маятника). В этом случае для расчетов нужна формула: Fц=м* v²/r. Тут искомое значение обозначает дополнительную мощь натяжения, v – скорость вращения подвешенного груза, а r – радиус окружности, по которому вращается груз. Последнее значение фактически равняется длине нити, пускай она составляет 1,7 метра.

Итак, подставляя значения, находим центробежные данные: Fц=2*9/1,7=10,59 ньютона. А теперь, чтобы узнать полную силу натяжения нити, надо к имеющимся данным о состоянии покоя прибавить центробежную силу: 19,6+10,59=30,19 ньютона.

4 Этап

Следует учитывать меняющуюся силу натяжения по мере прохождения груза через дугу. Иными словами – независимо от постоянной величины притяжения, центробежная (результирующая) сила меняется по мере того, как качается подвешенный груз.

Чтобы лучше понять этот аспект, достаточно представить себе привязанный груз к веревке, которую можно свободно вращать вокруг балки, к которой она закреплена (как качели). Если веревку раскачать достаточно сильно, то в момент нахождения в верхнем положении сила притяжения будет действовать в «обратную» сторону относительно силы натяжения веревки. Иными словами – груз станет «легче», из-за чего ослабнет и натяжение на веревку.

Предположим, что маятник отклоняется на угол, равный двадцати градусам от вертикали и движется со скоростью 1,7 м/с. Сила притяжения (Fп) при этих параметрах будет равна 19,6*cos(20)=19,6*0,94=18,424 Н; центробежная сила (F ц=mv²/r)=2*1,7²/1,7=3,4 Н; ну а полное натяжение (Fпн) будет равняться Fп+ Fц=3,4+18,424=21,824 Н.

5 Этап

Его суть заключается в силе трения между грузом и другим объектом, что в совокупности косвенно влияет на натяжение веревки. Иначе говоря – сила трения способствует увеличению силы натяжения. Это хорошо видно на примере перемещения объектов по шершавой и гладкой поверхностях. В первом случае трение будет большим, поэтому и сдвигать предмет становится тяжелее.

Общее натяжение в данном случае вычисляется по формуле: Fн=Fтр+Fу, где Fтр – трение, а Fу – ускорение. Fтр=мкР, где мк – трение между объектами, а Р – сила взаимодействия между ними.

Чтобы лучше понять данный аспект, рассмотрим задачу. Допустим, у нас груз 2 кг и коэффициент трения равен 0,7 с ускорением движения 4м/с постоянной скорости. Теперь задействуем все формулы и получаем:

1. Сила взаимодействия — Р=2*9,8=19,6 ньютона.
2. Трение — Fтр=0,7*19,6=13,72 Н.
3. Ускорение — Fу=2*4=8 Н.
4. Общая сила натяжения — Fн=Fтр+Fу=13,72+8=21,72 ньютона.

Теперь вы знаете больше и можете сами находить и рассчитывать нужные значения. Конечно, для более точных расчетов нужно учитывать больше факторов, но для сдачи курсовой и реферата этих данных вполне достаточно.

Видео:10.12.20 физика, вес, сила реакции опоры, сила натяжения нити, движение по окружностиСкачать

Видео

Это видео поможет вам лучше разобраться в данной теме и запомнить ее.

Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Вес равен силе натяжения нити

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Определение и формула силы натяжения нити

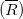
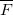
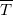
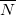
Силу натяжения определяют как равнодействующую сил , приложенных к нити, равную ей по модулю, но противоположно направленную. Устоявшегося символа (буквы), обозначающего силу натяжения нет. Ее обозначают и просто и , и . Математически определение для силы натяжения нити можно записать как:

где 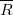= векторная сумма всех сил, которые действуют на нить. Сила натяжения нити всегда направлена по нити (или подвесу).

Чаще всего в задачах и примерах рассматривают нить, массой которой можно пренебречь. Ее называют невесомой.

Еще одним важной характеристикой нити при расчете силы натяжения является ее растяжимость. Если исследуется невесомая и нерастяжимая нить, то такая нить считается просто проводящей через себя силу. В том случае, когда необходимо учитывать растяжение нити, применяют закон Гука, при этом:

где k – коэффициент жесткости нити, 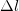– удлинение нити при растяжении.

Видео:Урок 89. Движение по окружности (ч.1)Скачать

Единицы измерения силы натяжения нити

Основной единицей измерения силы натяжения нити (как и любой силы) в системе СИ является: [T]=Н

Видео:Урок 315. Решение задач динамикиСкачать

Примеры решения задач

Задание. Невесомая, нерастяжимая нить выдерживает силу натяжения T=4400Н. С каким максимальным ускорением можно поднимать груз массой m=400 кг, который подвешивают на эту нить, чтобы она не разорвалась?

Решение. Изобразим на рис.1 все силы, действующие на груз, и запишем второй закон Ньютона. Тело будем считать материальной точкой, все силы приложенными к центру масс тела.

где 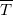– сила натяжения нити. Запишем проекцию уравнения (1.1) на ось Y:

Из выражения (1.2) получим ускорение:

Все данные в задаче представлены в единицах системы СИ, проведем вычисления:

м/с 2

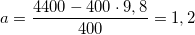
Ответ. a=1,2м/с 2

Задание. Шарик, имеющий массу m=0,1 кг прикрепленный к нити (рис.2) движется по окружности, расположенной в горизонтальной плоскости. Найдите модуль силы натяжения нити, если длина нити l=5 м, радиус окружности R=3м.

Решение. Запишем второй закон Ньютона для сил, приложенных к шарику, который вращается по окружности с центростремительным ускорением:

Найдем проекции данного уравнения на обозначенные на рис.2 оси X и Y:

Из уравнения (2.3) получим формулу для модуля силы натяжения нити:

Из рис.2 видно, что:

Подставим (2.5) вместо в выражение (2.4), получим:

Так как все данные в условиях задачи приведены в единицах системы СИ, проведем вычисления:

Сила натяжения нити равна сумме сил, действующих на резьбу, и напротив их в направлении.

Здесь сила растяжения нити является векторной суммой сил, действующих на нить.

Единицей измерения силы является Н (Ньютон).

Эта формула является следствием третьего закона Ньютона применительно к нити. Если некоторый вес подвешен на нитях, которые находятся в состоянии покоя, то модуль натяжения на резьбе будет равен весу этой нагрузки. Обычно в задачи входят невесомые нерастяжимые нити, которые просто тянут власть через себя, но есть задачи, когда нить растягивается под действием силы. Однако он ведет себя как весна, подчиняясь закону Гука:

Где k – жесткость резьбы, – удлинение нити.

Примеры решения проблем на тему «Натяжная сила нити»

Корпус весом 5 Н подвешен на невесомой растягивающей нити, жесткость которой . Найдите растягивающуюся нить.

Согласно условию, сила натяжения нити равна массе тела, что означает:

Протяженность нити метров.

Два стержня соединены невесомой растягивающей нитью. Сила F действует на первый стержень, приводя оба стержня в направлении, противоположном направлению от первого стержня ко второму. Силы трения, действующие на первый и второй бруски соответственно: и . Жесткость резьбы: k. Найдите удлинение нити.

Обратите внимание, что силы трения действуют на стержни в направлениях, противоположных направлению движения. Нам нужно найти значение сил, растягивающих нить, которая соединена с стержнями. Со стороны первого стержня сила действует на резьбу , поскольку направлена на сжатие нити, а F – при растяжении. Со стороны второго стержня действует сила F. Следовательно:

В любой механической системе присутствует ограниченный набор сил и взаимодействий.

Основные силы в механике:

1. Закон всемирного тяготения (рис. 1):

Рис. 1. Закон всемирного тяготения

Или в случае модуля силы:

• где

• — сила взаимодействия между телами, обладающими массу
• , — массы взаимодействующих тел
• — расстояние между центрами взаимодействующих тел.

Направление: по линии, соединяющей взаимодействующие тела.

Возникает: данная сила возникает при взаимодействии любых массовых частиц (рис. 1).

Используется: в задачах, в которых одно из тел (или оба) являются планетами и/или спутниками.

2. Сила тяжести в рамках Земли (рис. 2).

Рис. 2. Сила тяжести

Представим себе, что в законе всемирного тяготения (1) взаимодействуют Земля и тело вблизи поверхности Земли.

• — масса Земли
• — масса тела вблизи поверхности Земли
• — средний радиус Земли

Тогда . Т.к. масса Земли, средний радиус Земли и гравитационная постоянная — величины известные, то посчитаем:

м/ . Давайте назовём эту константу через м/ . Мы аналитически получили ускорение свободного падения.

Таким образом, сила гравитационного притяжения для тела на Земле мы можем представить как:

Направление: всегда к центру Земли.

Возникает: при взаимодействии любого тела вблизи поверхности Земли и самой Земли.

Используется: в задачах, в которых тело находится вблизи поверхности Земли.

Рис. 3. Сила нормальной реакции опоры

3. Сила нормальной реакции опоры. Данная сила возникает при взаимодействии тела с опорой (тело лежит или движется по опоре). Обычно обозначается . Направление данной силы — перпендикуляр к опоре (рис. 3).

Направление: всегда перпендикулярно опоре.

Возникает: при касании тела любой поверхности (стол, стена).

Используется: в задачах, в которых тело движется или покоится, взаимодействуя с опорой.

Рис. 4. Сила трения

4. Сила трения (рис. 4). Сила трения — сила, возникающая при движении (скольжении) одного тела относительно другого. Физически, данная сила возникает в связи с механическими «цепляниями» неоднородностей (шероховатостей) поверхностей одного тела за неоднородности другого. Данная сила всегда направлена против текущего движения (против скорости).

Для описания силы трения вводят коэффициент трения . Данный коэффициент описывает степень взаимодействия системы тело-подложка. Коэффициент имеет ограничения: . При сила трения отсутствует.

Также в задаче могут быть фразы «силы трения нет», «гладкая поверхность», «силами трения пренебречь». Всё это говорит об отсутствии силы трения.

Нахождению силы трения способствует соотношение:

Направление: против скорости.

Возникает: при скольжении тела относительно негладкой (шероховатой) поверхности.

Используется: в задачах, в которых тело движется (увлекается в движение) относительно поверхности (сама поверхность при этом негладкая).

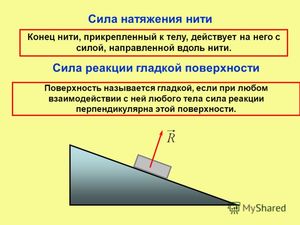
Рис. 5. Сила натяжения нити

5. Сила натяжения нити. Сила натяжения нити — сила, действующая на тело со стороны привязанной к нему нити (рис. 5). Направлена всегда вдоль нити.

Направление: по линии нити.

Возникает: данная сила возникает при наличии в задаче нити.

Используется: в задачах, в которых присутствует нить (при этом за неё обычно тянут). В большинстве таких задач несколько тел связаны невесомой нерастяжимой нитью.

6. Сила растяжения/сжатия (закон Гука, сила упругости). Возникает в деформированном теле, стремится возвратить тело в изначальную форму. Направлена против деформации. Пусть тело под действием некой силы удлинилось на величину (рис. 6).

Рис. 6. Сила упругости

Тогда сила упругости, возникшая в теле:

• где

• — модуль Юнга (табличная величина, характеризующая материал тела)
• — площадь поперечного сечения тела
• — начальная длина тела.

Направление: против деформации тела.

Возникает: при деформации тела.

Используется: в задачах, где тело (пружина) деформирована. Часто деформация задаётся удлинением тела.

7. Силы, заданные задачей. В задаче может присутствовать ряд сил, которые будут описаны в тексте. Чаще всего это силы, вызывающие движение (сила тяги мотора) или тормозящие (силы сопротивления воздуха, воды).

Вывод: для огромного ряда задач на динамику, при использовании второго закона Ньютона, необходимо знать, какие силы действуют на выбранное тело. Анализируя приведенные силы, условия их возникновения и направление действия, можно легко решить поставленную задачу.

🌟 Видео

2.3. Силы упругости. Закон Гука. Сила натяжения нити | Динамика | Александр Чирцов | ЛекториумСкачать

Физика 10 класс : Динамика движения по окружностиСкачать

#1 ТЕОРИЯ. СИСТЕМЫ БЛОКОВ, СИЛА НАТЯЖЕНИЯ НИТИ.Скачать

Движение тел по окружностиСкачать

Выполнялка 50. Движение тела по окружностиСкачать

Урок 87. Движение по наклонной плоскости (ч.1)Скачать

Урок 90. Движение по окружности (ч.2)Скачать

9 класс | Динамика | Движение по окружности. Часть 1Скачать

Математика это не ИсламСкачать

Как определить силу натяжения? #global_ee #егэфизика #огэфизикаСкачать