Геометрия | 5 — 9 классы
Одна окружность вписана в прямоугольную трапецию, а вторая касается большей боковой стороны и продолжений оснований 1)Доказать, что расстояние между центрами окружностей равно большей боковой стороне трапеции 2)Найти расстояние от вершины одного из прямых углов трапеции до центра второй окружности, если точка касания первой окружности с большей боковой стороной делит ее на отрезки , равные 2 и 50.
Распишите пожалуйста подробно!
Окружности будут равные, т.
К. их диаметры равны, как отрезки параллельных прямых, заключенные между параллельными основаниями трапеции))
центры окружностей расположены на биссектрисах соотв углов : CO1, DO1, CO2, DO2
CO1 _|_ DO1 как биссектрисы углов, сумма которых = 180 градусов)))
аналогично CO2 _|_ DO2
CO2DO1 — — прямоугольник, диагонали прямоугольника равны : CD = O1O2
радиус окружностей можно найти из прямоугольного треугольника, построив еще одну высоту трапеции)))
отрезки касательных к окружности, проведенныхиз одной точки, равны))).
- В прямоугольно трапеции один из углов равен 60 градусам, а большая боковая сторона равна 8 см?
- Центр вписанной в равнобедренную трапецию окружности отдален от одной из его вершин на 6 см?
- Точка касания окружности, вписанной в прямоугольную трапецию, делит большую боковую сторону на отрезки длинной 3 см и 12 см?
- Расстояние от центра вписанной в прямоугольную трапецию окружности до концов большей боковой стороны, равны 6 и 8?
- Помогите пожалуйстаВ прямоугольную трапецию вписана окружность?
- Центр окружности описанной около трапеции лежит на ее большем основании?
- Одно из оснований равнобедеренной трапеции равно 4?
- Расстояние от центра вписанной в прямоугольную трапецию окружности до концов большой боковой стороны равны 6 см и 8 см?
- Окружность вписанная в прямоугольную трапецию , делит точкой касания большую боковую сторону на отрезки длиной 25 и 36 см ?
- В прямоугольной трапеции точка касания вписанной окружности делит большую боковую сторону на отрезки 9 см 16 см?
- Одна окружность вписана в прямоугольную трапецию
- Узнать ещё
- В прямоугольную трапецию вписана окружность
- 🎬 Видео
Видео:Геометрия В прямоугольную трапецию вписана окружность. Точка касания делит большую боковую сторонуСкачать

В прямоугольно трапеции один из углов равен 60 градусам, а большая боковая сторона равна 8 см?
В прямоугольно трапеции один из углов равен 60 градусам, а большая боковая сторона равна 8 см.
Найти основание трапеции и радиус вписанной в нее окружности.
Видео:Геометрия В прямоугольную трапецию вписана окружность. Найдите её радиус, если основания трапецииСкачать
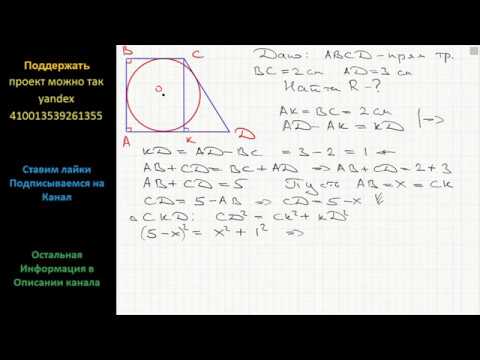
Центр вписанной в равнобедренную трапецию окружности отдален от одной из его вершин на 6 см?
Центр вписанной в равнобедренную трапецию окружности отдален от одной из его вершин на 6 см.
Найдите периметр трапеции если точка касания окружности делит боковую сторону трапеции в отношении 9 и 16.
Видео:Геометрия В прямоугольную трапецию вписана окружность радиуса 12 см Большая из боковых сторон точкойСкачать

Точка касания окружности, вписанной в прямоугольную трапецию, делит большую боковую сторону на отрезки длинной 3 см и 12 см?
Точка касания окружности, вписанной в прямоугольную трапецию, делит большую боковую сторону на отрезки длинной 3 см и 12 см.
Найдите площадь трапеции.
Видео:Геометрия В прямоугольную трапецию вписана окружность. Точка касания делит большую боковую сторонуСкачать

Расстояние от центра вписанной в прямоугольную трапецию окружности до концов большей боковой стороны, равны 6 и 8?
Расстояние от центра вписанной в прямоугольную трапецию окружности до концов большей боковой стороны, равны 6 и 8.
Найти площадь трапеции.
Видео:Геометрия В прямоугольную трапецию вписана окружность. Точка касания делит большую боковую сторонуСкачать

Помогите пожалуйстаВ прямоугольную трапецию вписана окружность?
В прямоугольную трапецию вписана окружность.
Большая боковая сторона точкой касания делится на отрезки 9см и 16см.
Найти площадь трапеции.
Видео:Геометрия В равнобокую трапеция вписана окружность Одна из ее боковых сторон точкой касания делитсяСкачать

Центр окружности описанной около трапеции лежит на ее большем основании?
Центр окружности описанной около трапеции лежит на ее большем основании.
Боковая сторона трапеции равна 15 радиус окружности 12.
5. найдите площадь трапеции.
Видео:ЕГЭ ВПИСАННАЯ ОКРУЖНОСТЬ В ПРЯМОУГОЛЬНУЮ ТРАПЕЦИЮ | ЗАДНИЙ ХОД В МАТЕМАТИКЕ ИЛИ КАКОЙ ТО ПОДВОХ |Скачать

Одно из оснований равнобедеренной трапеции равно 4?
Одно из оснований равнобедеренной трапеции равно 4.
Найдите расстояние между точками касания с её боковыми сторонами вписанной в трапецию окружности радиуса 4.
Видео:Геометрия Точка касания окружности, вписанной в прямоугольную трапецию, делит ее меньшее основаниеСкачать
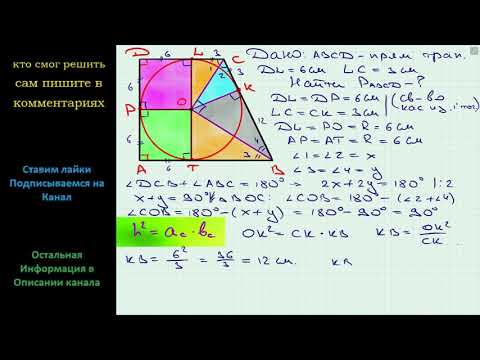
Расстояние от центра вписанной в прямоугольную трапецию окружности до концов большой боковой стороны равны 6 см и 8 см?
Расстояние от центра вписанной в прямоугольную трапецию окружности до концов большой боковой стороны равны 6 см и 8 см.
Найдите площадь трапеции.
Видео:Задание 16 ОГЭ по математике. Окружность вписана в трапецию.Скачать

Окружность вписанная в прямоугольную трапецию , делит точкой касания большую боковую сторону на отрезки длиной 25 и 36 см ?
Окружность вписанная в прямоугольную трапецию , делит точкой касания большую боковую сторону на отрезки длиной 25 и 36 см .
Найдите радиус окружности.
Видео:Простая, но очень противная задача на окружности из ЕГЭ | Планиметрия 83 | mathus.ru #егэ2024Скачать

В прямоугольной трапеции точка касания вписанной окружности делит большую боковую сторону на отрезки 9 см 16 см?
В прямоугольной трапеции точка касания вписанной окружности делит большую боковую сторону на отрезки 9 см 16 см.
Найдите площадь трапеции.
Если вам необходимо получить ответ на вопрос Одна окружность вписана в прямоугольную трапецию, а вторая касается большей боковой стороны и продолжений оснований 1)Доказать, что расстояние между центрами окружностей равно большей боковой стороне ?, относящийся к уровню подготовки учащихся 5 — 9 классов, вы открыли нужную страницу. В категории Геометрия вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.
Диагонали параллелограмма точкой пересечения делятся пополам. MO = ON, BO = OD AM = NC = > AM + MO = ON + NC AO = OC Если в четырехугольнике диагонали точкой пересечения делятся пополам, то четырехугольник — параллелограмм. AO = OC, BO = OD = > ABC..
Т. ADB равен т. CBD т. К они равносторонние углы и стороны одинаковы а угол 1 равен углу 2 т. К они вертикальные.
Решение дано на фото.
ABCD — ромб ; BD = 60 ; O — точка пересечения диагоналей ; OA = OC = √(50² — (60 / 2)²) = 40AC = OA = 80S(ABCD) = (1 / 2)·AC·BD = 2400h = 2r = S(ABCD) / AB = 48r = h / 2 = 24.
Решение в приложении.
Бок ст — x основ — 2x 2x + 2x = 66, 5 4x = 66, 5 x = 16, 625 (см) — бок ст основ — 33, 25 см.
Медиана делит треугольник на два треугольника равной площади. S ABM = S ABC / 2 = 96 / 2 = 48 (см ^ 2) AM = AC / 2 = 20 / 2 = 10 (см) S ABM = AM * BH / 2 BH = 2 * S ABM / AM = 2 * 48 / 10 = 9, 6 (см) AH = √(AB ^ 2 — BH ^ 2) = √(100 — 92, 16) = 2, 8 ..
Из формулы площади тр — ка найдем sinА : S = (1 / 2) * АВ * АС * sin A. Sin A = 2S / 200 = 0, 96. Теперь зная sin A, можно найти cos A : cos A = — кор(1 — sin квад А) = — 0, 28. Здесь знак минус, так как угол А — тупой по условию. Теперь из треуг..
Наверно условие такое : ABCD параллелограмм АК — биссектриса угла BAD, делит сторону ВС на отрезки ВК и КС. Периметр параллелограмма = 42см. Найдите стороны, если ВК : КС = 2 : 3. Тогда : биссектриса угла отсекает от параллелограмма равнобедренный..
Видео:Задача про трапецию, описанную около окружностиСкачать

Одна окружность вписана в прямоугольную трапецию
Одна окружность вписана в прямоугольную трапецию, а вторая касается большей боковой стороны и продолжений оснований.
а) Докажите, что расстояние между центрами окружностей равно большей боковой стороне трапеции.
б) Найдите расстояние от вершины одного из прямых углов трапеции до центра второй окружности, если точка касания первой окружности с большей боковой стороной трапеции делит её на отрезки, равные 2 и 50.
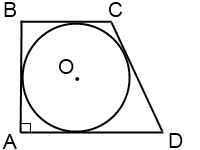
а) Пусть O — центр окружности, вписанной в прямоугольную трапецию ABCD с основаниями AD и BC, O1 — центр окружности, касающейся большей боковой стороны и продолжений оснований трапеции (рис. 1).
Точка O лежит на биссектрисах углов BCD и ADC, следовательно,
Точка O1 лежит на биссектрисе угла, смежного с углом BCD, значит, Аналогично, углы CO1D и ODO1 — прямые. Значит, OCO1D — прямоугольник, поэтому CD = OO1.
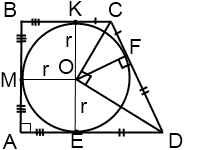
б) Пусть окружность, вписанная в трапецию ABCD, касается стороны AD в точке P, а стороны CD — в точке M, вторая окружность касается прямой AD в точке Q (рис. 2).
Радиусы окружностей OP и O1Q равны половине расстояния между параллельными прямыми AD и BC. Получаем, что OO1QP — прямоугольник, следовательно, OO1 = PQ.
В прямоугольном треугольнике COD имеем:
В прямоугольном треугольнике AQO1 имеем:
Расстояние от вершины прямого угла трапеции до центра второй окружности равно
Ответ:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Видео:Геометрия Точка касания окружности, вписанной в прямоугольную трапецию, делит ее большее основаниеСкачать  Узнать ещёЗнание — сила. Познавательная информация Видео:Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать  В прямоугольную трапецию вписана окружностьЕсли в условии задачи сказано, что в прямоугольную трапецию вписана окружность, можно использовать следующие свойства. 1. Сумма оснований трапеции равна сумме боковых сторон. 2. Расстояния от вершины трапеции до точек касания вписанной окружности равны. 3. Высота прямоугольной трапеции равна ее меньшей боковой стороне и равна диаметру вписанной окружности. 4. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции. 5. Если точка касания делит боковую сторону на отрезки m и n, то радиус вписанной окружности равен И еще два полезных свойства прямоугольной трапеции, в которую вписана окружность: 1) Четырехугольник, образованный центром вписанной окружности, точками касания и вершиной трапеции — квадрат, сторона которого равна радиусу. (AMOE и BKOM — квадраты со стороной r). 2) Если в прямоугольную трапецию вписана окружность, площадь трапеции равна произведению ее оснований. Обозначим CF=m, FD=n. Поскольку расстояния от вершин до точек касания равны, высота трапеции равна двум радиусам вписанной окружности, а 🎬 Видео🔴 В прямоугольной трапеции основания ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать  Планиметрия 27 | mathus.ru | окружность, касающаяся основания трапеции и вписанной в нее окружностиСкачать 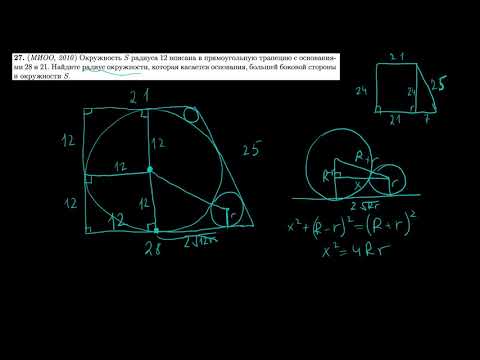 Вписанные и описанные окружности. Вебинар | МатематикаСкачать  Окружность, вписанная в трапециюСкачать  Трапеция. Практическая часть - решение задачи. 8 класс.Скачать  Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать  Задание 26 Описанная прямоугольная трапецияСкачать  |











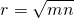
 Площадь трапеции равна произведению полусуммы ее оснований на высоту:
Площадь трапеции равна произведению полусуммы ее оснований на высоту: