2018-05-31 
Показать, что на границе раздела двух сред нормальные составляющие вектора Пойнтинга не терпят разрыва, т. е. $S_ = S_$.
Пусть $vec$ — вдоль оси z. Тогда
Используя граничное условие $E_ = E_, H_ = H_$ на границе ($t = x$ или у), мы видим, что
Видео:Вектор Умова-Пойнтинга ● 3Скачать
Две диэлектрические среды
Определим условия, при которых в случае падения плоской электромагнитной волны на плоскую границу раздела двух идеальных диэлектриков отсутствует преломленная волна, т.е. имеет место полное отражение. Угол преломления θ может изменяться от нуля до π/2. Значение θ = π/2 является предельным. Назовем угол падения φ = φкр, при котором θ = π/2, критическим углом. Полагая во втором законе Снеллиуса θ = π/2, получаем:
(3.24)
Так как sin φкр не может быть больше единицы, полученное равенство возможно лишь в том случае, если k2 φкр синус угла преломления:
становится больше единицы. Этого не может быть при вещественных значениях угла θ. Предположим, что угол θ является комплексным: θ = ξ + iη. Тогда sinθ = sin(ξ + iη) = sinξchη + icosξshη, и для того чтобы выполнялось условие sinθ > l, достаточно считать 
, где п= 0, ±1; ±2. При этом sin ξ = 1, cos ξ = 0, a sinθ = chη > 1 при любом η ≠ 0.
Так как sinθ > 1, то cos θ оказывается чисто мнимой величиной. При этом коэффициенты отражения 
и R||, определяемые формулами (3.16) и (3.21), выражаются как (а ± ib)/(a 
ib),где а и b – действительные числа. Следовательно, по абсолютной величине и R||равны единице и могут быть представлены в форме:
(3.27)
Это означает, в частности, что средняя плотность потока энергии одинакова в падающей и отраженной волнах.
Таким образом, для возникновения полного отражения необходимо выполнение двух условий:
– вторая среда должна быть оптически менее плотной по сравнению с первой (k2 φкр).
Выпишем выражения для поля в первой среде для случая нормальной поляризации. Сложим поля (3.6) и (3.8) и учтем, что в рассматриваемом случае 
. Положим в (3.8) φ1 = φ и вынесем за скобки 
и используя формулы Эйлера, получаем:
(3.28)
(3.29)
Аналогично записывается поле в первой среде в случае параллельно поляризованных волн. Очевидно, что в этом случае вектор 
будет иметь две составляющие 
и 
, а вектор 
– только составляющую 
.
Из полученных формул следует, что в первой среде электромагнитное поле имеет структуру плоской волны, распространяющейся вдоль поверхности раздела (вдоль оси Z), и представляет собой направляемую волну, направление распространения которой определяется (направляется) границей раздела. Поверхности равных фаз образуют семейство плоскостей, перпендикулярных оси Z. Амплитуды векторов Е и Н зависят от координаты х и угла падения φ. Поверхности равных амплитуд образуют семейство плоскостей, перпендикулярных оси X. Так как ПРА и ПРФ не совпадают друг с другом (они образуют взаимно перпендикулярные плоскости), то волна является неоднородной и плоской.
В отличие от плоской волны, свободно распространяющейся в безграничной однородной изотропной среде и всегда являющейся поперечной, в рассматриваемой волне имеются продольные (параллельные направлению распространения) составляющие векторов поля. В случае нормальной поляризации вектор Н имеет как поперечную Нх, так и продольную 
составляющие, а вектор Е целиком лежит в поперечной плоскости. В случае параллельной поляризации, наоборот, вектор Е имеет и продольную Еz,и поперечную Еx составляющие, а вектор Н целиком лежит в поперечной плоскости.
Фазовая скорость рассматриваемой волны:
(3.30)
больше фазовой скорости волны, распространяющейся в однородной среде с параметрами 
но меньше, чем фазовая скорость волны, распространяющейся в однородной среде с параметрами 
Действительно, так как 
, причем 0 1, то выполняются неравенства 
, из которых следует, что:
(3.31)
Из формулы (3.30) видно, что фазовая скорость уменьшается с увеличением угла падения. Ее минимальное значение при 
равно скорости света в первой среде.
Длина волны λz вдоль направления распространения (оси Z) или (что то же самое) длина рассматриваемой направляемой волны Λ вычисляется по формуле:
(3.32)
Она больше длины волны, свободно распространяющейся в первой среде: λ1 = 2π/k1, но меньше, чем длина волны, свободно распространяющейся во второй среде: λ2 = 2π/k2, т.е.
(3.33)
Изменение составляющих векторов Е и Н в первой среде вдоль любой линии, перпендикулярной поверхности раздела (т.е. параллельной оси X), имеет характер стоячей волны (рис. 3.6) с длиной:
(3.34)
Рис. 3.6. Изменение составляющих векторов Е и Н в первой среде вдоль линии, перпендикулярной поверхности раздела
Поперечные составляющие векторов Е и Н изменяются синфазно. Продольная составляющая вектора Н (или Е) сдвинута по фазе относительно поперечных составляющих векторов Е и Н на π/2.
Комплексный вектор Пойнтинга определяется выражением:
(3.35)
Здесь знак «+» соответствует случаю нормальной поляризации, а знак «-» – параллельной поляризации. Постоянная ψ взависимости от типа поляризации падающей волны равна 
или ψ||. Из (3.35) следует, что комплексный вектор Пойнтинга имеет две составляющие Пх и Пz, сдвинутые по фазе на π/2.
Среднее значение вектора Пойнтинга:
(3.36)
Следовательно, в среднем энергия распространяется только в направлении оси Z,т.е. вдоль поверхности раздела. В направлении, перпендикулярном поверхности раздела, существует только реактивный поток энергии.
Имеется бесчисленное множество плоскостей, перпендикулярных оси X, на которых касательная к ним составляющая напряженности электрического поля (Еу в случае нормальной и Ez случае параллельной поляризаций) и нормальная составляющая напряженности магнитного поля тождественно равны нулю (см. рис.3.6). Точки пересечения этих плоскостей с осью X определяются из уравнения 
, где ψ равно или ψ|| в зависимости от поляризации волны. Например, в случае нормальной поляризации:
(3.37)
На таких плоскостях (см. рис.3.6) векторы Е и Н автоматически удовлетворяют условиям, эквивалентным граничным условиям на поверхности идеально проводящего металла. Кроме того, поток энергии (как активный, так и реактивный) через эти плоскости тождественно равен нулю 
Это означает, в частности, что если бы одна из этих плоскостей (например, х = хn) действительно была идеально проводящей, то структура поля над этой плоскостью, т.е. при 
, осталась бы прежней.
Средняя скорость распространения энергии направлена вдоль оси Z. Для ее определения выделим в поле рассматриваемой волны энергетическую трубку (см. раздел 1.8.5 юниты 1), через боковую поверхность которой поток энергии в любой момент времени равен нулю. Например, в случае нормальной поляризации в качестве такой трубки можно выделить объем, заключенный между двумя соседними плоскостями, которые определяются уравнением (3.37). Этот объем может быть произвольно протяженным вдоль оси Y. Так как в пределах поперечного сечения этой трубки значения вектора Пойнтинга П и объемной плотности электромагнитной энергии w зависят от переменной х, то для вычисления скорости переноса энергии нужно воспользоваться формулой (1.161 из юниты 1). При этом получим:
(3.38)
где Пср и wcp – средние за период значения вектора П и w соответственно. Вычисляя входящие в это выражение интегралы, получаем:
(3.39)
Таким образом, скорость распространения энергии меньше скорости света в первой среде.
Из формул (3.30) и (3.39) следует, что произведение фазовод скорости на скорость распространения энергии равно квадрату скорости света в первой среде:
(3.40)
Перейдем к анализу свойств поля, возникающего во второй среде. В случае нормальной поляризации векторы 
и 
определяются формулами (3.9). Так как при полном отражении от границы раздела двух диэлектриков cosθ является мнимой величиной, удобно ввести обозначение:
(3.41)
(3.42)
Подчеркнем, что параметр α при φ>φкр является действительным числом.
Знак «-» при iα в формуле (3.41) выбран из физических соображений (при выборе знака «+» амплитуда поля во второй среде с удалением от границы раздела вдоль оси X будет возрастать до бесконечности, что невозможно).
Учитывая равенство (3.41) и соотношение (3.11), перепишем формулы (3.9) в форме:
(3.43)
Формулы для поля параллельно поляризованной волны записываются аналогично и могут быть получены из выражений (3.43) на основе перестановочной двойственности уравнений Максвелла.
Из формул (3.43) следует, что во второй среде электромагнитное поле имеет структуру плоской неоднородной волны, распространяющейся вдоль оси Z. Поверхности равной фазы (z = const) и равной амплитуды (х = const) взаимно перпендикулярны. Фазовая скорость и длина волны Λ = λz такие же, как в первой среде, и определяются формулами (3.30) и (3.32) соответственно. Имеются продольные составляющие векторов поля (Нz в случае нормальной поляризации и Ez в случае параллельной поляризации). Продольные составляющие сдвинуты по фазе относительно поперечных на π/2.
Вектор Пойнтинга имеет две составляющие Пz и Пх. При этом составляющая Пz является вещественной, а составляющая Пх – чисто мнимой. Это означает, что во второй среде так же, как в первой среде, энергия в среднем распространяется только в направлении оси Z. В направлении, перпендикулярном поверхности раздела, существует только реактивный поток энергии.
Амплитуды векторов поля экспоненциально убывают с удалением от поверхности раздела (см. рис. 3.6). Постоянная α, определяющая скорость этого убывания, зависит от угла падения φ. При φ = φкр постоянная α равна нулю. При изменении угла φ от φкр до π/2 постоянная α возрастает от нуля до 
. Таким образом, при φ > φкр волна во второй среде фактически существует лишь в некотором слое, примыкающем к поверхности раздела, и распространяется вдоль границы раздела. Такая волна называетсяповерхностной.
Для вычисления скорости распространения энергии нужно выбрать энергетическую трубку, на боковой поверхности которой нормальная составляющая вектора Пойнтинга равна нулю. В качестве такой трубки в рассматриваемом случае нужно выбрать объем, протяженный по оси X от х=∞ до первой плоскости, на которой составляющая Пxравна нулю. Эта плоскость расположена в первой среде и пересекает ось X в точке х = (π-ψ)/(2k1соsφ), определяемой из уравнения sin (2k1соsφ + ψ) = 0, где ψ равно 
или ψ|| в зависимости от поляризации падающей волны. Вычисляя vэ по формуле (1.161 из юниты 1), получаем, что скорость распространения энергии во второй среде имеет такое же значение, как и в первой, т.е. определяется выражением (3.39).
Видео:Вектор Умова-Пойнтинга ● 2Скачать
Вектор Пойнтинга (вектор Умова — Пойнтинга)
Перенос энергии бегущей упругой и электромагнитной волной определяют при помощи вектора, который называют вектором потока энергии. Этот вектор обозначим как $overline $(встречается обозначение $overline
$) Он показывает количество энергии, протекающее в волне за единицу времени через единицу площади поперечного сечения волны. Для электромагнитных волн данный вектор был введен Пойнтингом в 1884 г. Скорость переноса энергии при помощи вектора Пойнтинга не изменяется и равна характеристической скорости распространения электромагнитной волны в пространстве. Сейчас данный вектор ($overline$) называют вектором Умова — Пойнтинга.
Видео:Вектор Умова-Пойнтинга ● 1Скачать
Определение
Вектором Умова — Пойнтинга ($overline$) называют физическую величину, определяющую поток энергии электромагнитного поля, который равен:
где $overline$ — напряженность электрического поля; $overline$ — напряженность магнитного поля. Направлен $overline$ перпендикулярно $overline$ и $overline$ и совпадает с направлением распространения электромагнитной волны.
Видео:Вектор Умова Пойтинга или откуда берётся энергия в электромагнетизмеСкачать
Величина вектора Умова — Пойнтинга
Правая часть формулы (1) представляет собой векторное произведение векторов, значит, величина вектора Умова — Пойнтинга для электромагнитной волны равна:
где $alpha $ — угол между векторами $overline$ и $overline$, но $overlinebot $ $overline$, следовательно, получаем для электромагнитной волны:
Вектор $overline $удовлетворяет в свободном пространстве уравнению непрерывности:
где $w$ — объемная плотность энергии электромагнитного поля.
Видео:3.5 Комплексный вектор ПойнтингаСкачать
Вектор Умова — Пойнтинга плоской электромагнитной волны
В случае плоской электромагнитной волны величина вектора $overline$ равна:
где $u$ $=frac<sqrt<_0mu varepsilon _0>>$- фазовая скорость распространения электромагнитного возмущения в веществе с диэлектрической проницаемостью $varepsilon $ и магнитной проницаемостью $mu .$
где $c$ — скорость света в вакууме.
Мгновенные величины напряженности магнитного и электрического полей в рассматриваемой волне связаны соотношением:
выразим напряженность $H$:
Учитывая формулу (8) величину вектора $overline$ запишем как:
В изотропном веществе объемную плотность энергии электромагнитного поля найдем как:
Учитывая формулы (6) и (10) запишем еще одно выражение для величины вектора $overline$:
На практике переходят от мгновенных величин к их средним значениям. Для плоской электромагнитной волны средняя величина по времени вектора Умова — Пойнтинга равна:
Модуль величины $left|_tright|$ называют интенсивностью ($I$) электромагнитной волны:
Направление вектора Умова — Пойнтинга показывает направление движения энергии в электромагнитном поле. Если изобразить линии, касательные к которым в любой точке совпадут с направлениями вектора $overline$, то такие линии будут являться путями распространения энергии электромагнитного поля. В оптике это лучи.
Видео:2.5 Граничные условия для векторов поля на поверхности раздела средСкачать
Примеры задач с решением
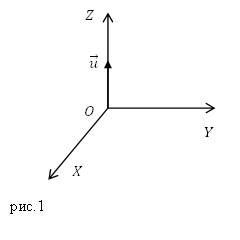
Задание. На рис.1 изображен вектор фазовой скорости плоской электромагнитной волны. В какой плоскости расположены векторы $overline$ и $overline$ полей этой волны?
Решение. Основой решения нашей задачи будем считать определение вектора $overline$:
Вектор $overline$ является результатом векторного произведения векторов$overline$ и $overline$, он направлен в сторону распространения электромагнитной волны, следовательно, $overlineuparrow uparrow overline$, для рис.1 вектор Умова — Пойнтинга направлен по оси Z. Значит, векторы $overlineи overline$ лежат в плоскости XOY.
Ответ. XOY
Задание. Запишите модуль среднего вектора Умова — Пойнтинга электромагнитной волны: $overline=E_0 $Считайте, что волна распространяется в вакууме по оси X.
Решение. Модуль вектора Умова — Пойнтинга для электромагнитной волны:
где $E$ и $H$ — мгновенные значения электрического и магнитного полей. Мгновенное значение вектора Умова — Пойнтинга будет равно:
[S=EH=E_0H_0<^2 left(omega t-kxright)(2.2), >]
где $H_0$ — амплитуда колебаний напряженности магнитного поля.
Средняя величина $_t$ может быть найдена:
принимая во внимание, что $<leftlangle <^2 left(omega t-kxright) >rightrangle >_t=frac$, для вакуума имеем:
📺 Видео
Энергия течёт в пространстве а не в проводе Вектор Умова ПойтингаСкачать
5 Вектор ПойтингаСкачать
5.7 Граничные условия Леонтовича. Поверхностный эффект. Мощность потерь в проводникеСкачать
Лекция №26 "Электромагнитные волны на границе раздела двух сред"Скачать
Вектор Умова-Пойнтинга ● 5Скачать
Вектор Умова-Пойнтинга ● 4Скачать
Вектор Пойнтинга и энергия. ЭНПСкачать
ЧК_МИФ_3_4_4_2_- (L3)___ ВЕКТОР ПОЙНТИНГАСкачать
Билет №38 "Поток энергии"Скачать
5.2 Формулы Френеля для коэффициентов отражения и преломленияСкачать
Лекция №11 "Поляризация. Оптика анизотропных сред"Скачать
Теорема Умова-Пойнтинга, вектор Пойнтинга. Переменное электрическое поле. Пару слов об экзамене.Скачать
5.6 Три режима распространения волны в первой средеСкачать
магнитная защита. Векторы B и H на границе разделаСкачать
