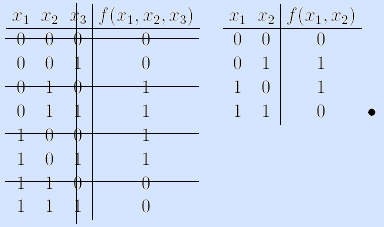Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
- «Снятие эмоционального напряжения у детей и подростков с помощью арт-практик и психологических упражнений»
- Описание презентации по отдельным слайдам:
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Дистанционные курсы для педагогов
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Вес вектора столбца значений функции
- Как определить фиктивную переменную
- Вход в систему
- Навигация
- Последние комментарии
- О существенных и фиктивных переменных булевых функций
- 📸 Видео
Видео:2020.10.20.Лекция 4.Переборные методы подсчёта веса вектора (Сахалин)Скачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»
Сертификат и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Существенные и фиктивные переменные
Определение Говорят, что булева функция f(x1, …, xi, …, xn) существенно зависит от переменной xi, если выполняется условие: f(x1, …, xi-1,0,xi+1, …, xn) ≠ f(x1, …, xi-1,1,xi+1, …, xn). В этом случае также говорят, что переменная xi существенная, в противном случае ее называют фиктивной переменной. Другими словами, переменная является несущественной, если ее изменение не изменяет значения функции
Пример 1. Рассмотрим булеву функцию f(x1, x2, x3) и исследуем ее переменные x1 и x3. Из таблиц истинности видно, что переменная x1 функции f(x1, x2, x3) существенная, так как f(0,x2, x3) ≠ f(1,x2, x3). Переменная x3 фиктивная, так как f(x1, x2, 0) = f(x1, x2, 1).
Алгоритм распознавания фиктивной переменной по таблице истинности. – Для переменной x1 сравниваются половины столбца значений функции: верхняя и нижняя, так как именно в верхней половине x1=0, а в нижней x1=1, если они совпадают, то переменная x1 фиктивна; – для переменной x2 сравниваются четвертины столбца в каждой половине, так как именно в верхних четвертинах x2 =0, а в нижних x2 =1, если четвертины в каждой половине совпадают, то переменная x2 фиктивна; – и так далее (за четвертинами следуют 1/8, 1/16, … ).
Пример 1. Булева функция f(x1, x2, x3) Переменная x1 существенна, так как верхняя половина столбца значений функции (0011) не равна нижней половине (1100). Переменная x2 существенна, так как четвертины уже в первой половине различаются (00 и 11). Переменная x3 фиктивна, так как осьмушки во всех четвертинах равны (0 и 0, 1 и 1, 1 и 1, 0 и 0).
Достаточное условие отсутствия фиктивных переменных Если вес вектора-столбца значений функции нечетен, то функция не может содержать фиктивных переменных.
Алгоритм удаления фиктивной переменной Алгоритм удаления фиктивной переменной xi состоит в вычеркивании из таблицы истинности всех строк, в которых xi = 0 (или всех строк, в которых xi = 1), и столбца xi. Пример (функция та же). Применив алгоритм для удаления фиктивной переменой x3, получаем результат
Пример Определение. Булевы функции назовем равными с точностью до фиктивных переменных, если равны функции, полученные из исходных удалением фиктивных переменных Рассмотрим функции f1(x1, x2) и f2(x1, x2). Удалив фиктивную переменную x1 функции f1(x1, x2) и фиктивную переменную x2 функции f2(x1, x2), получим равные функции f1(x2)=f2(x1)=f(x). Значит, исходные функции равны с точностью до фиктивных переменных.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 942 человека из 79 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 316 человек из 68 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 691 человек из 75 регионов
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 487 729 материалов в базе
Видео:Вектор-функции многих переменных, факультет химии, лекция 21 04 20Скачать

Дистанционные курсы для педагогов
Другие материалы
- 11.12.2016
- 908
- 11.12.2016
- 463
- 11.12.2016
- 434
- 11.12.2016
- 547
- 11.12.2016
- 737
- 11.12.2016
- 759
- 11.12.2016
- 476
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 11.12.2016 2663 —> —> —> —>
- PPTX 501.1 кбайт —> —>
- Рейтинг: 1 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Ялина Янина Викторовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 5 лет и 10 месяцев
- Подписчики: 0
- Всего просмотров: 18351
- Всего материалов: 11
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Работа с массивами. Вектор столбцы и вектор строки 1. Урок 7Скачать

Дистанционные курсы
для педагогов
548 курсов от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
«Учителя года» проведут открытые занятия для педагогов России
Время чтения: 1 минута
Регионы запустили работу по капремонту школ
Время чтения: 1 минута
Свободное движение повышает креативность
Время чтения: 1 минута
В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей
Время чтения: 1 минута
В России утвердили новые правила аккредитации образовательных учреждений
Время чтения: 1 минута
В Петербурге дали рекомендации по переводу школьников на дистант
Время чтения: 3 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy урокиСкачать

Вес вектора столбца значений функции
Определение. Говорят, что булева функция f(x1, …, xi, …, xn) существенно зависит от переменной xi, если выполняется условие
В этом случае также говорят, что переменная xi существенная, в противном случае ее называют фиктивной переменной.
Пример. Рассмотрим булеву функцию f(x1, x2, x3) и исследуем ее переменные x1 и x3.
Из таблиц истинности видно, что переменная x1 функции f(x1, x2, x3) существенная, так как f(0,x2, x3) ≠ f(1,x2, x3). Переменная x3 фиктивная, так как f(x1, x2, 0) = f(x1, x2, 1). •
Очевидно, что для выявления фиктивных переменных можно не строить в явном виде таблиц истинности левой и правой частей неравенства, а сравнивать соответствующие части вектора-столбца значений функции.
Алгоритм распознавания фиктивной переменной по таблице истинности.
– Для переменной x1 сравниваются половины столбца значений функции: верхняя и нижняя, так как именно в верхней половине x1=0, а в нижней x1=1, если они совпадают, то переменная x1 фиктивна;
– для переменной x2 сравниваются четвертины столбца в каждой половине, так как именно в верхних четвертинах x2 =0, а в нижних x2 =1, если четвертины в каждой половине совпадают, то переменная x2 фиктивна;
– и так далее (за четвертинами следуют 1/8, 1/16, … ).
Пример. Для булевой функции из предыдущего примера переменная x1 существенна, так как верхняя половина столбца значений функции (0011) не равна нижней половине (1100). Переменная x2 существенна, так как четвертины уже в первой половине различаются (00 и 11). Переменная x3 фиктивна, так как осьмушки во всех четвертинах равны (0 и 0, 1 и 1, 1 и 1, 0 и 0). •
Выявление фиктивных переменных можно ускорить, используя следующее очевидное утверждение.
Достаточное условие отсутствия фиктивных переменных. Если вес вектора-столбца значений функции нечетен, то функция не может содержать фиктивных переменных.
Алгоритм удаления фиктивной переменной xi состоит в вычеркивании из таблицы истинности всех строк, в которых xi = 0 (или всех строк, в которых xi = 1), и столбца xi.
Пример (функция та же). Применив алгоритм для удаления фиктивной переменой x3 (таблица слева), получаем результат (таблица справа).
Если переменная xi функции f(x1, …, xn) фиктивна, то на наборах, соседних по i компоненте, функция принимает одинаковые значения. Отсюда следует способ выявления и удаления фиктивной переменной функции, заданной матрицей Грея.
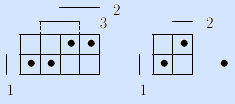
Алгоритм распознавания фиктивной переменной по матрице Грея (основан на свойстве симметрии кода Грея).
Переменная фиктивна тогда и только тогда, когда точки на матрице расположены симметрично относительно осей этой переменной. Упрощенная матрица – это одна из ее симметричных половин.
Пример (функция та же и представлена на левой матрице). Переменная x3 функции фиктивна. Справа показан результат ее удаления.
Определение. Булевы функции назовем равными с точностью до фиктивных переменных, если равны (в смысле, определенном ранее) функции, полученные из исходных удалением фиктивных переменных (и именно это расширенное толкование равенства функций мы будем иметь в виду во всех дальнейших рассуждениях).
Пример. Рассмотрим функции f1(x1, x2) и f2(x1, x2). Удалив фиктивную переменную x1 функции f1(x1, x2) и фиктивную переменную x2 функции f2(x1, x2), получим равные функции f1(x2)=f2(x1)=f(x). Значит, исходные функции равны с точностью до фиктивных переменных.
Видео:Квантовая механика 8 - Операторы. Собственные векторы и собственные значения.Скачать

Как определить фиктивную переменную
Определение. Говорят, что булева функция f(x1, …, xi, …, xn) существенно зависит от переменной xi, если выполняется условие
В этом случае также говорят, что переменная xi существенная, в противном случае ее называют фиктивной переменной.
Пример. Рассмотрим булеву функцию f(x1, x2, x3) и исследуем ее переменные x1 и x3.
Из таблиц истинности видно, что переменная x1 функции f(x1, x2, x3) существенная, так как f(0,x2, x3) ≠ f(1,x2, x3). Переменная x3 фиктивная, так как f(x1, x2, 0) = f(x1, x2, 1). •
Очевидно, что для выявления фиктивных переменных можно не строить в явном виде таблиц истинности левой и правой частей неравенства, а сравнивать соответствующие части вектора-столбца значений функции.
Алгоритм распознавания фиктивной переменной по таблице истинности.
– Для переменной x1 сравниваются половины столбца значений функции: верхняя и нижняя, так как именно в верхней половине x1=0, а в нижней x1=1, если они совпадают, то переменная x1 фиктивна;
– для переменной x2 сравниваются четвертины столбца в каждой половине, так как именно в верхних четвертинах x2 =0, а в нижних x2 =1, если четвертины в каждой половине совпадают, то переменная x2 фиктивна;
– и так далее (за четвертинами следуют 1/8, 1/16, … ).
Пример. Для булевой функции из предыдущего примера переменная x1 существенна, так как верхняя половина столбца значений функции (0011) не равна нижней половине (1100). Переменная x2 существенна, так как четвертины уже в первой половине различаются (00 и 11). Переменная x3 фиктивна, так как осьмушки во всех четвертинах равны (0 и 0, 1 и 1, 1 и 1, 0 и 0). •
Выявление фиктивных переменных можно ускорить, используя следующее очевидное утверждение.
Достаточное условие отсутствия фиктивных переменных. Если вес вектора-столбца значений функции нечетен, то функция не может содержать фиктивных переменных.
Алгоритм удаления фиктивной переменной xi состоит в вычеркивании из таблицы истинности всех строк, в которых xi = 0 (или всех строк, в которых xi = 1), и столбца xi.
Пример (функция та же). Применив алгоритм для удаления фиктивной переменой x3 (таблица слева), получаем результат (таблица справа).
Если переменная xi функции f(x1, …, xn) фиктивна, то на наборах, соседних по i компоненте, функция принимает одинаковые значения. Отсюда следует способ выявления и удаления фиктивной переменной функции, заданной матрицей Грея.
Алгоритм распознавания фиктивной переменной по матрице Грея (основан на свойстве симметрии кода Грея).
Переменная фиктивна тогда и только тогда, когда точки на матрице расположены симметрично относительно осей этой переменной. Упрощенная матрица – это одна из ее симметричных половин.
Пример (функция та же и представлена на левой матрице). Переменная x3 функции фиктивна. Справа показан результат ее удаления.
Определение. Булевы функции назовем равными с точностью до фиктивных переменных, если равны (в смысле, определенном ранее) функции, полученные из исходных удалением фиктивных переменных (и именно это расширенное толкование равенства функций мы будем иметь в виду во всех дальнейших рассуждениях).
Пример. Рассмотрим функции f1(x1, x2) и f2(x1, x2). Удалив фиктивную переменную x1 функции f1(x1, x2) и фиктивную переменную x2 функции f2(x1, x2), получим равные функции f1(x2)=f2(x1)=f(x). Значит, исходные функции равны с точностью до фиктивных переменных.
В вышеприведённых таблицах выделена графа «фиктивные переменные», т.е. переменные, от которых функция на самом деле не зависит. Остановимся на этом понятии подробнее.
Пример: Рассмотрим булевы функции f(x,y) = xÚy и g(x,y,z) = (xÙy)Ú(хÙ 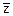
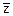
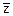
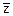
В этом примере функция, в которой присутствуют 3 переменных, в действительности зависит от 2-х. В дискретной математике, по сравнению с непрерывной, понятие фиктивных переменных играет большую роль.
Определение: Переменная х является существенной переменной для функции f(x, x1,…, xn-1), если существует хотя бы один набор (x1,…, xn-1) такой, что f(0, x1,…, xn-1) ≠ f(1, x1,…, xn-1)
В противном случае переменная называется фиктивной, или несущественной. Понятно, что в определении переменную можно ставить на любое место, и фиктивных переменных может быть несколько.
Ключевым понятием в теории булевых функций является понятие равенства функций. Для функций от одного и того же числа переменных нет необходимости рассматривать какое-то специальное определение равенства, ибо такие функции равны, если они совпадают как отображения одного о того же булева куба. Существование фиктивных переменных усложняет ситуацию, и проблема состоит в том, чтобы определить равенство булевых функций в целом, независимо от числа переменных.
Булевы функции f и g равны, если их существенные переменные совпадают и на каждом наборе значений этих переменных функции f и g принимают равные значения.
Кроме процедуры удаления фиктивных переменных используют и процедуру добавления к множеству переменных булевой функции одной или нескольких переменных.
В результате понятие фиктивной переменной позволяет любые две функции рассматривать как функции от одних и тех же переменных. Для этого надо рассмотреть объединение множеств переменных XUY и дополнить множества X и Y до объединения, вводя соответствующие переменные как фиктивные.
Нетрудно распространить описанную конструкцию на произвольное конечное множество функций и считать тем самым все функции этого множества функциями от одного и того же числа переменных.
Введём понятие проектирующей функции.
Функцию pri от n переменных, такую, что
называют (i-ой) проектирующей функцией. В общем случае нумерация множества переменных может быть не задана, и следует указывать не номер, а саму переменную.
Из определения следует, что проектирующая функция имеет единственную существенную переменную, а все остальные переменные проектирующей функции являются фиктивными. Далее мы всегда будем обозначать проектирующую функцию её символом – х, имея в виду возможность расширения на любое число переменных. Такое обозначение есть, конечно вольность, т.к. функция как бы отождествляется с аргументом. Отождествление функции и аргумента недопустимо, т.к. понятие переменной, хоть и связано с понятием функции, никак не есть частный случай понятия функции. Переменная – это имя, некий символ, но никак не функция. Тем не менее мы будем использовать это обозначение ради краткости.
Не нашли то, что искали? Воспользуйтесь поиском:
Видео:Как разложить вектор по базису - bezbotvyСкачать

Вход в систему
Видео:Машинное обучение. Метод опорных векторов. К.В. Воронцов, Школа анализа данных, Яндекс.Скачать

Навигация
Видео:Дискретная математика. ДНФСкачать

Последние комментарии
- ПСЗ
5 недель 4 дня назад - Наверное вот так вот ?
6 недель 5 дней назад - Спасибо
6 недель 5 дней назад - Эльдар
7 недель 4 дня назад - Умножение двух положительных чисел в Ассемблере МиК
7 недель 4 дня назад - Да
8 недель 16 часов назад - А вот почему, ВЛАД, .
8 недель 1 день назад - Почему? Я когда писал код,
8 недель 1 день назад - Продолжу.
8 недель 1 день назад - Снова Влад
8 недель 1 день назад
Видео:Математика это не ИсламСкачать

О существенных и фиктивных переменных булевых функций
Воспроизведём данное на лекции определение существенности переменной БФ.
Определение. Пусть задана некоторая БФ f(x1, x2, …,xk, …,xn).
Переменная xk этой функции называется существенной, если найдётся набор ДВОИЧНЫХ значений такой, что:
Рассмотрим пример. Пусть БФ f( x1, x2, x3) задана таблицей:
f( x1, x2, x3)
Исследуем переменные этой функции на существенность.
- x1– существенна, т.к., например, при f(x1, 0, 1), имеем f(0, 0, 1)=0, f(1, 0, 1)=1. Т.е. f(0, 0, 1) f(1, 0, 1). Здесь нашлись двоичные значения = такие, что f(0,a2,a3) f(1,a2,a3).
- x2– не существенна, т.к. f(a1, 0,a3) = f(a1, 1,a3)на любых наборах двоичных значениий (проверьте это по таблице!).
- x3– существенна, т.к., например, при f(0, 0,x3), имеем f(0, 0, 0)=1, f(0, 0, 1)=0. Т.е. f(0, 0, 0) f(0, 0, 1). Здесь нашлись двоичные значения = такие, что f(a1,a2, 0) f(a1,a2, 1).
Если в таблично заданной функции f( x1, x2, …,xk, …,xn), например, переменная xk – не существенна, то для исключения её из таблицы и, соответственно, уменьшения арности указанной функции, необходимо:
- вычеркнуть из таблицы столбец несущественной переменной xk;
- вычеркнуть из таблицы все строки, в пересечении которых с вычеркнутым столбцом стоят нули.
Так как x2 в выше приведённом примере – не существенна (фиктивна), то действуя так, как описано выше, её из таблицы можно исключить.
В результате получим таблицу:
f(x1, x3)
При желании, в полученной таблице, переменные, для удобства, можно переименовать, например, в x1, x2, или в x, y. На функцию, как на отображение, такие переименования никакого влияния не окажут.
Ясно, что выполняя описанные операции в обратном порядке, фиктивные переменные можно в таблицу включать, формально увеличивая, тем самым, арность задаваемой этой таблицей БФ.
Определение . Две булевы функции f1 и f2 будем называть равными (эквивалентными), если таблицу f2 можно получить из таблицы f1 путём добавления и/или изъятия фиктивных переменных, а также, возможно, переименования (любых) переменных.
В дальнейшем, БФ рассматриваются с точностью до их равенства (т.е. равные функции нами различаться не будут).
Если функции f1 и f2 равны, то этот факт будем обозначать как f1 = f2.
Замечание. Возможность добавления фиктивных переменных позволяет считать что БФ, образующие любое рассматриваемое конечное множество всегда имеют одну и ту же арность.
Критерий фиктивности переменной БФ.
Пусть БФ f(x1, x2, …,xk, …,xn) определена таблично. Для выявления фиктивности её переменной xk, удобно использовать следующий критерий:
- Вычислим величину L=2 n- k+1 ;
- Разобьём столбец значений функции (он последний в таблице) на равные отрезки длины L;
- Если в каждом из полученных на шаге 2 отрезке верхняя половина отрезка совпадает с нижней его половиной, то проверяемая переменная xk – фиктивна, иначе, она не фиктивна, т.е. существенна.
Задание. Убедитесь в том, что приведённый критерий работает, применив его к переменным x1, x2, x3 рассмотренного выше примера табличного задания БФ f( x1, x2, x3).
📸 Видео
РЕАЛИЗАЦИЯ ЛИНЕЙНОЙ РЕГРЕССИИ | Линейная регрессия | LinearRegression | МАШИННОЕ ОБУЧЕНИЕСкачать
Квантовая механика 7 - Вектор состояния. Амплитуда вероятности.Скачать

Собственные векторы и собственные числа линейного оператораСкачать

A.7.17 Барицентрические координаты? Это просто!Скачать

Булевы функцииСкачать

19-1 Булевы функции. ПримерыСкачать

Вышмат. Теорема о неявном отображении: практический, аналитический и геометрические смыслыСкачать

LQR и фильтр Калмана | Утро с теорией управления, лекция 10Скачать

Булевы функции и способы их заданияСкачать

Урок 28 (осн). Вычисление массы и объема тела по плотностиСкачать

Машграф 2013 4 лекцияСкачать