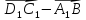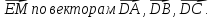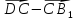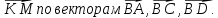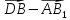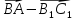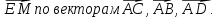В данной публикации мы рассмотрим, какие векторы называются коллинеарными и перечислим условия, при которых они являются таковыми. Также разберем примеры решения задач по этой теме.
- Условия коллинеарности векторов
- Примеры задач
- Коллинеарность векторов, условия коллинеарности векторов.
- Условия коллинеарности векторов
- Примеры задач на коллинеарность векторов
- Примеры задач на коллинеарность векторов на плоскости
- Примеры задач на коллинеарность векторов в пространстве
- Зачёт по теме «Векторы в пространстве»
- Просмотр содержимого документа «Зачёт по теме «Векторы в пространстве»»
- 🎥 Видео
Видео:Коллинеарные векторы.Скачать

Условия коллинеарности векторов
Векторы, лежащие на одной или нескольких параллельных прямых, называются коллинеарными.
Два вектора коллинеарны, если выполняется одно из условий ниже:
1. Существует такое число n, при котором .
2. Отношения координат векторов равны. Но данное условие не может применяться, если одна из координат равняется нулю.
3. Векторное произведение равно нулевому вектору (применимо только для трехмерных задач).
Видео:Коллинеарность векторовСкачать

Примеры задач
Задание 1
Даны векторы , и . Определим, есть ли среди них коллинеарные.
Решение:
У заданных векторов нет нулевых координат, значит мы можем применить второе условие коллинеарности.
Следовательно, коллинеарными являются только векторы a и c .
Задание 2
Выясним, при каком значении n векторы и коллинеарны.
Решение:
Т.к. среди координат нет нулей, согласно второму условию мы можем составить их соотношение, чтобы рассчитать недостающий элемент.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Коллинеарность векторов, условия коллинеарности векторов.
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 1).
 |
| рис. 1 |
Видео:10 класс, 43 урок, Компланарные векторыСкачать

Условия коллинеарности векторов
Два вектора будут коллинеарны при выполнении любого из этих условий:
Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что
N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.
N.B. Условие 3 применимо только для трехмерных (пространственных) задач.
Доказательство третего условия коллинеарности
Пусть есть два коллинеарные вектора a = < ax ; ay ; az > и b = < nax ; nay ; naz >. Найдем их векторное произведение
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Примеры задач на коллинеарность векторов
Примеры задач на коллинеарность векторов на плоскости
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:
| ax | = | ay | . |
| bx | by |
| Вектора a и b коллинеарны т.к. | 1 | = | 2 | . |
| 4 | 8 |
| Вектора a и с не коллинеарны т.к. | 1 | ≠ | 2 | . |
| 5 | 9 |
| Вектора с и b не коллинеарны т.к. | 5 | ≠ | 9 | . |
| 4 | 8 |
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
Для этого найдем ненулевой компонент вектора a в данном случае это ay . Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение n a :
Так как b = n a , то вектора a и b коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | . |
| bx | by |
| 3 | = | 2 | . |
| 9 | n |
Решим это уравнение:
| n = | 2 · 9 | = 6 |
| 3 |
Ответ: вектора a и b коллинеарны при n = 6.
Примеры задач на коллинеарность векторов в пространстве
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:
| ax | = | ay | = | az | . |
| bx | by | bz |
Вектора a и b коллинеарны т.к. 1 4 = 2 8 = 3 12
Вектора a и с не коллинеарны т.к. 1 5 = 2 10 ≠ 3 12
Вектора с и b не коллинеарны т.к. 5 4 = 10 8 ≠ 12 12
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
Для этого найдем ненулевой компонент вектора a в данном случае это ay . Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение n a :
Так как b = n a , то вектора a и b коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | = | az | . |
| bx | by | bz |
| 3 | = | 2 | = | m |
| 9 | n | 12 |
Из этого соотношения получим два уравнения:
| 3 | = | 2 |
| 9 | n |
| 3 | = | m |
| 9 | 12 |
Решим эти уравнения:
| n = | 2 · 9 | = 6 |
| 3 |
| m = | 3 · 12 | = 4 |
| 9 |
Ответ: вектора a и b коллинеарны при n = 6 и m = 4.
Видео:Вектор. Определение. Коллинеарные векторы. Равные векторы.Скачать

Зачёт по теме «Векторы в пространстве»
Зачёт по теме «Векторы в пространстве» (4 варианта).
Просмотр содержимого документа
«Зачёт по теме «Векторы в пространстве»»
Зачёт по теме «Векторы в пространстве»
Верно ли, что векторы, лежащие на боковых рёбрах призмы , коллинеарны?
Могут ли три компланарных вектора лежать на трёх взаимно перпендикулярных прямых?
Дан параллелепипед АВСDA1B 1C1D1 . Изобразите на рисунке векторы, равные: а) 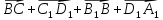
В тетраэдре DABC точка Е – середина DB, а М – точка пересечения медиан грани АВС. Разложите вектор
Зачёт по теме «Векторы в пространстве»
Верно ли, что векторы, лежащие на боковых рёбрах пирамиды, коллинеарны?
Могут ли три некомпланарных вектора лежать на трёх параллельных прямых?
Дан параллелепипед АВСDA1B 1C1D1 . Изобразите на рисунке векторы, равные: а) 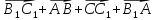
В тетраэдре DABC М – точка пересечения медиан грани ACD, а K – середина АВ. Разложите вектор
Зачёт по теме «Векторы в пространстве»
Верно ли, что векторы, лежащие на двух прямых, перпендикулярных к третьей , коллинеарны?
Могут ли три вектора, один из которых является суммой двух других, быть некомпланарными?
Дан параллелепипед АВСDA1B 1C1D1 . Изобразите на рисунке векторы, равные: а) 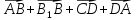
В тетраэдре DABC точка Е – середина DB, а М – точка пересечения медиан грани АВС. Разложите вектор
Зачёт по теме «Векторы в пространстве»
Верно ли, что векторы, лежащие в двух параллельных плоскостях, коллинеарны?
Могут ли три вектора, один из которых является разностью двух других, быть некомпланарными?
Дан параллелепипед АВСDA1B 1C1D1 . Изобразите на рисунке векторы, равные: а) 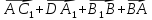
В тетраэдре DABC М – точка пересечения медиан грани BDC, а E – середина АC. Разложите вектор
🎥 Видео
Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

№913. Векторы a и b коллинеарны. Коллинеарны ли векторы: а) а +3b и а; б) b-2а и a? Ответ обоснуйте.Скачать

Угол между векторами. 9 класс.Скачать

ГЕОМЕТРИЯ 11 класс: Компланарные векторыСкачать

Понятие вектора. Коллинеарные векторы.Скачать
Задача 2. Коллинеарны ли векторы с1 и с2, построенные по векторам a и b?Скачать

§15 Коллинеарность векторовСкачать
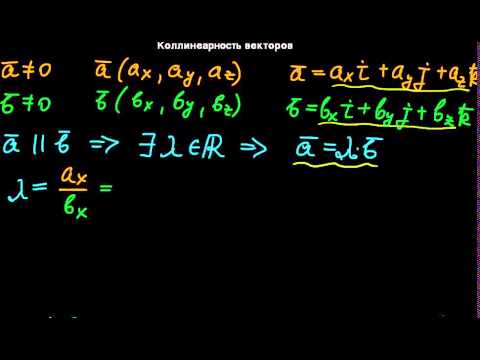
9 класс, 1 урок, Разложение вектора по двум неколлинеарным векторамСкачать

Разложение вектора на неколлинеарные вектора.Скачать

Геометрия 10 класс (Урок№18 - Компланарные векторы. Векторный метод решения задач.)Скачать

Что такое вектор? | Коллинеарные векторы | Сонаправленные векторы | МегаШколаСкачать

Задача 1. Коллинеарность векторов. Высшая математика.Скачать

Геометрия. 10 класс. Коллинеарность и компланарность векторов /13.04.2021/Скачать