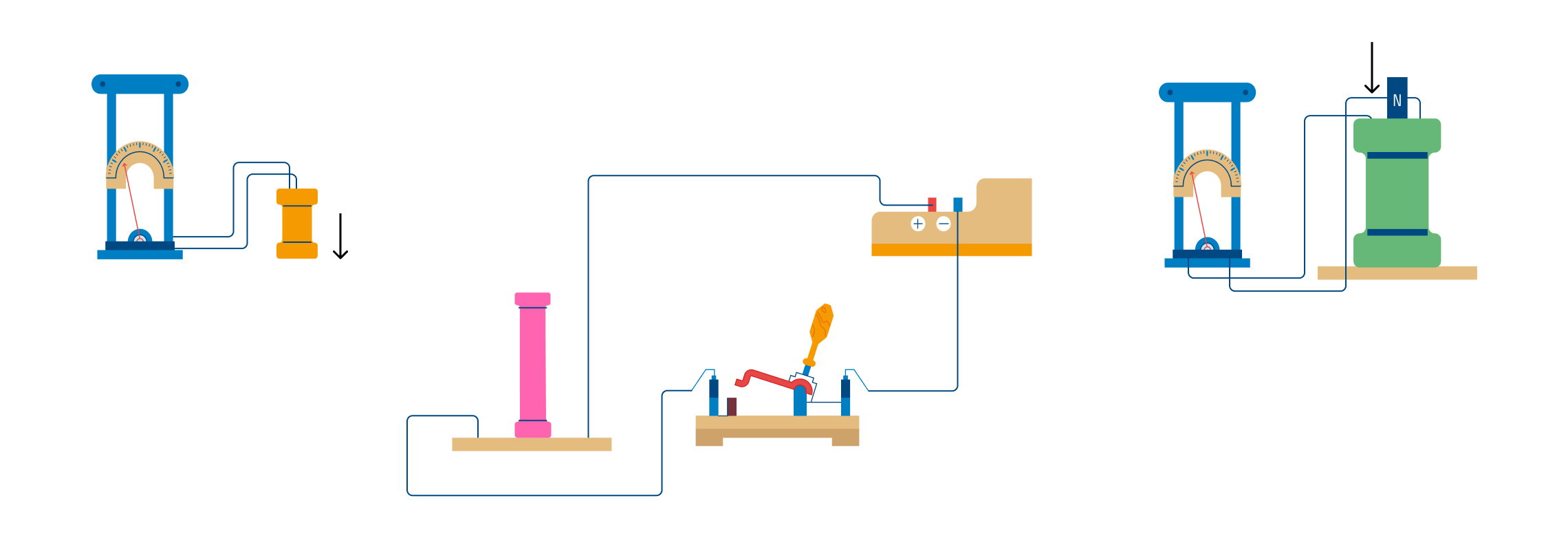
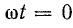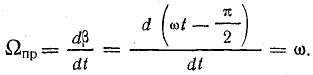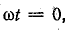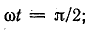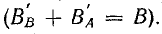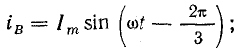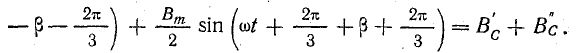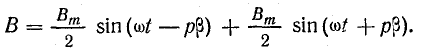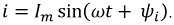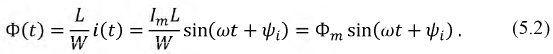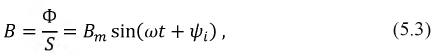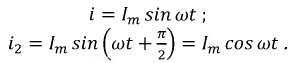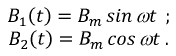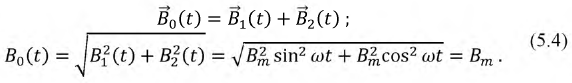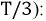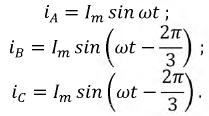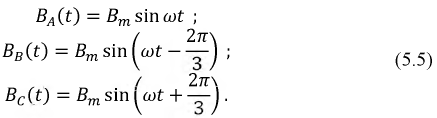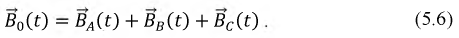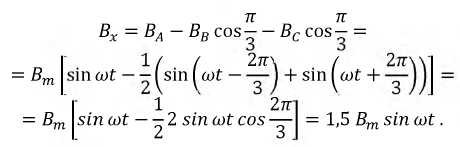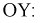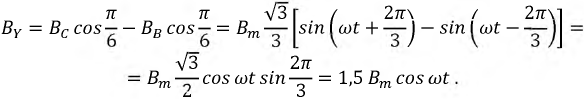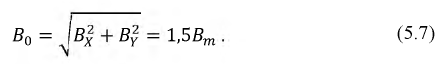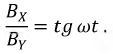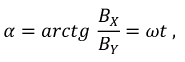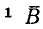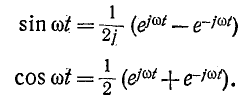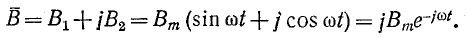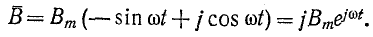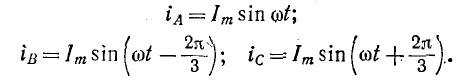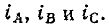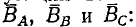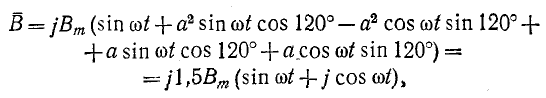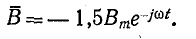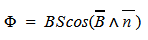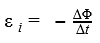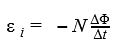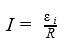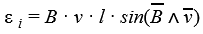Рассмотрим проводник (рис. 99) длиной /, движущийся в однородном магнитном поле со
скоростью v (вектор магнитной индукции В перпендикулярен проводнику и составляете направлением скорости v проводника угол а).
На свободные заряды проводника, движущиеся вместе с проводником, действует сила Лоренца [см. (55.2)1
На пути / работа силы Лоренца, действующей на заряд Q.
ЭДС индукции в отрезке проводника определяется работой силы Лоренца по перемещению единичного положительного заряда вдоль проводника, т. е., согласно (70.1),
Формула (70.2) определяет ЭДС индукции для любого проводника длиной /, движущегося со скоростью v в однородном магнитном поле.
Согласно закону Фарадея, возникновение ЭДС электромагнитной индукции возможно и в случае неподвижного контура, находящегося в переменном магнитном поле. Однако сила Лоренца на неподвижные заряды не действует, поэтому в данном случае ею нельзя объяснить возникновение ЭДС индукции.
Максвелл для объяснения ЭДС индукции в неподвижных проводниках предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле ?„, которое и является причиной возникновения индукционного тока в проводнике. Циркуляция Ев |см. (7.4)| по любому неподвижному контуру L проводника представляет собой ЭДС электромагнитной индукции:
- Вращение рамки в магнитном поле
- Вращающееся магнитное поле
- Получение вращающегося магнитного поля
- Системы обмоток для получения магнитного поля
- Графики магнитной индукции магнитного поля
- Принцип действия синхронного и асинхронного электродвигателей
- Пульсирующее магнитное поле
- Магнитное поле однофазной обмотки при постоянном токе
- Пульсирующее магнитное поле
- Разложение пульсирующего магнитного поля на два вращающихся поля
- Уравнения вращающегося магнитного поля
- Вращающееся магнитное поле двухфазной обмотки
- Вращающееся магнитное поле трехфазной обмотки
- Зависимость частоты вращения магнитного поля от числа пар полюсов
- Способы получения вращающегося магнитного поля
- Вращающееся магнитное поле системы двух катушек
- Вращающееся магнитное поле системы трёх катушек
- Вращающееся магнитное поле
- Закон электромагнитной индукции
- Магнитный поток
- Электромагнитная индукция
- Закон электромагнитной индукции
- Правило Ленца
- 📹 Видео
Видео:Правило рук 👋 КАК ЛЕГКО определять НАПРАВЛЕНИЕ ЛИНИЙ МАГНИТНОГО ПОЛЯ??Скачать

Вращение рамки в магнитном поле
Вращение плоской рамки в однородном магнитном поле раскрывает принцип действия генераторов, применяемых для преобразования механической энергии в энергию электрического тока.
Пусть рамка вращается в однородном магнитном поле (В = const) равномерно с угловой скоростью w = const (рис. 100). Магнитный поток, сцепленный с рамкой площадью S, в любой момент времени I, согласно (60.1), равен
где а = о/ — угол поворота рамки в момент времени t (начало отсчета выбрано так, чтобы при t = 0 было а = 0).
При вращении рамки в ней будет возникать переменная ЭДС индукции |см. (69.2)):
изменяющаяся со временем по гармоническому закону. ЭДС %. максимальна при sin со/ = 1, т. е.
Учитывая (71.2), выражение (71.1) можно записать в виде
Таким образом, если в однородном магнитном поле равномерно вращается рамка, то в ней возникает переменная ЭДС, изменяющаяся по гармоническому закону.
Из формулы (71.2) вытекает, что ??тх (следовательно, и ЭДС индукции) находится в прямой зависимости от величин ш, В и S. В России принята стандартная частота тока v = = 50 Гц, поэто-
му возможно лишь возрастание двух остальных величин. Для увеличения В применяют мощные постоянные магниты или в электромагнитах пропускают значительный ток, а также внутрь электромагнита помещают сердечники из материалов с большой магнитной проницаемостью р. Если вращать не один, а ряд витков, соединенных последовательно, то тем самым увеличивается S. Переменное напряжение снимается с вращающегося витка с помощью щеток, схематически изображенных на рис. 100.
Процесс превращения механической энергии в электрическую обратим. Если по рамке, помешенной в магнитное поле, пропускать ток, то на нее будет действовать вращающий момент и рамка начнет вращаться. На этом принципе основана работа электродвигателей, предназначенных для превращения электрической энергии в механическую.
Видео:Рамка с током в магнитном поле. 8 класс.Скачать

Вращающееся магнитное поле
Содержание:
Вращающееся магнитное поле:
Было отмечено, что развитие трехфазных систем связано с широким применением электродвигателей переменного тока.
Принципы работы электрических машин переменного тока основаны на использовании вращающихся магнитных полей, которые получаются с помощью многофазных (чаще всего трехфазных) систем.
Относительно простая возможность получения вращающегося магнитного поля является одним из основных достоинств многофазной системы.
Видео:Поток вектора магнитной индукцииСкачать

Получение вращающегося магнитного поля
Общее понятие о вращающемся магнитном поле можно получить, рассматривая рис. 12.3.
При неподвижном роторе генератора переменного тока магнитная индукция в воздушном зазоре под полюсом постоянна во времени, так как в обмотке возбуждения имеется постоянный ток. Однако в пространстве вдоль воздушного зазора магнитная индукция распределена по синусоидальному закону [см. формулу (12.3) и график рис. 12.2, б]. Когда ротор вращается с постоянной скоростью, магнитное поле во вращающемся полюсе по-прежнему постоянно во времени и неподвижно относительно полюса, но в каждой точке воздушного зазора магнитная индукция изменяется во времени также по синусоидальному закону.
При этом наибольшей величины Bm магнитная индукция достигает последовательно в каждой точке воздушного зазора, когда эта точка оказывается против середины полюса.
Относительно неподвижного статора магнитное поле вращается вместе с полюсами.
Системы обмоток для получения магнитного поля
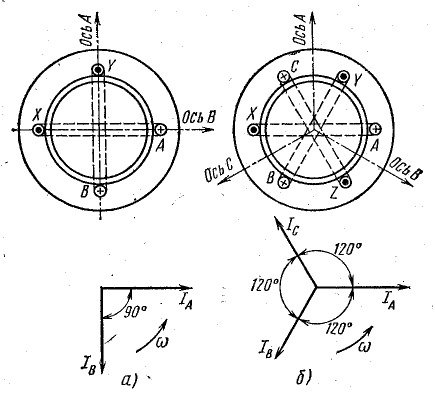
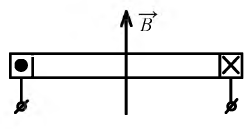
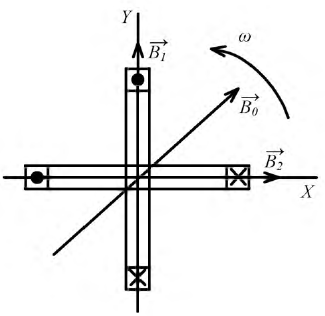
Вращающееся магнитное поле можно получить также с помощью неподвижной системы обмоток, если в них имеются синусоидальные токи, не совпадающие по фазе. На рис. 22.1 схематично показаны две такие системы простейших обмоток: двухфазная (а) и трехфазная (б), имеющие по одной катушке на фазу. Оси катушек двухфазной системы взаимно перпендикулярны, оси катушек трехфазной системы пересекаются под углом 120° друг к другу. Синусоидальные токи в катушках имеют одинаковые амплитуды и частоту, но по фазе сдвинуты относительно друг друга в первом случае на 90°, а во втором— на 120°.
Стороны катушек, где начала витков, обозначены А, В, С. Противоположные стороны, где концы витков X, Y, Z, отстоят от соответствующих начал по окружности статора на 180°.
Условно-положительное направление токов в обмотках отмечено крестиками в начале витков и точками в конце. Этим условно-положительным направлениям токов по правилу буравчика соответствуют условно-положительные направления осей магнитных потоков, совпадающих с осями одноименных катушек.
Рис. 22.1. Системы обмоток для получения вращающегося магнитного поля
Магнитное поле такой системы обмоток с токами образуется наложением полей отдельных фаз.
Графики магнитной индукции магнитного поля
Наглядное представление о вращении магнитного поля дает рис. 22.2, где определено направление оси полюсов в различные моменты времени и показаны графики магнитной индукции в воздушном зазоре поля каждой фазы и результирующего поля.
При
В соответствии со знаками токов отмечены их направления в проводниках в рассматриваемый момент времени.
Вся система проводников по направлению тока делится на две части: в одной из них направление тока отмечено крестиком, а в другой — точкой.
По правилу буравчика определены направления магнитных потоков каждой катушки в отдельности и результирующего потока.
Результирующее магнитное поле условно изображено двумя линиями магнитной индукции (штриховые линии).
По направлению этих линий определяется положение полюсов. Слева от нейтрали находятся северный полюс ротора и южный полюс статора (линии магнитной индукции выходят из поверхности ротора в воздушный зазор и входят в поверхность статора). Справа от нейтрали находятся южный полюс ротора и северный полюс статора.
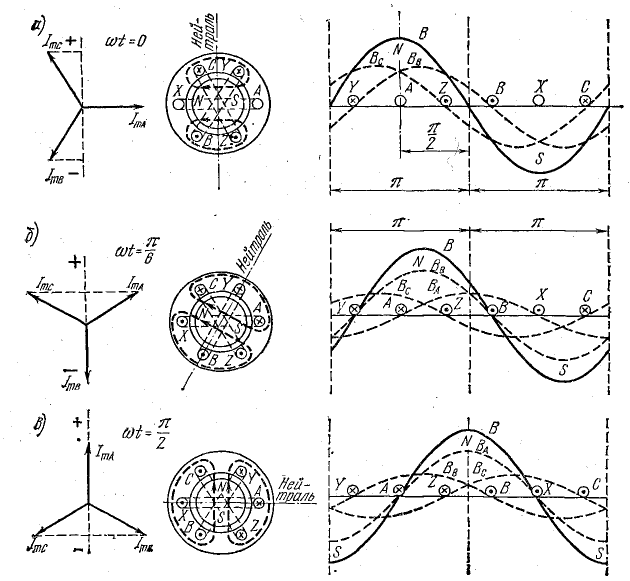
Рис. 22.2. Векторные диаграммы токов и графики магнитной индукции вращающегося магнитного поля
Для момента времени, соответствующего фазовому углу 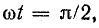
Нетрудно заметить, что за время, соответствующее фазовому углу π/2, ось полюсов в пространстве повернулась, т. е. северный и южный магнитные полюса переместились относительно неподвижных обмоток на такой же угол π/2.
Проведя аналогичные рассуждения для последующих моментов времени, например соответствующих фазовым углам 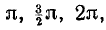
Изменение токов в фазах происходит не скачком, а плавно, по синусоидальному закону (векторы токов вращаются равномерно с угловой скоростью ω), поэтому и магнитное поле меняет свое направление не скачком, а равномерно, поворачиваясь при данной системе обмоток за один период тока на один оборот.
Подтверждением этому служит рис. 22.2, б, где определено направление оси полюсов при 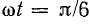
Интересно отметить, что в тот момент, когда ток в одной из фаз достигает наибольшей величины, ось полюсов результирующего магнитного поля совпадает с осью полюсов поля этой фазы (на рис. 22.2, в результирующее поле направлено так же, как поле фазы А, при этом ток в фазе А максимальный: 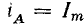
На основании этого легко определить направление вращения магнитного поля.
При прямой последовательности токов в фазах максимумы их наступают в порядке 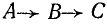
Если на статоре обмотки фаз расположены так, что обход их в указанном порядке совершается в направлении движения часовой стрелки, то и поле вращается в ту же сторону.
При обратной последовательности токов в фазах 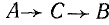
Принцип действия синхронного и асинхронного электродвигателей
С помощью вращающегося магнитного поля электрическая энергия преобразуется в механическую. Для этой цели служат электрические трехфазные двигатели — синхронные и асинхронные, из которых наиболее распространены последние.
Поместим во вращающееся магнитное поле замкнутый виток в виде прямоугольной рамки (рис. 22.3, а).
При вращении поля проводники рамки пересекаются линиями магнитной индукции, в силу чего в них наводится э. д. с. Направление э. д. с. определено по правилу правой руки и отмечено на рисунке крестиком и точкой.
Применяя правило правой руки, нужно учитывать относительное движение проводников рамки против вращающегося поля. Под действием э. д .с. в рамке образуется ток такого же направления. Но проводники с током в магнитном поле испытывают действие электромагнитных сил, направленных в соответствии с правилом левой руки. Относительно оси рамки электромагнитные силы образуют момент, под действием которого рамка вращается в сторону вращения поля.
Частота вращения рамки всегда меньше скорости поля: 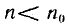
Скольжение оценивается величиной в процентах: 
Вращение рамки с частотой поля невозможно, так как при 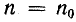
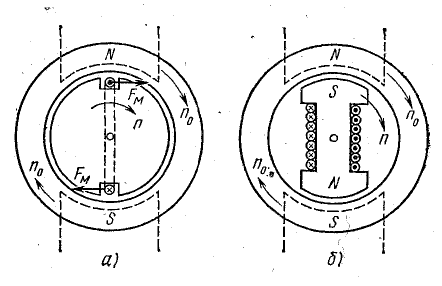
Рис. 22.3. К вопросу о принципах работы электродвигателей переменного тока
Электрические двигатели, работающие по этому принципу, называют асинхронными.
Если вместо короткозамкнутой рамки в магнитном поле поместить постоянный магнит или электромагнит с постоянным током в его обмотке, то благодаря взаимодействию вращающегося поля с полем постоянного магнита образуется вращающий момент, также направленный в сторону вращения поля (рис. 22.3, б).
Постоянный магнит в постоянном магнитном поле стремится занять положение, при котором ось полюсов магнита в направлении от южного полюса к северному совпадает с направлением внешнего поля. Постоянный магнит «увлекается» за вращающимся полем, т. е. вращается в ту же сторону и с той же частотой, что и поле: 
Электрические двигатели, работающие по такому принципу, называют синхронными.
Видео:Опыты по физике. Вращение рамки с током в магнитном полеСкачать

Пульсирующее магнитное поле
Вращающееся магнитное поле образуется системой обмоток, сдвинутых в пространстве.
Для более полного представления об особенностях вращающегося магнитного поля рассмотрим магнитное поле одной фазы электрической машины.
Магнитное поле однофазной обмотки при постоянном токе
Одна фаза трехфазной обмотки схематично показана на рис. 22.4, а, причем проводники ее распределены равномерно на 1/3 внутренней поверхности статора (распределенные обмотки наиболее распространены). Две другие фазы отдельно занимают такие же участки поверхности статора, так что в целом трехфазная обмотка представляет собой систему проводников, равномерно распределенных вдоль воздушного зазора.
Плоскость, перпендикулярная оси магнитного потока, которой статор и ротор делятся на две части, называют нейтралью. На одной из них находится северный полюс, а на другой — южный (на рис. 22.4 обозначены полюса ротора).
Целесообразно также рассмотреть развертку статора, т. е. представить цилиндрическую поверхность статора разрезанной в одном месте по образующей и развернутой на плоскости (рис. 22.4, б).
Проведем вокруг части проводников катушки замкнутый контур 1-2-3-4 и напишем для него уравнение по закону полного тока 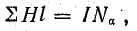
где 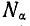
Магнитным сопротивлением стальной части магнитопровода можно пренебречь, так как 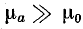
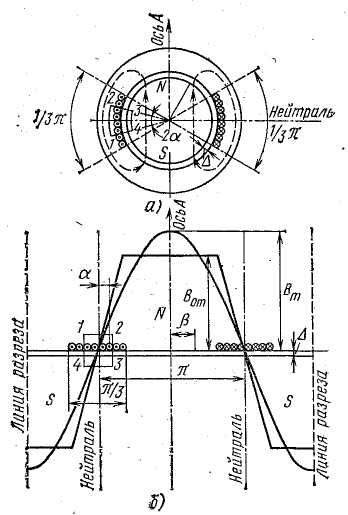
Рис. 22.4. Распределение магнитной индукции в воздушном зазоре генератора
При равномерном расположении проводников 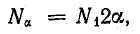
где N1 — число проводников, приходящееся на единицу центрального угла окружности статора: 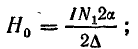
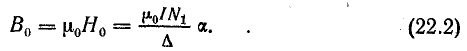
Из формулы (22.2) видно, что магнитная индукция в воздушном зазоре той части окружности статора, где располагаются проводники обмотки, изменяется пропорционально расстоянию от нейтрали, т.е. вдоль воздушного зазора, по прямолинейному закону.
При 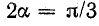
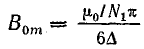
Эта величина магнитной индукции в воздушном зазоре сохраняется на всем протяжении окружности статора, где нет проводников. Таким образом, однофазная обмотка образует одну пару магнитных полюсов (N и S), а график распределения магнитной индукции представляет собой равнобокую трапецию.
По форме такой график близок к синусоиде, поэтому для упрощения последующих выводов заменим действительный график синусоидальной кривой с амплитудой Вm, уравнение которой запишем относительно начала координат, расположенного на оси полюсов (ось А): 
где β — угол по окружности статора, отсчитанный от оси А в положительном направлении (по часовой стрелке).
Замена трапециевидной кривой синусоидой в данном случае означает, что учитывается только составляющая основной частоты, а остальные составляющие в целях упрощения не учитываются.
Пульсирующее магнитное поле
При постоянном токе такое распределение магнитной индукции вдоль воздушного зазора сохраняется, пока имеется ток в катушке.
При переменном токе в катушке 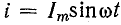
Магнитное поле в этом случае «пульсирует», поэтому оно и называется пульсирующим. В воздушном зазоре образуется стоячая волна магнитной индукции.
На рис. 22.5 показано распределение магнитной индукции в различные моменты времени (кривые 1, 2 и т. д.).
Уравнение магнитной индукции пульсирующего поля легко получить, подставив в уравнение (22.3) выражение переменного тока: 
где Вm — магнитная индукция на оси А при токе в обмотке 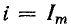
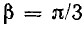
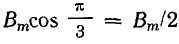
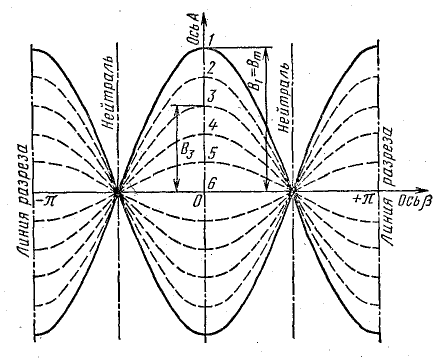
Рис. 22.5. Графики магнитной индукции пульсирующего магнитного поля
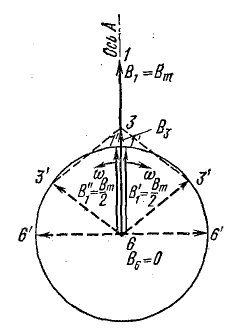
Рис. 22.6. Векторная диаграмма пульсирующего магнитного поля
При 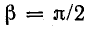
Разложение пульсирующего магнитного поля на два вращающихся поля
Из тригонометрии известно, что 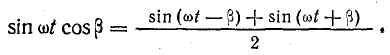
Применив эту формулу, уравнение (22.4) можно написать в виде 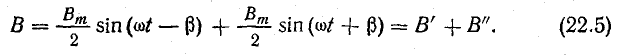
Отсюда видно, что пульсирующее магнитное поле можно представить в виде двух составляющих, каждая из которых является функцией двух переменных t и β. Первая составляющая В’ имеет наибольшую величину при 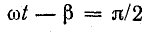
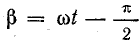
Наибольшая величина магнитной индукции не меняется, если одновременно изменяются 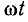
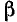
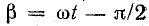
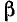
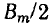
Эта составляющая пульсирующего поля представляет собой прямую волну магнитной индукции поля, вращающегося по часовой стрелке.
Составляющая В» представляет собой обратную волну магнитной индукции, так как она перемещается в обратном направлении против движения часовой стрелки.
При 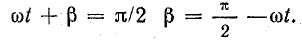
Угловая скорость обратной волны 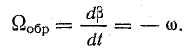
Такое изменение обеих составляющих магнитной индукции в каждой точке вдоль воздушного зазора можно представить синусоидальными графиками, перемещающимися по окружности статора с угловой скоростью 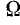
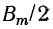
1 — при токе в катушке 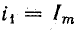
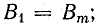
3 — при токе в катушке 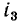
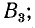
6 — при токе в катушке 
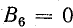
Этими же номерами отмечены графики магнитной индукции пульсирующего поля на рис. 22.5.
Если длина вращающегося вектора магнитной индукции не меняется (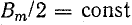
Таким образом, пульсирующее магнитное поле можно разложить на два круговых, вращающихся в противоположные стороны с одинаковой частотой.
Задача 22.4.
Разложить в векторной форме пульсирующее поле каждой фазы трехфазной обмотки на два вращающихся и найти вектор магнитной индукции результирующего поля для моментов времени, соответствующих фазовым углам: 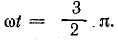
Решение. Для фазового угла 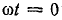
Когда ток в фазе достигает наибольшей величины Im, магнитная индукция пульсирующего поля этой фазы становится равной Вm (магнитная индукция принимается пропорциональной току). Вращающиеся составляющие пульсирующего поля имеют наибольшую величину магнитной индукции 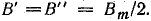
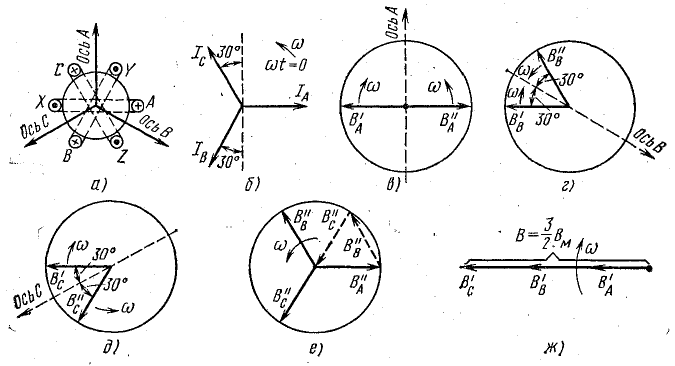
Рис. 22.7. К задаче 22.4
Симметричная система векторов токов для момента времени 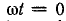
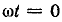
Ток в фазе С опережает ток в фазе А на 120°. С того момента, когда ток в фазе С имел наибольшее положительное значение, вектор тока повернулся на 30°.
В соответствии с этим на рис. 22.7, д векторы вращающихся составляющих поля фазы С нанесены под углом 30° к положительному направлению оси полюсов фазы С, пройдя это направление.
Составляющие магнитной индукции поля каждой фазы, вращающиеся против движения часовой стрелки, сдвинуты относительно друг друга на 120°, т. е. образуют симметричную систему векторов, сумма которых равна нулю (рис. 22.7, е). .
Составляющие магнитной индукции поля каждой фазы, вращающиеся по часовой стрелке, направлены в одну сторону и складываются арифметически (рис. 22.7, ж): 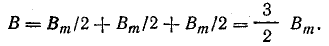
Выполните аналогичные построения для двух других заданных значений 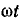
Уравнения вращающегося магнитного поля
Особенности вращающегося магнитного поля выясняются наиболее полно при помощи аналитических выражений, которые нетрудно получить на базе предыдущих рассуждений.
Вращающееся магнитное поле двухфазной обмотки
Уравнение магнитной индукции поля двухфазной обмотки можно получить, представив магнитную индукцию пульсирующего поля каждой фазы вращающимися составляющими. Учитывая пространственный сдвиг катушек обмотки на 90° и временной сдвиг токов в фазах на такой же угол, запишем при токах в фазах 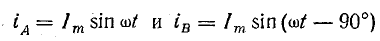
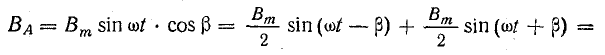
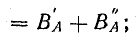
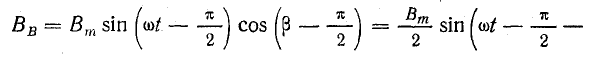
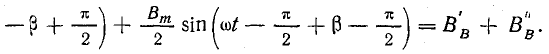
Сумма составляющих, вращающихся против положительного направления отсчета углов, равна нулю: 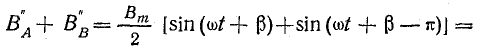
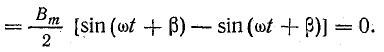
Сумма составляющих магнитной индукции полей, вращающихся в прямом направлении, равна индукции результирующего поля двухфазной обмотки: 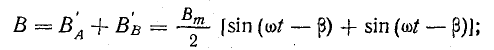

Из уравнения (22.6) видно, что двухфазная система обмоток рис. 22.8, а, имеющая пространственный сдвиг фаз на 90° при временном сдвиге токов в них на такой же угол, создает вращающееся круговое магнитное поле.
На рис. 22.8 эти выводы подтверждаются векторными диаграммами.
Ток в фазе А iA = 0 при 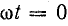
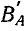
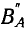
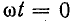
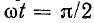
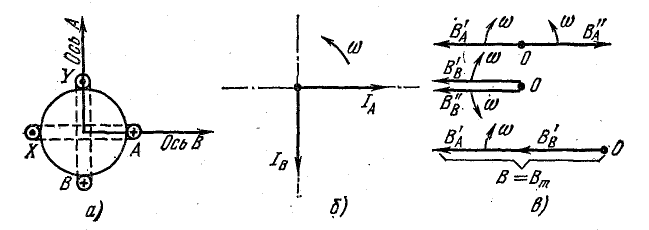
Рис. 22.8. Векторные диаграммы вращающегося магнитного поля двухфазной обмотки
Ток в фазе В при 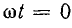
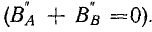
Вращающееся магнитное поле трехфазной обмотки
Предположим, что токи в фазах трехфазной обмотки (см. рис. 22.1, б) изменяются согласно уравнениям
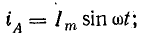
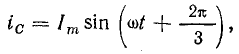
т. е. составляют симметричную систему токов.
Пульсирующее магнитное поле каждой фазы выразим его вращающимися составляющими, учитывая временной сдвиг токов в фазах и пространственный сдвиг осей магнитных потоков на 120°: 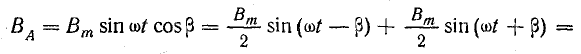
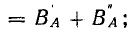
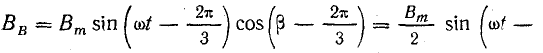
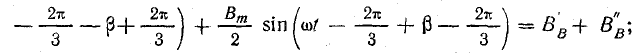
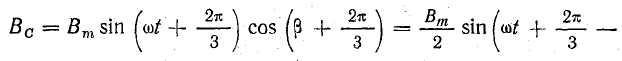
Магнитная индукция результирующего поля в любой точке воздушного зазора равна алгебраической сумме магнитных индукций от каждой обмотки, так как линии магнитной индукции выходят из стали в воздух под углом 90° к границе раздела сред: 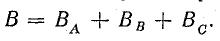
Сумма составляющих магнитной индукции 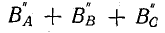
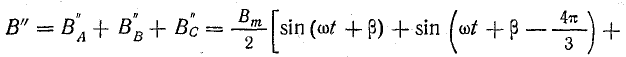
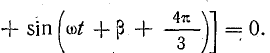
Магнитная индукция результирующего поля трехфазной обмотки равна сумме составляющих, вращающихся в положительном направлении (по часовой стрелке). Все эти составляющие равны друг другу: 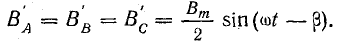
Поэтому 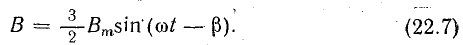
Наибольшая величина магнитной индукции поля трехфазной обмотки (см. рис. 22.1, б), равная 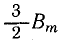
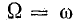
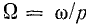
Зависимость частоты вращения магнитного поля от числа пар полюсов
Обмотку каждой фазы можно выполнить из двух частей с шагом 90°, как показано на рис. 22.9, или из трех частей и более, располагая каждую из них соответственно на 1/2 или 1/3 окружности и т. д. Все рассуждения, ранее отнесенные к одной паре полюсов на полной окружности, остаются справедливыми и здесь, с той лишь разницей, что их нужно отнести теперь к одной паре полюсов на 1/2, 1/3 окружности и т. д. Число пар полюсов на полной окружности будет 2, 3 или в общем случае р. Вдоль воздушного зазора магнитная индукция достигает наибольшей положительной величины р раз, поэтому уравнение ее нужно записать так: 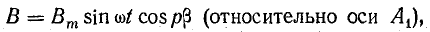
или
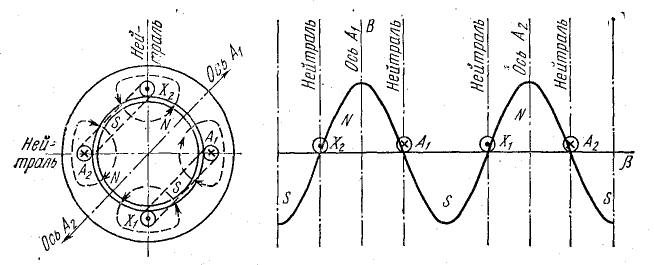
Рис. 22.9. Схема одной фазы четырехполюсной обмотки. График магнитной индукции
Угловая скорость 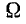
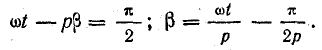
Отсюда 
Частота вращения магнитного поля обратно пропорциональна числу пар полюсов, образуемых обмоткой с током.
Задача 22.5.
Построить кривую вращающегося магнитного поля, т. е. начертить геометрическое место концов вектора результирующей магнитной индукции поля двух катушек, сдвинутых в пространстве на угол 90°, в которых токи сдвинуты по фазе на угол π/2, а отношение амплитуд 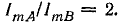
Магнитную индукцию считать пропорциональной току.
Решение. Оси магнитных потоков обеих катушек сохраняют неизменным свое направление в пространстве, так как катушки неподвижны (рис. 22.10, а). Поле каждой катушки пульсирующее; следовательно, вектор магнитной индукции направлен все время по одной прямой. Нанесем на чертеже две взаимно перпендикулярные прямые, представляющие собой оси пульсирующих магнитных потоков первой и второй катушек (рис. 22.10, в).
Изменение векторов магнитной индукции обеих катушек можно проследить на временной векторной диаграмме (рис. 22.10, б).
Оба вектора 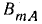
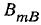
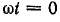
Оставляя неподвижными векторы, будем поворачивать ось времени по часовой стрелке.
Векторы индукции поля каждой катушки будем откладывать по осям магнитных потоков на рис. 22.10, в.
Магнитную индукцию результирующего поля находим векторным сложением ее составляющих: В, ВA, ВB.
Построение показывает, что конец вектора магнитной индукции результирующего поля описывает эллипс. Такое поле называется эллиптическим.
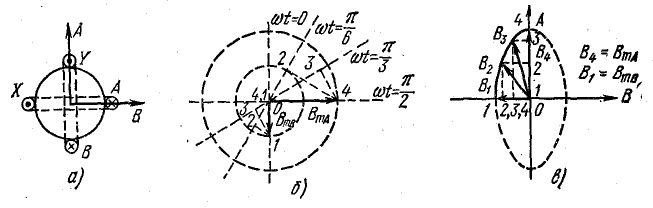
Рис. 22.10. К задаче 22.5
Видео:Урок 178 (осн). Рамка с током в магнитном поле. ЭлектродвигательСкачать

Способы получения вращающегося магнитного поля
Пульсирующее магнитное поле:
Вращающееся магнитное поле нашло исключительно широкое практическое применение. С его помощью реализован принцип работы большинства электрических машин (асинхронные и синхронные двигатели, образующие класс трёхфазных машин, а также двухфазные двигатели переменного тока). Рассмотрение этого вопроса начнем с понятия пульсирующего поля. Пусть по катушке, изображенной на рис. 5.1, протекает синусоидальный ток
Рис. 5.1. Условное представление катушки индуктивности
Соответственно, магнитная индукция будет:
где 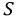
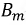
Ток и магнитный поток изменяются в фазе. Поскольку ток синусоидален, то синусоидальными являются магнитный поток и магнитная индукция, т.е. магнитный поток меняется как по величине, так и по направлению (см. рис. 5.1) — это и есть пульсирующее магнитное поле.
Вращающееся магнитное поле системы двух катушек
Пусть даны две одинаковые катушки, оси которых расположены в пространстве под углом 90° по отношению друг к другу (рис. 5.2).
Рис. 5.2. Система двух катушек с пространственным сдвигом на 90°
Пусть токи катушек изменяются по законам:
Временной и пространственный сдвиг катушек составляет 90°. При этом в каждой из них возникает свое пульсирующее магнитное поле, т.е.:
Полученный результат показывает, что результирующая магнитная индукция не зависит от времени и равна амплитуде магнитной индукции одной из катушек.
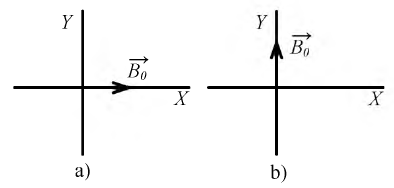
Оценим значения 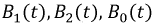
при 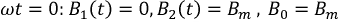
при 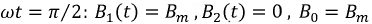
Очевидно, что вектор 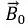
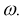
Рис. 5.3. Положение вектора магнитной индукции в разные моменты времени
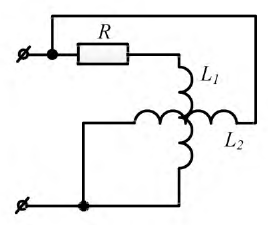
Таким образом, для получения вращающегося магнитного поля необходимо, чтобы одна катушка обладала большой индуктивностью, но имела малое активное сопротивление, а вторая — наоборот (рис. 5.4). При этом достигается фазовый сдвиг примерно на 90°.
Рис. 5.4. Способ получения пространственного и фазового сдвига магнитных полей на угол 90°.
Вращающееся магнитное поле системы трёх катушек
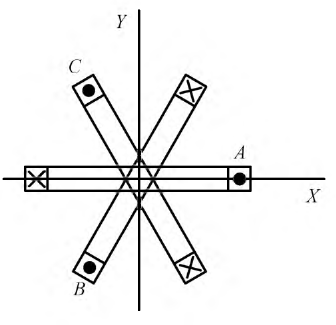
Рассмотрим систему трёх катушек, оси которых сдвинуты на угол 120° (рис. 5.5).
Рис. 5.5. Система трёх катушек с пространственным сдвигом на угол 120°
Катушки жестко закреплены, кроме того, токи имеют временной сдвиг на 120° (на
Соответствующие им магнитные индукции будут:
В каждый из этих катушек существует пульсирующее магнитное поле. Найдём суммарное магнитное поле этих катушек:
Определим вначале проекции векторов на каждую из осей (рис. 5.6) декартовой системы координат.
Рис. 5.6. Векторы 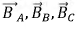
Ось
Ось
В итоге получим:
Полученный результат показывает, что амплитуда магнитной индукции не меняется во времени, но в отличие от системы двух катушек в полтора раза больше амплитуды магнитной индукции любой из катушек. Это, в свою очередь, говорит о том, что работа, совершаемая полем трёх катушек, будет в полтора раза больше, чем работа, совершаемая полем двух катушек.
Найдем отношения проекций 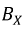
Пусть 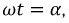
то есть вектор результирующей магнитной индукции 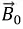
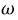
Вращающееся магнитное поле
Пусть через катушку проходит ток 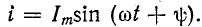
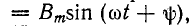
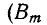
Таким образом, магнитное поле изменяется (пульсирует) вдоль оси катушки; такое магнитное поле называется пульсирующим.
Условимся круговым вращающимся магнитным полем называть магнитное поле, ось которого равномерно вращается, причем значение магнитной индукции на
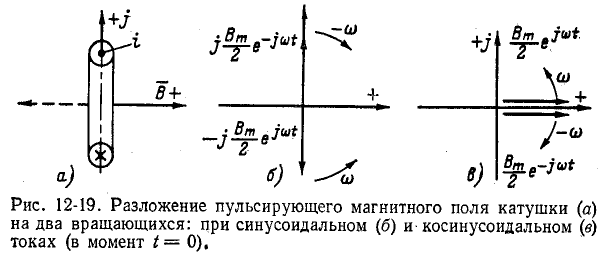
этой оси неизменно. Легко убедиться в том, что магнитное поле, пульсирующее по закону синуса или косинуса, может рассматриваться как результат наложения двух круговых полей, вращающихся в противоположные стороны с угловой скоростью, равной угловой частоте переменного тока, и имеющих максимальную индукцию на вращающейся оси, вдвое меньшую амплитуды индукции пульсирующего поля (рис. 12-19, б и б). Это следует из формул
Положения векторов на рис. 12-19, б и б соответствуют моменту t = 0.
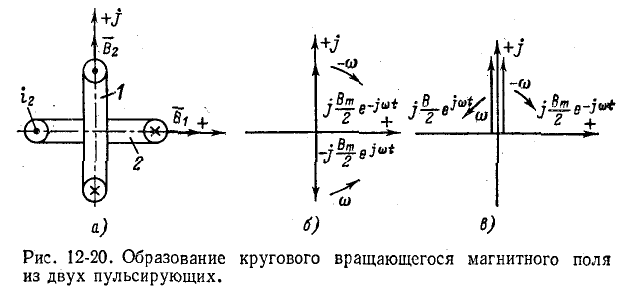
той же амплитуды и частоты, сдвинутые по фазе друг относительно друга па четверть периода. На рис. 12-20, а катушки обозначены цифрами 1 и 2. Принятым положительным направлениям токов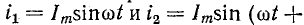
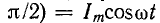
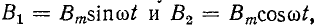
Заменив каждое из пульсирующих полей двумя вращающимися (рис. 12-20, б и в), убеждаемся в том, что
векторы магнитной индукции 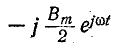
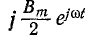
направлении, взаимно компенсируются (их сумма равна нулю). Два других вектора образуют в сумме вектор магнитной индукции 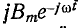
К тому же выводу приходим и на основании выражения, получаемого для результирующего вектора магнитной индукции,
Это выражение показывает, что ось результирующего магнитного поля равномерно вращается с угловой скоростью 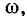
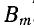
Направление вращения магнитного поля зависит от положительных направлений магнитных индукций и от того, какая из индукций является отстающей. В рассматриваемом здесь случае индукция 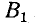
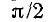
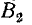
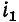
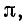
Таким образом, от сложения двух взаимно перпендикулярных пульсирующих магнитных полей, сдвинутых по фазе на четверть периода, получается круговое магнитное поле, вращающееся с угловой скоростью в сторону отстающего по фазе вектора индукции.
Описанный способ получения кругового вращающегося магнитного поля с помощью двухфазной системы токов широко используется в приборо-и электромашиностроении.
Большое удобство с точки зрения возможности получения кругового вращающегося поля представляет трехфазный ток.
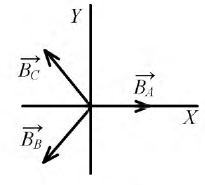
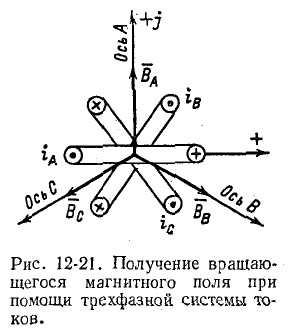
Расположим три одинаковые катушки таким образом, чтобы их оси были сдвинуты друг относительно друга в пространстве на угол 120° (рис. 12-21), и подключим эти катушки к симметричной трехфазной цепи. Тогда через катушки будут протекать токи:
Положительным направлениям токов, обозначенным на рис. 12-21 с помощью точек и крестиков, соответствуют по правилу буравчика указанные стрелками положительные направления магнитных потоков (векторов индукций), создаваемых токами
При пропорциональной зависимости индукций от токов мгновенные значения индукций фаз выразятся следующим образом:
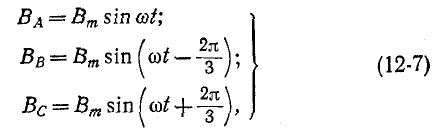
где 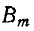
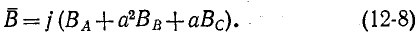
Подстановка (12-7) в (12-8) дает:
Полученное выражение показывает, что результирующий вектор магнитного поля имеет постоянный модуль, равный 1,5 Вт, и равномерно вращается с угловой скоростью а от оси фазы А по направлению к оси фазы В и т. д. (на рис. 12-21 — по ходу часовой стрелки), т. е. получается круговое вращающееся поле.
Для изменения направления вращения поля достаточно поменять местами токи в каких-нибудь двух катушках, например
При несимметрии токов в катушках, например если концы одной катушки поменять местами, или при несимметрии питающих напряжений вместо кругового вращающегося поля получится эллиптическое вращающееся поле, результирующий вектор индукции которого описывает эллипс и имеет переменную угловую скорость.
В электрических машинах вращающееся магнитное поле осуществляется с помощью обмоток, размещаемых в пазах неподвижной части машины — статора.
Линии магнитной индукции замыкаются по телу статора, воздушному зазору и телу ротора. Место выхода линий индукции из статора можно рассматривать как северный полюс, а место входа их в статор — как южный полюс магнитного поля обмотки статора.
Кривая распределения индукции В вдоль воздушного зазора имеет ступенчатую форму, которая при большом числе пазов статора близка к трапеции с углом наклона боковой стороны 60°, и может быть приближенно заменена синусоидой.
Синусоидальный ток частоты f, проходя через фазную обмотку статора, создает поле, пульсирующее с той же частотой. Таким образом, магнитное поле одной фазы изменяется синусоидально как во времени, так и в пространстве (по окружности зазора).
Обмотки трех фаз расположены на статоре так, что их оси, а следовательно, и оси трех пульсирующих магнитных полей сдвинуты в пространстве на 120°. Поэтому при прохождении через обмотку трехфазного тока пульсирующие поля образуют в сумме двухполюсное вращающееся в зазоре синусоидальное поле, амплитуда индукции которого постоянна и равна 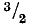
За один период переменного тока такое магнитное поле совершит один оборот, а за 1 мин 60f оборотов.
Если обмотку статора выполнить многополюсной, т. е. с полюсным шагом 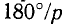
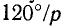
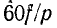
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Электрические цепи синусоидального тока
- Электрические цепи несинусоидального тока
- Несинусоидальный ток
- Электрические цепи с распределенными параметрами
- Цепи периодического несинусоидального тока
- Резонанс токов
- Трехфазные симметричные цепи
- Трехфазные несимметричные цепи
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Урок 281. Электромагнитная индукция. Магнитный поток. Правило ЛенцаСкачать

Закон электромагнитной индукции
О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Вращение рамки в магнитном поле.Скачать

Магнитный поток
Прежде, чем разобраться с тем, что такое электромагнитная индукция, нужно определить такую сущность, как магнитный поток.
Представьте, что вы взяли обруч в руки и вышли на улицу в ливень. Чем сильнее ливень, тем больше через этот обруч пройдет воды — поток воды больше.
Если обруч расположен горизонтально, то через него пройдет много воды. А если начать его поворачивать — уже меньше, потому что он расположен не под прямым углом к вертикали.
Теперь давайте поставим обруч вертикально — ни одной капли не пройдет сквозь него (если ветер не подует, конечно).
Магнитный поток по сути своей — это тот же самый поток воды через обруч, только считаем мы величину прошедшего через площадь магнитного поля, а не дождя.
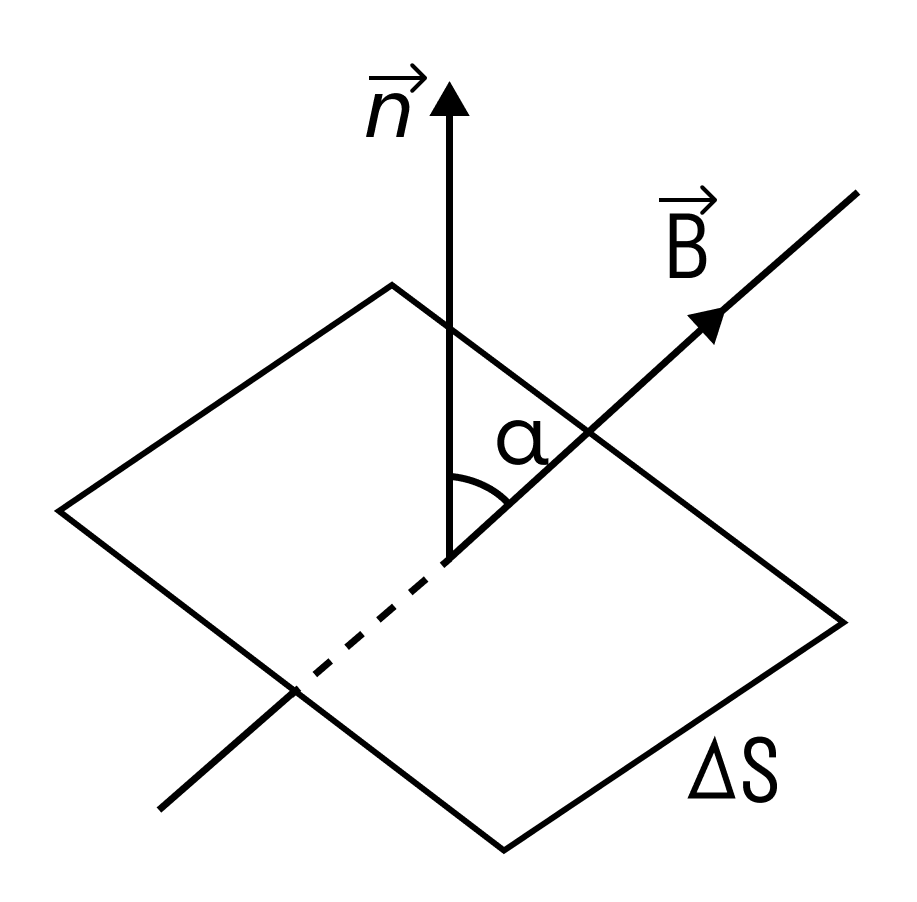
Магнитным потоком через площадь S контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции B, площади поверхности S, пронизываемой данным потоком, и косинуса угла α между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):