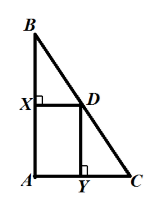Треугольник по 4 точкам

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На данном уроке мы рассмотрим четыре замечательные точки треугольника. На двух из них остановимся подробно, вспомним доказательства важных теорем и решим задачу. Остальные две вспомним и охарактеризуем.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Основы геометрии»

Видео:Уравнения стороны треугольника и медианыСкачать

Четыре замечательные точки треугольника

Вы будете перенаправлены на Автор24

В треугольнике есть так называемые четыре замечательные точки: точка пересечения медиан. Точка пересечения биссектрис, точка пересечения высот и точка пересечения серединных перпендикуляров. Рассмотрим каждую из них.

Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Точка пересечения медиан треугольника

О пересечении медиан треуголника: Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении $2:1$ начиная с вершины.

Доказательство.

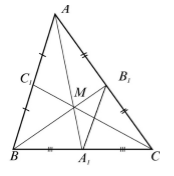
Рассмотрим треугольник $ABC$, где $_1, _1, _1$ его медианы. Так как медианы делят стороны пополам. Рассмотрим среднюю линию $A_1B_1$ (Рис. 1).

Рисунок 1. Медианы треугольника

По теореме 1, $AB||A_1B_1$ и $AB=2A_1B_1$, следовательно, $angle ABB_1=angle BB_1A_1, angle BAA_1=angle AA_1B_1$. Значит треугольники $ABM$ и $A_1B_1M$ подобны по первому признаку подобия треугольников. Тогда

Аналогично доказывается, что

Видео:Урок по теме ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ ТРЕУГОЛЬНИКА ГЕОМЕТРИЯ 8 КЛАСССкачать

Точка пересечения биссектрис треугольника

О пересечении биссектрис треугольника: Биссектрисы треугольника пересекаются в одной точке.

Доказательство.

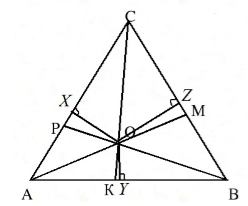
Рассмотрим треугольник $ABC$, где $AM, BP, CK$ его биссектрисы. Пусть точка $O$ — точка пересечения биссектрис $AM и BP$. Проведем из этой точки перпендикуляры к сторонам треугольника (рис. 2).

Рисунок 2. Биссектрисы треугольника

Готовые работы на аналогичную тему

Для доказательства нам потребуется следующая теорема.

Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.

По теореме 3, имеем: $OX=OZ, OX=OY$. Следовательно, $OY=OZ$. Значит точка $O$ равноудалена от сторон угла $ACB$ и, значит, лежит на его биссектрисе $CK$.

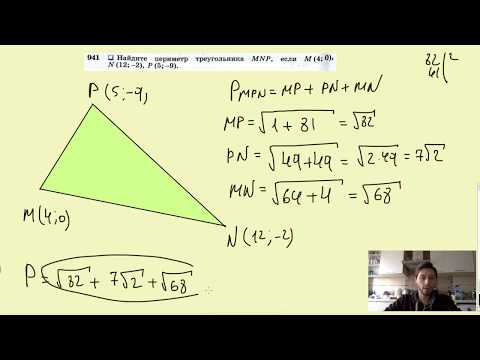
Видео:№941. Найдите периметр треугольника MNP, если М (4; 0), N(12; -2), В (5; -9).Скачать

Точка пересечения серединных перпендикуляров треугольника

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство.

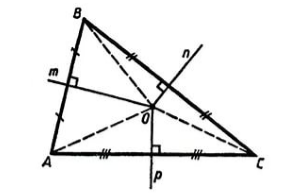
Пусть дан треугольник $ABC$, $n, m, p$ его серединные перпендикуляры. Пусть точка $O$ — точка пересечения серединных перпендикуляров $n и m$ (рис. 3).

Рисунок 3. Серединные перпендикуляры треугольника

Для доказательства нам потребуется следующая теорема.

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов данного отрезка.

По теореме 3, имеем: $OB=OC, OB=OA$. Следовательно, $OA=OC$. Значит точка $O$ равноудалена от концов отрезка $AC$ и, значит, лежит на его серединном перпендикуляре $p$.

Видео:Как строить сечения тетраэдра и пирамидыСкачать

Точка пересечения высот треугольника

Высоты треугольника или их продолжения пересекаются в одной точке.

Доказательство.

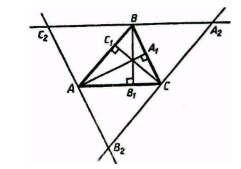
Рассмотрим треугольник $ABC$, где $_1, _1, _1$ его высоты. Проведем через каждую вершину треугольника прямую, параллельную противоположной вершине стороне. Получаем новый треугольник $A_2B_2C_2$ (рис. 4).

Рисунок 4. Высоты треугольника

Так как $AC_2BC$ и $B_2ABC$ параллелограммы с общей стороной, то $AC_2=AB_2$, то есть точка $A$ — середина стороны $C_2B_2$. Аналогично, получаем, что точка $B$ — середина стороны $C_2A_2$, а точка $C$ — середина стороны $A_2B_2$. Из построения мы имеем, что $_1bot A_2B_2, _1bot A_2C_2, _1bot C_2B_2$. Следовательно, $_1, _1, _1$ — серединные перпендикуляры треугольника $A_2B_2C_2$. Тогда, по теореме 4, имеем, что высоты $_1, _1, _1$ пересекаются в одной точке.

Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Пример задачи на использование 4 замечательных точек треугольника

Серединные перпендикуляры к сторонам $AB$ и $AC$ треугольника $ABC$ пересекаются в точке $D$ стороны $BC$. Докажите, что

а) точка $D$ — середина стороны $BC$.

б) $angle A=angle B+angle C$

Решение.

а) По теореме 4, все серединные перпендикуляры пересекаются в точке $D$. Следовательно, $D$ — основание серединного перпендикуляра к стороне $BC$. Значит точка $D$ — середина стороны $BC$.

б) Так как $X$ и $D$ — середины сторон, то $XD$ — средняя линия треугольника. Тогда, по теореме о средней линии треугольника $XD||AC$. Значит,$angle A=angle DXB$, как соответственные углы. Значит, $angle A=^0$. Тогда$angle B+angle C=^0-angle A=^0-^0=^0=angle A$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 29 03 2021

Видео:Замечательные точки треуг-ка. 8 класс.Скачать

Тема: «четыре замечательные точки треугольника»

ТЕМА: «ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ ТРЕУГОЛЬНИКА»

Свойства биссектрисы угла

Все точки биссектрисы угла равноудалены от сторон этого угла.

Свойства серединного перпендикуляра к отрезку

Все точки серединного перпендикуляра к отрезку равноудалены от концов этого отрезка.

Четыре замечательные точки треугольника

1) Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2 : 1, считая от вершины;

2) Биссектрисы треугольника пересекаются в одной точке;

3) Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке;

4) Высоты треугольника (или их продолжения) пересекаются в одной точке.

Найдите соответствующие точки, построив указанные элементы треугольника:

1) 2)

3) 4)

Пример 1. По данным рисунка найдите площадь треугольника BOQ, если QM = 9, BT = 12.

1) QM, BT – медианы ⇒ QO : OM = BO : OT = 2 : 1 (по свойству медиан треугольника);

2) QO : OM = 2 : 1, QM = 9 ⇒ QO = 2OM, QM = 3OM ⇒

OM = 9 : 3 = 3, QO = 9 – 3 = 6;

3) BO : OT = 2 : 1, BT = 12 ⇒ BO = 2OT, BT = 3OT ⇒

OT = 12 : 3 = 4, BO = 12 – 4 = 8;

4) QM⊥BT ⇒ ΔBOQ – прямоугольный ⇒ SBOQ = (по формуле площади прямоугольного треугольника).

Пример 2. По данным рисунка найдите угол FNO, если угол MKN = 66°.

1) Продолжим NO до пересечения со стороной КМ. КМ∩NO = Р;

2) О – точка пересечения высот ⇒ NP – высота ΔKMN ⇒ NP⊥КМ ⇒ ΔKPM – прямоугольный;

3) ΔKPM – прямоугольный ⇒ ∠РKN + ∠КNР = 90° (по свойству острых углов прямоугольного треугольника);

∠КNР = 90° — ∠РKN = 90° — 66° = 24°;

Пример 3. По данным рисунка найдите ОК, если RO = 20.

OM, ON – серед. перп.;

1) О – точка пересечения серединных перпендикуляров ⇒ ОК – серединный перпендикуляр (по свойству серединных перпендикуляров треугольника);

2) ОМ – серединный перпендикуляр ⇒ RO = PO = 20 (свойство серединного перпендикуляра к отрезку);

3) ОК – серединный перпендикуляр ⇒ ΔРОК – прямоугольный ⇒ ОК = (по свойству катета прямоугольного треугольника, лежащего против угла 30°).

Пример 4. По данным рисунка найти угол МСВ1?

1) Продлим СМ до пересечения с АВ, АВ∩СС1 = С1,

М – точка пересечения биссектрис треугольника ⇒ СС1 – биссектриса треугольника АВС (по свойству биссектрис треугольника);

2) Рассмотрим ΔАВМ: ∠АМВ + ∠ВАМ + ∠АВМ = 180° ⇒ ∠ВАМ + ∠АВМ = 180° — 128° = 52°;

3) ВВ1, АА1 – биссектрисы ΔАВС ⇒ ∠А = 2∠ВАМ, ∠В = 2∠АВМ;

4) По теореме о сумме углов треугольника: ∠С = 180° — (∠А + ∠В) = 180° — (2∠ВАМ + 2∠АВМ) = 180° — 2(∠ВАМ + ∠АВМ) = 180° — 2 ⋅ 52° = 76°;

5) СС1 – биссектриса ∠С ⇒ ∠МСВ1 = ∠С : 2 = 38°.

💥 Видео

Математика без Ху!ни. Уравнение плоскости.Скачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Корнеев С.А. - Комбинаторика и сложность вычислений - 13. Вычисление биномиальных коэффициентовСкачать

Вычисляем высоту через координаты вершин 1Скачать

Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

ГЕОМЕТРИЯ 8 класс: 4 замечательные точкиСкачать

Высшая математика. 3 урок. Аналитическая геометрия. Вычисление площади треугольникаСкачать

№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать

Построение следов плоскостиСкачать

Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать

Линия пересечения плоскостейСкачать