Вопрос по геометрии:
Нужно доказать теорему.
Если площадь треугольника равна S, то площадь треугольника, составленного из его медиан, равна 3/4 S.
Заранее спасибо за Вашу помощь.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
Если площадь треугольника равна S, то площадь треугольника, составленного из его медиан, равна 3/4 S.
Заранее спасибо за Вашу помощь.
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Если площадь треугольника равна S, то площадь треугольника, составленного из его медиан, равна S
Пусть АМ, ВК, СN – медианы треугольника АВС, О – точка их пересечения.
Площадь треугольника АВО в 3 раза меньше площади треугольника АВС (высота треугольника АВО в 3 раза меньше высоты треугольника АВС).
Тогда площадь треугольника АNO равна площади треугольника АВС (медианы треугольника делят его на 6 равновеликих, то есть равных по площади, треугольников).

Мы получили, что
Построим треугольник DЕF, стороны которого равны медианам треугольника АВС.
EF = АМ, DF = ВК и DE = СN. В этом треугольнике угол DEF равен , и его площадь
Видео:Найдите площадь треугольника, если его медианы равны 3, 4 и 5Скачать
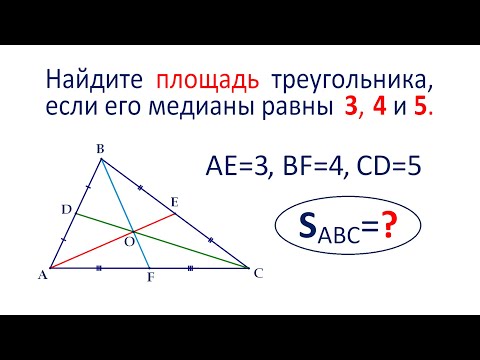
Медиана делит площадь треугольника пополам
Медиана делит площадь треугольника пополам
Два треугольника называются равновеликими. Если они имеют одинаковую площадь.
Теорема 1. Медиана делит треугольник на два равновеликих треугольника.
Пусть ВМ – медиана треугольника АВС. Докажем, что

Проведем высоту BH треугольника АВС. Тогда


Так как ВМ – медиана треугольника АВС, то АМ=МС, поэтому



Что и требовалось доказать.
Теорема 2. Медианы треугольника разбивают его на шесть равновеликих треугольников.
Доказательство можно посмотреть, например, в методическом пособии «Опорные задачи по планиметрии».
Из теоремы, в частности следует, что если точку пересечения медиан треугольника соединить со всеми его вершинами, то треугольник разобьется на три равновеликие части.
Задача 1 Две медианы треугольника взаимно перпендикулярны и равны соответственно 3 и 4. Найти площадь треугольника.
Пусть в треугольнике АВС медианы АМ и ВЕ равны 3 и 4 соответственно, 


Так как треугольник АВК прямоугольный с прямым углом ВКА, то 
Так как медиан делят треугольник на 6 равновеликих частей, то 
Задача 2 Медианы треугольника равны 6, 8 и 10, найти площадь треугольника.
Пусть медианы АM, BE и CD данного треугольника соответственно равны 6, 8 и 10, К – точка их пересечения. Отложим на продолжении луча ВЕ за точку Е отрезок EF=KE. Соединим точки С, F и A.
Рассмотрим треугольник KAF.

то

Далее, 

Так как 


Вычислим площадь треугольника AKF:

Теперь сравним площади треугольников AKF и АВС: так как AE – медиана треугольника AKF, то




Отметим, что задачу можно решить по-другому, если воспользоваться тем фактом, что:
площадь треугольника, образованного медианами данного треугольника составляет 
Доказательство можно посмотреть, например, в методическом пособии «Опорные задачи по планиметрии».
Вопросы для самопроверки:
1. Какие треугольники называются равновеликими?
2. Площадь треугольника равна S. Чему равна площадь каждого из треугольников, на которые его разбивает медиана, проведенная к какой-либо стороне этого треугольника?
3. На сколько равновеликих частей разбивают треугольник проведенные в нем три медианы?
4. Площадь треугольника равна S. Цент тяжести этого треугольника соединили с его вершинами. Чему равна площадь каждого из получившихся треугольников?
5. Площадь треугольника равна 48, чему равна площадь треугольника, составленного из медиан этого треугольника?
6. Площадь треугольника, составленного из медиан некоторого треугольника равна 24, чему равна площадь треугольника?
Задачи для самостоятельного решения:
1. Две медианы треугольника взаимно перпендикулярны и равны соответственно 6 и 8. Найти площадь треугольника.
2. Медианы треугольника равны 3, 4 и 5 найти площадь треугольника.
3. Треугольник АВС, стороны которого 13 см, 14 см и 15 см, разбит на три треугольника отрезками, соединяющими точку М пересечения медиан треугольника с вершинами треугольника. Найти площадь треугольника ВМС.
4. Две стороны треугольника равны 10 и 12, а медиана, проведённая к третьей, равна 5. Найдите площадь треугольника.
📹 Видео
Площадь треугольника, построенного на векторахСкачать

ОГЭ Р-2 номер 16Скачать

9 класс, 12 урок, Теорема о площади треугольникаСкачать

Длина медианы треугольникаСкачать

Найдите площадь треугольника, если его медианы равны 12, 15 и 21.Скачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Уравнения стороны треугольника и медианыСкачать

Советская олимпиада, которую сегодня решить только 2 школьниковСкачать

Задача, которую боятсяСкачать

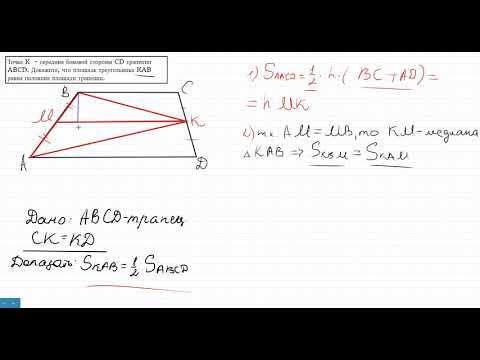
Доказать,что площадь треугольника KAB равна половине площади трапецииСкачать
Площадь параллелограмма, построенного на данных векторахСкачать

Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Формулы равностороннего треугольника #shortsСкачать

Секретные техники нахождения площади треугольника. Площадь по трём медианам / по трём высотам.Скачать

8 класс, 14 урок, Площадь треугольникаСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать








