Числовые промежутки или просто промежутки — это числовые множества, которые можно изобразить на координатной прямой. К числовым промежуткам относятся лучи, отрезки, интервалы и полуинтервалы.
- Виды числовых промежутков
- Отрезок
- Интервал и полуинтервал
- Единичная числовая окружность на координатной плоскости
- п.1. Понятие тригонометрии
- п.2. Числовая окружность
- п.3. Градусная и радианная мера угла
- п.4. Свойства точки на числовой окружности
- п.5. Интервалы и отрезки на числовой окружности
- п.6. Примеры
- Тригонометрический круг. Основные значения тригонометрических функций
- 📸 Видео
Видео:Промежутки на числовой окружностиСкачать

Виды числовых промежутков
| Название | Изображение | Неравенство | Обозначение |
|---|---|---|---|
| Открытый луч |  | x > a | (a; +∞) |
 | x 2. Открытые лучи обозначаются с помощью круглых скобок — (2; +∞), данная запись читается так: открытый числовой луч от двух до плюс бесконечности . |
Множество, которому соответствует неравенство x числовой луч от двух до плюс бесконечности и числовой луч от минус бесконечности до двух . Квадратная скобка в обозначении показывает, что точка 2 принадлежит числовому промежутку.
Видео:10 класс, 11 урок, Числовая окружностьСкачать

Отрезок
Отрезок — это множество точек прямой, лежащих между двумя граничными точками, принадлежащими данному множеству. Такие множества задаются двойными нестрогими неравенствами.
Рассмотрим отрезок координатной прямой с концами в точках -2 и 3:
Множество точек, из которых состоит данный отрезок, можно задать двойным неравенством -2 ⩽ x ⩽ 3 или обозначить [-2; 3], такая запись читается так: отрезок от минус двух до трёх .
Видео:Тригонометрическая окружность. Как выучить?Скачать

Интервал и полуинтервал
Интервал — это множество точек прямой, лежащих между двумя граничными точками, не принадлежащими данному множеству. Такие множества задаются двойными строгими неравенствами.
Рассмотрим отрезок координатной прямой с концами в точках -2 и 3:
Множество точек, из которых состоит данный интервал, можно задать двойным неравенством -2 интервал от минус двух до трёх .
Полуинтервал — это множество точек прямой, лежащих между двумя граничными точками, одна из которых принадлежит множеству, а другая не принадлежит. Такие множества задаются двойными неравенствами:
Обозначаются данные полуинтервалы так: (-2; 3] и [-2; 3). Читается это так: полуинтервал от минус двух до трёх, включая 3 , и полуинтервал от минус двух до трёх, включая минус два .
Видео:1. Числовая окружность. 10 классСкачать

Единичная числовая окружность на координатной плоскости
п.1. Понятие тригонометрии
Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов. Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., — спроектирован с использованием тригонометрии.
Базовым объектом изучения в тригонометрии является угол.
Предметом изучения тригонометрии как раздела математики выступают:
1) взаимосвязи между углами и сторонами треугольника, которые называют тригонометрическими функциями;
2) использование тригонометрических функций в геометрии.
п.2. Числовая окружность
Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.
 | Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0). Точка с координатами (1;0) является началом отсчета , ей соответствует угол, равный 0. Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным ; по часовой стрелке – отрицательным . |
| Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90°, –120°, –180°. |  |
п.3. Градусная и радианная мера угла
Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).
В целом, более обоснованной и естественной для измерения углов является радианная мера.
 | Найдем радианную меру прямого угла ∠AOB=90°. Построим окружность произвольного радиуса r с центром в вершине угла – точке O. Длина этой окружности: L=2πr. Длина дуги AB: (l_=frac=frac=frac.) Тогда радианная мера угла: $$ angle AOB=frac<l_>=frac=frac $$ |
| 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 270° | 360° |
| (frac) | (frac) | (frac) | (frac) | (frac) | (frac) | (frac) | (pi) | (frac) | (2pi) |
п.4. Свойства точки на числовой окружности
Построим числовую окружность. Обозначим O(0;0), A(1;0)
 | Каждому действительному числу t на числовой окружности соответствует точка Μ(t). При t=0, M(0)=A. При t>0 двигаемся по окружности против часовой стрелки, описывая дугу ⌒ AM=t. Точка M — искомая. При t Например: |
| Отметим на числовой окружности точки, соответствующие (frac, frac, frac, frac, pi), а также (-frac, -frac, -frac, -frac, -pi) Для этого нужно отложить углы 30°, 45°, 90°, 120°, 180° и –30°, –45°, –90°, –120°, –180° с вершиной в начале координат и отметить соответствующие дуги на числовой окружности. |  |
| Отметим на числовой окружности точки, соответствующие (frac, frac, frac), и (-frac). Все четыре точки совпадают, т.к. begin Mleft(fracright)=Mleft(frac+2pi kright)\ frac-2pi=-frac\ frac+2pi=frac\ frac+4pi=frac end |  |
п.5. Интервалы и отрезки на числовой окружности
Каждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.
| Числовой промежуток | Соответствующая дуга числовой окружности |
| Отрезок | |
$$ -frac lt t lt frac $$  а также, с учетом периода $$ -frac+2pi klt tltfrac+2pi k $$ |  |
| Интервал | |
$$ -frac leq t leq frac $$  а также, с учетом периода $$ -frac+2pi kleq tleqfrac+2pi k $$ |  |
| Полуинтервал | |
$$ -frac leq t ltfrac $$  а также, с учетом периода $$ -frac+2pi kleq tltfrac+2pi k $$ |  |
п.6. Примеры
Пример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2.
Чему равны дуги AE, BE, EC, ED в градусах и радианах?
Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: begin BE=30^=frac.\ EC=60^=frac.\ AE=EC+CD=90^+30^=120^=frac.\ ED=EC+CD=60^+90^=150^=frac. end
Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: (-frac; frac; frac; frac).
| Находим соответствующие углы в градусах и откладываем с помощью транспортира (положительные – против часовой стрелки, отрицательные – по часовой стрелке), отмечаем соответствующие точки на числовой окружности. begin -frac=-90^, frac=135^\ frac=210^, frac=315^ end |  |
Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: (-frac; 5pi; frac; frac).
| Выделяем из дроби целую часть, отнимаем/прибавляем один или больше полных оборотов (2πk — четное количество π), чтобы попасть в промежуток от 0 до 2π. Далее – действуем, как в примере 2. begin -frac=fraccdotpi=-6pi+fracrightarrow frac=90^\ 5pi=4pi+pirightarrow pi=180^\ frac=fracpi=3pi-fracrightarrow pi-frac=frac\ frac=fracpi=7pi-fracrightarrow pi-frac=frac end |  |
Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.
 | Сравниваем каждое число с границами четвертей: begin 0, fracpi2approxfrac=1,57, piapprox 3,14\ 3pi 3cdot 3,14\ fracapprox frac=4,71, 2piapprox 6,28 end |
(fracpi2lt 2lt pi Rightarrow ) угол 2 радиана находится во 2-й четверти
(pilt 4lt frac Rightarrow ) угол 4 радиана находится в 3-й четверти
(fraclt 5lt 2pi Rightarrow ) угол 5 радиана находится в 4-й четверти
(7gt 2pi), отнимаем полный оборот: (0lt 7-2pilt fracpi2Rightarrow) угол 7 радиан находится в 1-й четверти.
Пример 5. Изобразите на числовой окружности множество точек ((kinmathbb)), запишите количество полученных базовых точек.
| $$ frac $$ | $$ -frac+2pi k $$ |
 Четыре базовых точки, через каждые 90° |  Две базовых точки, через каждые 180° |
| $$ frac+frac $$ | $$ -frac $$ |
 Три базовых точки, через каждые 120° |  Пять базовых точек, через каждые 72° |
Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

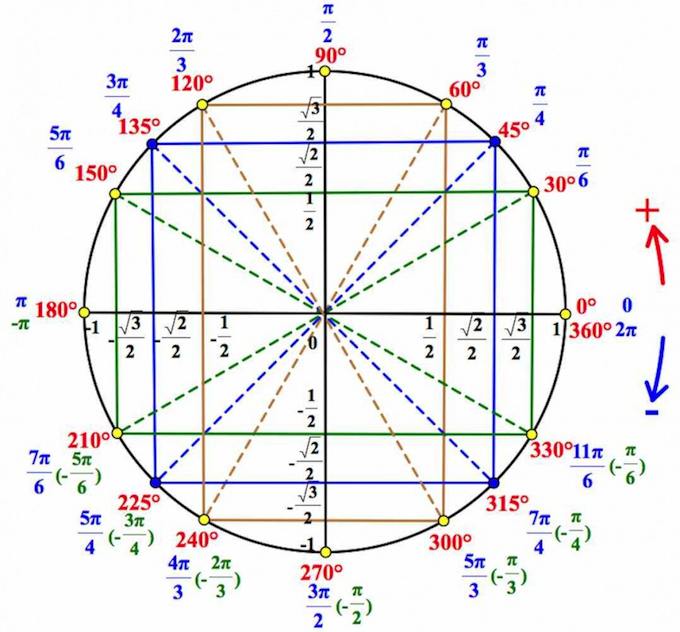
Тригонометрический круг. Основные значения тригонометрических функций
Если вы уже знакомы с тригонометрическим кругом , и хотите лишь освежить в памяти отдельные элементы, или вы совсем нетерпеливы, – то вот он, тригонометрический круг :
Мы же здесь будем все подробно разбирать шаг за шагом + показать
Тригонометрический круг – не роскошь, а необходимость

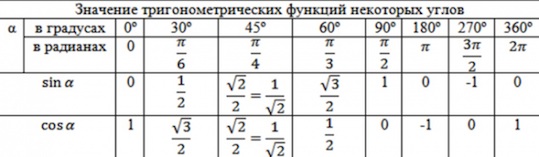
Очень важно не махать рукой на значения тригонометрических функций, – мол, всегда можно посмотреть в шпору с таблицей значений.
Если вы постоянно смотрите в таблицу со значениями тригонометрических формул, давайте избавляться от этой привычки!
Нас выручит тригонометрический круг ! Вы несколько раз поработаете с ним, и далее он у вас сам будет всплывать в голове. Чем он лучше таблицы? Да в таблице-то вы найдете ограниченное число значений, а на круге – ВСЕ!
К примеру, скажите, глядя в стандартную таблицу значений тригонометрических формул , чему равен синус, скажем, градусов, или
.
Никак. можно, конечно, подключить формулы приведения… А глядя на тригонометрический круг, легко можно ответить на такие вопросы. И вы скоро будете знать как!
А при решении тригонометрических уравнений и неравенств без тригонометрического круга – вообще никуда.
Знакомство с тригонометрическим кругом
Давайте по порядку.
Сначала выпишем вот такой ряд чисел:
И, наконец, такой:
Конечно, понятно, что, на самом-то деле, на первом месте стоит , на втором месте стоит
, а на последнем –
. То есть нас будет больше интересовать цепочка
.
Но как красиво она получилась! В случае чего – восстановим эту «лесенку-чудесенку».
И зачем оно нам?
Эта цепочка – и есть основные значения синуса и косинуса в первой четверти.
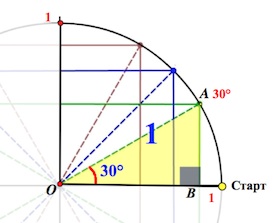
Начертим в прямоугольной системе координат круг единичного радиуса (то есть радиус-то по длине берем любой, а его длину объявляем единичной).
От луча «0-Старт» откладываем в направлении стрелки (см. рис.) углы .
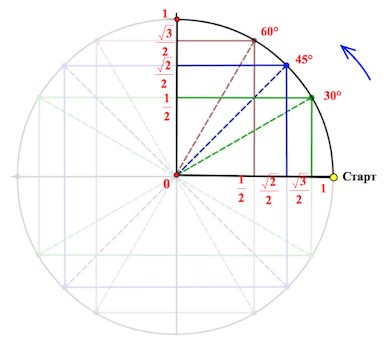
Это почему же, спросите вы?
Не будем разбирать все. Рассмотрим принцип, который позволит справиться и с другими, аналогичными ситуациями.
Треугольник АОВ – прямоугольный, в нем . А мы знаем, что против угла в
лежит катет вдвое меньший гипотенузы (гипотенуза у нас = радиусу круга, то есть
).
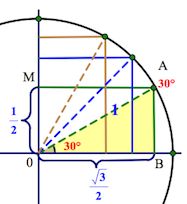
Значит, АВ= (а следовательно, и ОМ=
). А по теореме Пифагора
Надеюсь, уже что-то становится понятно?
Так вот точка В и будет соответствовать значению , а точка М – значению
Аналогично с остальными значениями первой четверти.
Как вы понимаете, привычная нам ось (ox) будет осью косинусов , а ось (oy) – осью синусов . Про тангенс и котангенс позже.
Слева от нуля по оси косинусов (ниже нуля по оси синусов) будут, конечно, отрицательные значения.
Итак, вот он, ВСЕМОГУЩИЙ тригонометрический круг , без которого никуда в тригонометрии.
А вот как пользоваться тригонометрическим кругом, мы поговорим в следующей статье.
📸 Видео
ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Числовая окружностьСкачать

Как искать точки на тригонометрической окружности.Скачать

10 класс - Алгебра - Числовая окружностьСкачать

ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

Математическая модель - числовая окружностьСкачать

10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

9 класс, 2 урок, Множества и операции над нимиСкачать

АЛГЕБРА 10 класс: Числовая окружность. Общие понятия | ВидеоурокСкачать

Соответствие чисел точкам числовой окружностиСкачать

Макеты числовой окружностиСкачать

10 класс. Алгебра. Числовая окружность.Скачать

Числовая окружность 10 класс АлимовСкачать

Длина дуги числовой окружности | Алгебра 10 класс #9 | ИнфоурокСкачать