Окружность и овал кассини

Виктор Чебыкин
Инженер, Новосибирск

Овалы (от фр. ovale — овал) — замкнутые выпуклые плоские кривые. При этом под выпуклостью понимают свойство кривой иметь с любой прямой не более двух (действительных) общих точек [1].

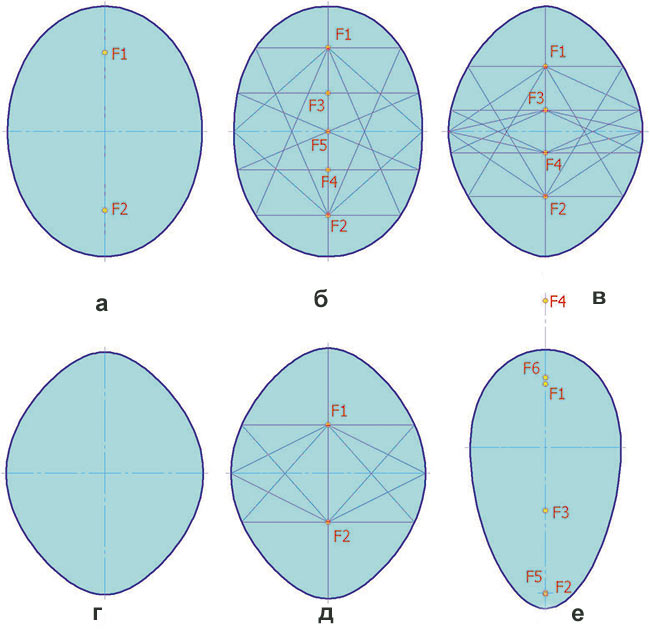
На рис. 1 изображены шесть овальных кривых, на первый взгляд очень похожих между собой (за исключением 1е).

Видео:Как начертить овал. Эллипс вписанный в ромбСкачать

Эллипс

Эту кривую (рис. 1а) знают практически все — это эллипс. Первые упоминания о нем датируются несколькими веками до н.э. Главные свойства эллипса: кривая имеет два фокуса; все лучи, исходящие из одного фокуса, отражаясь от кривой, собираются во втором фокусе и наоборот; сумма отрезков от любой точки кривой до фокусов есть величина постоянная. Значение эллипса трудно переоценить — его геометрия и свойства используются как природой, так и человеком.

Рис. 1. Овальные кривые: а — эллипс; б — овал Кассини; в — кривая Ламе; г — кривая R-0; д — кривая R-1; е — кривая R-2

Видео:Изображение окружности в перспективе. Эллипс.Скачать

Овал Кассини

Еще одну кривую (рис. 1б) предложил астроном Джованни Кассини в XVII веке. Он полагал, что именно по такой траектории движутся планеты Солнечной системы, в чем, как выяснилось, заблуждался.

Овал Кассини — геометрическое место точек, произведение расстояний от которых до фокусов постоянно. Свойства кривой: овал Кассини не всегда имеет эллипсовидную форму и может трансформироваться в точки, совпадающие с фокусами; в два яйцевидных овала; в лемнискату; в окружность… Свойства кривой в диапазоне овалов: наличие двух основных фокусов F1 и F2, а также трех дополнительных фокусов F3, F4, F5, один из которых совпадает с центром кривой. Две пары лучей, исходящих из фокусов F3 и F4, отраженных от кривой, проходят через центр F5, и после второго отражения от кривой попадают в противоположные фокусы. Таких дополнительных фокусов больше нет ни у одной из описываемых в статье кривых.

Овалы Кассини используются в теории упругости, в конструкциях антенн; установлено геометрическое подобие овалов с формой силовых линий некоторых электромагнитных полей.

Видео:КАК НАРИСОВАТЬ КРУГ В ИЗОМЕТРИИ (ОВАЛ В ИЗОМЕТРИЧЕСКОЙ ПРОЕКЦИИ).Скачать

Кривая Ламе

Кривая Ламе (рис. 1в) предложена Габриелем Ламе в XIX веке.

, (1)

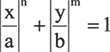
Формула на вид проста, но при изменении параметров кривая может кардинально менять свою форму (рассматриваем только эллипсовидные формы овала). В отличие от овала Кассини, кривая всегда непрерывна. Еще одно свойство кривой: при разных сочетаниях m, n, a, b она может иметь два либо четыре фокуса или не иметь их вообще. Это свойство наблюдалось в диапазоне значений степеней n и m от 1,5 до 2.

Кривая Ламе (суперэллипс) используется в архитектуре (стадион в Мехико), в дорожном строительстве (площадь с фонтаном в Стокгольме), в дизайне мебели и др.

Следующие три овальные кривые не входят в линейку известных, но, поскольку имеют явное практическое значение (применение) и ряд собственных характерных свойств, также заслуживают упоминания (кривая R­0) или описания и сравнения с известными (кривые R­1 и R­2). Геометрия кривых определена с помощью трехмерных сборок обечайка — люк, выполненных в КОМПАС­3D.

Видео:Овал по заданным осям . Геометрические построения.Скачать

Кривая R­0

Овальная кривая R­0 (рис. 1г) получена в результате разворачивания на плоскость фигуры пересечения круглого цилиндрического люка с круглой цилиндрической обечайкой резервуара при S ® 0, где S — толщина стенки обечайки, определяющая геометрию отверстия. Люк установлен перпендикулярно продольной оси резервуара без смещения. Поскольку применимость ее незначительна, ограничимся лишь определением: плоская гладкая замкнутая эллипсовидная бесфокусная овальная кривая.

Видео:Как начертить овал в профильной плоскостиСкачать

Кривая R­1

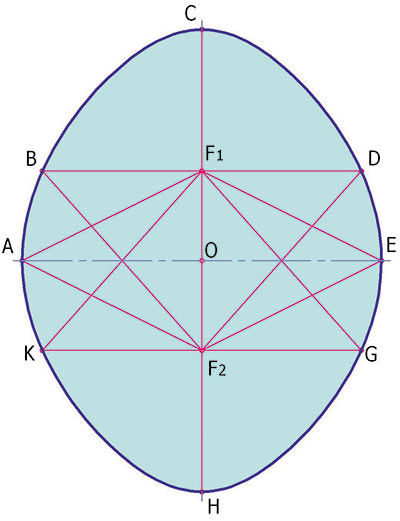
Кривая R­1 (резервуарный овал 1­го рода) (рис. 1д и рис. 2) предложена и описана впервые в статье [2].

Кривая R­1 — это плоская гладкая замкнутая эллипсовидная двухфокусная овальная кривая. Кривая получена в результате разворачивания на плоскость фигуры пересечения круглого цилиндрического люка (патрубка) с круглой цилиндрической обечайкой толщиной S -> 0 с учетом гарантированного зазора D и определяет геометрию отверстия в обечайке. Люк установлен перпендикулярно продольной оси резервуара без смещения от нее.

Следует обратить внимание на большую схожесть кривой R­1 с кривой Ламе (рис. 1в). Эта схожесть не случайна. Автор пытался подогнать кривую Ламе к кривой R­1 методом последовательного приближения. Попытка не удалась — кривые не сходились, кроме того, имели разное количество фокусов. Вывод — кривая R­1 не является частным случаем кривой Ламе.

Одним из важных свойств овальных кривых R­1 является наличие двух (и только двух) фокусов во всем возможном диапазоне сочетаний параметров: диаметр обечайки, диаметр люка, толщина обечайки, гарантированный зазор. «Гуттаперчевая» кривая Ламе таким свойством не обладает, обращаясь с фокусами более вольно.

Фокусы кривой R­1 могут обменяться между собой восемью парами лучей, отраженных от кривой, и парой прямых лучей. У эллипса, как известно, все лучи от одного фокуса собираются в противоположном.

Овал R­1 обладает еще одним свойством: вышеупомянутые лучи делят кривую овала на восемь частей. Точки падения этих лучей на кривую являются характерными точками, в которых меняется знак роста суммы пары отрезков от точки кривой до фокусов на противоположный (см. рис. 2). Интервалы кривой с положительными и отрицательными знаками чередуются. У эллипса, как известно, сумма отрезков от любой точки контура до фокусов есть величина постоянная.

Рис. 2. Овальная кривая R-1

Приведеные здесь формулы* служат для определения большой и малой осей этой овальной кривой:

; (2)

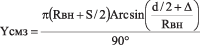
где: Yсмз — большая ось овала (смз здесь и далее — соединение с минимальными зазорами);

Rвн — внутренний радиус обечайки резервуара;

S — толщина стенки обечайки резервуара;

d — наружный диаметр люка;

△ — гарантированный зазор между обечайкой и люком в любой точке сопряжения (периметральный зазор);

Xсмз — малая ось овала.

Видео:КАК РИСОВАТЬ ЭЛЛИПСЫ. Простой и быстрый способ рисования ЭЛЛИПСОВСкачать

Кривая R­2

Кривая R­2 (резервуарный овал 2­го рода) (рис. 1е, рис. 3 и 4) предложена и описана в статье [2].

Кривая R­2 —это плоская замкнутая яйцевидная шестифокусная овальная кривая. Кривая получена в результате разворачивания на плоскость фигуры пересечения круглого цилиндрического люка (патрубка) с круглой цилиндрической обечайкой резервуара с толщиной стенки S>0 с учетом гарантированного зазора △ и определяет геометрию отверстия в обечайке. Ось люка перпендикулярна продольной оси резервуара. Люк установлен со смещением от этой оси.

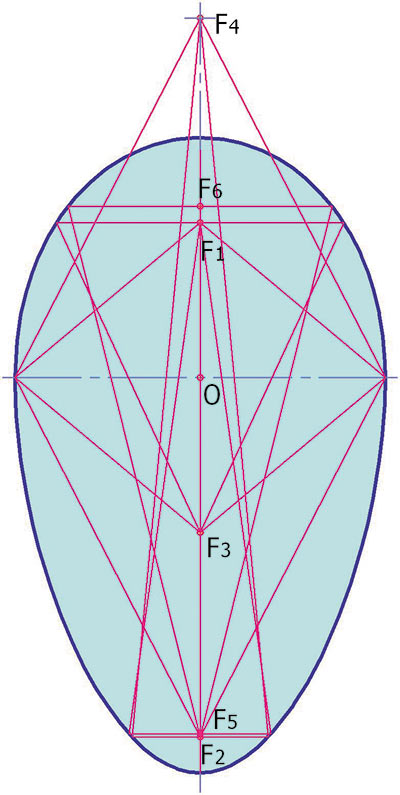
Овал R­2 имеет яйцевидную форму. Характерным свойством овала R­2 является наличие шести фокусов (см. рис. 3).

Рис. 3. Овальная кривая R-2

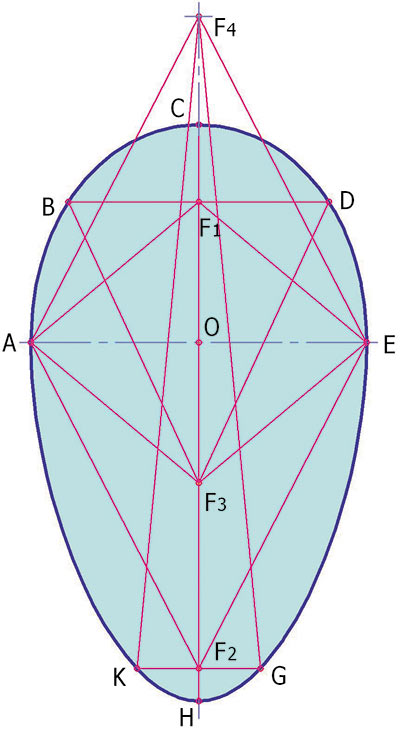
Рис. 4. Овальная кривая R-2. Характерные точки

Рис. 5. Резервуар

(4)

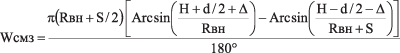
Шесть лучей, выпущенные из фокуса F1, отраженные от кривой, собираются в противоположном ему фокусе F3 и, наоборот, фокусы F2 и F4 связаны между собой пятью парами отраженных лучей, пары фокусов F1­F5 и F2­F6 могут обменяться между собой только четырьмя парами отраженных лучей.

Сумма отрезков, соединяющих точки на кривой с фокусами F1 и F2, непостоянна и растет по мере отдаления от полюса H и приближения к полюсу C (см. рис. 4). Сумма отрезков, соединяющих точки на кривой с фокусами F1 и F3, непостоянна и имеет смену знака роста в характерных точках A, B, С, D, E, H. Сумма отрезков, соединяющих точки на кривой с фокусами F2 и F4, также непостоянна и имеет смену знака роста в точках A, C, E, G, H, K.

Еще одно свойство: точки A и E являются точками перелома кривой, в связи с чем кривая не относится к гладким.

Этими свойствами кривая отличается как от R­1, так и от эллипса.

Размеры осей овальной кривой R­2 можно определить по формулам (4) и (5),где: Wсмз — большая ось овала;

Xсмз — малая ось овала;

H — смещение оси люка от продольной оси резервуара.

Проверка геометрии полученных кривых в 3D­моделлере: на 3D­модели обечайки в развернутом состоянии вырезали по полученной кривой отверстие, после чего обечайку сворачивали в круговой цилиндр и соединяли с моделью люка. Далее с этой 3D­сборки создавался чертеж — вид сверху, на котором проводились измерения. Результат проверки следующий: отклонение от заданного гарантированного зазора не превышало нескольких сотых миллиметра (кривая была выполнена сплайном по 40 точкам). При увеличении количества опорных точек точность построения возрастает.

Кривые проверены непосредственно при разработке и изготовлении резервуаров и показали свою состоятельность. С использованием овальных кривых R­1 и R­2 изготовлено уже несколько сотен резервуаров, при этом ни одного случая плохой стыковки обечайки с люком не зафиксировано, что окончательно доказывает правильность их геометрии.

На рис. 5 показан один из резервуаров, конструкция которого выполнена с использованием кривой R­1.

Видео:Как быстро начертить идеальный овал? #ShortsСкачать

Выводы

Все описанные в статье овальные кривые, благодаря своим оригинальным свойствам и геометрии, имеют практическое применение, иногда отличающееся от первоначально задуманного (овал Кассини).

Расширена линейка известных овальных кривых. Предложены и описаны «резервуарные» овалы 1­го и 2­го рода (овальные кривые R­1 и R­2), назначение которых определяется объединяющим их термином.

Видео:ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

Библиографический список

1. Большая Советская Энциклопедия. М.: Советская Энциклопедия, 1969­1978.
2. Чебыкин В.Г. Врезка люков в обечайки резервуаров, соединения с минимальными (гарантированными) зазорами. Новые виды овальных кривых — «резервуарные» овалы // Справочник. Инженерный журнал. 2012. № 11. С. 31­33.

*Формулы, приведенные в статье, кроме формулы кривой Ламе, выведены автором.

Видео:Эллипс - Инженерная графика.Скачать

Астроида

Астроида — плоская кривая, описываемая точкой M окружности радиуса r, катящейся по внутренней стороне окружности радиуса R = 4r. Иначе говоря, астроида — это гипоциклоида с модулем m = 4.

Уравнение в декартовых прямоугольных координатах:

| x | 2 / 3 + | y | 2 / 3 = R2 / 3

x = Rcos3t y = Rsin3t

· Длина дуги от точки с 0 до

• · Длина всей кривой 6R.
• · Радиус кривизны:

· Площадь, ограниченная кривой:

• · Астроида является огибающей семейства отрезков постоянной длины, концы которых расположены на двух взаимно перпендикулярных прямых.
• · Астроида является алгебраической кривой 6-го порядка.

Видео:1 2 4 сопряжение окружностейСкачать

Овал Кассини

Овал Кассини — геометрическое место точек, произведение расстояний от которых до двух заданных точек (фокусов) постоянно и равно квадрату некоторого числа a.

Частным случаем овала Кассини при фокусном расстоянии равном 2a является Лемниската Бернулли. Сам овал является лемнискатой с двумя фокусами.

Кривая была придумана астрономом и инженером Кассини. Он ошибочно считал, что она точнее и определяет орбитуЗемли, чем эллипс[1].

Расстояние между фокусами 2c.

· В прямоугольных координатах:

Фокусы — F1( ? c;0) и F2(c;0). Возьмём произвольную точку M(x;y), найдём расстояние от фокусов до неё и приравняем его к a2:

Возводим в квадрат обе части равенства:

Раскрываем скобки в левой части:

Раскрываем скобки, свёртываем новый квадрат суммы и выносим общий множитель:

· Явное уравнение в прямоугольных координатах:

· В полярной системе координат:

Чёрная окружность — множество максимумов и минимумов; синяя лемниската — множество точек перегиба

• · Овал Кассини — алгебраическая кривая четвёртого порядка.
• · Она симметрична относительно середины отрезка между фокусами.
• · Приимеет два абсолютных максимума и два минимума:

Геометрическое место точек абсолютных максимумов и минимумов — окружность радиуса c с центром в середине отрезка между фокусами.

· Прикривая имеет четыре точки перегиба. Их полярные координаты:

Геометрическое место точек перегиба — лемниската с вершинами .

· Радиус кривизны для представления в полярных координатах:

Видео:Ovals Of CassiniСкачать

Окружность и овал кассини

Полный вариант статьи ищите на сайте АРБУЗ — занимательный мир

Космические овалы Кассини

Напомним определение эллипса – это плоская фигура, у которой для каждой точки сумма расстояний от двух фиксированных точек (полюсов) постоянна. От соотношения расстояний между фокусами и этой суммы расстояний (или от соотношения полуосей) можно получить разные фигуры – от круга до (постепенно сплющиваясь) вырождения в линию.

Занимательные задачи, связанные с эллипсом основаны на его отражательных свойствах – лучи, выйдя из одного фокуса, обязательно соберутся в другом. А если не из фокуса? У Мартина Гарднера рассматривается бильярдный стол в форме эллипса. Так вот, если послать шар так, чтобы он не пересек отрезок между фокусами, то он так и будет кататься, не пересекая этот отрезок, заметая поверхность вокруг воображаемого эллипса меньших размеров. Если же послать шар (из произвольной точки) так, чтобы он пересек отрезок между фокусами эллипса, то он так и будет двигаться, каждый раз пересекая этот отрезок и касаясь двух воображаемых ветвей гипербол с фокусами в фокусах эллипса. Желающие могут реализовать эту забаву в виде программы.

А еще можно в уравнении эллипса x 2 / a 2 + y 2 / b 2 = r 2 попробовать поменять показатель степени, брать не 2, а от 0 до, предположим, 10, прорисовать совместно и проследить, как меняется форма от ромба до прямоугольника.

Пока на время распрощаемся с эллипсом. Теперь представьте любителя математики рассматривающего определение эллипса… Вполне естественно, что у него мелькнет мысль – а что, если постоянным будет не сумма расстояний от двух точек, а их произведение? Не поленитесь, попробуйте – напишите формулы расстояний от текущей точки с координатами x, y до фокусов (-а,0) и (а,0), перемножьте их и попробуйте привести полученное уравнение четвертой степени к «красивому» виду. Это уравнение и соответствует так называемым овалам Кассини. Знаете почему?

в 1680 Джовани Кассини изучал кривую Кассиниану, которая является геометрическим местом точек, чье произведение расстояний от двух фиксированных фокусов постоянно. Он работал над этой кривой в процессе изучения относительных движений Земли и Солнца и предложил это как кривая для планетарных орбит подходит больше, чем эллипс, предложенный Кеплером. Открытая чуть позже лемниската Якоба Бернулли была частным случаем овала Кассини, но это не было осознано математиками в течение ста лет.

Итак, мы записали произведение расстояний от двух фокусов:

где a – половина расстояния между фокусами, а b 2 – и есть величина этого самого произведения. После раскрытия скобок и приведения подобных членов мы получим уравнение овалов в классическом виде:

Теперь мы можем проделать опыт, который мы делали в статье про улитку Паскаля – перенесем свободный член влево от знака равенства, но приравняем полученный многочлен не нулю, а некоторой переменной k, из которой мы получим значения красной, синей и зеленой составляющей цвета. Запуcтив процесс в цикле по координатам x и y, мы сразу получим потрясающий рисунок.

Рассмотрим получившуюся картинку. Мы видим на ней как обычные овалы при движении от периферии к центру начинают сужаться, появляется утоньшение посередине и потом перемычка, потом рисунок распадается на две части. Все эти кривые и есть семейство овалов Кассини. А вид их зависит от соотношения параметров a и b.

При значениях b > a * sqr(2) фигура выпуклая как эллипс.

При b =а* sqr (2)появляются прямые участки, фигура имеет вид как на рисунке слева.

При а b фигура разваливается на два овала.

То есть, на нашем первом рисунке мы сразу получили все семейство овалов Кассини.

С чего же мы начнем наши попытки нарисовать овалы Кассини по настоящему, чтобы поиграть с ними? Для рисования функции необходимо или явно выразить одну переменную через другую – но для этого пришлось бы решать уравнение четвертой степени, либо задать обе координаты в параметрическом виде – мне не встретилось нигде такое представление овалов Кассини. Или же, третий вариант, нарисовать все в полярных координатах, тем более что формула относительно не сложная:

Причем, сразу начнем с экспериментов – нарисуем не один овал, а в цикле будем менять параметр a (напомню — половина межфокусного расстояния). И результат:

Обратите внимание, как «расползался» овал от окружности (а=0) до Лемнискаты Бернулли (a = b ). И код этого чуда с глазами и ушами:

Оба подкоренных выражения вынесены в отдельные вспомогательные переменные с проверкой на положительность, впрочем, это технические мелочи.

Обратите внимание на раскраску – красная, синяя и зеленая составляющие привязаны к параметру f – центральному углу, что и дает радужные радиальные полосы. Можно было привязаться и к текущему радиусу или к комбинации угла и радиуса, попробуйте сами. А мы пока зададимся естественно вытекающим из предыдущего опыта вопросом – а что, если менять в цикле не фокусные расстояния, а радиус (точнее значение произведения двух радиусов), или, в наших обозначениях, переменную b. Сказано – сделано:

Мы снова получили, как и на первом рисунке семейство овалов Кассини с фиксированными фокусами. Доработка кода была минимальной – вместо цикла по переменной а (межфокусное расстояние) запустили цикл по переменной b (произведение радиусов). Вот и код:

Все ли хорошо? Нет… смущает пустота в распавшихся на две части зонах… Цикл специально прерывался (точнее, начинался) при значении a = b, ибо при попытке прорисовать распадающиеся части выявляются неопознанные артефакты:

Рисунок, конечно, сам по себе красивый, но мы-то движемся к намеченной цели, а тут – неизвестно что. (Код такой же, как и в предыдущем случае, только внешний цикл имеет вид «For b = a To 0 Step -6»). Во-первых – не прорисованы внутренние зоны обоих овалов, а во-вторых – непонятные вылезания «наружу». Как избавиться от глюков? Первая мысль – неправильно отрабатывает синус, ибо, кто же винит в первую очередь себя? Потом станет стыдно за такие мысли… Но что делать? Морщим лоб, чешем репу в наивной попытке озарения…

Ну, конечно же – надо брать оба знака после вычисления квадратного корня, а у нас был предусмотрено только положительное значение… засучиваем рукава и… так и есть – начали прорисовываться внутренние области. В программе это реализовано вводом вспомогательных переменных k и j, которые постоянно меняют свой знак, а так, как мы проверяем знак подкоренного выражения, то к ошибке это не приводит, зато выводит внутренние области овалов. Для избавления от «вылезаний наружу» тоже находится средство – при построении развалившихся областей надо давать ограничения по полярному углу.

Но в Visual Basic’e (и в других популярных языках программирования) нет арксинуса, есть только арктангенс. Поэтому формулу чуть-чуть дорабатываем и имеем желанный результат:

Вот они, эти глаза из космоса, в виде кода:

Естественно, что при определении границ существования углов надо не забыть и о втором овале, обычно о нем вспоминают после первого «одноглазого» рисунка. Для достоверности пришлось ввести коэффициент 0,42 – так как формула была приведена для овала единичного радиуса без учетов нашего масштаба.

Что еще интересного, спросите далее? Есть красивые продолжения. Дело в том, что рассмотренные овалы с двумя фокусами всего лишь частный случай овалов Кассини, обобщенных на произвольное количество фокусов. Это обобщение открыл и исследовал в 1843 году Серрет (Serret) и он же назвал все множество именем великого астронома.

И код программы:

Хотелось бы извиниться за использование одной и той же буквы, но думаю ясно, что в последних формулах «а» – это не межфокусное расстояние, как раньше, а масштабный коэффициент, учитывающий, что формулы даны для единичного радиуса. Тут же даем количество фокусов n равное трем:

И не в силах остановиться… это то же вихрь, который захватывает при рисовании циклоид и фигур Лиссажу, например, даем n=1.5

Все, усилием воли останавливаем эти чудесные опыты.

Еще три красивых, этюдных, момента.

Лемниската Бернулли

Лемнискату Бернулли можно определить как геометрическое место точек, для которых произведение расстояний от двух фокусов равно квадрату половины расстояния между фокусами. Великий физик описал эту «похожую на 8 поверхность» в своей статье Acta Eruditorumon, вышедшей в 1694 году. К сожалению, он не знал, что его лемниската – частный случай овалов, описанных Кассини четырнадцатью годами ранее.

Лемнискату Бернулли можно также рассматривать как частный случай циссоиды. Определения циссоиды давать не будем, лучше сразу рассмотрим на примере.

Выберем точку О, отстоящую от центра окружности с единичным радиусом на расстояние sqrt(2) и проведем из нее линию, пересекающую окружность в точках Q1 и Q2. Теперь сдвинем отрезок Q1Q2 вдоль линии до совмещения точки Q1 с точкой О. При движении отрезка точка Q2 будет рисовать циссоиду, в данном случае лемнискату Бернулли.

Спросите, чему равна площадь одного крыла бабочки лемнискаты Бернули? Если а – половина фокусного расстояния, то S = a 2 (. ) без всяких там Пи и прочих коэффициентов, словно это обычная квадратная табуретка!

Вот простейший пример лемнискаты Бернулли

А знаете ли вы, какая фигура получится при разрезании тора (бублика)? Правильно – овалы Кассини.

И последней не совсем серьезной темой, имеющей отдаленное отношение к овалам Кассини, будет теория яиц. Или, точнее, яйцевидных поверхностей. Собственно, поверхностью они станут после вращения вокруг продольной оси, а пока займемся поисками самого подходящего сечения. Самый простой способ – в определении эллипса ввести поправочку и рассматривать постоянство суммы расстояний от двух фокусов, но с учетом того, что расстояние от одного из фокусов умножается на постоянный коэффициент. Не поленитесь, попробуйте вывести уравнение яйцевидного эллипса и прорисовать при разных значениях искажающего коэффициента. Вряд ли вы найдете более интересное и востребованное времяпрепровождение. Куры должны быть благодарны аналитической геометрии. (Уравнение получится, предупреждаю, громоздким. По этой же причине не получилось исказить таким же образом овалы Кассини, хотя очень хотелось попробовать)

Разработаны различные методики яйцевидного искажения эллипсов. Одна из них задается уравнением (в символах Бейсика) X ^ 2 +(1.4 x *1.6*y) 2 =1 для круга единичного радиуса, или равно R 2 в общем случае, откуда Y = sqr(R 2 — X 2 )/( R *1.6*1.4 x ). В общем-то, коэффициент 1.4 сразу вызвал подозрение, и решено было менять его в цикле, как показали опыты, от 1 до 1.007 с шагом 0.001, что вы и видите на картинке.

А вот и код этого набора яиц. Переменная n вспомогательная для раскраски.

Продолжая эти столь важные для науки опыты, мы опытным путем находим идеальное значение возводимого в степень х коэффициента: 1.0014. Запомните это число и посмотрите на совершенную форму яйца, порождаемого им. Осталось только начать вращать его вокруг продольной оси, получить каркас, натянуть на него поверхность, дать тени и блики… и можно незаметно подложить наседке.

📺 Видео

Как начертить овал. Уроки черчения.Скачать

📖 Óvalos de Cassini #clasmat #visualization #math #goemetryСкачать

Круг в перспективеСкачать

Как легко нарисовать овал. DIYСкачать

Построение овалаСкачать

Черчение, построение овала в аксонометрииСкачать

Рисуем Овал для расположения светильниковСкачать

Построение касательной к окружностиСкачать

Как начертить овал в горизонтальной плоскостиСкачать