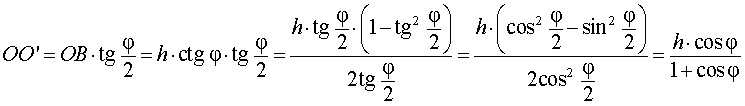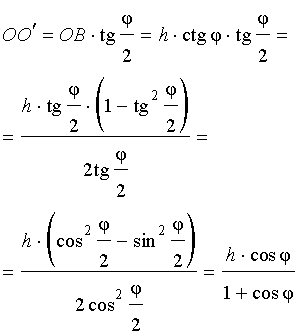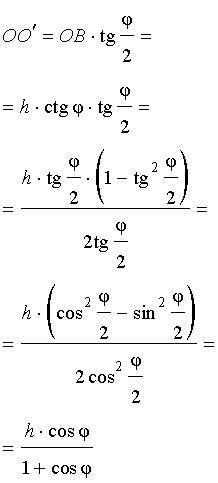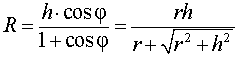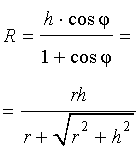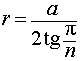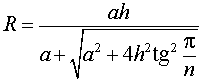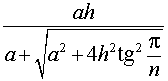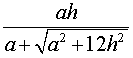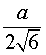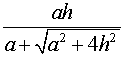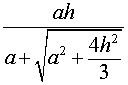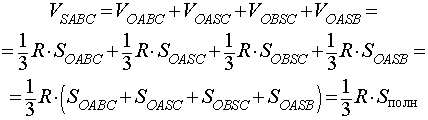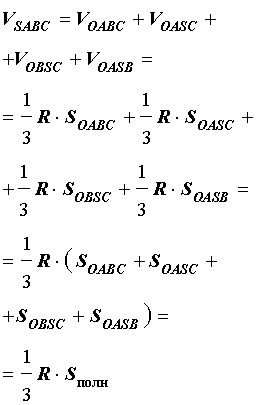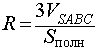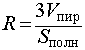Центр вписанной окружности в тетраэдре (5 видео)

Сфера, вписанная в пирамиду

Биссекторная плоскость. Основное свойство биссекторной плоскости

Сфера, вписанная в пирамиду. Свойства пирамиды, описанной около сферы

Радиус сферы, вписанной в правильную n — угольную пирамиду

Сфера, вписанная в треугольную пирамиду. Формула для радиуса вписанной сферы

Содержание

Биссекторная плоскость. Основное свойство биссекторной плоскости
Сфера, вписанная в пирамиду. Свойства пирамиды, описанной около сферы
Радиус сферы, вписанной в правильную n — угольную пирамиду
Сфера, вписанная в треугольную пирамиду. Формула для радиуса вписанной сферы
Центр вписанной окружности в тетраэдре
Тетраэдр.
Свойства тетраэдра.
Типы тетраэдров.
Формулы для определения элементов тетраэдра.
📽️ Видео

Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Биссекторная плоскость. Основное свойство биссекторной плоскости

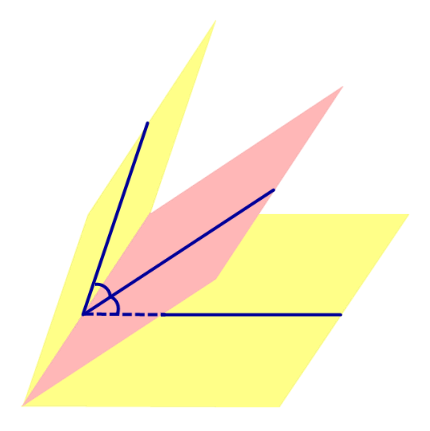
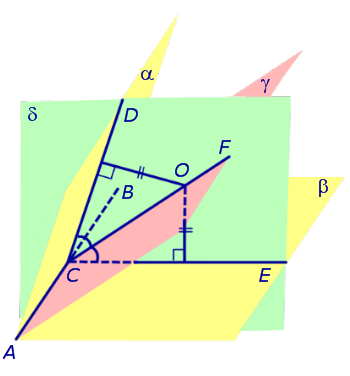
Определение 1. Биссекторной плоскостью двугранного угла называют такую плоскость, которая проходит через ребро двугранного угла и делит этот угол на два равных двугранных угла (рис. 1).

Утверждение 1. Точка, расположенная внутри двугранного угла, находится на одном и том же расстоянии от граней этого угла тогда и только тогда, когда она лежит на биссекторной плоскости.

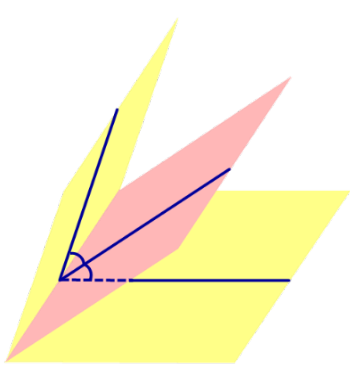
Доказательство. Рассмотрим произвольную точку O, расположенную внутри двугранного угла, и проведем через эту точку плоскость δ , перпендикулярную к ребру AB двугранного угла (рис. 2).

Плоскость δ пересекает ребро AB двугранного угла в точке C, а грани двугранного угла α и β по лучам CD и CE соответственно. Угол DCE является линейным углом двугранного угла. Биссекторная плоскость γ пересекает плоскость δ по биссектрисе CF линейного угла DCE .

Таким образом, справедливость утверждения вытекает из соответствующих теорем о свойствах биссектрисы угла. Доказано.

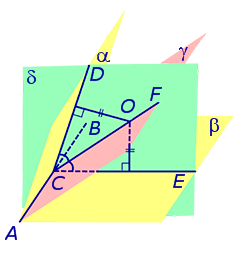
Следствие 1. Если сфера, расположенная внутри двугранного угла, касается каждой из плоскостей граней этого угла, то центр сферы находится на биссекторной плоскости двугранного угла (рис. 3).

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Сфера, вписанная в пирамиду. Свойства пирамиды, описанной около сферы

Определение 2. Сферой, вписанной в пирамиду, называют такую сферу, которая касается плоскостей всех граней пирамиды, причем точки касания лежат на гранях пирамиды (рис. 4).

Определение 3. Если сфера вписана в пирамиду, то пирамиду называют описанной около сферы.

Если сфера вписана в пирамиду, то она касается граней каждого внутреннего двугранного угла, образованного соседними гранями пирамиды. В соответствии со следствием 1 центр вписанной в пирамиду сферы должен находиться в точке пересечения биссекторных плоскостей всех внутренних двугранных углов, образованных соседними гранями пирамиды.

Если у пирамиды нет точки, в которой пересекаются биссекторные плоскости всех внутренних двугранных углов, образованных соседними гранями пирамиды, то в такую пирамиду нельзя вписать сферу.

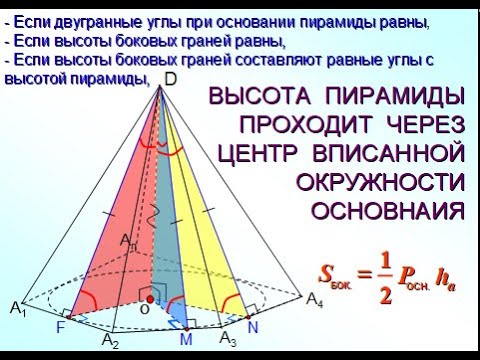
Замечание 1. Для того, чтобы проверить, можно ли в пирамиду вписать сферу, достаточно проверить, существует ли точка пересения биссекторных плоскостей всех внутренних двугранных углов при основании пирамиды. Если такая точка существует, то она будет равноудалена как от основания пирамиды, так и от каждой из боковых граней.

Рассмотрим несколько типов пирамид, в которые можно вписать сферу.

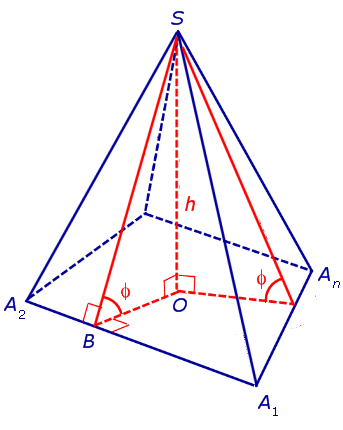
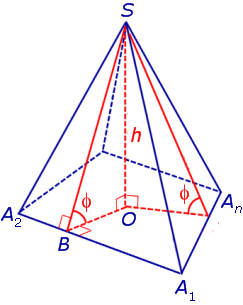
Утверждение 2. Если у пирамиды SA₁A₂ . A_n основание O перпендикуляра, опущенного из вершины S на плоскость основания пирамиды, лежит внутри многоугольника A₁A₂ . A_n , а все боковые грани пирамиды наклонены под одним и тем же углом к плоскости основания пирамиды, то в такую пирамиду можно вписать сферу.

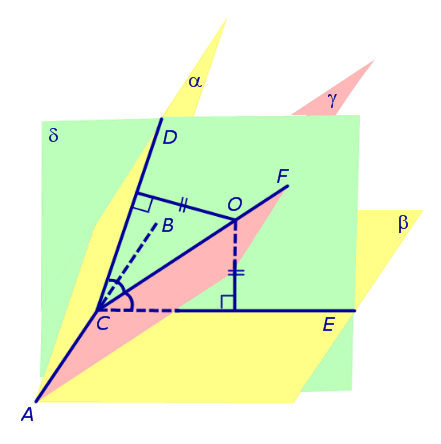
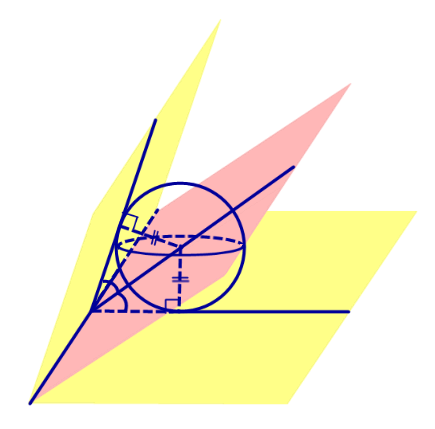
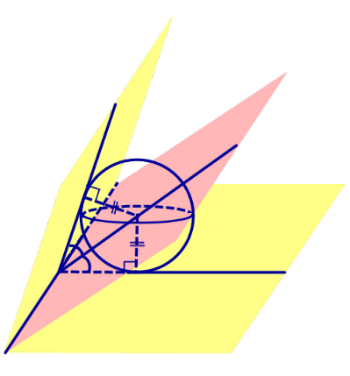
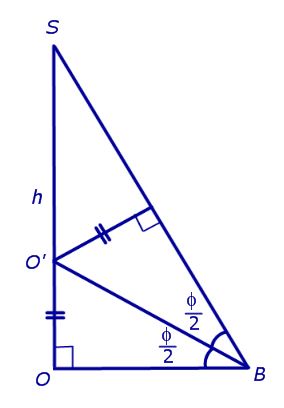
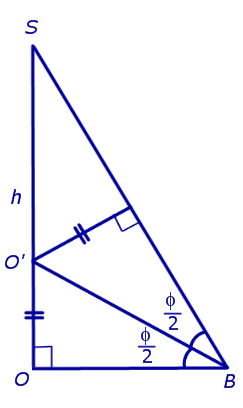
Доказательство. Пусть все боковые грани пирамиды наклонены к плоскости основания под углом φ , а высота пирамиды равна h. Рассмотрим, например, боковую грань SA₁A₂ и проведем в ней высоту SB (рис. 5).

По теореме о трех перпендикулярах отрезок OB перпендикулярен ребру A₁A₂ . Следовательно, угол SBO является линейным углом двугранного угла между боковой гранью SA₁A₂ и плоскостью основания пирамиды и равен φ. Биссекторная плоскость этого двугранного угла пересекает высоту пирамиды в точке O’ (рис. 6).

Катет OB прямоугольного треугольника SOB выражается через высоту пирамиды h и угол φ по формуле

Катет OO’ прямоугольного треугольника OO’B выражается через высоту пирамиды h и угол φ по формуле

Поскольку длина отрезка OO’ не зависит от выбора боковой грани пирамиды, то биссекторные плоскости всех внутренних двугранных углов при основании пирамиды пересекаются в точке O’, которая и является центром вписанной в пирамиду сферы.

Доказательство утверждения 2 завершено.

Поскольку у любой правильной пирамиды все внутренние двугранные углы при основании равны, то справедливо

Следствие 2. В любую правильную пирамиду можно вписать сферу, причем ее радиус R выражается через высоту пирамиды h и внутренний двугранный угол при основании пирамиды φ по формуле

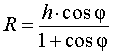(1)

Видео:Как достроить равногранный тетраэдр и найти радиус описанной сферыСкачать

Радиус сферы, вписанной в правильную n — угольную пирамиду

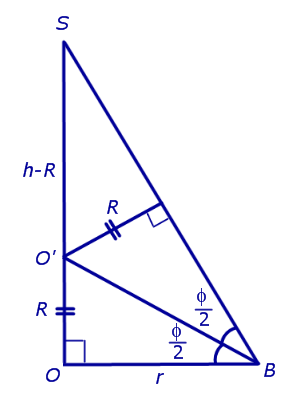
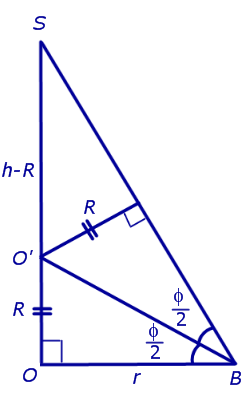
Решение. Рассмотрим правильную n — угольную пирамиду SA₁A₂ . A_n и обозначим символом O’ центр вписанной в пирамиду сферы, а буквой O – центр основания пирамиды. Проведем плоскость через высоту пирамиды SO и апофему SB какой-либо боковой грани (рис. 7).

Буквой R на рисунке 7 обозначен радиус вписанной в пирамиду сферы, буквой r – радиус вписанной в основание пирамиды окружности, а буквой φ – внутренний двугранный угол при основании пирамиды. Из прямоугольного треугольника OSB получаем

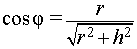(2)

В силу следствия 2 из формул (1) и (2) получаем

из формулы (3) получаем соотношение

Ответ.

Следствие 3. Радиус сферы, вписанной в правильную треугольную пирамиду с высотой h и ребром основания a, равен

Следствие 4. Радиус сферы, вписанной в правильный тетраэдр с ребром a, равен

Следствие 5. Радиус сферы, вписанной в правильную четырехугольную пирамиду с высотой h и ребром основания a, равен

Следствие 6. Радиус сферы, вписанной в правильную шестиугольную пирамиду с высотой h и ребром основания a, равен

Видео:№203. Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярнаяСкачать

Сфера, вписанная в треугольную пирамиду.
Формула для радиуса вписанной сферы

Утверждение 3. В любую треугольную пирамиду можно вписать сферу.

Доказательство. Доказательство этого утверждения напоминает планиметрическое доказательство возможности вписать окружность в произвольный треугольник.

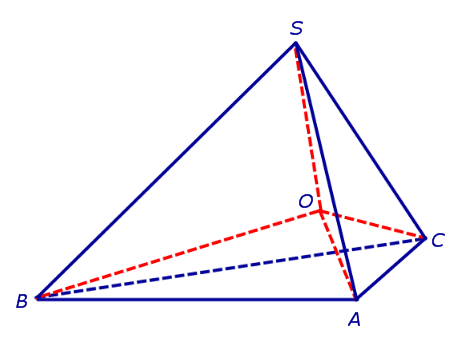
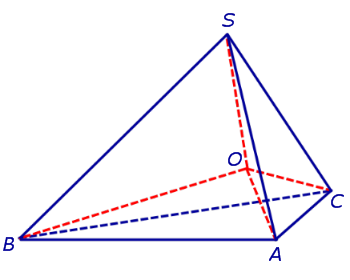
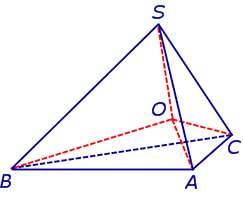
Действительно, пусть SABC – произвольный тетраэдр. Биссекторная плоскость внутреннего двугранного угла с ребром AC и биссекторная плоскость внутреннего двугранного угла с ребром AB пересекаются по некоторой прямой, проходящей через вершину A. Биссекторная плоскость внутреннего двугранного угла в ребром BC пересекает эту прямую в единственной точке O , которая и является центром вписанной сферы (рис. 8).

Получим формулу, позволяющую вычислить радиус вписанной в тетраэдр SABC сферы. Для этого заметим, что объем пирамиды SABC равен сумме объемов пирамид OABC, OSCA, OSAB, OSCB, причем высота каждой из пирамид OABC, OSCA, OSAB, OSCB равна радиусу R вписанной в пирамиду SABC сферы. Если обозначить площади граней тетраэдра SABC символами

а объемы пирамид SABC, OABC, OSCA, OSAB, OSCB – символами

то справедливы следующие равенства:

где символом S_полн обозначена площадь полной поверхности пирамиды SABC.

Замечание 2. Если в пирамиду (необязательно треугольную) можно вписать сферу, то, рассуждая аналогично, можно получить следующую формулу для радиуса вписанной в пирамиду сферы

где символами V_пир и S_полн обозначены объем и площадь полной поверхности пирамиды соответственно.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Центр вписанной окружности в тетраэдре

ТЕТРАЭДР. ВИДЫ ТЕТРАЭДРОВ

Тетраэдр является одним из простейших многогранников, гранями которого являются четыре треугольника. Его можно считать пространственным аналогом треугольника. Рассмотрим свойства треугольников и аналогичные им свойства тетраэдров.
Теорема 1. Биссектрисы треугольника пересекаются в одной точке – центре вписанной окружности.
Теорема 1′. Биссектральные плоскости двугранных углов тетраэдра пересекаются в одной точке – центре вписанной сферы.
Доказательство. Пусть ABCD – тетраэдр. Пересечением биссектральных плоскостей двугранных углов с ребрами AB, AC,и BC (рис. 1) является точка O, равноудаленная от всех граней тетраэдра. Следовательно, эта точка принадлежит биссектральным плоскостям остальных двугранных углов тетраэдра и является центром вписанной сферы.

Теорема 2. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке – центре описанной окружности.
Теорема 2′. Плоскости, проходящие через середины ребер тетраэдра и перпендикулярные этим ребрам, пересекаются в одной точке – центре описанной сферы.
Доказательство. Пусть ABCD – тетраэдр. Пересечением плоскостей, проходящих через середины ребер AD, BD, и CD является точка O, равноудаленная от всех вершин тетраэдра. Следовательно, эта точка принадлежит остальным плоскостям и является центром описанной сферы.
Теорема 2″. Прямые, перпендикулярные граням тетраэдра, и проходящие через центры их описанных окружностей, пересекаются в одной точке – центре описанной сферы.
Доказательство. Каждая такая прямая является геометрическим местом точек, равноудаленных от вершин соответствующей грани тетраэдра. Поэтому центр описанной сферы будет принадлежать всем этим прямым.
Заметим, что не у всякого тетраэдра прямые, проходящие через центры вписанных в грани окружностей и перпендикулярные этим граням, пересекаются в одной точке. Ответ на то, когда это происходит, дает следующая теорема.
Теорема 2»’. У тетраэдра существует сфера, касающаяся всех его ребер, тогда и только тогда, когда суммы противоположных ребер этого тетраэдра равны.
Доказательство. Пусть у тетраэдра ABCD существует сфера, касающаяся его ребер. Обозначим через a, b, c и d расстояния от соответствующих вершин тетраэдра до точек касания. Тогда AB = a + b, CD = c + d. Следовательно, AB + CD = a + b + c + d. Аналогично, AC + BD = a + b + c + d, AD + BC = a + b + c + d. Таким образом, суммы противоположных ребер тетраэдра равны.
Обратно. Предположим, что суммы противоположных ребер тетраэдра ABCD равны. Впишем в треугольник ABC окружность. Обозначим через X точку касания этой окружности стороны AB (рис. 2) .

Тогда AX = (AB + AC – BC):2. Так как AC – BC = AD – BD, то AX = (AB + AD – BD):2. Следовательно, точка X является точкой касания окружности, вписанной в треугольник ABD . Через центры этих двух окружностей проведем перпендикуляры. Они лежат в одной плоскости, проходящей через X и перпендикулярной AB. Точка O их пересечения будет равноудалена от сторон треугольников ABC и ABD. Таким образом, любые два перпендикуляра, проходящие через центры окружностей, вписанных в грани тетраэдра, пересекаются. Из этого следует, что или они лежат в одной плоскости, или пересекаются в одной точке. Поскольку они не лежат в одной плоскости, то значит, они пересекаются в одной точке O , равноудаленной от всех ребер тетраэдра, т.е. O – центр сферы, касающейся всех ребер данного тетраэдра.
Теорема 3. Медианы треугольника пересекаются в одной точке, называемой центроидом треугольника и делятся в этой точке в отношениии 2 : 1.
Теорема 3′. Отрезки, соединяющие вершины тетраэдра с точками пересечения медиан противоположных граней, пересекаются в одной точке – центроиде тетраэдра и делятся в этой точке в отношении 3 : 1, считая от вершины.
Доказательство. Пусть ABCD – тетраэдр, O – точка пересечения медиан треугольника ABC, P – точка пересечения медиан треугольника BCD, R – точка пересечения отрезков DO и AP (рис. 3) .

Рассмотрим треугольник AQD. Точки O и P делят соответствующие стороны в отношении 2 : 1. Покажем, что точка R делит DO и AP в отношении 3 : 1. В треугольнике APQ проведем OS параллельно AP. Она разделит отрезок PQ в отношении 2 : 1. Если отрезок SQ принять за единицу, то отрезок DP будет равен 6. Отрезки DR и RQ относятся также как DP и PS, т.е. DR : RQ = 6 : 2 = 3 : 1. Аналогичным образом доказывается, что точка R делит отрезок AP в отношении 3 : 1. Отрезки, соединяющие вершины B и C с точками пересечения медиан противоположных граней также будут делить отрезок DO в отношении 3 : 1 и, следовательно, будут проходить через точку O . Что и требовалось доказать.
Теорема 4. Отрезки, соединяющие середины противоположных ребер тетраэдр, пересекаются в одной точке – центроиде.
Доказательство. Достаточно заметить, что в предыдущем доказательстве медиана треугольника AQD, проведенная из вершины Q, проходит через центроид O .
Теорема 5. Для цетроида O треугольника ABC имеет место равенство .
Теорема 5′. Для цетроида O тетраэдра ABCD имеет место равенство .
Теорема 6. Пусть a произвольная прямая, проходящая через центроид треугольника ABC. Будем считать одну из полуплоскостей, на которые эта прямая разбивает плоскость, положительной, а другую отрицательной. Тогда сумма расстояний от вершин треугольника до прямой a, взятых со знаком + или – в зависимости от того, какой полуплоскости принадлежит вершина, равна нулю.
Теорема 6′. Пусть произвольная плоскость, проходящая через центроид тетраэдра ABCD. Будем считать одно из полупространств, на которые эта плоскость разбивает пространство, положительным, а другое отрицательным. Тогда сумма расстояний от вершин тетраэдра до плоскости , взятых со знаком + или – в зависимости от того, какому полупространству принадлежит вершина, равна нулю.
Теорема 7. Пусть a произвольная прямая. Будем считать одну из полуплоскостей, на которые эта прямая разбивает плоскость, положительной, а другую отрицательной. Тогда сумма расстояний от вершин треугольника до прямой a, взятых со знаком + или – в зависимости от того, какой полуплоскости принадлежит вершина, равна утроенному расстоянию от центроида треугольника до прямой a .
Теорема 7′. Пусть a произвольная плоскость. Будем считать одно из полупространств, на которые эта плоскость разбивает пространство, положительным, а другое отрицательным. Тогда сумма расстояний от вершин тетраэдра до плоскости a , взятых со знаком + или – в зависимости от того, какому полупространству принадлежит вершина, равна учетверенному расстоянию от центроида тетраэдра до данной плоскости.
Теорема 8′ (Менелая). Пусть на ребрах AB, BC, CD и AD тетраэдра ABCD взяты соответственно точки A ₁ , B ₁ , C ₁ и D ₁ . Для того чтобы эти точки лежали в одной плоскости, необходимо и достаточно, чтобы выполнялось равенство

Доказательство. Пусть точки A ₁ , B ₁ , C ₁ и D ₁ лежат в одной плоскости (рис. 4). Опустим из вершин тетраэдра перпендикуляры AA ’ , BB ’ , CC ’ , DD ’ на эту плоскость. Тогда AA ₁ : A ₁ B = AA ’ : BB ’ , BB ₁ : B ₁ C = BB ’ : CC ’ , CC ₁ : C ₁ D = CC ’ : DD ’ , DD ₁ : D ₁ A = DD ’ : AA ’ . Откуда и следует требуемое равенство.

Обратно, пусть выполняется указанное равенство. Через точки A ₁ , B ₁ , C ₁ проведем плоскость. Она пересечет ребро AD в некоторой точке D ’ . Для точек A ₁ , B ₁ , C ₁ и D ’ также выполняется указанное равенство. Из этого следует, что DD ₁ : D ₁ A = DD ’ : D ’ A и, значит, D ₁ и D ’ совпадают, т.е. A ₁ , B ₁ , C ₁ и D ₁ лежат в одной плоскости.

Теорема 9′ (Чевы). Пусть на ребрах AB, BC, CD и AD тетраэдра ABCD взяты соответственно точки A ₁ , B ₁ , C ₁ и D ₁. Плоскости ABC ₁ , BCD ₁ , CDA ₁ и DAB ₁ пересекаются в одной точке тогда и только тогда, когда

Доказательство. По предыдущей теореме выполнимость указанного равенства равносильна тому, что точки A ₁ , B ₁ , C ₁ и D ₁ лежат в одной плоскости. При этом точка пересечения этих плоскостей является точкой пересечения диагоналей четырехугольника A ₁ B ₁ C ₁ D ₁ .

Рассмотрим теперь некоторые специальные тетраэдры.
Равногранным тетраэдром называется тетраэдр, у которого все грани равны.
Теорема 10. Для любого остроугольного треугольника существует равногранный тетраэдр, грани которого равны данному треугольнику.
Доказательство. Пусть ABC – произвольный остроугольный треугольник. Через его вершины проведем прямые, параллельные противоположным сторонам (рис. 5).

Они образуют треугольник A ₁ B ₁ C ₁ , разбитый на четыре треугольника, равных исходному. Ясно, что A ₁ B ₁ C ₁ представляет собой развертку равногранного тетраэдра.
Теорема 11. Тетраэдр является равногранным тогда и только тогда, когда у него центры вписанной и описанной сфер совпадают.
Доказательство. Пусть в тетраэдре ABCD центрами вписанной и описанной сфер является точка O . P и Q – и точки касания вписанной сферы граней ABC и BCD (рис.6) . Заметим, что P и Q являются центрами окружностей, описанных около треугольников ABC и BCD соответственно. Из этого, в частности, следует, что треугольник ABC – остроугольный. Кроме того, треугольники BP C и BQ C равны. Углы BAC и BDC равны половинам углов BP C и BQ C , и следовательно также равны. Таким образом, плоские углы при вершине D равны углам треугольника ABC. Значит, в сумме они составляют 180 0 . Аналогично, плоские углы при остальных вершинах тетраэдра в сумме составляют 180 0 . Поэтому развертка этого тетраэдра имеет вид, указанный в теореме 1. Следовательно, тетраэдр равногранный.

Покажем обратное, пусть ABCD – равногранный тетраэдр, O – цетр описанной сферы. Тогда плоскости граней пересекают описанную сферу по окружностям одинакового радиуса. Следовательно, расстояния от точки O до граней тетраэдра равны и, значит O – центр вписанной сферы.
Прямоугольным тетраэдром называется тетраэдр, у которого все плоские углы при какой-нибудь вершине прямые.
Теорема 12. Основанием высоты прямоугольного тетраэдра, проведенной из вершины с прямыми плоскими углами, является точка пересечения высот противоположной грани.
Теорема 13. (Пифагора) Квадрат площади грани прямоугольного тетраэдра, лежащей против вершины с прямыми плоскими углами, равен сумме квадратов площадей остальных граней этого тетраэдра.
Доказательство. Пусть ABCD – прямоугольный тетраэдр (рис. 7). Плоские углы при вершине D прямые. Можно было бы обозначить ребра, выходящие из вершины D через a, b, c, а затем воспользоваться формулой Герона для нахождения площади треугольника ABC .

Мы рассмотрим другой способ. Имеем S _ADB = S _ABC cos ; S _ACD = S _ABC cos ; S _BCD = S _ABC cos , где , , — соответствующие двугранные углы, равные углам C DO, BDO и A DO . Таким образом, cos , cos , cos составляют координаты единичного вектора, поэтому cos 2 + cos 2 + cos 2 = 1. Значит , S 2 _ABC = S 2 _ABD + S 2 _BCD + S 2 _ACD . Что и требовалось доказать.
Ортогональным называется тетраэдр, у которого противоположные ребра попарно перпендикулярны.
Ортоцентрическим называется тетраэдр, у которого высоты или их продолжения пересекаются в одной точке – ортоцентре третаэдра.
Теорема 14. Тетраэдр является ортогональным тогда и только тогда, когда отрезки, соединяющие середины противоположных ребер, равны.
Доказательство. Пусть ABCD – тетраэдр. A ₁ , B ₁, C ₁, D ₁ – середины двух пар противоположных ребер (рис. 8).

Тогда A ₁ B ₁ D ₁ C ₁ – параллелограмм. Его диагонали равны тогда и только тогда, когда он – прямоугольник, т.е. AC BD .
Теорема 2. Тетраэдр является ортогональным тогда и только тогда, когда он является ортоцентрическим.
Доказательство. Пусть ABCD – ортогональный тетраэдр (рис. 9). DD ₂ – высота, опущенная из вершины D. Плоскость CDD ₂ перпендикулярна AB и, следовательно, DC ₁ и CC ₁ – высоты треугольников ABC и ABD. Высоты DD ₂ и CC ₂ треугольника C ₁ CD пересекаются.

Таким образом, произвольные пары высот тетраэдра пересекаются в одной точке. Но попарно пересекающиеся прямые или лежат в одной плоскости, или пересекаются в одной точке. В нашем случае прямые не лежат в одной плоскости и, следовательно, пересекаются в одной точке O .
Обратно, пусть высоты тетраэдра ABCD пересекаются в одной точке O. Тогда DD ₂ ABC и, следовательно, DD ₂ ABC . Аналогично, CC ₂ ABD и, следовательно, CC ₂ AB . Таким образом, AB перпендикулярна плоскости COD и, следовательно, AB CD. Аналогично показывается перпендикулярность остальных противоположных ребер.
Теорема 3. Тетраэдр является ортогональным тогда и только тогда, когда одна из его высот проходит через ортоцентр соответствующей грани.
Доказательство. Необходимость вытекает из Теоремы 2. Покажем достаточность. Пусть D ₂ – ортоцентр грани ABC, DD ₂ – высота тетраэдра ABCD. Тогда BC перпендикулярна плоскости AA ₁ D и, следовательно, BC перпендикулярна AD. Аналогично показывается перпендикулярность остальных противоположных ребер.
Теорема 4. В ортогональном тетраэдре окружности 9-ти точек всех граней лежат на одной сфере (сфера 24 точек).
Доказательство. Рассмотрим сферу с центром в центроиде тетраэдра и диаметром, равным отрезкам, соединяющим середины противоположных ребер. Эта сфера проходит через середины всех ребер тетраэдра и, следовательно, содержит окружности 9 точек всех граней.

Литература
1. Адамар Ж. Элементарная геометрия. Часть II. Стереометрия. – М.: Учпедгиз, 1938.
2. Перепелкин Д.И. Курс элементарной геометрии. Часть II. Геометрия в пространстве. – М.-Л.: Гостехиздат, 1949.
3. В.В.Прасолов, И.Ф.Шарыгин. Задачи по стереометрии. – М.: Наука, 1989.
4. Д.О.Шклярский, Н.Н.Ченцов, И.М.Яглом. Избранные задачи и теоремы элементарной математики. Часть 3. – М.: Государственное издательство технико-теоретической литературы, 1954.

Видео:Пирамиды, в которых высота проходит через центр вписанной в основание окружностиСкачать

Тетраэдр.

Тетраэдр — это частный случай правильной треугольной пирамиды.

Тетраэдр — правильный многогранник (четырёхгранный), имеющий 4 грани, они, в свою очередь, оказываются правильными треугольниками. У тетраэдра 4 вершины, к каждой из них сходится 3 ребра. Общее количество ребер у тетраэдра 6.

Медиана тетраэдра — это отрезок, который соединяет вершину тетраэдра и точку пересечения медиан противоположной грани (медиан равностороннего треугольника, который противолежит вершине).

Бимедиана тетраэдра — это отрезок, который соединяет середины рёбер, что скрещиваются (соединяет середины сторон треугольника, который есть одной из граней тетраэдра).

Высота тетраэдра — это отрезок, который соединяет вершину и точку противоположной грани и перпендикулярен этой грани (т.е. это высота, проведенная от всякой грани, кроме того, совпадает с центром описанной окружности).

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Свойства тетраэдра.

Параллельные плоскости, которые проходят через пары рёбер тетраэдра, что скрещиваются, и определяют описанный параллелепипед около тетраэдра.

Плоскость, которая проходит сквозь середины 2-х рёбер тетраэдра, что скрещиваются, и делит его на 2 части, одинаковые по объему.

Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, если считать от вершины. Она же делит бимедианы на две равные части.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Типы тетраэдров.

Правильный тетраэдр — это такая правильная треугольная пирамида, каждая из граней которой оказывается равносторонним треугольником.

У правильного тетраэдра каждый двугранный угол при рёбрах и каждый трёхгранный угол при вершинах имеют одинаковую величину.

Тетраэдр состоит из 4 граней, 4 вершин и 6 ребер.

Правильный тетраэдр — это один из 5-ти правильных многогранников.

Кроме правильного тетраэдра, заслуживают внимания такие типы тетраэдров:

— Равногранный тетраэдр, у него каждая грань представляет собой треугольник. Все грани-треугольники такого тетраэдра равны.

— Ортоцентрический тетраэдр, у него каждая высота, опущенная из вершин на противоположную грань, пересекается с остальными в одной точке.

— Прямоугольный тетраэдр, у него каждое ребро, прилежащее к одной из вершин, перпендикулярно другим ребрам, прилежащим к этой же вершине.

— Каркасный тетраэдр — тетраэдр, который таким условиям:

есть сфера, которая касается каждого ребра,
суммы длин ребер, что скрещиваются равны,
суммы двугранных углов при противоположных ребрах равны,
окружности, которые вписаны в грани, попарно касаются,
каждый четырехугольник, образующийся на развертке тетраэдра, — описанный,
перпендикуляры, поставленные к граням из центров окружностей, в них вписанных, пересекаются в одной точке.

— Соразмерный тетраэдр, бивысоты у него одинаковы.

— Инцентрический тетраэдр, у него отрезки, которые соединяют вершины тетраэдра с центрами окружностей, которые вписаны в противоположные грани, пересекаются в одной точке.

Видео:Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Формулы для определения элементов тетраэдра.

Высота тетраэдра:

где h — высота тетраэдра, a — ребро тетраэдра.

Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.