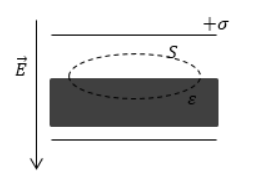
Вектор электрического смещения в конденсаторе (7 видео)

3.4. Вектор электрического смещения

Разобравшись с поведением диэлектрика на микроскопическом уровне, вернемся к плоскому конденсатору, изображенному на рис. 3.3. Откуда же взялись поляризационные заряды на поверхности диэлектрической пластины между обкладками?

Теперь мы знаем, что во внешнем поле, создаваемом обкладками, единица объема диэлектрика приобретает дипольный момент Р. Скажем, положительные заряды смещаются по направлению поля (вверх на рис. 3.3), а отрицательные — вниз. При полной однородности поля и диэлектрика объемные нескомпенсированные заряды внутри диэлектрика не появляются. Но такой сдвиг приводит к возникновению нескомпенсированных зарядов на поверхности диэлектрической пластины. Дипольный момент пластины равен VР, где V = Sd — ее объем. С другой стороны, полный поверхностный заряд на пластине равен

а расстояние между центрами положительных и отрицательных зарядов равно d (см. рис. 3.3). Поэтому дипольный момент пластины можно также записать как

Сравнивая эти два выражения, находим связь поверхностной плотности поляризационных зарядов с вектором поляризации

Напряженность Е суммарного поля внутри диэлектрика меньше напряженности поля E₀, создаваемого обкладками. Именно поле Е действует на молекулы диэлектрика, именно его они «чувствуют», и потому для него справедливо соотношение (3.22)

Используя связь (3.3) напряженности поля Е ‘ поляризационных зарядов с суммарным полем Е

мы находим связь между диэлектрической проницаемостью и диэлектрической восприимчивостью

В общем случае вектор поляризации Р не параллелен вектору напряженности суммарного поля Е: в анизотропных диэлектриках вектор поляризации может поворачиваться относительно напряженности поля. Однако всегда мы можем записать соотношение

называется вектором электрического смещения (вектором электрической индукции).

В частном случае линейной зависимости поляризации от напряженности поля

вектор электрического смещения равен

где — диэлектрическая проницаемость среды. Соотношение

имеет место для изотропных диэлектриков. В общем случае вектор D не параллелен Е. Поле вектора D можно графически изобразить линиями электрического смещения, которые определяются так же, как и линии напряженности электрического поля (рис 3.23 и 3.24).

Рис. 3.23. Условия на плоской границе двух диэлектриков для напряженности и электрического смещения

Рис. 3.24. Линии напряженности и электрического смещения электрического поля
от точечного заряда, расположенного на границе раздела двух диэлектриков

В СИ единицей измерения электрического смещения является:

Содержание

Вектор электрической индукции
Вектор индукции
Связь вектора напряженности и вектора электрического смещения
Поляризация. Электрическое смещение в диэлектрике
Заключение
💥 Видео

Видео:45. Электрическое смещениеСкачать

Вектор электрической индукции

Вектором электрической индукции (электрического смещения) D → называют физическую величину, определяемую по системе С И :

D → = ε 0 E → + P → , где ε 0 — электрическая постоянная, E → — вектор напряженности, P → — вектор поляризации.

Вектор электрического смещения в СНС определяется как:

Видео:Урок 383. Вихревое электрическое поле. Ток смещенияСкачать

Вектор индукции

Значение вектора D → не является только полевым, потому как он учитывает поляризованность среды. Имеется связь с объемной плотностью заряда, выражаемая соотношением:

По уравнению d i v D → = ρ видно, что для D → единственным источником будут являться свободные заряды, на которых данный вектор начинается и заканчивается. В точках с отсутствующими свободными зарядами вектор электрической индукции является непрерывным. Изменения напряженности поля, вызванные наличием связанных зарядов, учитываются в самом векторе D → .

Видео:44. Электрическое поле в диэлектрике. Вектор поляризованностиСкачать

Связь вектора напряженности и вектора электрического смещения

При наличии изотропной среды запись связи вектора напряженности и вектора электрического смещения запишется как:

D → = ε 0 E → + ε 0 χ E → = ε 0 + ε 0 χ E → = ε ε 0 E → .

Где ε – диэлектическая проницаемость среды.

Наличие D → способствует облегчению анализа поля при наличии диэлектрика. Используя теорему Остроградского-Гаусса в интегральном виде с диэлектриком, фиксируется как:

Проходя через границу разделов двух диэлектриков для нормальной составляющей, вектор D → может быть записан:

D 2 n — D 1 n = σ

n 2 → D 2 → — D 1 → = σ ,

где σ – поверхностная плотность распределения зарядов на границе диэлектриков, n 2 → — нормаль, проведенная в сторону второй среды.

Формула тангенциальной составляющей:

D 2 τ = ε 2 ε 1 D 1 τ .

Единица вектора электрической индукции измеряется в системе С И как К л м 2 .

Поле вектора D → изображается при помощи линий электрического смещения.

Определение направления и густоты идет аналогично линиям вектора напряженности. Но линии вектора электрической индукции начинаются и заканчиваются только на свободных зарядах.

Имеются пластины плоского конденсатора с зарядом q . Произойдет ли изменение вектора электрической индукции при заполненном воздухом пространстве между пластинами и диэлектрика с диэлектрической проницаемостью ε ≠ ε υ o z d .

Поле конденсатора в первом случае характеризовалось вектором смещения ε v o z d = 1 , то есть D 1 → = ε v o z d ε 0 E 1 → = ε 0 E 1 → .

Необходимо заполнить пространство между пластинами конденсатора однородным и изотропным диэлектриком. При наличии поля в конденсаторе диэлектрик поляризуется. Тогда начинают появляться связанные заряды с плотностью σ s υ на его поверхности. Создается дополнительное поле с напряженностью:

Векторы полей E → ‘ и E 1 → имеют противоположные направления, причем:

Запись результирующего поля с диэлектриком примет вид:

E = E 1 — E ‘ = σ ε 0 — σ s υ ε 0 = 1 ε 0 σ — σ s υ .

Формула плотности связанных зарядов:

Произведем подстановку σ s υ = χ ε 0 E в E = E 1 — E ‘ = σ ε 0 — σ s υ ε 0 = 1 ε 0 σ — σ s υ , тогда:

Далее выражаем из ( 1 . 6 ) напряженность поля Е . Формула принимает вид:

E = E 1 1 + χ = E 1 ε .

Отсюда следует, что значение вектора электрической индукции в диэлектрике равняется:

D = ε ε 0 E 1 ε = ε 0 E 1 = D 1 .

Ответ: вектор электрической индукции не изменяется.

Была внесена пластина из диэлектрика с диэлектрической проницаемостью ε без свободных зарядов в зазор между разноименными заряженными пластинами. На рисунке 1 показана при помощи штриховой линии замкнутая поверхность. Определить поток электрической индукции Φ D через эту поверхность.

Рисунок 1 . Замкнутая поверхность

Формула записи потока вектора электрического смещения Φ D через замкнутую поверхность S :

Φ D = ∫ S D → · d S → .

Используя теорему Остроградского-Гаусса, можно сказать, что Φ D равняется суммарному свободному заряду, находящемуся внутри заданной поверхности. Из условия видно отсутствие свободных зарядов в диэлектрике и в имеющемся пространстве между пластинами конденсатора, а поток вектора индукции равняется нулю.

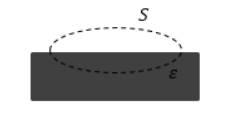
Изображена замкнутая поверхность S , проходящая с захватом части пластины изотропного диэлектрика на рисунке 2 . Поток вектора электрической индукции через нее равняется нулю, а поток вектора напряженности > 0 . Какой вывод можно сделать из данной задачи?

Рисунок 2 . Замкнутая поверхность с захватом части пластины изотропного диэлектрика

Из условия имеем, что поток вектора электрического смещения Φ D через замкнутую поверхность равняется нулю, то есть:

Если использовать теорему Остроградского-Гаусса, то значение Φ D – это суммарный свободный заряд, находящийся внутри заданной поверхности. Следует, что внутри такой поверхности отсутствуют свободные заряды:

Φ D = ∫ S D → · d S → = Q = 0 .

Имеем, что поток вектора напряженности не равен нулю, но он считается как сумма свободных и связанных зарядов. Отсюда вывод – диэлектрик содержит связанный заряды.

Ответ: свободные заряды отсутствуют, а связанные есть, причем с положительной их суммой.

Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Поляризация. Электрическое смещение в диэлектрике

Публикации по материалам Д. Джанколи. «Физика в двух томах» 1984 г. Том 2.

Прямоугольная диэлектрическая пластина между заряженными обкладками плоского конденсатора на рис. 25.9 обладает дипольным моментом Q_инд/l, где l — толщина диэлектрика, а Q_инд — заряд, наведенный на поверхности диэлектрика. Для характеристики диэлектрика можно ввести новую величину — вектор поляризации P, дипольный момент единицы объема. Для прямоугольной диэлектрической пластины площадью A и толщиной l

Таким образом, величина вектора поляризации в данном случае равна поверхностной плотности наведенного на диэлектрике заряда (в более сложных случаях величина ? равна составляющей P, перпендикулярной поверхности.)

Вектор поляризации направлен от поверхности с отрицательным зарядом с одной стороны диэлектрика к поверхности с положительным зарядом на противоположной стороне (подобно вектору дипольного момента), как показано на рис. 25.9. Для изображенной на этом рисунке штриховой линией поверхности можно написать

Поскольку поляризация равна P = 0 в проводнике и параллельна торцам поверхности интегрирования. Формула (25.14) справедлива и в общем случае, и ее можно объединить с (25.12):

Это еще один способ записи теоремы гаусса при наличии диэлектрика [см. также (25.12) и (25.13)], представляющий собой общий результат.
Теорему Гаусса можно сформулировать, введя вектор электрического смещения D, который определяется как

для диэлектрика, находящегося между пластинами плоского конденсатора (рис. 25.9), это соотношение дает

где Q — свободный заряд.

Векторы E, D и P допускают наглядное толкование. Напряженность электрического поля E создается всеми зарядами, свободными и связанными, как это следует из (25.12). поляризация P, как видно из формулы (25.14), связана только с индуцированным связанным зарядом. Электрическое смещение D обусловлено только свободным зарядом, как следует из (25.17) и (25.18).

И все же основной характеристикой электрического поля остается вектор напряженности электрического поля E. векторы P и D служат полезными дополнительными характеристиками для более глубокого анализа, однако мы не будем часто пользоваться ими.

Видео:Билет №31 "Ток смещения"Скачать

Заключение

Конденсатор -это устройство, аккумулирующее электрический заряд; он состоит из двух изолированных проводников (обкладок). проводники обычно несут на себе равные по величине и противоположные по знаку заряды, и отношение величины этого заряда к разности потенциалов между проводниками называется емкостью C: Q = CV.
Ёмкость плоского конденсатора пропорциональна площади каждой из обкладок и обратно пропорциональна расстоянию между ними. Пространство между обкладками обычно заполнено веществом, не проводящим электричества (воздухом, бумагой, пластмассой); такие вещества называются диэлектриками. Ёмкость конденсатора пропорциональна характеристике диэлектрика, которая называется относительной диэлектрической проницаемостью K (и которая для воздуха практически равна 1).

Если два или более конденсаторов соединены параллельно, то их общая емкость с равна сумме емкостей отдельных конденсаторов. При последовательном соединении конденсаторов величина, обратная их общей емкости C, равна сумме величин, обратных емкостям отдельных конденсаторов.

Энергия, накопленная заряженным конденсатором, равна 1/2(QV)= 1/2(CV 2 ) = 1/2(Q 2 /C) эту энергию можно рассматривать как энергию электрического поля, заключенного между обкладками конденсатора. плотность энергии (энергия единицы объема) электрического поля E в вакууме равна 1/2(?₀E 2 ),
а в диэлектрике 1/2(K?₀E 2 ) = 1/2(?E 2 ),
где ? = K?₀ называют абсолютной диэлектрической проницаемостью вещества.