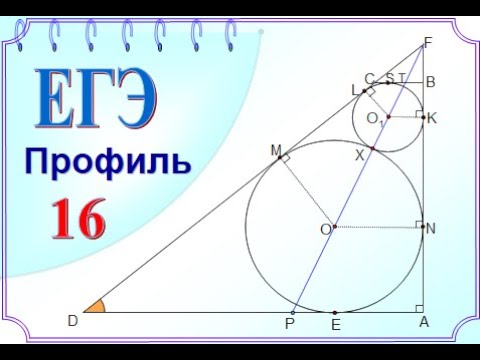
Общие касательные к двум окружностям
 Взаимное расположение двух окружностей Взаимное расположение двух окружностей |
 Общие касательные к двум окружностям Общие касательные к двум окружностям |
 Формулы для длин общих касательных и общей хорды Формулы для длин общих касательных и общей хорды |
 Доказательства формул для длин общих касательных и общей хорды Доказательства формул для длин общих касательных и общей хорды |
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- Две окружности пересекаются в точках a b и общая касательная
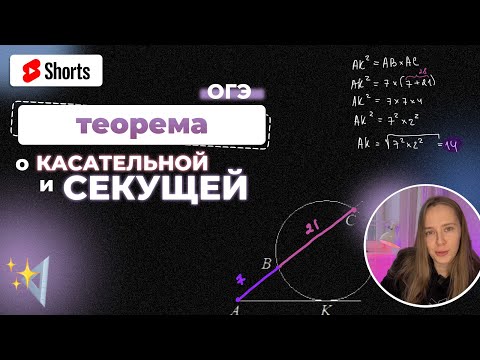
- Касательная к окружности
- Касательная к окружности, секущая и хорда — в чем разница
- Свойства касательной к окружности
- Задача
- Задача 1
- Задача 2
- Задача 1
- Задача 2
- Задача 1
- Задача 2
- 💡 Видео
Видео:Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  | |
| Каждая из окружностей лежит вне другой |  | |
| Внешнее касание двух окружностей |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  |  |
| Каждая из окружностей лежит вне другой | ||
 | ||
| Внешнее касание двух окружностей | ||
 | ||
| Внутреннее касание двух окружностей | ||
 | ||
| Окружности пересекаются в двух точках | ||
 | ||
 | ||
| Каждая из окружностей лежит вне другой | ||
 Расстояние между центрами окружностей больше суммы их радиусов | ||
| Внешнее касание двух окружностей | ||
 Расстояние между центрами окружностей равно сумме их радиусов | ||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||
 Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой | ||
| Внутренняя касательная к двум окружностям |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  | |
| Внешнее касание двух окружностей |  | |
 | ||
 | ||
| Внешняя касательная к двум окружностям | |
 | |
| Внутренняя касательная к двум окружностям | |
 | |
| Внутреннее касание двух окружностей | |
 | |
| Окружности пересекаются в двух точках | |
 | |
| Внешнее касание двух окружностей | |
 | |
 | |
| Каждая из окружностей лежит вне другой | |
 | |
| Внешняя касательная к двум окружностям | ||||||||||||||||||||||||||||
| Внутренняя касательная к двум окружностям | ||||||||||||||||||||||||||||
| Внутреннее касание двух окружностей | ||||||||||||||||||||||||||||
| Окружности пересекаются в двух точках | ||||||||||||||||||||||||||||
| Внешнее касание двух окружностей | ||||||||||||||||||||||||||||
| Каждая из окружностей лежит вне другой | ||||||||||||||||||||||||||||
| Фигура | Рисунок | Формула | |||||||||||||||||||
| Внешняя касательная к двум окружностям |  | ||||||||||||||||||||
| Внутренняя касательная к двум окружностям |  | ||||||||||||||||||||
| Общая хорда двух пересекающихся окружностей |  | ||||||||||||||||||||
| Внешняя касательная к двум окружностям | |||||||||||
 | |||||||||||
| Внутренняя касательная к двум окружностям | |||||||||||
 | |||||||||||
| Общая хорда двух пересекающихся окружностей | |||||||||||
 | |||||||||||
| Внешняя касательная к двум окружностям | |||||||
| Внутренняя касательная к двум окружностям | |||||||
| Общая хорда двух пересекающихся окружностей | |||||||
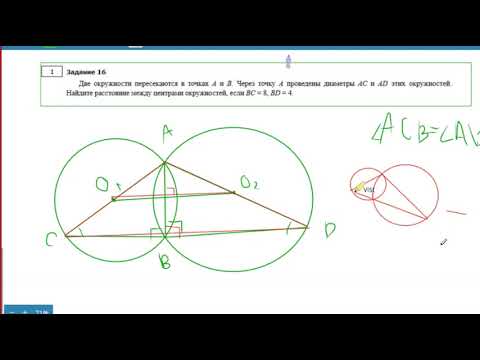
 Длина общей хорды двух окружностей вычисляется по формуле Видео:Геометрия Две окружности пересекаются в точках A и B. Через точку A проведены диаметры AC и AD этихСкачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:Касательные к окружности пересекаются в точке. Теорема и решение задач. Геометрия 7-8 классСкачать  Две окружности пересекаются в точках a b и общая касательнаяДве окружности касаются внешним образом в точке A, через которую проведена их общая касательная, на которой отмечена точка B. Через точку B проведены две прямые: одна пересекает первую окружность в точках K и L (точка K находится между B и L), а другая — вторую окружность в точках M и N (точка M находится между B и N). Прямые KN и LM пересекаются в точке P. а) Докажите, что точки K, L, M, N лежат на одной окружности. б) Найдите отношение площадей треугольников KLP и MNP, если BL = 9, BM = 5, AB = 6. а) Заметим, что по теореме о квадрате касательной Значит, треугольники BKM и BNL подобны по двум пропорциональным сторонам и углу между ними, причем б) Треугольники KPL и MPN подобны по двум углам, поэтому отношение их площадей равно квадрату коэффициента подобия, то есть Ответ:
|