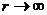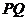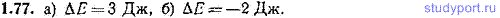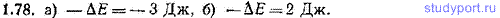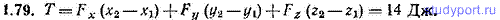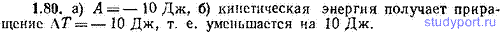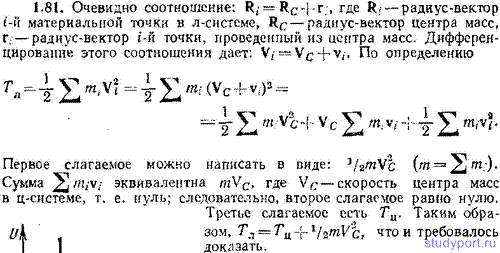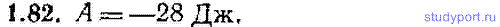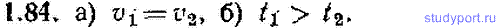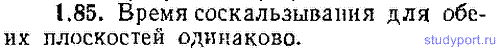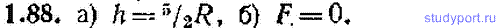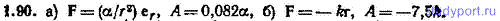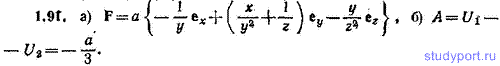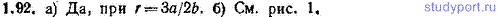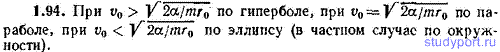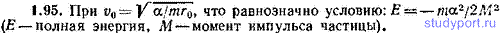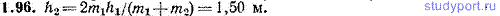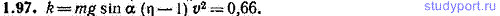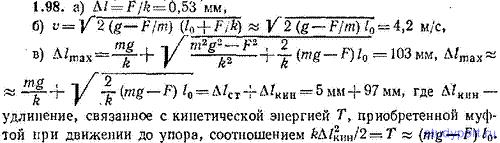12.1. Сохранение момента импульса в центральном поле.
Сила называется центральной, если для всех точек поля она направлена к одной и той же точке (или от одной и той же точки) и зависит только от расстояния до этой точки, называемой центром сил, или силовым центром.
Уже из определения следует, что центральные силы консервативны.
Итак, центральная сила:
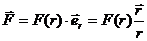
Поскольку эта сила консервативна, то можно ввести потенциальную энергию:
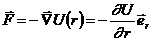
При движении в центральном поле момент силы равен нулю, т.к. угол между векторами в векторном произведении равен нулю:
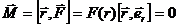
Тогда из уравнения моментов (11.5) получаем, что момент импульса есть постоянная величина.
При движении частицы в центральном поле полный момент импульса сохраняется, несмотря на то, что система (одна частица) не является замкнутой.

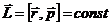
Так как 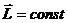
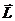
перпендикулярен к векторам 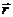
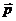
происходит в плоскости, перпендикулярной к 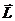
что частица в поле центральных сил движется по плоской орбите.
Если ось 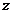
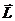
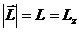
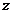
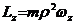
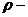
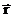
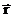
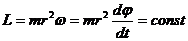
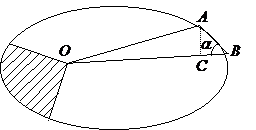 |
Пусть частица движется в в поле центральных сил по плоской траектории, представляющей собой замкнутую кривую.
Площадь 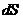
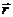
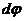
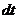
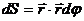
Выберем за начало отсчета точку О и найдем площадь сектора 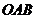
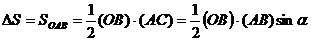
Здесь 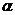
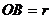
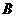
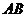
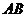
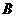
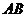
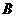
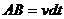
Тогда можем записать
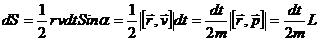
Вводя понятие секториальной скорости как площади, описываемой радиусом-вектором 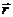
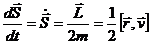
Т.о., мы получили математическое выражение 2-го закона Кеплера, устанавливающего постоянство секториальной скорости планеты 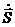
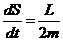
Этому закону подчиняется, например, движение планет по эллиптическим орбитам.
Примечание: Закон сохранения момента импульса частицы, движущейся в центральном поле иногда
называют “интегралом площадей”.
Итак, свойства движения частицы в центральном поле:
1) движение плоское, плоскость проходит через точку 0, определенный относительно которой момент импульса частицы сохраняется.
2) секториальная скорость постоянна (II закон Кеплера).
12.2. Закон сохранения энергии в центральном поле.
Центральные силы консервативны, следовательно, полная энергия частицы в системе «силовой центр – частица» (замкнутая система) сохраняется.
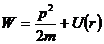
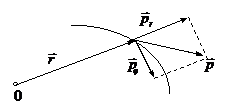
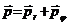
В полярных координатах выражения для момента импульса 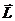
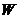
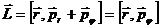
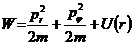
В выражении (12.10) 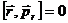
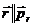
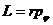
т.к. траектория частицы плоская и 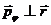
Если, воспользовавшись (12.10), исключить из уравнения (12.11) азимутальную составляющую импульса частицы 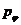
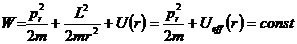
Примечание. Величину 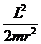
Уравнение (12.12) содержит только одну неизвестную – радиальную компоненту импульса 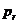
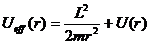
Т.о., можно сказать, что задача о движении частицы в центральном поле сводится к нахождению условий финитности (инфинитности) одномерного движения частицы в радиальном направлении в поле, описываемом эффективной потенциальной функцией 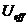
12.3. О траектории движения частицы.
Представим компоненты импульса, записанного в полярных координатах, следующим образом:
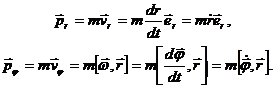
Далее, т.к. угол между вектором угловой скорости 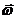
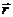
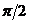
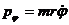
Тогда из (12.10а, 12.12 и 12.14) для энергии и момента импульса частицы, движущейся в центральном поле, получаем
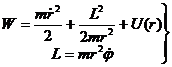
Из второго уравнения (12.15) получаем
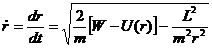
Разделяя переменные, находим в неявном виде зависимость 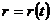
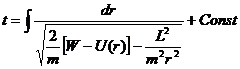
Из первого уравнения (12.15) имеем
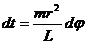
Исключив из уравнений (12.15) время 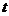
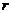
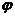
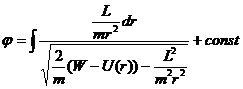
Значения 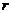
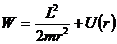
определяют границы области движения по расстоянию от центра поля. При выполнении равенства (12.18) радиальная скорость 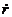
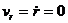
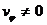
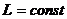
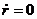
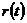
Если область допустимого изменения 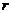
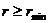
Если область изменения 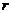
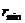
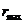
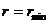
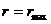
За время прохождения одной петли (от 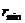
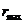
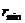
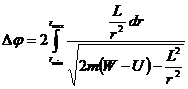
Условие замкнутости траектории: траектория будет замкнутой, если 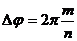
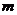
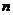
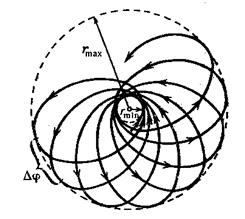
на угол, равный рациональной части от 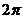
Тогда через 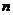
вектор точки, сделав 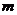
первоначальным значением, т.е. траектория замкнется.
Однако такой исход является скорее исключением,
нежели правилом. Существуют лишь два типа центральных
полей, в которых все траектории финитных движений
замкнуты. Это поля, где зависимость потенциальной энергии
от расстояния от центра поля имеет вид:
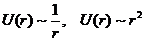
Задача Кеплера (Кеплерова задача) — задача о движении частицы в поле центральных сил, убывающих обратно пропорционально квадрату расстояния от центра поля. Этому закону подчиняются силы гравитационного притяжения между точечными массами (или телами, обладающими сферической симметрией), а также кулоновские силы, действующие между точечными электрическими зарядами. Поэтому такие поля являются важнейшим случаем центральных полей.
В таком поле потенциальная энергия частицы определяется выражением
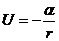
где 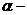
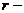
Рассмотрим случай, когда 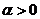

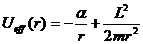
от расстояния от центра поля показана на рисунке.
При 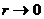
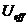
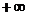
она стремится к нулю со стороны отрицательных
значений; при 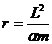
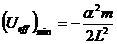
Из рисунка видно, что движение частицы будет инфинитным при 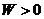
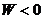
Форму траектории получаем интегрированием формулы (12.15) после подстановки 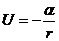
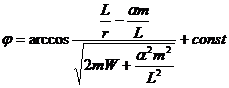
Выбирая начало отсчета угла 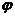
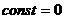
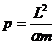
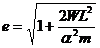
получим уравнение траектории в виде:
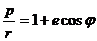
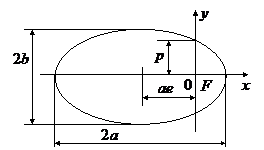
Приложение. Выражение (13.6) – уравнение конического сечения с фокусом в начале координат в полярных координатах; 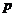
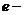
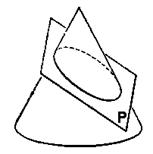
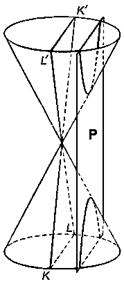
Коническими сечениями называют эллипс, параболу и гиперболу, т.к. их можно получить на поверхности
круглого конуса в пересечении с плоскостью 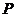
вершину конуса. При этом поверхность конуса предполагается
неограниченно продолженной в обе стороны от вершины.
Если плоскость 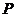
коническое сечение есть эллипс. Эллипсом называется геометрическое
место точек, сумма расстояний от которых до двух данных точек,
называемых его фокусами, есть величина постоянная. Отношение
фокусного расстояния эллипса к длине его большой оси называется
эксцентриситетом эллипса 
Если плоскость 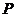
называют геометрическое место точек, равноотстоящих
от данной точки, называемой фокусом, и данной прямой
называемой директрисой. Исходя из её определения,
эксцентриситет параболы принимают равным единице
( 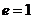
Если плоскость 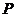
( 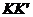
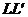
Гиперболой называется геометрическое место точек, разность
расстояний от которых до двух данных точек, называемых
фокусами, есть величина постоянная. Величина, определяемая
как отношение фокусного расстояния к длине действительной
оси (длина отрезка, соединяющего вершины гиперболы), называется
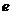
Из аналитической геометрии известно, что все эллипсы (кроме
окружности), параболы и гиперболы обладают следующим свойством: для
каждой из этих линий остается неизменным отношение
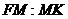
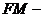
произвольной её точки 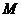
данной точки 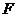
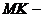
до данной прямой
Обобщая сказанное, можно дать
общее определение конического
сечения (эллипса, гиперболы и
параболы): коническое сечение есть
геометрическое место точек, отношение
расстояний которых до данной точки
(фокуса) и до данной прямой (директрисы) есть величина постоянная 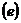
для эллипса 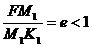
для параболы 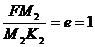
для гиперболы 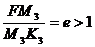
Из (13.5) следует, что при 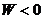
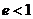
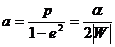
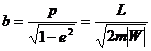
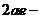
Из уравнения (13.6) следует, что точка с 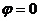
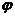
Наименьшее и наибольшее расстояния частицы от центра поля (фокуса эллипса) составляют (из 13.6)
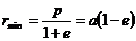
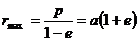
и зависят только от энергии частицы, поскольку из (13.7),
следует, что большая полуось эллипса 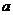
энергии, но не от момента импульса частицы).
Примечание. Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце –
первый закон Кеплера.
Время обращения по эллиптической орбите (период 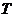
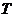
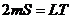
где 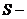
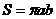
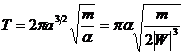
Тот факт, что квадрат периода обращения должен быть пропорционален кубу линейных размеров орбиты, составляет содержание третьего закона Кеплера.
Отметим, что период обращения, как следует из (13.11) зависит только от энергии частицы.
При 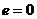
В случае если энергия частицы 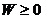
Если энергия частицы положительна 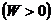
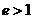
поля определяется выражением
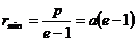
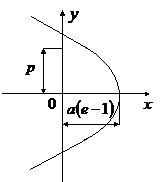
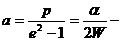
В случае, когда полная энергия частицы
эксцентриситет кривой 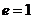
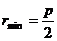
Этот случай реализуется, если частица начинает свое движение
из состояния покоя на бесконечности.
Используя выражение (13.9, 13.12 и 13.14) и соответствующие значения эксцентриситета, можно найти скорость частицы в перигелии при движении по всем рассмотренным траекториям. В точке поворота (перигелии) 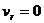
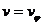
По окружности ( 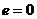
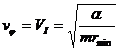
движению по параболе ( 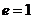
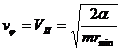
Если скорость частицы лежит в интервале
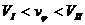
то её траекторией является эллипс ( 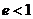
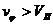
то траектория частицы имеет форму гиперболы ( 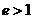
В небесной механике 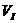
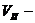
Обратимся теперь к движению в поле отталкивания, в котором потенциальная энергия частицы определяется выражением
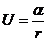
где 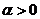
В этом случае эффективная потенциальная энергия частицы
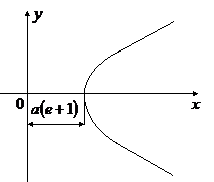
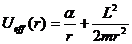
монотонно убывает от бесконечности до нуля
при изменении расстояния от центра поля от нуля до
бесконечности 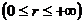
энергия частицы 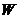
и её движение инфинитно. Все вычисления в этом случае
полностью аналогичны приведенным выше.
Траектория частицы является гиперболой
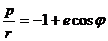
где характеристики кривой по-прежнему определяются
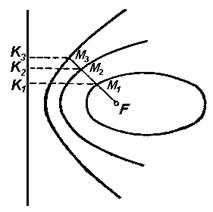
Двигаясь по такой траектории, частица проходит мимо центра поля, как показано на рисунке. Расстояние
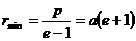
В заключение рассмотрения задачи Кеплера укажем, что при движении в поле центральных сил, котором потенциальная энергия частицы определяется выражением 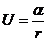
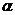
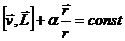
что легко проверить непосредственным вычислением, взяв от него производную по времени.
Сохраняющийся вектор (13.19) направлен вдоль большой оси от фокуса к перигелию и равен по величине 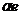
Интеграл движения, наряду с такими сохраняющимися величинами, полная энергия 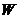
Видео:Степаньянц К. В. - Теоретическая механика I - Движение в центральном полеСкачать

Энергия
1.77. Найти приращение энергии ΔE, если: а) Е1=2 Дж, E2=5 Дж, б) E1=10 Дж, E2=8 Дж.
1.78. Для указанных в задаче 1.77 начальной Е1 и конечной Е2 энергий найти убыль энергии -ΔE.
1.79. Первоначально покоившаяся частица, находясь под действием силы F=1ex+2ey+3ez (Н), переместилась из точки (2, 4, 6) (м) в точку (3, 6, 9) (м). Найти кинетическую энергию T частицы в конечной точке.
1.80. Находясь под действием постоянной силы с компонентами (3, 10, 8) (Н), частица переместилась из точки 1 с координатами (1, 2, 3) (м) в точку 2 с координатами (3, 2, 1) (м). Определить: а) Какая при этом совершается работа А? б) Как изменилась кинетическая энергия частицы?
1.81. Доказать соотношение: Tл = Tц + mVC 2 /2, где Tл — кинетическая энергия системы материальных точек, определяемая в лабораторной системе отсчета (л-системе), Tц — кинетическая энергия, определяемая в системе центра масс (ц-системе), m — суммарная масса системы, VC — скорость центра масс в л-системе.
1.82. Потенциальная энергия частицы в некотором силовом поле определяется выражением U=1,00x+2,00y 2 +3,00z 3 (U в Дж, координаты в м). Найти работу А, совершаемую над частицей силами поля при переходе из точки с координатами (1,00; 1,00; 1,00) в точку с координатами (2,00; 2,00; 2,00).
1.83. Потенциальная энергия частицы определяется выражением U=a(x 2 +y 2 +z 2 ), где a — положительная константа. Частица начинает двигаться из точки с координатами (3,00; 3,00; 3,00) (м). Найти ее кинетическую энергию T в момент, когда частица находится в точке с координатами (1,00; 1,00; 1,00) (м).
1.84. Два тела соскальзывают без трения и без начальной скорости с наклонных плоскостей 1 и 2 (рис. 1.12). а) Сравнить скорости тел v1 и v2 в конце соскальзывания. б) Одинаковы ли времена соскальзывания t1 и t2?
1.85. Имеются две наклонные плоскости, совпадающие с хордами одной и той же окружности радиуса R (рис. 1.13). С каждой из них соскальзывает без трения и без начальной скорости небольшое тело. Для какой из плоскостей время соскальзывания больше?
1.86. Небольшое тело массы m устанавливают в верхней точке наклонной плоскости высоты h и сообщают ему начальную скорость v0, в результате чего оно начинает сползать по плоскости вниз (рис. 1.14). Поверхность плоскости неоднородна, поэтому скорость сползания изменяется некоторым произвольным образом. Однако в нижней точке плоскости скорость имеет первоначальное значение v0. Какую работу А совершают силы трения на всем пути движения тела?
1.87. Небольшое тело начинает скользить без трения с вершины сферы радиуса R вниз (рис. 1.15). На какой высоте h над центром сферы тело отделится от поверхности сферы и полетит свободно?
1.88. По желобу, имеющему форму, показанную на рис. 1.16 (горизонтальный участок желоба сдвинут относительно наклонного в направлении, перпендикулярном к рисунку), с высоты h начинает скользить без трения небольшое тело (материальная точка). а) При каком минимальном значении высоты h тело опишет полную петлю, не отделяясь от желоба? б) Чему равна при таком значении h сила F давления тела на желоб в точке A?
1.89. Градиент скалярной функции φ в некоторой точке P представляет собой вектор, направление которого совпадает с направлением l, вдоль которого функция φ, возрастая по величине, изменяется в точке P с наибольшей скоростью. Модуль этого вектора равен значению dφ/dl в точке P. Аналитически это можно записать следующим образом: ∇φ = (dφ/dl)el. 1. Исходя из этого определения, найти выражения для: а) ∇r, б) ∇(1/r), в) ∇f(r), где r — модуль радиус-вектора точки P. 2. Убедиться в том, что такие же выражения получаются с помощью формулы: ∇φ = (∂φ/∂x)ex + (∂φ/∂y)ey + (∂φ/∂z)ez.
1.90. Потенциальная энергия частицы имеет вид: a) U=α/r, б) U=kr 2 /2, где r — модуль радиус-вектора r частицы; α и k — константы (k>0). Найти силу F, действующую на частицу, и работу А, совершаемую над частицей при переходе ее из точки (1, 2, 3) в точку (2, 3, 4).
1.91. Потенциальная энергия частицы имеет вид U = a (x/y — y/z), где a — константа. Найти: а) силу F, действующую на частицу, б) работу А, совершаемую над частицей силами поля при переходе частицы из точки (1, 1, 1) в точку (2, 2, 3)
1.92. Потенциальная энергия частицы, находящейся в центрально-симметричном силовом поле, имеет вид U = a/r 3 — b/r 2 , где a и b — положительные константы. а) Имеется ли у этой частицы положение устойчивого равновесия по отношению к смещениям в радиальном направлении? б) Нарисовать примерную кривую зависимости U от r.
1.93. Частица движется по окружности в поле центральной силы, обратно пропорциональной квадрату расстояния от силового центра. В каком соотношении находятся в этом случае кинетическая T, потенциальная U и полная Е энергии частицы?
1.94. Частица массы m находится в силовом поле вида F=-(α/r 2 )er (α — положительная константа, r — модуль, а er — орт радиус-вектора частицы). Частицу поместили в точку с радиус-вектором r0 и сообщили ей начальную скорость v0, перпендикулярную к r0. По какой траектории будет двигаться частица?
1.95. При каком условии траекторией частицы из предыдущей задачи будет окружность?
1.96. Невесомая нерастяжимая нить может скользить без трения по изогнутому желобу (рис. 1.17). К концам нити прикреплены грузы массами m1=3,00 кг и m2=1,00 кг. Груз массы m1 поднимают настолько, чтобы груз массы m2 коснулся пола, и отпускают. Высота h1=1,00 м. На какую высоту h2 над полом поднимется груз массы m2 после того, как груз массы m1 ударится о пол?
1.97. Автомобиль массы m=1,00 т ехал некоторое время по горизонтальному участку дороги с постоянной скоростью v=80 км/ч. При въезде на подъем, образующий с горизонтом угол α=10,0°, для того чтобы сохранить прежнюю скорость, пришлось, «прибавив газ», увеличить вращающий момент, приложенный к ведущим колесам, в η=6,20 раза. Считая силу F сопротивления воздуха движению автомобиля пропорциональной квадрату скорости, определить коэффициент k в формуле F=kv 2 . Трением в шинах пренебречь.
1.98. По резиновому шнуру, подвешенному одним концом к кронштейну (рис. 1.18), может скользить с независящим от скорости трением муфта массы m = 0,300 кг. Трение характеризуется силой F = 0,294 Н. Длина недеформированного шнура l0=1,00 м, коэффициент пропорциональности между упругой силой и удлинением шнура k = 560 Н/м. На нижнем конце шнура имеется упор. Муфту поднимают в крайнее верхнее положение и отпускают. Пренебрегая внутренним трением в шнуре, размерами муфты, а также массами шнура и упора, определить: а) удлинение шнура Δl в момент достижения муфтой упора, б) скорость муфты v в этот момент, в) максимальное удлинение шнура Δlmax.
Ошибка в тексте? Выдели её мышкой и нажми
Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!
Видео:Движение заряженной частицы в магнитном поле | Физика ЕГЭ с Никитой АрхиповымСкачать

Частица массы m движется по окружности радиусом R. Нормальное ускорение частицы подчиняется уравнению: a= at^2, где α − размерная
Видео:Физика - движение по окружностиСкачать

Ваш ответ
Видео:55. Движение частиц в электромагнитных поляхСкачать

решение вопроса
Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,022
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
🌟 Видео
Урок 276. Сила Лоренца. Движение заряженных частиц в магнитном полеСкачать

Теоретическая механика. Лекция №5. Движение в центральном полеСкачать

Халилов В. Р. - Теоретическая механика - Движение в центрально-симметричном полеСкачать

Элементарные частицы, масса и гравитация | Физик Алексей СемихатовСкачать

Физика | Равномерное движение по окружностиСкачать

Движение материальной точки по окружности | Физика ЕГЭ, ЦТСкачать

Теормех. 2021-ноя-17. Движение в центральном полеСкачать

Центробежная силаСкачать

Физика - импульс и закон сохранения импульсаСкачать

Механика - Движение в поле центральных сил. Момент импульсаСкачать

Форш П. А. - Теоретическая механика - Интегрирование уравнений движения. Движение в центральном полеСкачать

Теория движения заряженных частиц в электрическом поле .Часть 1Скачать

🔴 ЕГЭ-2024 по физике. Разбор варианта №19 (Демидова М.Ю., 30 вариантов, ФИПИ, 2024)Скачать

Теоретическая механика 6 Движение в центрально симметричном полеСкачать

Аналитическая механика 5. Движение точки в центральном поле.Скачать