В чем сходства и различия окружности и круга (4 видео)

Чем отличается окружность от круга

В обычной жизни нам приходится замечать множество предметов, которые по своей форме напоминают окружности и круги, но редко кто задумывается о том, чем окружность отличается от круга и что у них общего.

Окружность – это замкнутая плоская кривая, все точки которой равноудалены от заданной точки (центра окружности). Окружностью называют линию, которая ограничивает круг. Правильную окружность можно изобразить с помощью циркуля. Ножку с иголкой нужно установить в задуманную точку, и тогда ножка с карандашиком начертит замкнутую линию. Эта линия разделяет плоскость на две части: внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, т. к. плоскость в общем понимании не имеет границ. Для отличия, можно заштриховать внутреннюю область. Часть, которая осталась внутри, называется кругом.

Окружность имеет центр — это начальная точка нарисования циркулем. Если задуманная точка лежит на окружности, это означает, что она ей принадлежит. Можно обозначить дуги окружности, ими будут любые 2 точки, ограничивающие окружность, т. е. любые две точки A и B окружности разбивают ее на две части; каждая из этих частей и называется дугой. Если провести линию через эти точки, то получим хорду. А хорда, проходящая через центр окружности, имеет название диаметра. Если же от центра провести линии к точке на окружности, то получится радиус окружности.

Круг – является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Пространство, закрепленное границей, включая центр круга принадлежит кругу. Если провести линию от одной точки на границе круга до другой через центр, то такое расстояние будет называться диаметром круга. Если от центра круга провести прямую линию до любой отметки на его границе, то это расстояние называется радиус. Два радиуса, равноудалённые от центра круга, будут соответствовать его диаметру. Следовательно, диаметр в два раза больше радиуса. Если от одной точки круга провести хорду, то хорда и соответствующая ей дуга будет образовывать сегмент круга. Окружность и круг имеют общий радиус и диаметр.

Отличие окружности и круга

Окружность, как любая линия имеет длину, а круг, как любая геометрическая фигура имеет площадь. Круг имеет площадь, но её нет у окружности. Круг содержит центр окружности, а окружность, содержит сам круг. Без окружности не было бы круга, но она существует самостоятельно. Окружность проводит границу круга снаружи, а круг – внутренняя часть окружности. И круг, и окружность имеют одинаковый центр.

Выводы:

Окружность представляет собой замкнутую линию.
Круг, это пространство, ограниченное окружностью.
Радиус окружности, равен радиусу круга.
Диаметр делит окружность и круг на два равных полукруга.
Окружность является границей круга.
Если начертить заштрихованную окружность, то её можно считать кругом и наоборот.
Круг и окружность имеют единый центр.
У окружности есть длина, а у круга её нет.

Содержание

Ресурсы:
Сходства и различия круга и окружности
Окружность и круг
Определения
Различия
Сходства
Формулы
Окружность и прямая
Окружность и угол
Что мы узнали?
Разница между окружностью и кругом
Чем отличается окружность от круга
Ресурсы:
Отличие окружности и круга
💥 Видео

Ресурсы:

Большой энциклопедический словарь (БЭС)

Окружность – это замкнутая плоская кривая, все точки которой равноудалены от заданной точки (центра окружности)

Видео:Окружность и круг, 6 классСкачать

Сходства и различия круга и окружности

Видео:Окружность. Круг. 5 класс.Скачать

Окружность и круг

Средняя оценка: 4.7

Всего получено оценок: 418.

Средняя оценка: 4.7

Всего получено оценок: 418.

Окружность и круг – это две разные фигуры, которые частенько путают в математике 6 класса. Поэтому имеет смысл обсудить эту тему более подробно.

Видео:5 класс, 22 урок, Окружность и кругСкачать

Определения

Круг – это часть пространства, ограниченная окружностью. Окружность – это множество точек, равноудаленных от одной точке, называемой центром окружности.

Видео:Чем отличается круг от окружностиСкачать

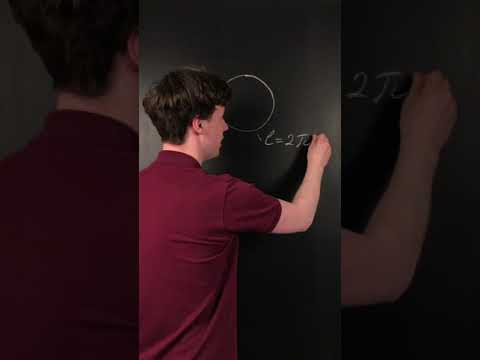
Различия

Окружность – это линия. Круг – это плоская фигура. Окружность не может иметь площади, тогда как круг ее имеет.

Рис. 1. Круг и окружность.

На этом, пожалуй, различия круга и окружности заканчиваются. Но стоит сказать еще и о том, что в геометрии чаще звучит название окружности.

Круг имеет площадь, но в задачах мы чаще ищем длину окружности. На длину окружности завязаны некоторые свойства вписанной и описанной окружности треугольника, поэтому сложилась некая традиция использования окружности вместо круга. Но путать эти фигуры ни в коем случае нельзя.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Сходства

Сходства заключаются в характеризующих отрезках. Их несколько для окружности и круга: хорда, радиус и диаметр.

Хорда это отрезок, соединяющий две точки окружности. Хорда может не проходить через центр окружности, а может и проходить.

Если хорда проходит через центр окружности, то она зовется диаметром. Диаметр это отрезок, соединяющий две точки окружности и проходящий через ее центр. Диаметр используется при нахождении площади и длины окружности.

Радиус это любой отрезок, соединяющий центр окружности и точку на окружности. Радиус может использоваться вместо диаметра, так как равен его половине.

Видео:Математика 5 класс (Урок№26 - Окружность и круг. Сфера и шар.)Скачать

Формулы

Формула площади актуальна только для круга. Окружность не может иметь площади.

$R= >$-то есть радиус равен половине диаметра. Соответственно это равенство можно подставить в формулу площади и получить еще одну формулу. Или просто найти диаметр или радиус через эту формулу и подставить в уже приведенную формулу.

Существует формула, которая позволяет найти длину окружности. Что такое длина окружности? Если условно распрямить линию окружности, то получится прямая, длину которой можно найти по формуле:

$L=pi*d$ – диаметр, так же, как и в площади можно заменить диаметром.

Рис. 2. Длина окружности.

Видео:Радиус и диаметрСкачать

Окружность и прямая

Положение окружности и прямой на плоскости это отдельная тема для разговора. Прямая на плоскости может:

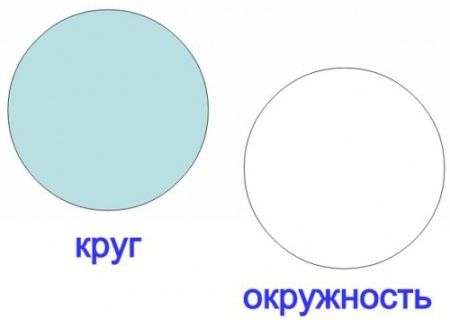
Пересекать окружность
Не пересекать окружность
Касаться окружности

Прямая, пересекающая окружность зовется секущей и имеет две общие точки с окружностью.

Отдельный интерес имеет касательная прямая, то есть прямая, которая имеет одну общую точку с окружностью. Дело в том, что эта прямая имеет свойство, которое часто помогает в решении задач.

Запомните, радиус, проведенный в точку касания перпендикулярен касательной.

Рис. 3. Окружность и прямая.

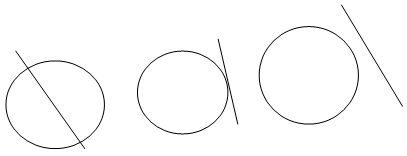
Видео:Круг. Окружность (центр, радиус, диаметр)Скачать

Окружность и угол

Окружность и угол связаны, потому как окружность это наиболее яркий пример полного угла. То есть, если провести какой либо отрезок и повернуть его вокруг своего начала на 360 градусов, то получится окружность.

Углом в окружности измеряется дуга. Дуга это часть окружности, ограниченная двумя радиусами. Два радиуса и дуга представляют собой сектор.

Видео:МАТЕМАТИКА 5 класс: Окружность и кругСкачать

Что мы узнали?

Из статьи мы узнали о том, что круг – это плоская фигура, а окружность – это линия. Мы познакомились с характеристиками этих понятий и узнали свойства круга и окружности.

Видео:КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 классСкачать

Разница между окружностью и кругом

На уроках геометрии в школе все мы изучали свойства различных фигур и линий. Каждая из них имеет свои особенности, а порой некоторые из них взаимосвязаны друг с другом. Взять для примера хотя бы круг и окружность – между ними есть определенная связующая линия. Только вот какая? Давайте вместе разберемся в этом вопросе.

Окружность представляет собой бесчисленное множество точек, которые находятся на одинаковом расстоянии от одной единственной, называемой центром окружности. Соединенные между собой точки формируют кривую линию, которая и будет окружностью. Все точки, которые находятся на другом расстоянии от центра окружности, не будут находиться на этой линии, поэтому не будут входить в окружность. Соответственно, окружность – это геометрическая фигура, которая представляет собой определенную линию, а все, что находится внутри нее либо снаружи, к окружности не относится. По этой причине имеется четкое понятие, что окружность делит всю плоскость на две части – внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, поскольку плоскость в общем понимании не имеет границ.

Круг является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Все внутреннее пространство, а также центр круга принадлежат ему, таким образом, можно говорить о том, что круг представляет собой некую площадь пространства, ограниченную множеством точек. А поскольку эти точки равноудалены от центра, то границей круга будет окружность. Все внешнее пространство кругу не принадлежит, зато он охватывает всю ту часть плоскости, которая очерчена при помощи окружности.

Различия между кругом и окружностью не столь велики, поскольку эти фигуры представляют собой неисчисляемое количество точек плоскости, находящихся от одной центральной точки на одинаковом расстоянии. Но важным отличительным признаком является тот факт, что внутреннее пространство не принадлежит окружности, но обязательно является составной частью круга. Иными словами, круг представляет собой не только окружность, которая является его границей, но также и то бесконечное число точек, находящихся внутри этой окружности.

Видео:МЕРЗЛЯК-6. КРУГ И ОКРУЖНОСТЬ. ПАРАГРАФ-24Скачать

Чем отличается окружность от круга

Отличие окружности и круга

Выводы:

Окружность представляет собой замкнутую линию.
Круг, это пространство, ограниченное окружностью.
Радиус окружности, равен радиусу круга.
Диаметр делит окружность и круг на два равных полукруга.
Окружность является границей круга.
Если начертить заштрихованную окружность, то её можно считать кругом и наоборот.
Круг и окружность имеют единый центр.
У окружности есть длина, а у круга её нет.

Ресурсы:

Большой энциклопедический словарь (БЭС)

Видео:Видеоурок 14. Круг и окружность. Математика 3 классСкачать

Отличие окружности и круга

Частное учреждение профессионального образования

«Юридический полицейский колледж»

Реферат

на тему: «Круг, окружность, шар, сфера их отличия»

Студентка группа 18ПД

Проверил: Щербаков К.В.

Окружность– это замкнутая плоская кривая, все точки которой равноудалены от заданной точки (центра окружности). Окружностью называют линию, которая ограничивает круг. Правильную окружность можно изобразить с помощью циркуля. Ножку с иголкой нужно установить в задуманную точку, и тогда ножка с карандашиком начертит замкнутую линию. Эта линия разделяет плоскость на две части: внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, т. к. плоскость в общем понимании не имеет границ. Для отличия, можно заштриховать внутреннюю область. Часть, которая осталась внутри, называется кругом.

Окружность имеет центр — это начальная точка нарисованная циркулем. Если задуманная точка лежит на окружности, это означает, что она ей принадлежит. Можно обозначить дуги окружности, ими будут любые 2 точки, ограничивающие окружность, т. е. любые две точки A и B окружности разбивают ее на две части; каждая из этих частей и называется дугой. Если провести линию через эти точки, то получим хорду. А хорда, проходящая через центр окружности, имеет название диаметра. Если же от центра провести линии к точке на окружности, то получится радиус окружности.

Круг– является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Пространство, закрепленное границей, включая центр круга принадлежит кругу. Если провести линию от одной точки на границе круга до другой через центр, то такое расстояние будет называться диаметром круга. Если от центра круга провести прямую линию до любой отметки на его границе, то это расстояние называется радиус. Два радиуса, равноудалённые от центра круга, будут соответствовать его диаметру. Следовательно, диаметр в два раза больше радиуса. Если от одной точки круга провести хорду, то хорда и соответствующая ей дуга будет образовывать сегмент круга. Окружность и круг имеют общий радиус и диаметр.

Отличие окружности и круга

Пример: Таким образом, круг является некоторым участком плоскости, а окружность — всего лишь граница этого участка. Чтобы лучше понять это, представьте себе кольцо (я возьму что-нибудь круглое и съедобное, например, бублик). Это и будет нашей окружностью. Бублик имеет дырочку. Дырочка к бублику не относится, дырочку от бублика съесть нельзя, а вот сам бублик можно кушать. Понимаете? Всё, что лежит внутри окружности, к самой окружности не относится (за исключением окружности с нулевым радиусом). Теперь мысленно вставим в бублик круглую булочку, так, чтобы булочка идеально вписалась в бублик (чтобы не было зазоров и проч.). Булочка и бублик образуют круг. Бублик будет границей этого круга, частью круга (бублик принадлежит кругу, а так как за бублик мы взяли окружность, то окружность принадлежит кругу). И булочку, и бублик можно съесть. Пример с бубликом и булочкой является самым наглядным примером, который при желании можно повторить дома, хотя здесь достаточно всё представить мысленно.

Когда людям задают вопрос, чем отличается сфер от шара, многие попросту пожимают плечами, думая, что фактически это одно и то же (аналогия с кругом и окружностью).

В повседневной жизни мы редко говорим сфера, чаще шар или шарик. И не все понимают какая разница между этими двумя геометрическими понятиями. Наверное можно сказать, что сфера это внешняя оболочка шара. Воздушный шарик, например, на самом деле не шар, а сфера. При условии, конечно, его абсолютной «круглости». Как я понимаю, то у шара абсолютно все точки поверхности равноудалены от его центра, а у сфер это условие не является обязательным.

Пример: Апельсин, футбольный мяч, арбуз, похожи на шар. Из всех тел заданного объёма шар имеет наименьшую поверхность. Поверхность шара называют сферой. Расстояние от точек сферы до её центра называется радиусом сферы и обычно обозначается R. Радиусом также называется любой отрезок, соединяющий точку сферы с её центром.