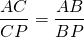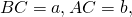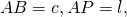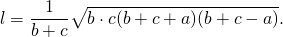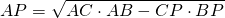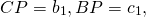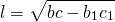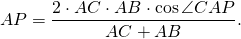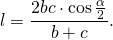Биссектриса треугольника и угла разница

Треугольник в геометрии основная фигура, которую нельзя разделить на составляющие. Отрезок прямой линии, соединяющий вершину с противоположной стороной, при условии разделения угла пополам, это биссектриса треугольника. Так как данная фигура содержит 3 угла, соответственно, из каждого можно провести линию, делящую его на равные компоненты.

Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Свойства биссектрисы

Равносторонняя треугольная фигура характеризуется не только равенством сторон, но внутренние углы также одинаковы, при этом они составляют 60° каждый.

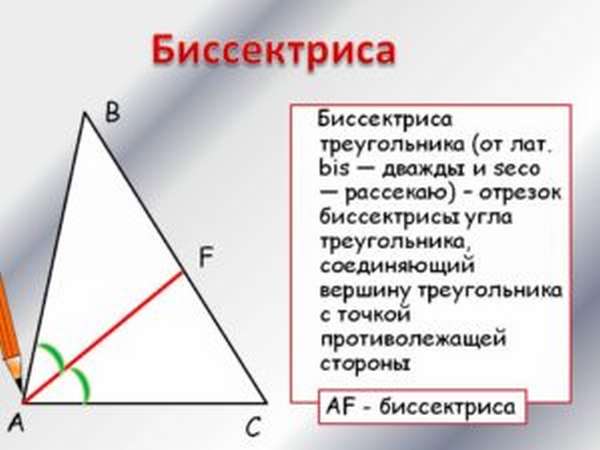
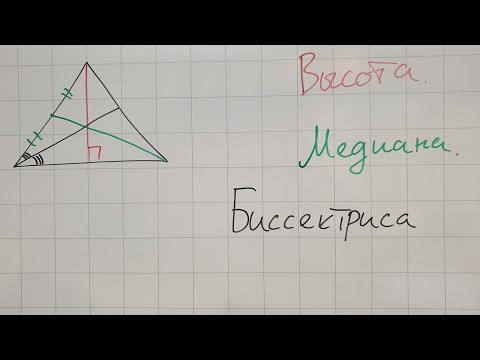
Поэтому проведенная биссектриса одновременно является высотой, медианой. Она обладает не только своими качествами, но и характеристиками высоты, медианы треугольника:

• делит противоположные стороны на равные части,
• перпендикулярна к противолежащей стороне,
• в точке пересечения 3 линий каждый отрезок делится в соотношении 2:1, считая от вершины (свойство медианы),
• из центра пересечения можно одновременно провести окружность внутри и вокруг фигуры,
• линии, делящие на равные части внешние углы правильного треугольника, параллельны противоположно расположенным сторонам фигуры,
• все 3 отрезка, проведенные из вершин, равны по длине.

Это интересно! Урок геометрии: как найти по формуле периметр треугольника

Наиболее простая формула, определяющая, как найти биссектрису треугольника, выражается через радиус вписанной (r) или описанной (R) окружности:

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Характеристика внутренних линий

Основное свойство биссектрисы треугольника с равными боковинами: отрезок, опущенный из вершины, одновременно является медианой, высотой.

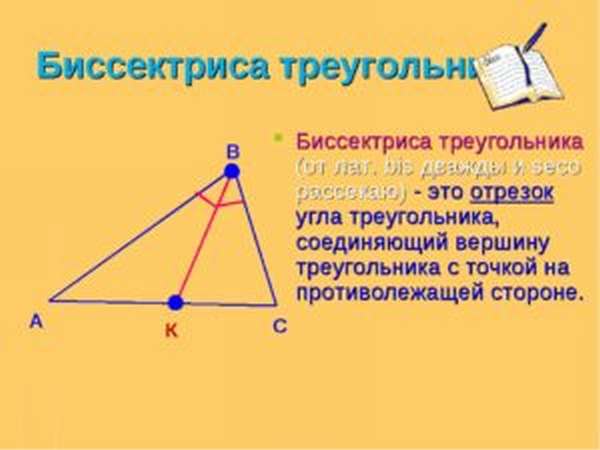
При этом, кроме разделения угла на 2 равные части, линия характеризуется следующими качествами:

• делит нижнее основание пополам,
• служит перпендикуляром к противолежащей стороне,
• отрезок луча, разделяющий внешний угол вершины с равными боковинами, параллелен основанию.

Важно! Биссектрисы равных углов у основания также равны между собой по длине.

При этом верно обратное утверждение: когда 2 биссектрисы равны между собой, то треугольник считается равнобедренным.

Если вершина содержит 90° (прямой угол), то отрезки, опущенные на катеты, пересекаются под 45°. В этом случае определить размер искомого отрезка помогает теорема Пифагора.

Это интересно! Что значит вертикально и как выглядит вертикальная линия

Пример

В треугольнике АВС вершина А содержит 90°. Отрезок АД служит высотой, биссектрисой и медианой одновременно. Образованы 2 прямоугольные трехсторонние фигуры: АВД и АСД, у которых равны основания (ВД=СД). Требуется найти длину отрезка АД.

По теореме Пифагора АД2 = АВ2-ВД2. Отсюда АД = √АВ2-ВД2.

Это интересно! Изучаем символы: как обозначается в математике площадь

Видео:3 свойства биссектрисы #shortsСкачать

Соотношение со сторонами треугольника

Слово, в переводе с латинского языка, обозначает «сечение поперек». Чем отличается биссектриса от других главных и второстепенных отрезков треугольной фигуры, было известно еще Архимеду, который в своих трудах активно использовал ее свойства для определения сторон многоугольников. При этом количество сторон должно быть кратным трем. Классическая теорема о биссектрисе гласит, что линия разделяет противоположную сторону на 2 отрезка, отношение которых друг к другу такое же, как соотношение двух соприкасающихся к основанию сторон.

Пример

Дан треугольник АВС. Из вершины А проведена биссектриса АД, разделяющая сторону ВС на 2 отрезка (ДВ и ДС). Смысл теоремы сводится к равенству нескольких величин: ВД/АВ=СД/АС и ВД/ДС=АВ/АС. Лучше понять формулу помогает фото треугольника с проведенной линией.

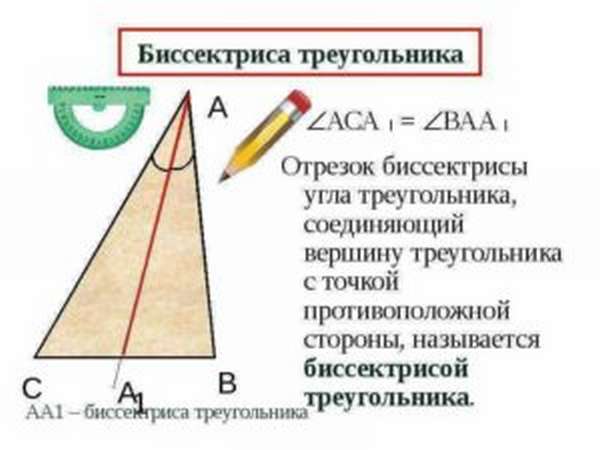
• любая биссектриса, выпущенная из вершины неправильного треугольника, расположена между медианой и высотой, выходящей из этого же места,
• все точки, расположенные на отрезке, удалены от сторон по бокам вершины на одинаковое расстояние,
• лучи, разделяющие пополам внешний и внутренний угол треугольной фигуры, перпендикулярны между собой,
• все отрезки, делящие на равные части внутренние углы, пересекаются в строго определенной точке, которая служит центром вписанной в эту фигуру окружности,
• если две биссектрисы равны по длине, то фигура – равнобедренная, если все одинакового размера, треугольник – правильный.

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Способы построения

Зная, что такое биссектриса, легко определить расположение отрезка в треугольной фигуре. Для построения применяется несколько способов:

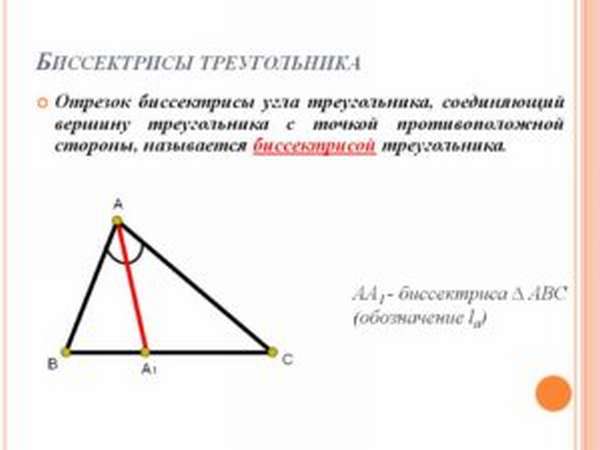
1. Известен угол, из которого исходит прямая, делящая его на равные сегменты. Значение делится пополам. На рисунке с помощью транспортира строится нужный отрезок.
2. Если параметры угла неизвестны, его измеряют транспортиром, делят пополам, затем проводят искомую линию.
3. Оригинальный способ построить нужный отрезок с помощью карандаша, линейки и циркуля. Из любой вершины проводится окружность произвольного радиуса. Главное, что величина должна быть меньше, чем прилегающая сторона. Место пересечения с каждой стороной считается центром для еще двух окружностей с таким же шагом циркуля. Нарисовать еще два круга, которые пересекаются между собой два раза. Через полученные точки и вершину под линейку проводится прямая, которая и есть настоящая биссектриса внутреннего угла.
4. Построить треугольник по известной длине трех отрезков (АВ, ВС, АС) можно с помощью линейки и циркуля. На произвольной прямой линии обозначить сегмент, равный АВ. Из точки А провести окружность с шагом циркуля равным АС, а затем аналогично из точки В провести окружность с шагом ВС. Точка пересечения – вершина искомой треугольной фигуры (С), в которой легко определяются биссектрисы, учитывая их характеристики.

Важно! Если известны только размеры биссектрис, то построить по данным параметрам возможно бесконечное количество подобных фигур.

Видео:Свойство биссектрисы треугольника с доказательствомСкачать

Полезное видео

Видео:Биссектриса угла. Геометрия 7 класс.Скачать

Подведем итоги

Зная значение и характеристики главных линий в треугольной фигуре, можно решать много задач, определять величину углов, длину, изучать соотношение сторон.

Видео:ПОСТРОЕНИЕ БИССЕКТРИСЫ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Биссектриса — это луч разрезающий угол пополам, а также отрезок в треугольнике обладающий рядом свойств

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о таком термине, как БИССЕКТРИСА.

Это понятие широко применяется в геометрии. И каждый школьник в России знакомится с ним уже в 5 классе. А после эта величина часто используется для решения различных задач.

Видео:Построение биссектрисы угла. 7 класс.Скачать

Биссектриса — это.

Биссектриса – это луч, который выходит из вершины треугольника и делит ее ровно на две части.

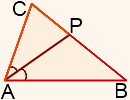
Также под биссектрисой принято понимать и длину отрезка (что это?), который начинается в вершине треугольника, а заканчивается на противоположной от этой вершины стороне.

Есть еще понятие «биссектриса угла», которая является лучом и точно так же делит угол (любой, не обязательно треугольника) пополам:

Само понятие БИССЕКТРИСА пришло к нам из латинского языка. И название это весьма говорящее. Оно состоит из двух слов – «bi» означает «двойное, пара», а «sectio» можно дословно перевести, как «разрезать, поделить».

Вот и получается, что само слово БИССЕКТРИСА – это «разрезание пополам», что собственно и отражается в определении термина, который мы только что привели.

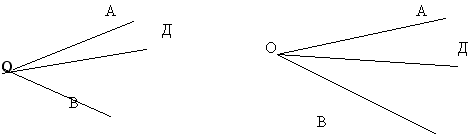
А сейчас задачка на закрепление материала. Посмотрите на эти рисунки и скажите, на каком изображена биссектриса. Подумали? Правильно, на втором.

На первом луч, выходящий из угла АОВ, явно не делит его пополам. На втором это соотношение углов более очевидно, а потому можно предположить, что луч ОД является БИССЕКТРИСОЙ. Хотя, конечно, на сто процентов это утверждать сложно.

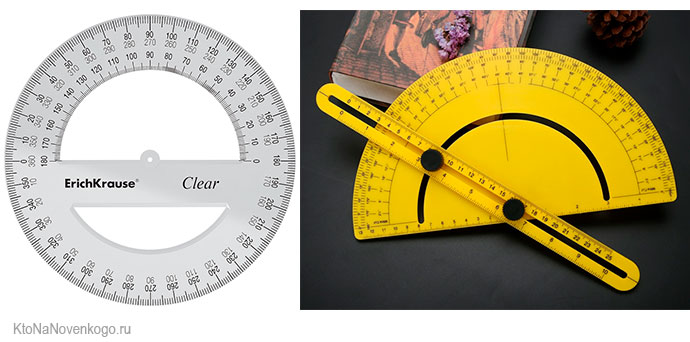
Для более точного определения используют специальные инструменты. Например, транспортир. Это такой инструмент в виде полусферы из металла или пластмассы. Вот как он выглядит:

Хотя есть еще вот такие варианты:

Наверняка у каждого такие были в школе. И пользоваться ими весьма просто. Надо только ровненько совместить основание транспортира (прямоугольная линейка) с основанием треугольника, а после на полусфере отметить значение, которое соответствует размеру угла.

И точно по такой же схеме можно поступить наоборот – имея транспортир, начертить угол необходимого размера. Чаще всего – от 0 до 180 градусов. Но на втором рисунке у нас транспортир, который помогает начертить градусы от 0 до 360.

Видео:11 класс, 46 урок, Теорема о биссектрисе треугольникаСкачать

Количество биссектрис в треугольнике

Но вернемся к нашей главной теме. И ответим на вопрос – сколько БИССЕКТРИС есть в треугольнике?

Ответ в общем-то логичен, и он заложен в самом названии нашей геометрической фигуры. Треугольник – три угла. А соответственно, и биссектрис в нем будет тоже три – по одной на каждую вершину.

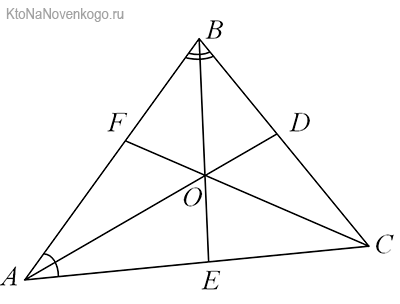
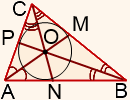
Снова посмотрим на наши рисунки. В данном случае наглядно видно, что у треугольника АВС (именно так в геометрии обозначается эта фигура – по наименованию ее вершин) три БИССЕКТРИСЫ. Это отрезки AD, BE и CF.

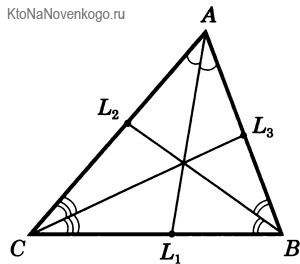
На чертежах БИССЕКТРИСЫ обозначатся следующим образом. Видите одинарные выгнутые черточки между отрезками АС /AL1 и АВ/AL1? Так обозначаются углы. А то, что они оба обозначены одинаковыми черточками, говорит о том, что углы равны. А значит, отрезок AL1 является БИССЕКТРИСОЙ.

То же самое относится и к углам между АВ/DL2 и ВС/BL2. Они обозначены одинаковыми двойными черточками. А значит, отрезок BL2 – биссектриса. А углы АС/CL3 и ВС/CL3 обозначены тройными черточками. Соответственно, это показывает, что отрезок CL3 также является биссектрисой.

Видео:Теорема о биссектрисе угла треугольника | Осторожно, спойлер! | Борис Трушин |Скачать

Пересечение биссектрис треугольника

Как можно было заметить по приведенным выше рисункам, у биссектрис треугольника есть одно важное свойство. А именно:

Биссектрисы треугольника всегда пересекаются в одной точке, называемой инцентром!

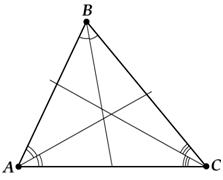
Это правило является аксиомой (что это такое?) и не допускает никаких исключений. Другими словами, вот такого быть не может:

Если вы видите такую картину, то перед вами точно не БИССЕКТРИСЫ. Во всяком случае, минимум один отрезок таковой не является. А может и все три.

А есть еще один интересный факт, связанный с пересечением биссектрис треугольника.

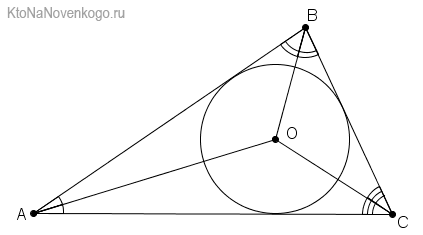
Центр пересечения биссектрис в треугольнике является центром окружности, который списан в эту фигуру.

Это свойство биссектрис на самом деле не только выглядит интересно на чертежах. Оно часто помогает в решение сложных задач.

Видео:Формула для биссектрисы треугольникаСкачать

Свойство основания биссектрисы

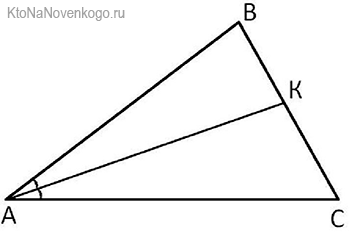
У каждой БИССЕКТРИСЫ есть основание. Так называют точку пересечения со стороной треугольника. Например, в нашем случае это будет точка К.

И с этим основанием связана одна весьма интересная теорема. Она гласит, что

Биссектриса треугольника делит противоположную сторону, то есть точкой основания, на два отрезка. И их отношение равно отношению двух прилежащих сторон.

Звучит несколько тяжеловато, но на деле выглядит весьма просто. Отношение отрезков на основании биссектрисы – это ВК/КС. А отношение прилежащих сторон – это АВ/АС. И получается, что в нашем случае теорема выглядит вот так:

Интересно, что для данной теоремы будет справедливо и другое утверждение:

Ну, как часто бывает в математике – это правило работает и в обратном направлении. То есть, если вы знаете длины все сторон и их соотношения равны, то можно сделать вывод, что перед нами БИССЕКТРИСА, А соответственно, будет проще рассчитать размер угла треугольника.

Видео:8 класс, 35 урок, Свойства биссектрисы углаСкачать

Биссектриса равнобедренного треугольника

Для начала напомним, что такое равнобедренный треугольник.

Это такой треугольник, у которого две стороны абсолютно равны (то есть имеет равные «бедра»).

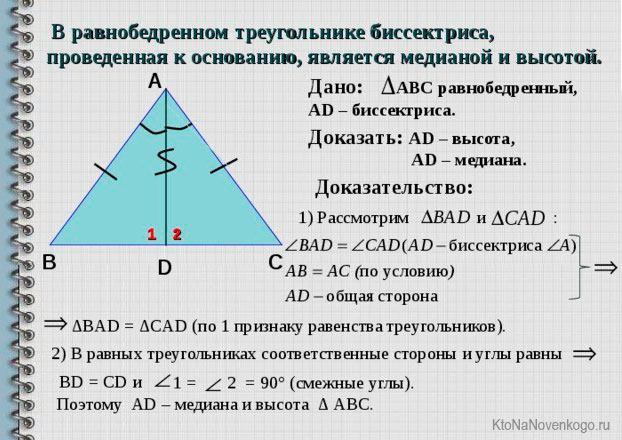
Так вот в таком треугольнике БИССЕКТРИСА имеет весьма интересные свойства.

Она одновременно является еще и медианой (что это?), и высотой.

Эти понятия нам также знакомы по школьному курсу. Но если кто забыл, мы обязательно напомним:

1. Высота – линия, которая выходит из вершины треугольника и опускается на противоположную сторону под прямым углом.
2. Медиана – линия, которая выходит из вершины треугольника, и делит противоположную сторону на две ровные части.

А в равностороннем треугольнике или как его еще называют правильном (у которого все стороны и все углы равны) все три биссектрисы являются высотами и медианами. И плюс ко всему, их длины равны.

Вот и все, что нужно знать о таком понятии, как БИССЕКТРИСА. До новых встреч на страницах нашего блога.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (3)

«Высота – линия, которая выходит из вершины треугольника и опускается на противоположную сторону под прямым углом.

Медиана – линия, которая выходит из вершины треугольника, и делит противоположную сторону на две ровные части.»

Некорректно, линия бывает разная,а речь здесь идет о прямой, или её порождениях: отрезок и луч.

Математика требует точности. Спасибо.

При ознакомлении с таким теоретическим материалом всегда возникает вопрос, как можно использовать знания о биссектрисе в реальной жизни, за пределами учебного заведения.

Необходимость делать уроки с собственным ребенком в счет не идет. Конечно, такая информация повышает общую эрудицию, но не несет никакой практической нагрузки, а потому надолго не задерживается в памяти.

Никогда не был силен в геометрии, но наука эта очень важна, знаю, потому как не раз приходилось подтягивать свои знания для решения практических задач.

Видео:Секретная формула биссектрисы треугольника плюс Задача из экзамена 9 классСкачать

Биссектриса треугольника

Биссектриса треугольника, в отличие от биссектрисы угла, является отрезком, а не лучом.

Биссектриса треугольника — это отрезок биссектрисы угла треугольника, проведенной из данной вершины, соединяющий эту вершину с точкой на противолежащей стороне.

Таким образом, биссектриса треугольника является частью биссектрисы угла треугольника (луча), которая находится внутри треугольника.

Все три биссектрисы треугольника пересекаются в одной точке.

Точка пересечения биссектрис треугольника является центром вписанной в треугольник окружности.

Свойство биссектрисы треугольника

Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные двум другим сторонам:

Более подробно о свойстве биссектрисы мы поговорим позже.

Длина биссектрисы

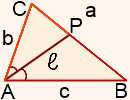
1) Длина биссектрисы треугольника через длины его сторон.

Если ввести обозначения

длина биссектрисы треугольника АВС, проведенная из вершины А, может быть найдена через длины сторон по формуле

2) Длина биссектрисы треугольника через длины сторон и пропорциональные отрезки.

Если ввести обозначения

формула длины биссектрисы примет вид:

3) Длина биссектрисы треугольника через длины сторон и угол между ними:

Если ввести обозначение ∠CAB=α, формула примет вид:

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

One Comment

Спасибо! Эта информация помогла мне при составлении доклада!

💥 Видео

Свойства биссектрисы треугольникаСкачать

Теорема о свойстве биссектрисы внешнего угла треугольника ДоказательствоСкачать

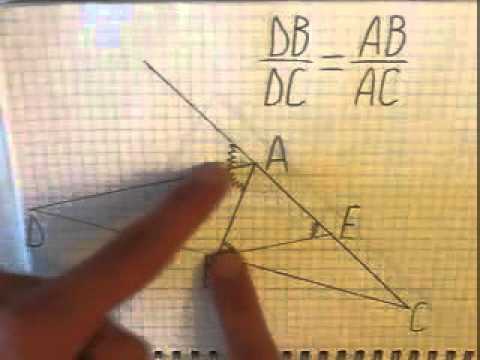
Построение биссектрисы углаСкачать

Построение биссектрисы в треугольникеСкачать

Геометрия 8 класс (Урок№29 - Свойство биссектрисы угла.)Скачать

Медиана, биссектриса и высота треугольника. Геометрия 7 класс.Скачать