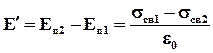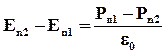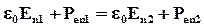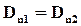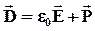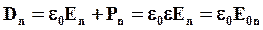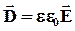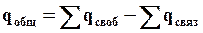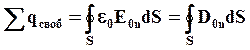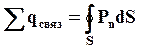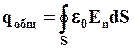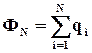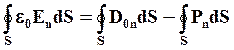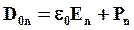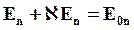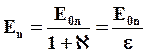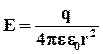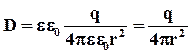Разобравшись с поведением диэлектрика на микроскопическом уровне, вернемся к плоскому конденсатору, изображенному на рис. 3.3. Откуда же взялись поляризационные заряды на поверхности диэлектрической пластины между обкладками?
Теперь мы знаем, что во внешнем поле, создаваемом обкладками, единица объема диэлектрика приобретает дипольный момент Р. Скажем, положительные заряды смещаются по направлению поля (вверх на рис. 3.3), а отрицательные — вниз. При полной однородности поля и диэлектрика объемные нескомпенсированные заряды внутри диэлектрика не появляются. Но такой сдвиг приводит к возникновению нескомпенсированных зарядов на поверхности диэлектрической пластины. Дипольный момент пластины равен VР, где V = Sd — ее объем. С другой стороны, полный поверхностный заряд на пластине равен
а расстояние между центрами положительных и отрицательных зарядов равно d (см. рис. 3.3). Поэтому дипольный момент пластины можно также записать как
Сравнивая эти два выражения, находим связь поверхностной плотности поляризационных зарядов с вектором поляризации
Напряженность Е суммарного поля внутри диэлектрика меньше напряженности поля E0, создаваемого обкладками. Именно поле Е действует на молекулы диэлектрика, именно его они «чувствуют», и потому для него справедливо соотношение (3.22)
Используя связь (3.3) напряженности поля Е ‘ поляризационных зарядов с суммарным полем Е
мы находим связь между диэлектрической проницаемостью и диэлектрической восприимчивостью
В общем случае вектор поляризации Р не параллелен вектору напряженности суммарного поля Е: в анизотропных диэлектриках вектор поляризации может поворачиваться относительно напряженности поля. Однако всегда мы можем записать соотношение
называется вектором электрического смещения (вектором электрической индукции).
В частном случае линейной зависимости поляризации от напряженности поля
вектор электрического смещения равен
где 
имеет место для изотропных диэлектриков. В общем случае вектор D не параллелен Е. Поле вектора D можно графически изобразить линиями электрического смещения, которые определяются так же, как и линии напряженности электрического поля (рис 3.23 и 3.24).
Рис. 3.23. Условия на плоской границе двух диэлектриков для напряженности и электрического смещения
Рис. 3.24. Линии напряженности и электрического смещения электрического поля
от точечного заряда, расположенного на границе раздела двух диэлектриков
В СИ единицей измерения электрического смещения является:
Видео:44. Электрическое поле в диэлектрике. Вектор поляризованностиСкачать

ВЕКТОР ЭЛЕКТРИЧЕСКОГО СМЕЩЕНИЯ ТЕОРЕМА ГАУССА ДЛЯ ПОЛЯ В ДИЭЛЕКТРИКЕ
Уменьшение напряженности электрического поля на поверхности диэлектрика происходит скачком (поскольку именно на поверхности расположены связанные заряды), что вызывает некоторые сложности при расчётах электрических полей в веществе.
Например, если пространство заполнено несколькими слоями разных диэлектриков, то даже в самой простой ситуации расчёт будет довольно сложным, так как из-за связанных зарядов в каждом слое будет своя напряжённость электрического поля.
Поэтому необходима такая характеристика электрического поля, которая нс зависит от связанных зарядов. Чтобы получить такую характеристику, поступим следующим образом.
Как уже отмечалось, напряжённость поля внутри диэлектрика Е = Eq — Е где Е’ — напряжённость поля связанных зарядов, равная ст’/?0.
Напряжённость внешнего электрического поля, созданного свободными зарядами двух параллельных бесконечных проводящих плоскостей, можно выразить как Е0 = асвоб / 80 .
Тогда напряжённость электрического поля внутри диэлектрика
Таким образом, величина е0Е + Р не зависит от связанных зарядов. Эту величину называют электрическим смещением.
Определение электрического смещения можно записать в векторной форме D = в()Е + Р , или, поскольку Р = ке0? , D = б0Е(1 + к) =
Вектор электрического смещения в изотропных диэлектриках совпадает по направлению с вектором напряжённости электрического поля внутри диэлектрика, так как в изотропных диэлектриках диэлектрическая проницаемость s является скалярной величиной [1] .
В СИ вектор электрического смещения измеряется в кулон на квадратный метр (Кл/м 2 ).
Электрическое смещение является вспомогательной характеристикой электрического поля, зависящей только от свободных зарядов.
Таким образом, получена характеристика электрического поля, не зависящая от связанных зарядов. Использование такой характеристики даёт очевидные преимущества. Действительно, используя электрическое смещение, можно рассчитать электрическое поле (значение вектора D) как внутри диэлектрика, так и вне его, учитывая только свободные заряды. После этого легко найти напряжённость электрического поля в любой точке, просто поделив значение D в этой точке на значение диэлектрической проницаемости е в этой точке и на электрическую постоянную 80.
Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Вектор электрического смещения. Граница двух диэлектриков
Источником электростатического поля являются свободные и связанные электрические заряды: линии напряженности начинаются на положительных зарядах (или в бесконечности) и оканчиваются на отрицательных (или в бесконечности).
Однако при решении задач, связанных с электрическим полем в диэлектрике, в ряде случае оказывается более удобным учитывать только поле свободных зарядов. Для этого вводится понятие вектора электрического смещения ( 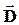
Рассмотрим изменение электрического поля на достаточно протяженной границе двух однородных и однородно поляризованных диэлектриков 1 и 2.
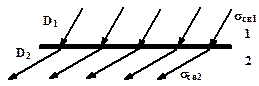 | В первом диэлектрике напряженность электрического поля и вектор поляризации соответственно равны 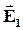 и и 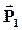 , во втором диэлектрике — , во втором диэлектрике — 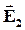 и и 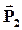 . . |
В общем случае все эти четыре вектора произвольно ориентированы в диэлектриках, поэтому можно говорить об их тангенциальных к границе раздела (Et1, Et2 и Pt1, Pt2) и нормальных (En1, En2 и Pn1, Pn2) составляющих.
На границе возникнут связанные электрические заряды противоположных знаков, поверхностные плотности которых равны sсв1 и sсв2. Эти заряды создадут электрическое полеE’. Напряженность E’ уменьшит нормальную составляющую напряженности в одном диэлектрике и увеличит в другом, поэтому E’будет определятьсяразностью нормальных составляющих напряженности:
Это уравнение можно записать так:
Отсюда видно, что на границе двух диэлектриков сохраняется нормальная составляющая:
Это и есть вектор электрического смещения.
Т.е. можно говорить о линиях электрического смещения и о потоке вектора электрического смещения через некоторую поверхность.
Поток вектора электрического смещения не изменятся на границе двух диэлектриков, т.е. линии этого вектора не начинаются и не заканчиваются на связанных зарядах, а линии напряженности поля начинаются и заканчиваются на связанных зарядах.
Из приведенных соотношений видно,
Внутри диэлектрика 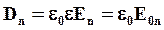
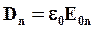
Видно, что величина Dn остается постоянной при переходе из вакуума в среду, а величина En изменяется.
Или в векторной форме:
Запишем для нашего случая теорему Гаусса. Общий заряд в диэлектрике qобщ можно найти как разность свободных зарядов и связанных зарядов.
Сумма 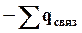
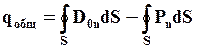
отсюда получаем:
Величина поля внутри диэлектрика:
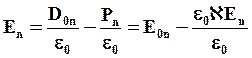
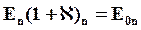
В других конкретных случаях соотношения для электростатического поля с диэлектриком имеют другой вид и чаще всего значительно более сложный, нежели полученные нами для плоской пластины внутри конденсатора. В частности, в некоторых случаях введение диэлектрика сопровождается не только ослаблением поля, но и его усилением.
 | Поле, созданное зарядом q в т. A и B, по направлению совпадает с полем связанных зарядов диэлектрика M, внесенного в поле заряда q. |
В т. C величины E0 и E’ направлены в противоположные стороны, т.е. в этой точке внесение диэлектрика сопровождается ослаблением поля.
Напряженность электрического поля точечного заряда q в диэлектрике выражается формулой:
Получаем выражение для электрического смещения поля точечного заряда:
Как видно, электрическое смещение в однородном изотропном диэлектрике не зависит от свойств вещества.
📽️ Видео
45. Электрическое смещениеСкачать

Билет №02 "Теорема Гаусса"Скачать

Билет №06-08 "Диэлектрики"Скачать

Урок 228. Диэлектрики в электрическом поле. Диэлектрическая проницаемостьСкачать

Лекция 237. Вектор электрической индукцииСкачать

ЭП в веществе 3 Вектор эл смещения СегнетоэлектрикиСкачать

Диэлектрики в электростатическом поле. Поляризация диэлектриков | Физика 10 класс #48 | ИнфоурокСкачать

Лекция №4 "Диэлектрики, вектор электрической индукции"Скачать

Диэлектрики в электрическом полеСкачать

Урок 383. Вихревое электрическое поле. Ток смещенияСкачать

Диэлектрик в электрическом полеСкачать

1.1 Векторы напряженности и индукции электрического и магнитного полейСкачать

Кокшаров Ю. А. - Электромагнетизм - Диэлектрики в электростатическом полеСкачать

Лекция 4-5 Доказательство теоремы Гаусса для вектора поляризацииСкачать

Электрическое поле. Напряженность электрического поля. Силовые линии электрического поля. 10 класс.Скачать

Лекция 4-2. Условия на границе раздела двух диэлектриковСкачать

Лекция 4 -1 Поляризация диэлектриковСкачать

1.2 Материальные уравнения, векторы поляризованности и намагниченности средСкачать